【文档说明】《【一隅三反】2023年高考数学一轮复习（提升版）（新高考地区专用）》3.2.1 函数的性质（一）（精讲）（提升版）（解析版）.docx，共(21)页，1.562 MB，由envi的店铺上传

转载请保留链接：https://www.doc5u.com/view-c9e78228876814a73911b9e82265903f.html

以下为本文档部分文字说明：

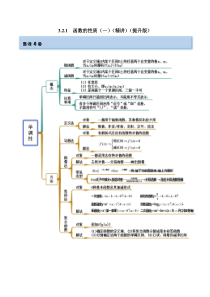
3.2.1函数的性质（一）（精讲）（提升版）思维导图考点一单调区间（无参）【例1-1】（2022·贵州）函数2()ln(231)fxxx=−+的单调递减区间为（）A．3,4−B．1,2−C．3,4+D．(1,)+【答案】B【解析】在函数2(

)ln(231)fxxx=−+中，由22310xx−+得12x或1x，则()fx的定义域为1(,)(1,)2−+，函数2231uxx=−+在1(,)2−上单调递减，在(1,)+上单调递增，又lnyu=在(0,

)u+上单调递增，于是得()fx在1(,)2−上单调递减，在(1,)+上单调递增，所以函数()fx的单调递减区间为1(,)2−.故选：B【例1-2】（2022·广东）函数()232fxxx=−+的单调递

增区间是（）A．3,2+B．31,2和)2,+C．(,1−和3,22D．3,2−和)2,+【答案】B【解析】222232,13232,1232,2xxxyxxxxxxxx−+=−+=−+−

−+如图所示：考点呈现例题剖析函数的单调递增区间是31,2和)2,+．故选：B.【例1-3】（2022·湖北）函数2()sin2cosfxxx=−−的单调递增区间是（）A．2π,(21)πkk+()kZB．ππ

2π,2π22kk−+()kZC．(21)π,2πkk−()kZD．π3π2π,2π22kk++()kZ【答案】A【解析】22()sin2coscos2cos1fxxxxx=−−=−−，设costx=，则[1,1]t−，2221(1)2yttt=

−−=−−，函数2()sin2cosfxxx=−−是由costx=和2221(1)2yttt=−−=−−复合而成，当[1,1]t−时，2221(1)2yttt=−−=−−是减函数；若求2()cos2cos1fxxx=−

−的单调递增函数，只需求costx=的单调递减区间，当[2π,(21)π]xkk+()kZ时，costx=为减函数，所以函数()fx的单调递增区间是[2π,(21)π]kk+()kZ.故选：A.【例1-4】（2022·山东·济南市历城第二中

学模拟预测）函数()53xfxxa+=−+在()1,+上是减函数，则实数a的范围是_______.【答案】(2,4]−【解析】函数5()3xfxxa+=−+，定义域为(,3)(3,)xaa−−−+，又322()133xaaafxxaxa−++++==+

−+−+，因为函数5()3xfxxa+=−+在(1,)+上是减函数，所以只需23ayxa+=−+在(1,)+上是减函数，因此2031aa+−，解得24a−.故答案为：24a−【例1-5】（20

21·云南昆明市）函数lnexy=的单调增区间是【答案】(0,)+【解析】要使函数lnxye=有意义则0x，即函数定义域为(0,)+，又lnxyex==，由一次函数的单调性可知函数lnxye=在(0,)+上

单调递增.【一隅三反】1．（2022·全国·高三专题练习）函数222xxy−++=的单调递增区间是（）A．1,2−B．(,1]−−C．112−，D．12−，【答案】C【解析】令220xx−++，解得12x−

，令22txx=−++，则yt=，∵函数22txx=−++在区间112−，上单调递增，在区间122，上单调递减，yt=在定义域内递增，∴根据复合函数的单调性可知，函数222xxy−++=的单调递增区间

是112−，．故选：C2．（2022·福建）函数()2fxxx=−的单调减区间是（）A．1,2B．1,0−C．0,2D．[2,)+【答案】A【解析】()(2),2,(2),2,xxxfxxxx−=−

直接通过解析式，结合二次函数图象得：(,1),(2,)−+递增，在1,2递减，故选：A.3．（2021·全国·高三阶段练习（文））下列函数在(),1−−上是减函数的为（）A．()lnfxx=−B．()11fxx=−+C．()234fxxx=−−D．()21fxx=【答案】C【解

析】对于选项A，()lnfxx=−在(),1−−上无意义，不符合题意；对于选项B，()11fxx=−+在(),1−−上是增函数，不符合题意；对于选项C，2234,?4134,?14xxxxxxx−−−−++−或的大致图

象如图所示中，由图可知()fx在(),1−−上是减函数，符合题意；对于选项D，()21fxx=在(),1−−上是增函数，不符合题意.故选：C.4．（2022·全国·高三专题练习）函数()lg2cos3yx=−的单调递增区间为

（）A．()()2,22kkkZ++B．()11226kkkZ++，C．()2,26kkkZ−D．()2,26kkkZ+【答案】C【解析】根据题意，2cos30x−，解得，ππ2π2,66kx

kkZ−+又函数ylgx=在定义域内为单调增函数，且函数2cos3yx=−在π2,2,6kkkZ−内为单调增函数根据复合函数的单调性可知：()2cos3ylgx=−的单调增区间为π2,2π,6kkkZ−选项C正确，选项ABD错误.故选：C.5．（2021

·天津静海区）函数()3ln2fxxxx=−的单调减区间为___________【答案】()0,e【解析】()31'ln1ln22fxxx=+−=−,当()'0fx,即1ln002xxe−时原函数为减函数.故函数()3ln2fxxxx

=−的单调减区间为()0,e.故答案为：()0,e考点二已知单调性求参数【例2-1】（2022·陕西·武功县普集高级中学）已知函数()321132afxxxx=+++在(),0−，()3,+上单调递增，在

()1,2上单调递减，则实数a的取值范围为（）A．105,32−−B．(,2−−C．10,23−−D．105,32−−【答案】A【解析】由()321132afx

xxx=+++，得()21fxxax=++．因为()fx在(),0−，()3,+上单调递增，在()1,2上单调递减，所以方程()0fx=的两个根分别位于区间0,1和2,3上，所以(0)0(1)0(2)0(3)

0ffff，即10,110,4210,9310,aaa++++++解得10532a−−.故选：A．【例2-2】（2022·河南濮阳·一模）“1b”是“函数()()22,0log2,20bxxfxxbx+=

++−是在()2,−+上的单调函数”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件【答案】B【解析】依题意，函数()fx是在()2,−+上的单调函数，由于()2log2yx

b=++在(2,0−上递增，所以()fx在()2,−+上递增，所以0b且12b+，即01b.所以“1b”是“函数()()22,0log2,20bxxfxxbx+=++−是在()2,−+上的单调函数”的必要不

充分条件.故选:B【例2-3】（2022·全国·高三专题练习）若函数()()3logafxxax=−（0a且1a）在区间1,02−内单调递增，则a的取值范围是（）A．1,14B．3,14

C．9,4+D．91,4【答案】B【解析】函数3()log()(0,1)afxxaxaa=−在区间1(,0)2−内有意义，则311()0,22a−+…14a…，设3,txax=−则logayt=，

23txa=−(1)当1a时，logayt=是增函数，要使函数3()log()(0,1)afxxaxaa=−在区间1(,0)2−内单调递增，需使3txax=−在区间1(,0)2−内内单调递增，则需使230txa=−，对任意1(0)2x−

恒成立,即23ax对任意1(,0)2x−恒成立；因为1(,0)2x−时，23034x所以0a与14a矛盾，此时不成立.(2)当01a时，1ayogt=是减函数，要使函数()()3)0,1(afxlogxaxaa=−在区间1(,0)

2−内单调递增，需使3txax=−在区间1(,0)2−内内单调递减，则需使230txa=−对任意1(,0)2x−恒成立，即23ax对任意1(,0)2x−恒成立，因为213(,0),0342xx−时，所以34a…，又1a，所以314a„.

综上，a的取值范围是314a„故选：B【一隅三反】1．（2022·全国·高三专题练习）若函数21,1()2,,1axxfxxaxx−=−是R上的单调函数，则a的取值范围（）A．20,3B．20,3C．(0,1D．()0,1【答案】B【

解析】因为分段函数()fx在R上的单调函数，由于22yxax=−开口向上，故在1x上单调递增，故分段函数()fx在在R上的单调递增，所以要满足：0212112aaaa−−−−，解得：203a故选：B2．（2021·全国·高三专题练习）已知函数()()20xfx

axa=−在()1,2上单调递减，则实数a的取值范围是（）A．1a或2aB．2aC．2a或1a=D．1a【答案】C【解析】由题意，0xa−在()1,2恒成立，则()1,2a，又()22222()2()()xxaxxaxfxxaxa−−

−==−−，∴()0fx在()1,2恒成立，∴220xax−即2xa在()1,2恒成立，∴1a，综上，2a或1a=.故选：C.3．（2022·重庆）已知函数22()42afxxxx=−−−在区间(),2−−，()3,+?

上都单调递增，则实数a的取值范围是（）A．023aB．04aC．043aD．083a已知函数的单调性确定参数的值或范围要注意以下几点：（1）若函数在区间[a,b]上单调，则该函数在此区间的任意子区间上也是单调的；（2）分段函数的单调性，除注意各段的单调性外，还要注意衔接

点的取值；（3）复合函数的单调性，不仅要注意内外函数单调性对应关系，而且要注意内外函数对应自变量取值范温馨提示【答案】D【解析】设2()42agxxx=−−，其判别式21604a=+，∴函数()gx一定有两个零点，设()gx的两个零点为1x，

2x且12xx，由2402axx−−=，得2116242aax−+=，2216242aax++=，∴121224,2()24,24,2axxxafxxxxxxaxxx+=−−+，

①当0a时，()fx在()1,x−上单调递减或为常函数，从而()fx在(),2−−不可能单调递增，故0a；②当0a时，()20ga−=，故12x−，则120x−，∵()fx在()1,x−上单调递增，∴()fx在(),2−

−上也单调递增，3(3)102ga=−−，23x，由()fx在2,8ax和()2,x+上都单调递增，且函数的图象是连续的，∴()fx在,8a+上单调递增，欲使()fx在()3,+?上单调递增，只需38a，得83a，综上：实数a的范围是

083a.故选：D.4．（2021·重庆市）已知0a且1a，若函数2()log()afxaxx=−在3,4上是减函数，则a的取值范围是__________【答案】1(,1)3【解析】令()2gxaxx=−，当1a时，

因为函数2()log()afxaxx=−在3,4上是减函数，所以函数()2gxaxx=−在3,4上是减函数，且()0gx成立，则()14241640aga=−，无解，当01a时，因为函数2()log()afxaxx=−在3,4上是减

函数，所以函数()2gxaxx=−在3,4上是增函数，且()0gx成立，则()1323930aga=−，解得113a，综上：实数a的取值范围是1(,1)3故答案为：1(,1)3考点三奇偶性的判断【例3】（2022·广西）下列函数中，既是奇函数，又在定

义域上单调递增的是（）A．cosyx=B．21xyx=+C．lnyx=D．22xxy−=−【答案】D【解析】∵函数cosyx=为偶函数，A错，∵()lnln||()fxxxfx−=−==，∴函数lnyx=为偶函数，C错，∵2()()()1xfx

fxx−−==−−+，∴函数21xyx=+为奇函数，∵当1x=时，12y=，2x=时，25y=，∴函数21xyx=+在定义域上不是单调递增函数，B错，∵()22()xxfxfx−−=−=−，又函数2xy=在定义域上单调递增，函数

2xy−=在定义域上单调递减，∴函数22xxy−=−既是奇函数，又在定义域上单调递增，D对，故选：D.【一隅三反】1．（2022·广东广州·二模）下列函数中，既是偶函数又在()0,+上单调递增的是（）A．12xy=

B．2yxx=−C．1yx=−D．1yxx=−【答案】C【解析】对A：容易知12xy=是偶函数，且在()0,+单调递减，故错误；对B：容易知2yxx=−是偶函数，当0x时，2yxx=−，其在10,2

单调递增，在1,2+单调递减，故错误；对C：容易知1yx=−是偶函数，当0x时，1yx=−是单调增函数，故正确；对D：容易知1yxx=−是奇函数，故错误；故选：C.2．（2022·河南）下列函数中，即是奇函数又是单调函数的是（）A．sinyxx=B．siny

xx=+C．tanyxx=D．tanyxx=+【答案】B【解析】因为yx=，tanyx=，sinyx=均为定义域上的奇函数，对于A：sinyxx=是偶函数，所以A错误；对于B：sinyxx=+是奇函数，且1cos0yx=+，为单调递增函数，所以B正确；对于C：tanyxx=是偶函数，所以C

错误；对于D：tanyxx=+是奇函数，但不是单调函数，所以D错误故选：B．3．（2022·安徽）设函数()fx,()gx的定义域为R，且()fx是奇函数，()gx是偶函数，则下列结论中正确的是（）A．()()fxgx是偶函

数B．|()|()fxgx是奇函数C．()()fxgx是奇函数D．()()fxgx是奇函数【答案】C【解析】()fx是奇函数，()gx是偶函数，()()()(),fxfxgxgx−=−−=，对于A，()()()(

)fxgxgxgx−−=−，故()()fxgx是奇函数，故A错误；对于B，|()|()|()|()|()|()fxgxfxgxfxgx−−=−=，故|()|()fxgx是偶函数，故B错误；对于C，()()()()fxgxfxgx−−=−，故()()fxgx是奇函数

，故C正确；对于D，()()()()fxgxfxgx−−=，故()()fxgx是偶函数，故D错误.故选：C.考点四奇偶性的应用【例4-1】（2021·河南）已知()fx为奇函数，当0x时，()24xfxxm=−+，则当0x时，()fx=（）A．241xx−−+B．241xx−−

−−C．241xx−−+−D．241xx−−++【答案】C【解析】因为()fx为奇函数，所以()010fm=−=，即1m=．当0x时，0x−，()()()224141xxfxfxxx−−=−−=−−−+=−+−．故选：C【例4-2】（202

2·河南洛阳）若函数()()322xxxafx−=−是偶函数，则=a（）A．-1B．0C．1D．【答案】C【解析】由已知，()()322xxxafx−=−，所以()()3()22xxfxax−=−−−，函数()fx为偶函数，所以()()fxfx=−，所以()()33

22()22xxxxxaxa−−−=−−，整理得：3(1)(22)0xxax−−−=，所以1a=.故选：C.【一隅三反】1．（2022·全国·高三专题练习）已知函数()11exmfxx=+−是偶函数，则m

的值是（）A．2−B．1−C．1D．2【答案】A【解析】函数的定义域为0xx，因为函数()11exmfxx=+−是偶函数，所以(1)(1)ff−=，所以11111e1emm−−

+=+−−，e11e11emm−−=+−−，所以(e1)21em−=−，得2m=−，故选：A2．（2022·江西）若函数()()11333cos22xxfxax+−−=−+为偶函数，则实数=a（）A．9−B．3C．3−D．9【答案】D【解析】由题意，函

数()()11133sin233sin293xxxxafxaxx+−−=−=−为偶函数，因为函数3sin2yx=为奇函数，所以()339xxagx−=−为奇函数，由()0009033ag−

==，可得19a=，解得9a=.故选：D.3．（2022·全国·高三专题练习）已知函数()()()()sin0cos,(0)xaxfxxbx+=+„是偶函数，则a，b的值可能是（）A．3a=，3b=B．23a=，6b=C．3a=，

6b=D．23a=，56b=【答案】C【解析】根据题意，设0x，则0x−，则()()sinfxxa=+，()()cosfxxb−=−+，又由()fx为偶函数，则()()fxfx=−，即()()sincosxaxb+=−+，变形可

得：()sinsin2xaxb+=+−对于任意x恒成立，则有22abkkZ+=+，，分析选项：C满足2ab+=，故选：C．4．（2021·河北）已知函数()fx是R上的奇函数，当0x时，()22fxxx

=−，则函数的解析式为()fx=______．【答案】222,02,0xxxxxx−−−【解析】因为函数()fx是R上的奇函数，所以()00f=，又当0x时，()22fxxx=−，设0x，则0x−，则()22fxxx−=+，因为()fx为奇函数，

所以()()fxfx−=−，所以()22fxxx=−−，所以()222,00,02,0xxxfxxxxx−==−−故答案为：222,02,0xxxxxx−−−考点五单调性与奇偶性应用之比较大小【例5-1】（2022·安徽·寿县第一中学）

若()fx为定义在R上的偶函数，且在(),0−上单调递减，则（）A．11321(ln)(2)(3)2fffB．11321(3)(ln)(2)2fffC．11321(2)(3)(ln)2fffD．11321(3)(2)(ln)2fff【答案】D

【解析】由()fx为偶函数且在(),0−上单调递减知：()fx在()0,+上单调递增，1(ln)(ln2)(ln2)2fff=−=，又ln2lne1=，113221,31，66113232228339====，

故113232ln2，所以11321(3)(2)(ln)2fff.故选：D.【例5-2】（2022·重庆·西南大学附中模拟预测）设ln2a=，ln33b=，22ec=，则a，b，c的大小关系是（）A．cabB．abcC．bcaD．bac【答案】A【

解析】因为ln2ln4ln224a===，2222lneeec==，ln33b=，所以，令()ln,0xgxxx=，()'21lnxgxx−=，所以当()e,x+时，()'0gx，函数()ln,0xgxxx=单调减，因为234e

，所以22ln3ln4lne34ebac===，即cab.故选：A【一隅三反】1．（2022·天津河北·二模）已知()fx是定义在R上的偶函数，且在区间[0,)+单递调减，若2(log6.1)af=−

，0.7(2)bf=，(3)cf=，则a，b，c的大小关系为（）A．abcB．bcaC．cbaD．bac【答案】D【解析】由函数()fx是定义在R上的偶函数，可得()()fxfx−=，则()()22log6.1log6.1aff=−=，()0.7

2bf=，()3cf=，因为函数()fx在区间[0,)+上单调递减，且2222loglog6.1log834==，00.7122212==，即20.72log6.13，所以()()()720.2log6.13fff，即有bac，故选：D．2．（2022·安

徽·巢湖市第一中学高三期中（理））已知函数()()2log41xfxx=+−，设1ln3af=，()lg5bf=，()6log3cf=，则a，b，c的大小关系为（）A．cbaB．bcaC．acbD．ab

c【答案】A【解析】因为函数定义域为()−+，22214()log()log(41)log44xxxxfxxx+−=+=+−+22log(4)2log(41)()xxxxxxfx=+−+=+−=，故函数()fx为偶函数，所以，1(ln)(ln3)3ff=，又因为4ln4(4

1)ln2(41)ln241()(41)ln2(41)ln241xxxxxxxfx−+−−===+++，当,()0x+，()0fx，()fx单调递增，当(,0)x−，()0fx，()fx单

调递减，所以，,()0x+时，比较6ln3,lg5,log3之间的大小，得到ln31，且61lg50,1log30，所以，再比较lg5和6log3的大小，因为10lg5lg()1lg22==−，666

6log3log()1log22==−，明显可见，6lg2log266lg51lg21log2log3=−−=，得到6ln3lg5log3，根据()fx的单调性，可得()()()61lnln3lg5log33ffff

=abc故选:A3．（2022·云南德宏））已知函数()fx是定义在R上的偶函数，对任意1x，2(0,)x+，都有121212()()0()fxfxxxxx−−，131(log)2af=，21(log)3bf=，12(5)cf=，则（）A．

abcB．cabC．bacD．cba【答案】D【解析】因为对任意1x，2(0,)x+，都有121212()()0()fxfxxxxx−−，所以()fx在(0,)+上单调递增，又函数()fx

是定义在R上的偶函数，所以()()fxfx=−因为1331loglog22=，又3330log1log2log31==所以()131log0,12，又2221log2log3log42==，12552=所以1221310loglog325，所

以()()22211321log3log3log5o3lg12fffff=−=所以cba.故选：D.4．（2022·湖北·荆门市龙泉中学一模）设3103a=，ln1.03b=，0.03e1=−c，则下列

关系正确的是（）A．abcB．bacC．cbaD．cab【答案】C【解析】记()()e1,0xfxxx=−−.因为()e1xfx=−，所以当0x时，()0fx，所以()fx在()0,+上单调递增函数，所以当0x时，()()00fxf=

，即1xex−，所以0.03e10.03−.记()()()ln1,0gxxxx=+−.因为()11011xgxxx−=−=++，所以()gx在()0,+上单调递增函数，所以当0x时，()()00gxg=，即()ln1xx+，所以ln1

.030.03.所以cb.记()()()ln1,01xhxxxx=+−+.因为()()()2211111xhxxxx=−=+++，所以当0x时，()0hx，所以()hx在()0,+上单调递

增函数，所以当0x时，()()00hxh=，即()ln11xxx++，所以0.033ln1.0310.03103=+.所以ba.综上所述：cba.故选：C考点六单调性与奇偶性应用之解不等式【例6-1】（2022·安徽马鞍山）已知偶函数()fx在(,0−上单调递

增，且()20f=，则不等式()10xfx−的解集为（）A．()(),10,3−−B．()()103−+,,C．()1,3−D．()()2,02,−+【答案】B【解析】偶函数()fx在(,0−上单

调递增，则()fx在(0,)+上单调递减，而()20f=，因()10xfx−，则当0x时，(1)0(|1|)(2)fxfxf−−，即|1|2x−，解得3x，当0x时，(1)0(|1|)(2)fxfxf−−，即|1|2x−，解得10x−，所以不等式()10xfx−的解

集为()()103−+,,.故选：B【例6-2】（2022·安徽·）已知()()2log91afxxax=+−是奇函数，若()()20faxbxfaxa+++恒成立，则实数b的取值范围是（）A．

()3,3−B．()9,3−C．()3,9−D．()9,9−【答案】B【解析】()fx是奇函数，()()()()0fxfxfxfx−=−+−=恒成立，即()()()()22log91log910aaxaxxax+−+−+−−

=恒成立，化简得，()222log910axax+−=，即()2222291190xaxax+−=−=，则290a−=，解得3a=，又0a且1a，3a=，则()()23log913fxxx=+−，所以()()2332

1log913log913fxxxxx=+−=++，由复合函数的单调性判断得，函数()fx在)0,+上单调递减，又()fx为奇函数，所以()fx在R上单调递减；由()()20faxbxfaxa+++恒成立得，()()()()22333

333fxbxfxfxbxfx+−++−−恒成立，则()223333330xbxxxbx+−−+++恒成立，所以()234330b=+−恒成立，解得93b−.故选：B.【一隅三反】1．（2022·云南昭通）若定义在R上的奇函数()f

x在(0,)+上单调递增，且(2)0f=，则不等式(1)0xfx+的解集为（）A．(,3][1,)−−+B．(,3][0,1]−−C．3,1][,[01]−−D．[3,1][1,)−−+【答案】C(1)0xfx+0,

(1)0xfx+或0,(1)0,xfx+又()fx在(0,)+上单调递增，且(2)0f=0,0,01(1)0012xxxfxx++()fx在R上为奇函数()fx在(,0)−上单调递增，且(2)0f−=0,0,31(1)0210xx

xfxx−−+−+综上：不等式(1)0xfx+的解集为3,1][,[01]−−故选：C.2．（2022·河南）已知定义在R上的函数()()()1fxxxa=−+为奇函数，则不等式()10

2xfx−的解集为（）A．()()1,00,1−UB．11,0,122−C．()11,00,2−D．()11,0,12−【答案】D【解析】因为()fx是定义在R上的奇函数，所以()00fa=−

=，即0a=.所以()()1fxxx=−，化简得()22,0,,0xxxfxxxx−=−−．因为()102xfx−，所以()1,20xfx或()1,20xfx．解得112x或10x−.故选：D3．（202

2·全国·高三开学考试（理））已知()fx是定义在(26,)aa−上的奇函数，且()fx在)0,a上单调递减，则不等式()()3114fxfx−−的解集为（）A．12,37−B．23,74

C．2,17D．12,47−【答案】B【解析】因为()fx是定义在(26,)aa−上的奇函数所以260aa−+=，得：2a=又()fx在)0,2上单调递减所以()fx在()2,2−上单调递减由()()3114fxfx−−可得：231221423114x

xxx−−−−−−，解得：23,74x所以不等式()()3114fxfx−−的解集为：23,74.故选：B.4．（2022·贵州遵义）若奇函数()fx在()0,+单调递增，且()10f=，则满足()02fxx−的x的取值

范围是（）A．()(),10,1−−B．()()1,02,−+C．()()1,01,−+D．()()1,01,2−【答案】D【解析】由()fx是奇函数在()0,+单调递增，且()10f=可知：当(

)()101,x−+，时，()0fx，当()()101x−−，，时，()0fx，又()()00220fxfxxx−−或()020fxx−，解得：10x−或12x满足()02fxx−的x的取值范围是10x−

或12x故选：D5．（2022·全国·高三专题练习）已知函数2e()1lnxfxx=+，则不等式()exfx的解集为（）A．()0,1B．1,1eC．()1,eD．()1,+【答案】B【解析函数2e()1lnxfxx=+，则21ln

eee()ee1ln1lnxxxxxfxxxx+++，因0x，则不等式()exfx成立必有1ln0x+，即1ex，令,(e)e1xxgxx=，求导得2e(1)()−=xxgxx，当11ex时，()0gx

，当1x时，()0gx，因此，函数()gx在1(,1)e上单调递减，在(1,)+上单调递增，又()e(1ln)()xfxgxgx+，当1x时，ln11x+，于是得1lnxx+，即1ln0xx+−，

令()1lnhxxx=+−，当1x时，1()10hxx=−，函数()hx在(1,)+上单调递减，1x，()(1)0hxh=，因此，1lnxx+无解，当11ex时，0ln11x+，于是得1lnxx+，即1ln0xx+−，此时1()10hxx=−，函数()hx在1(

,1)e上单调递增，1(,1)ex，()(1)0hxh=，不等式1lnxx+解集为1(,1)e，所以不等式()exfx的解集为1(,1)e.故选：B