【文档说明】《【一隅三反】2023年高考数学一轮复习（提升版）（新高考地区专用）》1.3 复数（精讲）（提升版）（解析版）.docx，共(14)页，874.555 KB，由envi的店铺上传

转载请保留链接：https://www.doc5u.com/view-5184285d7ed27e7a50c85ec0c3be71b7.html

以下为本文档部分文字说明：

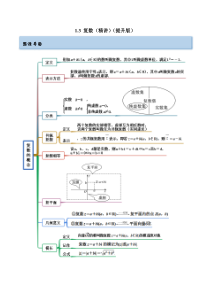
1.3复数（精讲）（提升版）思维导图考点呈现考点一复数的基本知识【例1】（2022·全国·高三专题练习）已知复数53i1iz+=−，则下列说法正确的是（）A．z的虚部为4iB．z的共轭复数为1﹣4iC．|z|＝5D．z在复平面内对应的点在第二象限【答案】B【解析】∵

()()()()53i1i53i28i14i1i1i1i2z++++====+−−+，∴z的虚部为4,z的共轭复数为1﹣4i，|z|17=，z在复平面内对应的点在第一象限.故选：B【一隅三反】1．（2022·全国·高三专题练习

）若复数3iz=−，其共轭复数为z，则（）A．z的虚部为i−B．10zz=C．z在复平面上对应的点在第四象限D．43i55zz=+【答案】D【解析】因为复数3iz=−，所以3iz=+，z的虚部为1−，(3i)(3i)86izz=−−=−，3iz=+对应点(3,1)在第一象限，286i4310

55zzizzz+===+，故选：D2．（2022·全国·高三专题练习（多选））已知复数()i,zxyxyR=+，则（）A．20z³B．22zxy=+例题剖析C．若12iz=+，则1x=，2y=D．z的虚部是iy【答案】BC【解析】()i,zxyxy

R=+，2222izxyxy=−+，故不能推出20z³，A不正确；由复数模的定义22zxy=+，故B正确；根据复数相等知，12zi=+时1x=，2y=正确，故C正确；由虚部的定义知，z的虚部是y,故D不正确.故选：BC3．（2022·浙江省

义乌中学模拟预测）已知复数(2i)(1i)za=++，其中i是虚数单位，aR，下列选项中正确的是（）A．若z是纯虚数，则这个纯虚数为5i−B．若z为实数，则2a=C．若z在复平面内对应的点在第一象限，则122aD．当2a=时，5z=

【答案】D【解析】()(2i)(1i)2+2+1izaaa=++=−，对于A：当z是纯虚数时，则20a−=且2+10a，解得2a=，此时这个纯虚数为5i，故A不正确；对于B：当z为实数时，则2+10a=，解得12a=−，故B不正确；对于C：当z在复平面内对应的点在第

一象限，则2>02+1>0aa−，解得122a−，故C不正确；对于D：当2a=时，5zi=，所以5z=，故D正确，故选：D.考点二复数的模长【例2-1】（2022·湖南·高一期中）已知复数()izmmR=+，则“10z”是“3m”的（）A．充分不必要条件B．充要条件C．必要不充分条

件D．既不充分也不必要条件【答案】C【解析】由2110zm=+，得29m，解得3m或3m−.故“10z”是“3m”的必要不充分条件.故选：C【例2-2】（2022·福建宁德·模拟预测）若()1

i6z+=，则·zz的值为（）A．2B．2C．3D．3【答案】D【解析】因为()1i1i26zzz+=+==，所以3z=，故设()i,Rzabab=+，则223ab+=，所以()()222·ii3zzabababz=+−=+==.故选：D【例2-3】（2022·全国·高三专题练习）若复

数z满足13i3z−+=，则z的最大值为（）A．1B．2C．5D．6【答案】C【解析】设i,zababR=+、.则13i3z−+=表示复平面点(,)zab到点(1,3)−的距离为3.则z的最大值为点(1,

3)−到(0,0)的距离加上3.即max1335z=++=.故选：C.【例2-4】（2022·全国·高三专题练习）若复数z满足|1||12|zii−+=−，其中i为虚数单位，则z对应的点(x，y)满足方程（）A．

22(1)(1)5xy−++=B．22(1)(1)5xy−++=C．22(1)(1)5xy++−=D．22(1)(1)5xy++−=【答案】B【解析】设(,)zxyixyR=+，代入112zii−+=−得：()()22115xy−++=

.故选：B【一隅三反】1．（2022·河南·模拟预测（理））已知复数z满足i2z−=，z为z的共轭复数，则zz的最大值为（）A．1B．4C．9D．16【答案】C【解析】设()iR,Rzxyxy=+，则

()i=ii=1izxyxy−+−+−，由i2z−=，得()2212xy+−=，即()2214xy+−=，所以z所对应的点(),xy的轨迹是以()0,1为圆心2为半径的圆，因为z为z的共轭复数，所以izxy=−即22zzxy=+，而22zzxy=+可看作该圆上的点(),xy

到原点的距离的平方，所以()()()()222max00039zz=−+−=.故选：C.2（2022·重庆·高三阶段练习）已知复数z满足i1z−=，复数z的共轭复数为z，则z的最大值为（）A．1B．2C．3D．4【答案】B【解析】令izxy

=+，,Rxy，则i1z−=表示与(0,1)距离为1的点集，即22(1)1yx+−=，此时，z表示圆()2211xy+−−=上点到原点距离，所以z的最大值，即为圆上点到原点的最大距离，而圆心到原点距离为1

，且半径为1，所以圆上点到原点的最大为2.故选：B.3．（2022·全国·高三专题练习）若z是复数，|z+2-2i|＝2，则|z+1-i|+|z|的最大值是（）A．2B．52C．222+D．324+【答案】D【解析】设z＝x+yi(x，y∈R)，由|z+2-2i|＝2知，动点

(),Pxy的轨迹可看作以()2,2C−为圆心，2为半径的圆，|z+1-i|+|z|可看作点P到()1,1A−和()0,0O的距离之和，而|CO|＝22，|CA|＝2，易知当P，A，O三点共线时，|z+1-i|+|z|取得最大值时，且最大值为|PA|+|PO|＝(|CA|+2)+(|CO|+2)＝

324+，故选：D．考点三复数的几何意义【例3-1】（2022·全国·高三专题练习）设复数z满足i1zz=−=，且在复平面内z对应的点位于第一象限，则z=（）A．13i22+B．31i22+C．34i55+D．43i55

+【答案】B【解析】把四个选项一一代入i1zz=−=验证：对于A：z=13i22+，则有1z=，()221331ii2231i1222z+−−=−=+=−.故A错误；对于B：z=31i22+，则有1z=，()2

21312321i2ii2z−=−=+=−+.故B正确；对于C：z=34i55+，则有1z=，()()2213431i55501ii55z−=−=+=−+.故C错误；对于D：z=43i55+，则有1z=，()()22143422i5555ii55z−

=−=+=−+.故D错误；故选：B【例3-2】（2022·山东潍坊·模拟预测）（多选）已知复数z满足11zz=−=，且复数z对应的点在第一象限，则下列结论正确的是（）A．复数z的虚部为3i2B．113i22z=−C．21zz=−D．

复数z的共轭复数为13i22−+【答案】BC【解析】设复数()i,Rzabab=+.因为11zz=−=，且复数z对应的点在第一象限，所以()22221110,0ababab+=−+=，

解得：1232ab==，即13i22z=+.对于A：复数z的虚部为32.故A错误；对于B：13i11322i221313ii2222z−==−+−.故B正确；对于C：因为22131313ii,

1i222222zz=+=−+−=−+，所以21zz=−.故C正确；对于D：复数z的共轭复数为13i22−.故D错误.故选：BC【一隅三反】1．（2022·全国·高三专题练习（理））已

知i是虚数单位，则复数2020202122izi−=+对应的点所在的象限是（）A．第一象限B．第二象限C．第三象限D．第四象限【答案】D【解析】20202021212222(2)(2)5iiiziiii−−−====+++−

.所以复数对应的点21(,)55−在第四象限，故选：D2．（2022·河南新乡·高二期中（理））若复数z在复平面内对应的点位于第二象限，则（）A．2z不可能为纯虚数B．2z在复平面内对应的点可能位于第二象限C．2z在复平面内对应的点一定位于第三象限D．2z在复平面内

对应的点可能位于第四象限【答案】D【解析】由z为第二象限，其对应辐角范围为,2，所以2z对应辐角为(),2，故2z在复平面内对应的点可能位于第三、四象限及y轴的负半轴.所以A、B、C错误，D正确.故选：D3．（2022·全国·高三专题练习）已知

复数z对应的点在第二象限，z为z的共轭复数，有下列关于z的四个命题：甲：2zz+=−；乙：2izz−=；丙：4zz=；丁：13i22zz=−−．如果只有一个假命题，则该命题是（）A．甲B．乙C．丙D．丁【答案】B【解析】设i,izabzab=+=−，由于z对应

点在第二象限，所以0,0ab，20zza+=，2izzb−=，22zzab=+，()()()22222222222ii2i2iiiiabzabababababababababababz++−+−====+−−++++.甲22,1aa=−=−，乙22,1bb=

=，丙224ab+=，丁222222123,322ababbaabab−=−=−=−++，由于“只有一个假命题”，所以乙是假命题，b的值应为3.故选：B考点四复数与其他知识的综合运用【例4】（2022·全国·高

三专题练习）已知i为虚数单位，则复数22019202012i3i2020i2021iz=+++++的虚部为（）A．1011−B．1010−C．1010D．1011【答案】B【解析】因为22019202012i3i2020i20

21iz=+++++，所以2320202021ii2i3i2020i2021iz=+++++，相减得20212202020211ii)1iii2021i2021i12021i(11iz−=++++−−=−−−=，所以2ii

)(1i)i2021i2021iiii)(112021(1202111011101012i)(1z+−−+====−−+−−−，虚部为1010−．故选：B．【一隅三反】1．（2022·全国·高三专题练习（理））在复平面内，复数2i，4对应的点分别为A，B.若C为线段AB上的点，且AC

CB=，则点C对应的共轭复数是（）A．12i+B．2i+C．2i−D．12i−【答案】C【解析】由题意知，复平面内点A和点B的坐标分别为()0,2A，()4,0B，设点C的坐标为(),Cxy所以()(),24,ACxyCBxy=−=

−−，，根据ACCB=得，42xxyy=−−=−计算得21xy==所以点C对应的复数为2i+，其共轭复数为2i−，选项C正确.故选：C.2．（2022·全国·高三专题练习）已知1z，2z是复数，则“12zz=”是“2121zzz=”的（

）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件【答案】A【解析】设1izab=+，(),abR,当12zz=，即2izab=−时，2221zab=+，()()2212iizzababab=+−=+所以2121zzz=取11iz=+，21

iz=−+，122zz=−,12z=,则满足2121zzz=，但显然不满足12zz=所以“12zz=”是“2121zzz=”的充分不必要条件故选：A3．（2022·河南商丘）定义函数()()()*,1nfxnxn=+N，若()i,32ifn=（i为虚

数单位），则312nxx+的展开式中系数最大项为（）A．23254xB．1431058xC．615xD．223454x【答案】C【解析】由已知()1i32in+=，两边取模，得()232n=，所以n＝10．二项式312nxx+

的展开式的通项为43131122rrnrrnrrrnnTCxCxx−−+==，因为n＝10，则4101031101031122rrrrrrrTCxCxx−−+==．令第r＋1项的系数最大，则111010111

01011221122rrrrrrrrCCCC++−−，即11012111112rrrr−+−，解得81133r，因为*rN，所以r＝3，所以33

664101152TCxx==，故系数最大的项为615x．故选：C．考点五解复数的方程【例5】（2022·全国·高三专题练习）已知方程()20xxmmR++=有两个虚根,，若3−=，则m的值是（）A．2−或52B．2−C．5

2D．52−【答案】C【解析】由已知方程有两个虚根,，因此方程判别式小于0，即.1140,4mm−,设=i,iabab+=−由韦达定理可知1m+=−=，所以2221,aabm=−+=,即214mb=+3−=,即2i3b=,所以239,24bb==所以915442m=+=

故答案为：C【一隅三反】1．（2022·重庆八中模拟预测）若虚数单位i是关于x的方程()20,xaxbabR++=的一个根，则iab−=（）A．0B．1C．2D．2【答案】B【解析】由题，i是方程的一个根，所

以2ii0ab++=，即1i0ab−++=，则i1ab+=，所以()()iiiab+−=−，即iiab−=−，所以ii1ab−=−=，选：B2．（2022·山东枣庄·一模）设1z，2z是方程210xx++=在复数范围内的两个解，则（）A．122zz−=B．12

z=C．121zz+=D．121zz=【答案】D【解析】由方程210xx++=得1430=−=−，由求根公式得213i13i22−−=，不妨设113i22z=−+，213i22z=−−.12i33zz−==，A错误；2121313i12222z=−+=−+=，

B错误；121zz+=−，C错误；2122131313iii1222222zz−+−−=−−==，D正确.故选：D.3．（2022·全国·高三专题练习）复数z满足1z=，且使得关于x的方程20

xzxz++=有实根，则这样的复数z的个数为（）A．1个B．2个C．3个D．4个【答案】C【解析】设i,,zababR=+,因为1z=,所以221ab+=,所以将i,,zababR=+代入方程20xz

xz++=整理()()2i0xaxabbx+++−=，因为关于x的方程20xzxz++=有实根，所以200xaxabbx++=−=所以当0b=时，解得1a=，此时关于x的方程为210xx++=或210xx−−=

，易知方程210xx++=无实数根，故舍去，所以1z=−；当0b时，解得1x=，12a=−，所以32b=，所以13i22z=−，此时方程有实数根1x=，满足条件.综上，13i22z=−或1z=−.故这

样的复数z的个数为3个.故选：C考点六综合运用【例6】（2022·河北·石家庄二中）（多选）下列四个命题中，真命题为（）A．若复数z满足zR，则zRB．若复数z满足1Rz，则zRC．若复数z满足2zR，则zRD．若复数1z，

2z满足12zzR，则12zz=【答案】AB【解析】对选项A，若复数zR，设za=，其中aR，则=za，zR则选项A正确；对选项B，若设1az=，其中aR，且0a，则1zRa=，则选项B正确；对选项C，若2zR，设zi=，则21zR=−

，但ziR=，则选项C错误；对选项D，若复数1z，2z满足12zzR，设1zi=，2zi=，则121zz=−R，而21ziz=−，则选项D错误.故选：AB.【一隅三反】1．（2022·全国·模拟预测）（多选）已知复数1

3i22z=−+（i为虚数单位），则下列说法中正确的是（）A．31z=B．2zz=C．230zzz++=D．220210zzz+++=【答案】AC【解析】13i22z=−+，221313ii2222zz=−+=−−

，故B错误；321313ii12222zzz==−−−+=，故A正确；231313ii102222zzz++=−+−−+=，故C正确；()6732021322zzzz==，230zz

z++=，()4563230zzzzzzz++=++=，()7896230zzzzzzz++=++=，()220212326731zzzzzzzz+++=++++=−，故D错误.故选：AC.2．（2022·福建泉州·模拟预测）（多选）设12,zz为

复数，则下列命题正确的是（）A．若120zz−=，则12zz=B．若12=zz，则2212zz=C．若120zz+，则21zz=D．若120zz=，则10z=或20z=【答案】AD【解析】对于A，设1izababR=+，，，2izcdcdR=+，，，则

()()22120zzacbd−=−+−=，00acbd−=−=，即acbd==，12zz=，A正确；对于B，令11z=，2zi=，则121zz==，此时2212zz，B错误；对于C，令11zi=+，2z

i=−，则1210zz+=，此时21zz，C错误；对于D，设1izab=+，2izcd=+，则()()12i0zzacbdadbc=−++=，00acbdadbc−=+=，即acbdadbc==−，则22acdbcd=−；若0cd==，则22acdbcd=−成立，此时20

z=；若0c=，0d，由acbd=知：0b=；由adbc=−知：0a=；此时10z=；同理可知：当0c，0d=时，10z=；若0c，0d，由22acdbcd=−得：22ab=−，0ab==，此时10z=；综上所述：

若120zz=，则10z=或20z=，D正确.故选：AD.3．（2022·山东青岛·高三期末）（多选）已知复数()21izaa=+−，i为虚数单位，aR，则下列正确的为（）A．若z是实数，则1a=−B．复平面内表示复数z的点位于一条抛

物线上C．32zD．若21zz=+，则1a=【答案】BC【解析】选项A：由复数()21izaa=+−是实数可知210a−=，解之得1a=.选项A判断错误；选项B：复数()21izaa=+−在复平面内对应点2(,1)Zaa−，其坐标满足方程21yx=−，即点2

(,1)Zaa−位于抛物线21yx=−上.判断正确；选项C：由()21izaa=+−，可得()222242213311242zaaaaa=+−=−+=−+.判断正确；选项D：21zz=+即()()221i=2121iaaaa+−+−−可得()22211

21aaaa=+−=−−，解之得1a=−.选项D判断错误.故选：BC