【文档说明】《【一隅三反】2023年高考数学一轮复习（提升版）（新高考地区专用）》1.1 集合（精讲）（提升版）（解析版）.docx，共(11)页，738.363 KB，由envi的店铺上传

转载请保留链接：https://www.doc5u.com/view-9f22fbfccefe8779df2ec1fc2a0a0b96.html

以下为本文档部分文字说明：

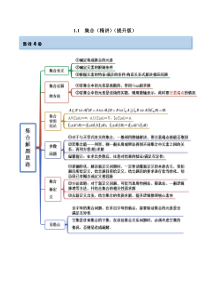
1.1集合（精讲）（提升版）思维导图考点一集合的基本运算【例1-1】（2022·江苏·苏州中学高三开学考试）已知集合A＝2|420,{|log,1}xxByyxx−==，则A∩B＝（）A．(0，2]B．(0，2)C．(1，2]D．(0，＋∞)【

答案】A【解析】∵由420x−，即222x，解得2x，所以集合(,2A=−，由当1x时，22log>log10yx==，得()0B=+，，所以(0,2AB=．故选：A.【例1-2】（2022·河北保定·高三期末）设集合,,ABC均为非

空集合.（）A．若ABBC=，则AC=B．若ABBC=，则AC=C．若ABBC=，则CBD．若ABBC=，则CB【答案】C【解析】对于A,，ABBC=，当1,2,1,1,2,3ABC===时，结论不成立，

则A错误；对于B,ABBC=，当1,2,3,1,2,3ABC===时，结论不成立，，则B错误；对于C,因为ABB，ABBC=，所以BCB，又BBC，所以BBC=，则CB,则C正确;对于D

，ABBC=，当1,1,2,1,2,3ABC===时，结论不成立,则D错误;故选:C.【例1-3】（2022·全国·高三专题练习）已知集合2(,)|0Axyaxya=+−=，22(,)|1Bxyx

y=+=，则AB的元素个数为（）A．2B．1C．0D．无法确定考点呈现例题剖析【答案】A【解析】0a=时，0y=与圆相交有两个交点0a时，24422||1211121aadaaaa−===+++∴直线与圆相交，有两个交点故选：A【一隅

三反】1．（2022·浙江绍兴·高三期末）已知全集U=R，集合Z11Axx=−，4R01xBxx−=−，则()UAB=ð（）A．1,2B．)2,4C．0,1,2D．2,1【答案】D【解析】由11x−，可得11

1x−−，即02x，则Z11Axx=−0,1,2=由401xx−−，可得4x或1x，则4R01xBxx−=−R4xx=或1x则14URBBxx==痧，故()0,1,2141,2UABxx==ð故选：D2．（2

022·全国·模拟预测）已知全集U=R，集合2,1xAyyx==，()2lg9Bxyx==−，则图中阴影部分表示的集合为（）A．[]3,2-B．()3,2−C．(3,2−D．)3,2−【答案】

B【解析】由1x，得22x，则)2,A=+，所以()U,2A=−ð.\由290−x，得33x−，则()3,3B=−，则图中阴影部分表示的集合为()U3,2BA=−ð.故选:B.3．（2022·全国·

高三专题练习）设集合{|24kMxx+==−，}kZ，{|42kNxx==+，}kZ，则（）A．MN=B．MNÜC．MND．MNÝ【答案】B【解析】{|24kMxx==+，}kZ，{|42kNxx==+，}kZ，对于集合

N，当2()kmm=Z时，22mx=+，mZ；当21()kmmZ=−时，24mx=+，mZ．MNÜ，故选：B．4．（2022·全国·高三专题练习）已知集合22(,)1Axyxy=+=，(,)Bxyyx==，则AB中元素的个数为（）A．3B．2C．1

D．0【答案】B【解析】集合中的元素为点集，由题意，可知集合A表示以()0,0为圆心，1为半径的单位圆上所有点组成的集合，集合B表示直线yx=上所有的点组成的集合，又圆221xy+=与直线yx=相交于两点22,22，22,22−−

，则AB中有2个元素.故选B.考点二集合中的参数问题【例2-1】（2022·全国·高三专题练习）集合{1Axx=−或3}x，10Bxax=+若BA，则实数a的取值范围是（）A．1,13−B．1,13−C．()),10,−−+D．()1,00,

13−【答案】A【解析】BA，①当B=时，即10ax+„无解，此时0a=，满足题意．②当B时，即10ax+„有解，当0a时，可得1xa−„，要使BA，则需要011aa−−，解得01a．当0a时，可得1xa−…，要使BA，则需要013

aa−…，解得103a−„，综上，实数a的取值范围是1,13−．故选：A．【例2-2】（2022·全国·高三专题练习）已知集合(),0Axyxaya=+−=，()(),2310Bxyaxay=++−=.若AB=，则实数=a（）A．3B．1−C．

3或1−D．3−或1【答案】A【解析】因为AB=，所以直线0xaya+−=与直线()2310axay++−=没有交点，所以直线0xaya+−=与直线()2310axay++−=互相平行，所以()1230aaa+−=，解得1a=−或3a=，当1a=−时，两直线为：10xy−+

=，10xy−+−=，此时两直线重合，不满足，当3a=时，两直线为：330xy+−=，3910xy+−=，此时两直线平行，满足，所以a的值为3，故选：A.【例2-3】（2022·全国·高三专题练习（理））设集合2230Axxx=+−，集合

2210,0,Bxxaxa=−−若AB中恰含有一个整数，则实数a的取值范围是（）A．34,43B．30,4C．3,4+D．()1,+【答案】A【解析】A={x|x＜﹣3或x＞1}，函数y=f（x）=x2﹣2ax﹣1的对称轴为x=a

＞0，而f（﹣3）=6a+8>0，f（﹣1）=2a>0，f（0）<0，故其中较小的零点为（-1，0）之间，另一个零点大于1，f（1）<0，要使A∩B恰有一个整数，即这个整数解为2，∴f（2）≤0且f（3）＞0，即44109610aa−−−−，解得：

3443aa，即34≤a＜43，则a的取值范围为34,43．故答案为：A.【一隅三反】1．（2022·全国·高三专题练习（理））设集合11Axx=−，20Bxxa=−+，若ABB=，则a的取值范围为（）A．(

),0−B．(,0−C．()2,+D．)2,+【答案】A【解析】11=02Axxxx=−，2aBxx=，由ABB=得AB，所以0a.故选：A.2．（2022·全国·高三专题练习）已知集合2

230AxNxx=−−，20Bxax=+=，若ABB=，则实数a的取值集合为（）A．1,2−−B．1,0−C．{}2,0,1-D．2,1,0−−【答案】D【解析】22301,2AxNxx=−−=，因为ABB=，所以BA，当0a

=时，集合20Bxax=+==，满足BA；当0a时，集合220Bxaxxa=+===−，由BA，1,2A=得21a−=或22a−=，解得2a=−或1a=−，综上，实数a的取值集合为2,1,0−−.故选：D.3．（2022·全国·高

三专题练习）已知集合(),30Axyxy=−=，(),10Bxyxmy=++=.若AB=，则实数m=（）A．-3B．13−C．13D．3【答案】B【解析】因为AB=，所以直线30xy−=与直线10xmy++=平行，

所以3(1)10m−−=所以13m=−.经检验，当13m=−时，两直线平行.故选：B.4．（2022·全国·高三专题练习（理））已知A={-1，2}，B={x|mx+1=0}，若A∪B=A，则实数m的取值所成的集合是（）A．11?2，−B．112−，C．1?102

−，，D．1012−，，【答案】D【解析】∵A∪B=A,∴B⊆A,∴B=∅,{−1}或{2}.m=0时，B=∅，满足条件．m≠0时，−m+1=0，或2m+1=0，解得m=1或−12.综上可得：实数m的取值所成的集合是

1,0,12−.本题选择D选项.考点三集合中的新定义【例3】（2022·全国·高三专题练习）（多选）对任意A，BR，记{|}ABxxABxAB=，，则称AB为集合A，B的对称差．例如，若123A=，，，2

34B=，，，则14AB=，，下列命题中，为真命题的是（）A．若A，BR且ABB=，则A=B．若A，BR且AB=，则AB=C．若A，BR且ABA，则ABD．存在A，BR，使得RRABAB=痧【答案】A

BD【解析】对于A选项，因为ABB=，所以{|}BxxABxAB=，，所以AB，且B中的元素不能出现在AB中，因此A=，即选项A正确；对于B选项，因为AB=，所以{|}xxABxAB=

，，即AB与AB是相同的，所以AB=，即选项B正确；对于C选项，因为ABA，所以{|}xxABxABA，，所以BA，即选项C错误；对于D选项，AB=时，AB=，()()RRABAB==痧，D正确；故选：ABD．【一隅

三反】1．（2022·贵州）定义集合|ABxxA−=且xB.己知集合Z26Uxx=−，0,2,4,5A=，1,0,3B=−，则()UAB−ð中元素的个数为（）A．3B．4C．5D．6【答案】B

【解析】因为0,2,4,5A=，1,0,3B=−，所以2,4,5AB−=，又因为1,0,1,2,3,4,5U=−，所以()U1,0,1,3AB−=−ð.故选：B.2．（2022·湖南·雅礼中学一模

）已知集合22(,)|1,,AxyxyxyZ=+，(,)|2,2,,BxyxyxyZ=，定义集合12121122(,)|(,),(,)ABxxyyxyAxyB=++，则AB中元素的个数为A．77B．49C．45D．30【答案】C【解析】因为集合，所以集合中有5个元素（

即5个点），即图中圆中的整点，集合中有25个元素（即25个点）：即图中正方形中的整点，集合的元素可看作正方形中的整点（除去四个顶点），即个．3．（2022·全国·高三专题练习）若一个集合是另一个集合的子集，则称两个集合构成“鲸吞”；若两个集

合有公共元素，且互不为对方子集，则称两个集合构成“蚕食”，对于集合{}1,2A=-，22,0Bxaxa==，若这两个集合构成“鲸吞”或“蚕食”，则a的取值集合为_____.【答案】10,,22【解析】当0a=时，B=，此时满足BA，当0a时，22,B

aa=−，此时,AB集合只能是“蚕食”关系，所以当,AB集合有公共元素21a−=−时，解得2a=，当,AB集合有公共元素22a=时，解得12a=，故a的取值集合为10,,22.故答案为：10,,

224．（2022·全国·高三专题练习）若xA，则1Ax，就称A是伙伴关系集合，集合111,0,,,1,2,3,432M=−的所有非空子集中，具有伙伴关系的集合个数为_________________.【答案】15【解析】因为1A，111A=；1A−，111A=

−−；2A，12A；3A，13A；这样所求集合即由1，1−，“3和13”，“2和12”这“四大”元素所组成的集合的非空子集．所以满足条件的集合的个数为42115−=，故答案为：15.考点四集合与其他知识的综合运用【例4-1】（2022·全国·高

三专题练习）已知i是虚数单位，集合MZ=（整数集）和()2211,,,iNiiii+=的关系韦恩图如图所示，则阴影部分所示的集合的元素共有（）A．3个B．2个C．1个D．无穷个【答案】B【解析】因为21i=−，()2211222iiii

iii+++===，所以集合1,1,,2Nii=−，因为阴影部分所示的集合为MN，MZ=，所以1,2MN=−，阴影部分所示的集合的元素共有2个，故选B．【例4-2】（2022·全国·模拟预测（理））已知函数()()()2sin0

,0gxx=+的部分图象如图所示，将函数()gx的图象向右平移6个单位长度，得到函数()fx的图象，若集合()3512Axyfxf==−，集合0,1,2B=，则AB=______．【答

案】0【解析】由图可知()gx周期52=1212T=+，∴22T==．由212πg−=得22122k−+=+，∴223k=+，kZ，∵0，∴k取0，23=，∴()22sin23gxx

=+，∴()22sin22sin2633fxxx=−+=+，∴35352sin22sin611212363f=+=−+=

．∴()35150sin22221232636fxfxkxk−++++，kZ，∴,124Axkxkk=−+Z，∴0AB=．故答案为：0﹒【一隅三反】1．

（2022·上海·高三专题练习）已知互异的复数,ab满足0ab，集合,ab={2a,2b},则ab+=（）A．2B．1C．0D．1−【答案】D【解析】由题意22{aabb==或22{abba==，因为ab，0ab，1322{1322aibi=−+=−−

1322{1322biai=−+=−−或，因此1ab+=−．选D.2．（2022·福建福州·模拟预测）从集合1,2,3的非空子集中任取两个不同的集合A和B，若AB，则不同的取法共有（）A．42种B．36种C．30种D．15种【答案】C【解析】若集合A仅有1个元素，则集合A有

133C=种取法；集合B有2213−=种取法；此时共有339=种取法；若集合A中有2个元素，则集合A有233C=种取法；集合B有112215CC++=种取法；此时共有3515=种取法；若集合A中有3个元素，则集合B为1,2,3的非空真子集，

有3226−=种取法；此时共有166=种取法；综上所述：不同的取法共有915630++=种.故选：C.3．（2022·全国·高三专题练习）函数2,0()4sin,0xxfxxx=，则集合|[()]0xffx=元素的个

数有（）A．2个B．3个C．4个D．5个【答案】D【解析】当0x时，()20fxx==，解得0x=，当0x时，若()4sin0fxx==，解得x=，当0x时，若()2fxx==，解得x=−，当0x时，若()4sinfxx==，则sin4x=，解得arc

sin4x=或arcsin4−.又∵()0ffx=∴()0fx=或()fx=∴0x=或x=或x=−或arcsin4x=或arcsin4x=−.∴集合()0xffx=元素的个数有5个.故选：D．