【文档说明】《【一隅三反】2023年高考数学一轮复习（提升版）（新高考地区专用）》5.4 正、余弦定理（精讲）（提升版）（解析版）.docx，共(24)页，1.643 MB，由envi的店铺上传

转载请保留链接：https://www.doc5u.com/view-c51937b88686ce1c580b8f0a236a74ef.html

以下为本文档部分文字说明：

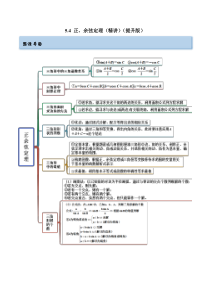
5.4正、余弦定理（精讲）（提升版）思维导图考点一判断三角形的形状【例1】（2022·全国·高三专题练习）（多选）已知a，b，c分别是ABC三个内角A，B，C的对边，下列四个命题中正确的是（）A．若tantantan0ABC++，则ABC是锐角三角形B．

若coscosaAbB=，则ABC是等腰三角形C．若coscosbCcBb+=，则ABC是等腰三角形D．若coscoscosabcABC==，则ABC是等边三角形【答案】ACD【解析】对于A，因为()tantantan1tan

tanABABAB++=−，所以()()tantantan1tantanABABAB+=+−，()()tantantatan1tantantnnaABBACACB++=+−+()tan1tantantantantanta

n0CABCABC=−−+=，因为A，B，C为ABC的内角，所以A，B，C都是锐角，所以ABC是锐角三角形，故选项A正确；对于B：由coscosaAbB=及正弦定理，可得sincossincosAABB=，即sin2si

n2AB=，所以22AB=或22πAB+=，所以AB=或π2AB+=，所以ABC是等腰三角形或直角三角形，故选项B错；对于C：由coscosbCcBb+=及正弦定理化边为角，可知sincossincossinBCCBB+=，即sinsinAB=，因为A，B为ABC的内角，所以AB

=，所以ABC是等腰三角形，故选项C正确；考点呈现例题剖析对于D：由coscoscosabcABC==和正弦定理化边为角，易知sinsinsincoscoscosABCABC==，所以tantantanABC==，因为A，B，C为ABC的内角，所以ABC==，所以AB

C是等边三角形，故选项D正确；故选：ACD.【一隅三反】1．（2022·全国·高三专题练习）在△ABC中，内角A，B，C的对边分别为a，b，c已知21sin222Abc+=，则△ABC的形状为（）A．直角三角形B．等边三角形C．等

腰三角形D．等腰直角三角形【答案】A【解析】∵21sin222Abc+=，可得2sin22Acbc−=，∴21cos1222Acbbcc−−==−，∴cosbAc=，∵222cos2bcabAbcc+−==，∴22222bcab+−=，

∴222bac+=，∴ABC为直角三角形，且90C=，故选：A.2．（2022·全国·高三专题练习）设△ABC的三边长为BCa=，=CAb，ABc=，若tan2Aabc=+，tan2Bbac=+，则△ABC是（）．A．等腰三角形B．直角三角形C．等腰三角形或

直角三角形D．等腰直角三角形【答案】B【解析】设()12Pabc=++，△ABC的内切圆半径为r，如图所示，法一：∴tan2Arapabc==−+①；tan2Brbpbac==−+②.①÷②，得：pbaacpabcb−+=−+，即()()()()22pbaacpabbc−+=−+．于是()()

()()bbccabaacbca++−=++−，232232abbbcabaac−+=−+，()()2220ababc−+−=，从而得ab=或222+=abc，∴AB=或90C=．故△ABC为等腰三角形或直角三角形，（1）当ab=时

，内心I在等腰三角形CAB的底边上的高CD上，2211224ABCcSABCDac==−△，从而得22242ccaSrabcac−==+++．又()1122pabcac−=+−=，代入①式，得()224122ccaaabcacacc−==+++，即

2242acaacac−=++，上式两边同时平方，得：()2222acaacac−=++，化简2220ca−=，即2ca=．即△ABC直角三角形，∴△ABC为等腰直角三角形．（2）当222+=abc时，易得()12rabc=+−．代入②

式，得()()1212abcbacacb+−=++−，此式恒成立，综上，△ABC为直角三角形．法二：利用sintan21cosAAA=+，sintan21cosBBB=+及正弦定理和题设条件，得sinsin1cossinsinAAABC=++①，sinsin1cossinsinBBBAC=

++②.∴1cossinsinABC+=+③；1cossinsinBAC+=+④.由③和④得：1cossin1cossinABBA+−=+−，即sincossincosAABB+=+，ππsinsin44AB+=+

，因为,AB为三角形内角，∴ππ44AB+=+或πππ44AB+=−−，即AB=或π2AB+=．（1）若AB=，代入③得：1cossinsinABC+=+⑤又ππ2CABA=−−=−，将其代入⑤，得：1cossinsin2AAA+=+．变形得()()2sincossincos0AAA

A−−−=，即()()sincossincos10AAAA−−−=⑥，由AB=知A为锐角，从而知sincos10AA−−．∴由⑥，得：sincos0AA−=，即π4A=，从而π4B=，π2C=．因此，△ABC为等腰直角三角形．（2）若π2AB+=，即

π2C=，此时③④恒成立，综上，△ABC为直角三角形．故选：B3．（2022·全国·高三专题练习）已知ABC的三条边,,abc和与之对应的三个角,,ABC满足等式coscoscoscoscoscosaBbCcAbAcBaC++=++则此三角形的形状是

（）A．等腰三角形B．直角三角形C．等腰或直角三角形D．等腰直角三角形【答案】A【解析】，可得222222222222222222222222acbabcbcabcaacbabcabcbcaacabbcbcacab+−+−+−+−+−+−++=++，整理，得2222220abbccac

ab−−−++=，所以222222220abbccbbacab−−−+−++=，所以()()22221111+0abbccbab−−−−=，所以()()()()+0abbcabbcbabcbcab++−−−−=，所以()()0abbcabbcbc

ab++−−−=，所以()()220aabbccabbcabc−−−−−=，所以()()()0acbabbcacabc++−−−=，所以ab=或bc=或ac=，故三角形为等腰三角形.故选：A

4．（2022·全国·高三专题练习）（多选）设ABC的三个内角A，B，C所对的边分别为a，b，c．下列有关等边三角形的四个命题中正确的是（）．A．若sinsinsinabcABC==，则ABC是等边三角形B．若coscoscosabcABC==，则ABC是等边三角形C．若ta

ntantanabcABC==，则ABC是等边三角形D．若abcABC==，则ABC是等边三角形【答案】BCD【解析】A，若sinsinsinabcABC==，由正弦定理可知：任意ABC都满足条件，因此不一定是等边三角形，不正确；B，若coscoscosabcABC==，由正弦定理可得：si

nsinsincoscoscosABCABC==，∴tantantanABC==，∵(),,0,πABC，∴ABC==，∴ABC是等边三角形，正确．C，若tantantanabcABC==，由正弦定理可得：sinsinsintantantanABCABC==

，∴coscoscosABC==，∵(),,0,πABC，∴ABC==，∴ABC是等边三角形，正确．D，若abcABC==，∴sinsinsinABCABC==，π3ABC===时，ABC是等边三角形；π,,3ABC时，研

究函数()sinπ0,2xfxxx=的单调性，()()22tancoscossinxxxxxxfxxx−−==，π02x时，tanxx，∴函数()fx在π0,2上单调递减，因此sinsinsinABCABC==不成立．综上可得：ABC

是等边三角形，正确．故选：BCD．考点二最值问题【例2-1】（2022·河南·汝州市第一高级中学模拟预测（理））在ABC中，角,,ABC所对的边分别为,,abc，2a=，2cos2cos24sinCAB=+，则ABC面积

的最大值是（）A．23B．1C．43D．2【答案】A【解析】由2cos2cos24sinCAB=+得：22212sin12sin4sinCAB−=−+，即222sinsin2sinACB=+，由正弦定理得：22224ac

b=+=；由余弦定理得：2222cos4abcbcA=+−=，222222coscbbcbcA+=+−，即cos2bAc=，()0,A，22sin14bAc=−，22222421111sin12242

4ABCbSbcAbcbcbc==−=−，2224cb+=，2242cb=−，()2244211194242424ABCSbbbbb=−−=−+，则当289b=时，42max996481644448199bb

−+=−+=，()max142233ABCS==.故选：A.【例2-2】（2022·江西·上饶市第一中学二模（文））在ABC中，角A，B，C所对的边分别为a，b，c，cos(2)cos,3aBcbAa=−=，若点D在边BC上，且2BDDC=，

则AD的最大值是___________.【答案】313+【解析】由cos(2)cos,3aBcbAa=−=，得sincos2sincossincosABCABA=−，因为sin0C，0A，所以1cos,23AA==，设AB

C外接圆的圆心为O，半径为R，则由正弦定理得312sin2sin3aRA===，如图所示，取BC的中点M，在tRBOM中，()2222,12222331BCBMOMOBBM===−=−=；在tRDOM中，222223

33313,323662DMBDBMODOMDM=−=−==+==+313ADAOODROD+=+=+，当且仅当圆心O在AD上时取等号，所以AD的最大值是313+，故答案为：313+．【例2-3】（2022·黑龙江·哈尔滨三中二模）在锐角ABC中，角A，

B，C的对边分别为a，b，c，ABC的面积为S，若222sin()SACba+=−，则1tan3tan()ABA+−的取值范围为（）A．23,3+B．234,33C．234,33D．234,

33【答案】C【解析】在ABC中，1sin()sin,sin2ACBSacB+==，故题干条件可化为22baac−=，由余弦定理得2222cosbacacB=+−，故2coscaBa=+，又由正弦定理化简得：sin2sincossinsincoscossinCABAAB

AB=+=+，整理得sin()sinBAA−=，故BAA−=或BAA−=−（舍去），得2BA=ABC为锐角三角形，故02022032AAA−，解得64A，故3tan13A112

34tantan(,)3tan()3tan33AABAA+=+−故选：C【一隅三反】1．（2022·安徽黄山·二模（理））设ABC的内角,,ABC的对边分别为,,abc，且满足22()sin()+−=abAB22()sin()−+abAB，其中ab¹，若22abc++=+，则AB

C面积的取值范围为______________.【答案】10,2【解析】22()sin()abAB+−=22()sin()−+abAB2222()(sincoscossin)()(sincoscossin)ab

ABABabABAB+−=−+，化简得：222sincos2cossinbABaAB=，由正弦定理可得：222sinsincos2sincossinBABAAB=,sinsin0BA，2sinos2sincosBcBAA=，即sin2sin2BA=，2(0,2),2(0,2)AπBπ

,22AB=或22AB+=，即2AB+=或AB=，又ab¹，2AB+=，即2C=,22cab=+，又22abc++=+，222222(22)ababababab+=++++=+，当仅当ab=时等号成立，1ab，即01ab，11(0,)22△

ABCSab=.故答案为：10,22．（2022·全国·高三专题练习）在ABC中，角A，B，C的对边分别为a，b，c，若3acosC＋b＝0，则tanB的最大值是________.【答案】34【解析】在ABC中，因为3acosC＋b＝0，所以C为钝角，由正弦定理得3s

inAcosC＋sin(A＋C)＝0，3sinAcosC＋sinAcosC＋cosAsinC＝0，所以4sinAcosC＝－cosA·sinC，即tanC＝－4tanA.因为tanA>0，所以tanB＝－ta

n(A＋C)＝－tantan1tantanACAC+−＝tantantantan1ACAC+−＝23tan4tan1AA−−−＝314tantanAA+≤324＝34，当且仅当tanA＝12时取等号，故tanB的最大

值是34.故答案为：343．（2022·全国·高三专题练习）已知锐角ABC外接圆的半径为1，内角A，B，C所对边分别为a，b，c，4B=，则BABC的取值范围是____.【答案】(2,12+【解析】因为2acsinAsinC==，所以2sinaA=，32si

n2sin4cCA==−，所以()2232sin2sin2sincossin224acACABAABAA==−=+22sincos2sinsin2cos212sin214AA

AAAA=+=−+=−+，因为02A，3042A−，所以42A，所以32444A−，故2sin2124A−，即22sin2+1124A−+，所以BABC的取值范围是(2,12+.故

答案为：(2,12+.4．（2022·甘肃·二模（理））如图，在圆内接四边形ABCD中，2,4ABBC==，且,,ACBCBABAC依次成等差数列.(1)求边AC的长；(2)求四边形ABCD周长的最大值.【答案】(1)23(2)10【解析】(1)因为,,A

CBCBABAC依次成等差数列，所以2ACBBACCBA+=，又ACBBACCBA++=，所以3CBA=,又2,4ABBC==，则由余弦定理得:22212cos416224122ACABBCABBCCBA=+

−=+−=，所以23AC=.(2由圆内接四边形性质及3CBA=，知23ADC=，在ADC中，由余弦定理得()22222cosDCCDADACADDCADADDCACD=+−=+−，又因为()24ACCDADDD+（当且仅当ADDC=时“=”成立），所以()22312

4ADDCAC+=，即4ADDC+，则四边形ABCD周长最大值24+4=10+.5．（2022·广东江门·模拟预测）在锐角ABC中，内角A，B，C的对边分别是a，b，c，且满足()(sinsin)()sinabABacC+−=−.(1)求

角B的大小；(2)若23c=，求a的取值范围.【答案】(1)3(2)()3,43【解析】(1)因为()(sinsin)()sinabABacC+−=−，所以由正弦定理可得()()()ababacc+−=−，化简

得222acbac+−=，所以由余弦定理得2221cos222acbacBacac+−===，因为(0,)B，所以3B=(2)因为3B=，所以23ACB+=−=,由正弦定理得，sinsinacAC=，所以31223cossin23s

in2233sin3sinsinsintanCCCcaACCCC+−====+，因为ABC为锐角三角形，所以022032CC−，得62C，所以3tan3C

，所以3033tanC，所以33343tanC+，，所以343a，即a的取值范围为()3,43考点三三角形解的个数【例3-1】（2022·全国·高三专题练习）在ABC中，3a=，3b=，6A=，则此三角形（）A．无解B．一解C．两解D．解的个数不确定【答案】C【解析】在ABC中，3

a=，3b=，6A=，由正弦定理得3sinsin36sin123bABa===，而A为锐角，且ab，则3B=或23B=，所以ABC有两解．故选：C【例3-2】（2022·全国·高三专题练习）在ABC中，内角A，B，C所对的边分别为a，b，c，若4b=，7tan3A=，当

C有两解时，a的取值范围是（）A．()7,4B．()3,4C．()7,3D．(3,4【答案】A【解析】7tan3A=，即sin7cos3AA=,则7sincos3AA=由22227sincoscoscos19AAAA+=+

=，解得29cos16A=,则7sin4A=当C有两解时，sinbAab，则7444a，所以74a，故选：A.【例3-3】（2022·浙江·高三专题练习）ABC中，角A，B，C的对边分别是a，b，c，30A=，3a=，若这个三角形有两解，则b的取值

范围是（）A．36bB．36bC．6bD．6b【答案】B【解析】因为这个三角形有两解，故满足sinbAab，即sin303bb，解得36b.故选：B【一隅三反】1．（2022·全国·高三专题练习）

在ABC中，角A，B，C的对边分别是a，b，c，已知12,30bA==，使得三角形有两解的条件是（）A．6a=B．612aC．12aD．6a【答案】B【解析】12b=，30A=，C到AB的距离sin6hbA==，当6a时，三角形无解，当6a=时，三角形有一解，当6

12a时，三角形有两解，当12a…时，三角形有一解．故选：B．2．（2022·全国·高三专题练习）在ABC中，角A，B，C的对边分别是a，b，c，若，满足条件3a=，60A=的三角形有两个，则b的取

值范围是（）A．()2,3B．()3,33C．()3,23D．()22,23【答案】C【解析】因为3a=，60A=，由正弦定理可得sinsinabAB=，所以sin3sin6bABba==，又满足题意的三角形有两个，所以只需sinsin1AB<<，即3

3126b，解得323b.故选：C.3．（2022·全国·高三专题练习）在ABC中，,26Ab==，则“1a”是“ABC有两个解”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件【答案】B【解析】,26Ab

==，若ABC有两个解，则sinbAab，即1222a，即12a，“1a”是“ABC有两个解”的必要不充分条件.故选：B.4．（2022·全国·高三专题练习）在ABC中，角,,ABC所对的边分别为,,abc，下列条件使ABC有两解的是（）A．2,1,30bcA===B．8

,45,65aBC===C．3;2,30acA===D．32,4,45abB===【答案】D【解析】选项A.由余弦定理可得22232cos412125232abcbcA=+−=+−=−ABC的三边分别为2,

1,523bca===−，所以满足条件的三角形只有一个.选项B.45,65BC==，则70A=,由正弦定理可得8sinsinsinsin70bcaBCA===所以8sin458sin65,sin70sin70bc==，ABC的三边为定值，三个角为定

值，所以满足条件的三角形只有一个.选项C.由3;2,30acA===，则由正弦定理可得36sinsinsinsin30bcaBCA====所以21sin63C==,由,ac则AC，所以角C为一确定的角，且0300C，则角角B为一确定的角，从而边b也

为定值，所以满足条件的三角形只有一个.选项D.作45B=,在BÐ的一条边上取32BCa==，过点C作CH垂直于BÐ的另一边，垂足为H.则3CH=,以点C为圆心，4为半径画圆弧，因为432CHa=，所以圆弧与BÐ的另一边有两个交点12,AA所以12,BACBAC均满足条件，所以所

以满足条件的三角形有两个.故选：D考点四几何中的正余弦定理【例4】（2022·浙江宁波·二模）如图，在ABC中，73BC=，1cos3A=，点M是线段AC的三等分点（靠近点A），若23BABM=，则sinAMB=___________，AB

C的面积是___________.【答案】42962【解析】在ABC中，因为1cos3A=，可得22sin3A=，由73BC=，且23BABM=，在ABM中，由正弦定理sinsinABBMAMBA=，可得22242sinsin339ABAMBABM===，因为sinsinAAMB

，所以AMB为锐角，所以7cos9AMB=，又由coscos()cos()ABMAAMBAAMB=−−=−+1722421(coscossinsin)()39393AAMBAAMB=−−=−−=，所以ABMA=，所以AMBM=，设AMBMx

==，因为23BABM=且点M是线段AC的三等分点，可得2,33ABxACx==，在ABC中，由余弦定理可得2222cosBCABACABBCA=+−，即2242173923933xxxx=+−，解得29x=，所以3x=，所以2,9ABAC==，所以AB

C的面积为122296223ABCS==.故答案为：429；62.【一隅三反】1．（2022·山东烟台·一模）如图，四边形ABCD中，222ABBCABBCAC++=．(1)若33ABBC==

，求△ABC的面积；(2)若3CDBC=，30CAD=，120BCD=，求∠ACB的值．【答案】(1)334(2)∠ACB=45【解析】(1)在△ABC中，2221cos222ABBCACABBCBABBCABBC+−−

===−，因为0180B，所以120B=．11333sin120312224ABCSABBC===△．(2)设ACB=，则120ACD=−，30ADC=+，60BAC=−．在△ACD中，由()sin30sin30ACCD=+，得()sin30sin30ACCD+

=．在△ABC中，由()sin120sin60ACBC=−，得()sin120sin60ACBC=−．联立上式，并由3CDBC=得()()sin30sin1203sin30sin60+=−，整理得()()1sin30s

in604+−=，所以()1sin6022+=，因为060，所以10062068+，所以602150+=，解得45=，即∠ACB的值为45．2．（2022·陕西渭南·二模）如图，在ABC中，角60A=，D为边AC上一点，且31BC=，21BD=，20CD=求：(1)sinC

DB的值；(2)边AD的长.【答案】(1)437(2)15【解析】(1)在BCD△中,由余弦定理的推论得222cos2BDCDBCCDBBDCD+−=,31,21,20BCBDCD===,2222120311cos221207CDB+−==−,01

80CDB,22143sin1cos177CDBCDB=−=−−=(2)CDBABDA=+,ABDCDBA=−,60A=,()sinsinABDCDBA=−()sin60CDB=−sincos60cossin60CDBCDB=−4311353

727214=−−=,在ABD△中,由正弦定理得sinsinADBDABDA=,5321sin1415sin32BDABDADA===3．（2022·广东深圳·一模）如图，在△ABC中，已知2

AB=，62AC=，45BAC=，BC，AC边上的两条中线AM，BN相交于点P．(1)求BAM的正弦值；(2)求MPN的余弦值．【答案】(1)35(2)131050【解析】(1)解：解法1、由余弦定理得222cosACABACCBBABCA+−=，即()2222262226252

2BC=+−=，所以213BC=，所以1132BMCMBC===，在ABM中，由余弦定理，得22229cos213BMAMABAMBMABMAMAM+−+==，在ACM△中，由余弦定理，得222259cos213CMAMACAMCMACMAMAM+−−==，BMA与CMA互

补，则coscos0BMACMA+=，解得5AM=，在ABM中，由余弦定理，得2224cos25ABAMBMBAMABAM+−==，因为0,2BAM，所以23sin1cos5BAMBAM

=−=．解法2、由题意可得，cos4512ABACABAC==，由AM为边BC上的中线，则()12AMABAC=+uuuruuuruuur，两边同时平方得，22211125442AMABACABAC=++=，故5AM=，因为M为BC边中点，则ABM的面积为AB

C面积的12，所以111sinsin222ABAMBAMABACBAC=，即11125sin262sin45222BAM=，化简得，3sin5BAM=．(2)解：方法1、在ABN中，由余弦定理，得22222cos45BNABANABAN

=+−，所以10BN=，由AM，BN分别为边BC，AC上的中线可知P为ABC重心，可得221033BPBN==，21033APAM==，在ABP△中，由余弦定理，得2221310cos250PAPBAB

APBPAPB+−==，又由MPNAPB=，所以1310coscos50MPNAPB==．解法2：因为BN为边AC上的中线，所以12BNANABABAC=+=−+，()22111111322244AMBNABAC

ABACABABACAC=+−+=−−+=，2222111024BNABACABABACAC=−+=−+=，即10BN=．所以131310cos50510AMBNMPNAMBN===．考点五正余弦定理与平面向量的综合运用【例5】（2022

·江西上饶·二模（理））已知ABC的外心为点O，M为边BC上的一点，且2,,13BMMCBACAOAM===，则ABC的面积的最大值等于（）A．32B．3C．368D．364【答案】C【解析】因为2BMMC=，所以()22123333AMABBMABBCABACABABAC=+=+

=+−=+，所以12133AOAMAOABAC==+2212112||||||||33633AOABAOACABACABAC=+=+所以322ABAC，当且仅当23ABAC==时，取等号；所以81sin34236ABCSBA

AABACCBAC==，当且仅当23ABAC==时，取等号；故选：C【一隅三反】1．（2021·全国·高三专题练习）已知ABC中，角A，B，C的对边分别为a，b，c，AH为BC边上的高，以下结论:①()0A

HACAB−=；②0ABBCABC为锐角三角形；③AHACAHsincB=；④22()2cosBCACABbcbcA−=+−其中正确的个数是（）A．1B．2C．3D．4【答案】C【解析】由AH为BC边上的高，∴AHBC⊥，而BCACAB

=−，故()0AHACAB−=，①正确；0ABBC知：向量,ABBC的夹角为钝角，即BÐ为锐角，而无法判断ABC是否为锐角三角形，②错误；|cossinsin|AHACACCAHbCcBAH===，③正确；2222(

)2cosBCACABBCabcbcA−===+−，④正确.故选：C2．（2022·全国·高三专题练习）在ABC中，若2ABABACBABCCACB=++，则ABC是的形状为（）A．等腰三角形B．等边三角形C．直角三角形D．钝角

三角形【答案】C【解析】由2ABABACBABCCACB=++，可得2coscoscoscbcAacBabC=++，又由余弦定理，可得2222222222222bcaacbbacc+−+−+−=++，整理得222bac+=，所以ABC是直角三角形.故选：C.3．（2022·广东佛山·二模

）ABC中，24ABACB==，，O是ABC外接圆圆心，是OCABCACB+的最大值为（）A．0B．1C．3D．5【答案】C【解析】过点O作,ODACOEBC⊥⊥，垂足分别为D，E，如图，因O是ABC外接圆圆心，则D，E分别为AC，BC的

中点，在ABC中，ABCBCA=−，则222||||||2ABCACBCACB=+−，即22||||22CACBCACB+−=，21|cos|2COCACOCAOCACDCACA===，同理21||2COCBC

B=，因此，()OCABCACBOCCBCACACBCOCACOCBCACB+=−+=−+2222211||||2||||||1222CACBCACBCA+−=−+=−，由正弦定理得：||sin2sin||2sin2sinsin4ABBBCABACB===

，当且仅当2B=时取“=”，所以OCABCACB+的最大值为3.故选：C4．（2022·江西上饶·二模（理））已知ABC的外心为点O，M为边BC上的一点，且2,,13BMMCBACAOAM===，则ABC的面积的最大值等于

（）A．32B．3C．368D．364【答案】C【解析】因为2BMMC=，所以()22123333AMABBMABBCABACABABAC=+=+=+−=+，所以12133AOAMAOABAC==+2212112||||||||33633AOAB

AOACABACABAC=+=+所以322ABAC，当且仅当23ABAC==时，取等号；所以81sin34236ABCSBAAABACCBAC==，当且仅当23ABAC==时，取等号；故选：C考点六正余弦定理与其他知识的综

合运用【例6-1】（2022·内蒙古赤峰·模拟预测（理））已知双曲线()2222:10,0xyCabab−=的左、右焦点分别为1F，2F，过点2F的直线与双曲线的右支交于A，B两点．222AFBF=，1260FAF=，则双曲线C的离心率为（）A．2B．3C．133D．5【答案

】C【解析】依题意，设2BFm=，22AFm=，由双曲线的定义得122AFam=+，12BFam=+，在1ABF中，1260FAF=，由余弦定理22211112||||||2||||cosBFAFABAFABFAF=+−，得222(2)(22)93(22)am

ammmam+=++−+，解得3am=，即1268AFmmm=+=，设双曲线的焦距为2c，在12AFF△中利用余弦定理有22224(8)416cmmm=+−，解得13cm=，所以双曲线的离心率为131333cmea

m===．故选：C【例6-2】（2022·辽宁·育明高中高三阶段练习）在ABC中，内角A，B，C所对的边分别为a，b，c，且ABC的面积为234Sa=，且220bckbc+−≤恒成立，则k的最小值为_

_______．【答案】433【解析】由234Sa=得213sin24bcAa=，所以23sin2aAbc=，由余弦定理得222cos2bcaAbc+−=，所以222222223sincos122abcaAAbcbc+−+=+=

，化简得()422222242()0abcabc−++−=，显然关于a的方程有解，所以()()2222224440bcbc=+−−，化简得222133cbc，即333bc．因为220bckbc+−≤恒成立，所以22bcbckbccb+=+恒成立，令=btc，则

333t，而函数()1yfttt==+在3,13上单调递减，在1,3上单调递增，又()()min12ftf==，且()34343,3,333ff==所以()max433ft=．故k的最小值为433．故答案为：433

．【一隅三反】1．（2022·全国·模拟预测）已知1F，2F是双曲线22221xyab−=（0a，0b）的左､右焦点，点M为双曲线的左支上一点，满足1122MFFF=，且125cos16MFF=−，则该双曲线的离心率e=（）A．2B．32

C．3D．2【答案】D【解析】∵11224MFFFc==，由双曲线的定义得21242MFMFaca=+=+，所以采用余弦定理：()()()22222211221211242425cos224216+−+−+===−MFFFMFcccaMFF

MFFFcc，即2291640caca−−=，即291640ee−−=，解得2e=（负值舍去），则该双曲线的离心率2e=.故选：D.2．（2022·江西·模拟预测（理））在ABC中，角,,ABC所对的边分別

为,,abc，满足2sin6bcaC+=+，若函数()()sin22fxx=+的图象向左平移A个单位长度后的图象于y轴对称，则()fx在30,2A的值域为（）A．1,1−B．1,12−C．11,2−D．11,

22−【答案】B【解析】因为2sin6bcaC+=+，故可得31sinsin2sinsincos22BCACC+=+，即sincoscossinsin3sinsinsincosACACCACAC+

+=+，又sin0C，故cos13sinAA+=，联立22sincos1AA+=，可得22cos10AcosA+−=，解得cos1A=−（舍去）或1cos2A=，又()0,A，则3A=，将()()sin2fxx=+向左平移3个单位长度后得到2sin2sin233

yxx=++=++，又因为其为偶函数，故2,32kkZ+=+，故,6kkZ=−，又2，故当0k=时，6=−满足题意，则()sin26fxx=−，322A=，当0,2x

时，52,666x−−，故()1,12fx−.故选：B.3．（2022·全国·哈师大附中模拟预测（理））椭圆C：22221xyab+=（0ab）的左焦点为点F，过原点O的直线与椭圆交于P，Q两点，若∠PFQ=120°，3OF=，7OP=，则椭

圆C的离心率为________．【答案】33【解析】根据题意，取椭圆的右焦点为1F，连接11,PFQF，作图如下：由椭圆的对称性可知，四边形1FPFQ的对角线互相平分，故四边形1FPFQ为平行四边形，则160FPF=；设PFx=，由椭

圆定义可知12PFax=−，在△FOP和△1FOP中由余弦定理可得：2222cosxOFOPOFOPFOP=+−，()22211122cosaxOFOPOFOPFOP−=+−，又1coscosFOPFOP=−，上述两式相加可得：()22220

xax+−=，即2222100xaxa−+−=；在△1FPF中，由余弦定理可得：2221112cos60FFPFPFPFPF=+−，即()()221222xaxxax=+−−−，则()28xax−=，228xax−+=；故可得29a=，则3a=，又3c

=，故椭圆离心率为33ca=.故答案为：33.