【文档说明】《【一隅三反】2023年高考数学一轮复习（提升版）（新高考地区专用）》3.6 零点定理（精讲）（提升版）（解析版）.docx，共(16)页，1.616 MB，由envi的店铺上传

转载请保留链接：https://www.doc5u.com/view-9d5c5ee659de953bab3147feb3efcc79.html

以下为本文档部分文字说明：

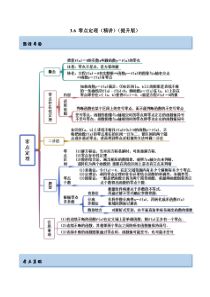
3.6零点定理（精讲）（提升版）思维导图考点呈现考点一零点的区间【例1】（2022·河南开封·）函数41()log2fxxx=−的一个零点所在的区间是（）A．(0,1)B．(2,3)C．(2,e)D．(1,2)【答案】D【解析】因为41()log2fxxx=−，()fx的定义

域为()0+，，211()0ln42fxxx=+，所以()fx在()0+，上单调递增，所以411(1)log10022f=−=−，41111(2)log204244f=−=−=，由零点存在性定理知：()()120ff，函数

41()log2fxxx=−的一个零点所在的区间是(1,2).故选：D.【一隅三反】1．（2022·湖南）函数()233xfxx=+−的零点所在区间是（）A．10,2B．1,12C．31,2D

．3,22【答案】B【解析】因为()fx是R上的增函数，且()1320,12022ff=−=，所以()fx的零点在区间1,12内.故选：B2．（2022·四川攀枝花）已知函数()lg27fxxx=+−的零点在区间()(),1kkkZ+

上，则k=（）A．1B．2C．3D．4【答案】C【解析】函数()fx的定义域为(0,)+，且在(0,)+上单调递增，故其至多一个零点；例题剖析又()3lg310f=−，()4lg410f=+，故()fx的零点在区间()3,4，故3k=.故选：C．3．（2022·云南德宏

）方程lg2xx+=的解所在的区间为（）A．(0,1)B．(1,2)C．(2,3)D．(3,4)【答案】B【解析】设()lg2fxxx=+−，易知()fx在定义域(0,)+内是增函数，又(1)10f

=−，(2)lg20f=，所以()fx的零点在(1,2)上，即题中方程的根属于(1,2)．故选：B．考点二零点的个数【例2-1】（2022·陕西）函数()222,0,23,0lnxxxxfxxxx−+=−−的零点个数为（）A．0

B．1C．2D．3【答案】D【解析】当0x时，2()0ln2fxxxx==−则函数()fx的零点个数为函数lnyx=与函数22yxx=−，()0,x+的交点个数作出两个函数的图象如下图所示，由图可知，当0x时，函数()fx的零点有两个

，当0x时，2()2301fxxxx=−−==−，即当0x时，函数()fx的零点有一个.综上，函数()fx的零点有三个.故选：D【例2-2】（2022·山西）已知())())31,0,1,2

1,1,.xxfxfxx−=−+若()()gxfx=−，则()gx在0,10内的零点个数为（）A．8B．9C．10D．11【答案】B【解析】作出()fx的图像，则()gx在0,10内的零点个数为曲线()yfx=与直线y=

在0,10内的交点个数9.选：B.【一隅三反】1．（2022·安徽）已知函数()2,0,2,0,xfxxxx=+„则方程()20xfx−=的解的个数是（）A．0B．1C．2D．3【答案】C【解析】令()20xfx−=

，得()2xfx=，则函数()2xfx−零点的个数即函数()fx与函数2xy=的交点个数．作出函数()fx与函数2xy=的图像，可知两个函数图像的交点的个数为2，故方程()20xfx−=的解的个数为2个．故选：C．2．

（2022·全国·高三专题练习）函数()()ln3fxx=+的图像与函数()22gxx=−的图像的交点个数为（）A．2B．3C．4D．0【答案】C【解析】()fx在(3,)−+上是增函数，()gx在(,2)−−和(0,2)上是

减函数，在(2,0)−和(2,)+上是增函数，(2)0f−=，(2)(2)0gg−==，(0)2(0)ln3gf==，作出函数()fx()gx的图像，如图，由图像可知它们有4个交点．故选：C．3．（2022·海南省）设函数()fx定义域

为R，(1)fx−为奇函数，(1)fx+为偶函数，当(1,1)x−时，2()1fxx=−+，则函数()lgyfxx=+有（）个零点A．4B．5C．6D．7【答案】C【解析】()lgyfxx=+的零点个数即(),lgyfxyx==−的图象交点个数.因为(1

)fx−为奇函数，故(1)fx−关于原点对称，故()fx关于()1,0−对称，又(1)fx+为偶函数，故()fx关于1x=对称，又当(1,1)x−时，2()1fxx=−+，画出图象，易得函数(),lgyfxyx==−的图象有6个交点故选：C考点三比较零点的大小

【例3】（2022·安徽）已知函数()2xfxx=+，2()loggxxx=+，()2sinhxxx=+的零点分别为a，b，c则a，b，c的大小顺序为（）A．abcB．bacC．cabD．bca【答案】

D【解析】由()2sin0hxxx=+=得0x=，0c=，由()0fx=得2xx=−，由()0gx=得2logxx=−.在同一平面直角坐标系中画出2xy=、2logyx=、yx=−的图象，由图象知0a，0b，acb

.故选：D【一隅三反】1．（2022·河南）若实数,,abc满足()32ln1,2log,2lnabcabc−−−=+==，则（）A．cbaB．acbC．cabD．bac【答案】B【解析】画出2xy−=与()

3ln1,log,lnyxyxyx=+==三个函数的图象，如图可得2xy−=的与()3ln1,ln,logyxyxyx=+==交点的横坐标依次为,,acb，故acb故选：B2．（2022·安徽）已知1120xx+=，222log0xx+=，3233log0xx−−=，则（）A．123

xxxB．213xxxC．132xxxD．231xxx【答案】A【解析】设函数()2xfxx=+，易知()fx在R上递增，()112f−=−，()01f=，即()()100ff−，由零点存在定理可知．110x−；设函数()2loggxxx=+，易知()gx在(

)0,+上递增，1122g=−，()11g=，即()1102gg，由零点存在定理可知，2112x；设函数()21log3xhxx=−，易知()hx在()0,+上递减，()113h=，()30hx=，因为()()31hh

x，由函数单调性可知，31x，即123101xxx−.故选:A．3．（2022·山西）正实数,,abc满足422,33,log4ababcc−+=+=+=，则实数,,abc之间的大小关系为（）A．bacB．abcC．acdD．bca【

答案】A【解析】22aa−+=，即220aa−+−=，即22aa−=−，2xy−=与2yx=−的图象在()0,+只有一个交点，则220xx−+−=在()0,+只有一个根a，令()22xfxx−=+−，()21222204f−=+−=，()11112202f−=

+−=−，()()120ff，则12a；33bb+=，即330bb+−=，即33bb=−，由3xy=与3yx=−的图象在()0,+只有一个交点，则330xx+−=在()0,+只有一个根b，令()33xgxx=+−，()113

310g=+−=，121153330222g=+−=−，()1102gg，故112b；4log4cc+=，即4log4cc=−，即4log40cc+−=，由4logyx=与4yx=

−的图象在()0,+只有一个交点，则4log40xx+−=在()0,+只有一个根c，令()4log4hxxx=+−，()444log4410h=+−=，()4433log34log310h=+−=−，()()340hh，则34c；bac故选：A.考点四已知零点求参数【例

4-1】（2022·山东潍坊）已知函数3()3fxxx=−的图像与直线ym=有3个不同的交点，则实数m的取值范围是（）A．(2,)−+B．(2,2)−C．(,2)−D．(,2)(2,)−−+【答案】B【解析】对函数

3()3fxxx=−求导得：2()333(1)(1)fxxxx=−=+−，当1x−或1x时，()0fx，当11x−时，()0fx，即()fx在(,1)−−，(1,)+上单调递增，在(1,1)−上单调递减，()fx在1x=−处取得极大值(1

)2f−=，在1x=处取得极小值(1)2f=−，在同一坐标系内作出函数3()3fxxx=−的图像和直线ym=，如图，观察图象知，当22m−时，函数3()3fxxx=−的图像与直线ym=有3个不同的交

点，所以实数m的取值范围是(2,2)−.故选：B【例4-2】（2022·吉林）已知()3,0e3,0xxxfxxxx=−若关于x的方程()fxa=有3个不同实根，则实数a取值范围为（）A．12e−

，B．()2,0−C．1e−，D．10e，【答案】D【解析】因为0x时，()exxfx=，则1()exxfx−=，令()0fx=，则1x=，所以()0,1x时，()0fx，则()fx单调递增；()1,x+时，()

0fx，则()fx单调递减；且(0)0f=，1(1)ef=，x→+时，()0fx→；0x时，3()3fxxx=−，则2()33fxx=−，令()0fx=，则1x=−，所以()1,0x−时，()0fx，则()fx单调递增；(),1x−−时，()0fx，则(

)fx单调递减；且(0)0f=，()12f−=−，x→−时，()fx→+；作出()fx在R上的图象，如图：由图可知要使()fxa=有3个不同的实根，则10ea.故选：D.【例4-3】（2022·安徽·合肥市）已知函数()sin(0)3=+−

fxx在区间70,3上有且仅有4个零点，则的取值范围是（）A．(0,1)B．3,12C．1,12D．[1,2]【答案】B【解析】根据题意，函数()sin(0)3=+−fxx

，若()0fx=，即sin3x+=，必有01，令7,0,33txx=+，则833t，设()8sin,,33gttt=，则函数(

)ygt=和y=在区间8,33内有4个交点，又由于83sinsin332==，必有312，即的取值范围是3,12，故选：B.【一隅三反】1．（2022·全国·高三专题练习）已知函数()22,02,0xxfx

xxx−=−+若关于x的方程()12fxxm=+恰有三个不相等的实数解，则m的取值范围是（）A．30,4B．30,4C．90,16D．90,16【答案】D【解析】函数()22,0,2

,0xxfxxxx−=−+的图像如下图所示：若关于x的方程()12fxxm=+恰有三个不相等的实数解，则函数()fx的图像与直线12yxm=+有三个交点，若直线12yxm=+经过原点时，m＝0，若直线12yxm=+与函数()12fxxm=+的图像相切

，令22123022xxxmxxm−+=++−=，令9940416mm=−==.故90,16m.故选：D．2．（2022·河南·模拟预测（理））已知函数()fx为定义在R上的单调函数，且()()2210xffxx−−=．若函数()()22,0,log1,0

fxxaxgxxax−−=−−有3个零点，则a的取值范围为（）A．(2,3B．(1,3−C．(3,4D．(1,4−【答案】A【解析】因为()fx为定义在R上的单调函数，所以存在唯一的Rt，使得()10ft=，则()22xfxxt−−=，()22tfttt

−−=，即()2310tftt=+=，因为函数23tyt=+为增函数，且223210+=，所以2t=，()222xfxx=++.当0x时，由()0gx=，得22xa=+；当0x时，由()0gx=，得2log1ax=−.结合函数的图象可知，若()gx有3个零

点，则(2,3a．故选：A3．（2022·广西·贵港市高级中学三模）已知23sin2cos1(0)2xx+=在(0,2)x有且仅有6个实数根，则实数的取值范围为（）A．3,22B．3,22C．35,23

D．35,23【答案】D【解析】由()23sin2cos102xx+=，得()311sin2cos20222xx+=，即1sin(2)62x+=.设()sin26fxx=+，即()12fx=在()0,2x

有且仅有6个实数根，因为24666x++，故只需5646666+++，解得3523，故选：D．4．（2022·山西）已知函数()31,21()1,2xxfxxx−=

−，若函数()()gxfxkxk=−+恰好有两个零点，则实数k的取值范围是（）A．)1,+B．()0,1C．()1,+D．()(),00,1−【答案】C【解析】由题意知，画出函数()31,21()1,2xxfxxx−=−的简图，如图所示由()()gx

fxkxk=−+恰好有两个零点转化为()fx与直线()1ykx=−有两个不同的交点，由图知，当直线经过点()()1,0,0,1−两点的斜率为10101k−−==−，则1k.所以实数k的取值范围为()1,+.故选：C.考点五零点的综合运用【例5-1

】（2022·新疆克拉玛依）函数()()1sinfxxx=−−在区间3722−,上的所有零点之和为（）A．0B．2C．4D．6【答案】C【解析】因为()()1sinfxxx=−−，令()0fx=，即()1

sinxx=−，当x=时显然不成立，当x时1sinxx=−，作出sinyx=和1yx=−的图象，如图，它们关于点(,0)对称，由图象可知它们在3722−,上有4个交点，且关于点(,0)对称，每对

称的两个点的横坐标和为2，所以4个点的横坐标之和为4．故选：C．【例5-2】（2022·甘肃）若函数2()(1)1xfxmxx=−−+在区间(1,1)−上有2个零点()1212,xxxx，则21exx+的取值范围是（）A．(1,e1)−B．(2,e1)+C．(1

,)+D．(e1,)−+【答案】A【解析】函数2()(1)1xfxmxx=−−+在区间(1,1)−上有2个零点12,xx即方程221xmx=−在区间(1,1)−上有2个实数根12,xx设()221xgxx=−，则()gx为偶函数.且()222221111111xxgxxxx−+==

=+−−−当0x=时，()00g=，当01x时，21yx=−在()0,1上单调递增，且210x−所以()gx在()0,1上单调递减，则在()1,0−上单调递增，又1x→时，()gx→−；1x→−时，()gx→−，则

()gx的大致图像如图.所以方程221xmx=−在区间(1,1)−上有2个实数根12,xx满足122,01xxx=−则2212eexxxx=−+，设()exhxx=−，则()e10xhx=−在()0,1上恒成立所以()2212ee1,e1xxxx=−−+故选：

A【例5-3】（2022·全国·高三专题练习）已知函数()e2xfxx=+−的零点为a，函数()ln2gxxx=+−的零点为b，则下列不等式中成立的是（）A．ln2+aebB．ln2+aebC．223ab+D．1ab【答案】C【解析】令()0fx=、()0gx

=，则e2xx=−、ln2xx=−，在同一坐标系中分别绘出函数exy=、lnyx=、2yx=−的图像，因为函数()e2xfxx=+−的零点为a，函数()ln2gxxx=+−的零点为b，所以(),eaAa，(),lnBbb，解方程组211y

xxyxy=−===，因为函数xye=与lnyx=互为反函数，所以由反函数性质知A、B关于()1,1对称，则2ab+=，eln2ab+=，()214abab+=，A、B、D错误，因为()e10xfx=+，所

以()fx在R上单调递增，因为()010f=−，13e022f=−，所以102a，因为点(),aAae在直线2yx=−上，所以2=−=aeab，22221ee34aaba+=++，故C正确，故选：C．【一隅三

反】1．（2022·安徽·合肥一六八中学）若()fx为奇函数，且0x是()2exyfx=−的一个零点，则0x−一定是下列哪个函数的零点（）A．()e2xyfx−=−−B．()e2xyfx=+C．()e2xyfx=−D．()e2xyfx=−+【答案】B【解析】()fx是奇函数，()()fxfx

−=−且0x是()2e=−xyfx的一个零点，所以()002exfx=，把0x−分别代入下面四个选项，对于A，()()0020ee222−=−xxfx，不一定为0，故A错误；对于B，()()0000e2exxfxfx−−−

+=−0012ee20xx−+=−+=，所以0x−是函数()e2xyfx=+的零点，故B正确；对于C，()000224e2e−−−=−−=−xfx，故C不正确；对于D，()0000e22ee+24−−+==xxxfx，故D不正确；故选：B.2．（2022·陕西·模拟预测（理））已知

1x是方程32xx=的根，2x是方程3log2xx=的根，则12xx的值为（）A．2B．3C．6D．10【答案】A【解析】方程32xx=可变形为方程23xx=，方程3log2xx=可变形为方程3log2xx=，1x是方程32xx=的根，2x是方程3log2xx=的根，1x是函数3

xy=与函数2yx=的交点横坐标，2x是函数3logyx==与函数2yx=的交点横坐标，函数3xy=与函数3logyx=互为反函数，函数3logyx=与函数2yx=的交点横坐标2x等于函数3xy=与函数2

yx=的交点纵坐标,即12(,)xx在数2yx=图象上，又2yx=图象上点的横纵坐标之积为2，122xx=，故选：A．3．（2022·陕西·西安中学一模（理））函数(21)()sinln22xfxx+=−−的所有零点之和为_________.【答

案】12【解析】由()0fx=，可得(21)sinln22xx+=−，令(21)sin,ln22xyyx+==−，可得函数(21)sin2xy+=与ln2yx=−的图象都关于直线2x=的对称，在同一坐标系内作出函数(21)sin2xy+=与ln2yx=−的图象，如图所示，由图象可得

，函数(21)sin2xy+=与ln2yx=−的图象有6个公共点，其横坐标依次为123456,,,,,xxxxxx，这6个点两两关于直线2x=的对称，所以1625344xxxxxx+=+=+=，所以1234

5612xxxxxx+++++=，即函数(21)()sinln22xfxx+=−−的所有零点之和为12.故答案为：12.