【文档说明】《【一隅三反】2023年高考数学一轮复习（提升版）（新高考地区专用）》10.1 平面向量的线性运算及基本定理（精讲）（提升版）（原卷版）.docx，共(5)页，439.151 KB，由envi的店铺上传

转载请保留链接：https://www.doc5u.com/view-7258d350fcdccace06f5a674da1d4a56.html

以下为本文档部分文字说明：

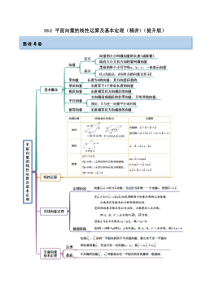
10.1平面向量的线性运算及基本定理（精讲）（提升版）思维导图考点一平面向量的基本定理【例1】（2022·广东·高三开学考试）在ABG中，已知38BEBG=，13AFAG=，AE与BF交于O，则AO=（）A．2173ABBG+B．4

3510ABBG+C．43714ABBG+D．34147ABBG+【一隅三反】1．（2022·广东·高三开学考试）在平行四边形ABCD中，点E、F分别满足12DEEC=，13BFFD=，若ABa=，ADb=，则EF=（

）A．53124ab−B．115124ab−C．133124ab−D．195124ab−2．（2022·江苏·扬州中学高三开学考试）如图所示，在ABC中，点M是AB的中点，且1,2ANNCBN=与CM相交于点E，若AEABAC=+，则,满足（）考点呈现例题剖析A

．45+=B．2=C．25−=D．12=3．（2023·全国·高三专题练习）（多选）在ABC中，D为BC中点，且2AEED=uuuruuur，则（）A．2136CECACB=+B．1133CECACB=+C．CE∥()CACB+D．

CE⊥()CACB−考点二平面向量中的共线问题【例2-1】（2022·全国·高三专题练习）已知向量m，n不共线，向量53OAmn=−，OBxmn=+，若O，A，B三点共线，则x=（）A．53−B．53C．35-D．35【例2-2】（2023·全国·高三专题练习）已知

121242,2MPeePQete=+=+，若M、P、Q三点共线，则t=（）A．1B．2C．4D．－1【一隅三反】1．（2023·全国·高三专题练习）在ABC中，E为AC上一点，3ACAE=，P为BE上任一点，若(0,0)APmABnACmn=+，则

31mn+的最小值是（）A．23B．423+C．6D．122．（2023·全国·高三专题练习）已知ABC的重心为G，经过点G的直线交AB于D，交AC于E，若ADAB=uuuruuur，AEAC=，则11

+=________.3．（2023·全国·高三专题练习）已知向量a，b不共线，若向量43pamb=+与向量3qbma=+共线，则m的值为____________.考点三最值【例3】2（2022·北京·高三开学考试）已知ABC是边长

为2的等边三角形，AB为圆M的直径，若点P为圆M上一动点，则PAPC的取值范围为（）A．[0,4]B．[1,3]−C．[2,4]−D．[3,1]−【一隅三反】1．（2022·浙江）已知A，B，C是圆O上的

三点，CO的延长线与线段BA的延长线交于圆O外的点D，若OCmOAnOB=+，则mn+的取值范围是（）A．()0,1B．()1,+C．(),1−−D．()1,0−2．（2023·全国·高三专题练习）已知,ab是单位向量，0ab=，若向量c满足||1cab−+=，则||cb−的取值范围是（

）A．[21,21]−+B．[1,21]+C．[0,2]D．[51,51]−+3．（2022·全国·高三专题练习）在平面内，定点,,,ABCD满足||||||DADBDC==，2DADBDBDCDCDA===−，动点

P，M满足||1AP=，PMMC=，则2||BM的最大值是（）A．434B．494C．47634+D．372334+考点四平面向量与其他知识综合【例4-1】（2022·全国·高三专题练习）如图，在ABC中，M

，N分别是线段AB，AC上的点，且23AMAB=，13ANAC=，D，E是线段BC上的两个动点，且(,)ADAExAMyANxy+=+R，则12xy+的的最小值是（）A．4B．43C．94D．2【例4-2】（2022·吉林·长春市第二实验中学高三阶段练习）在直角三角形ABC中，90,BP

=在线段AC上，3,1ABBC==，则3BPAP+的最小值为___________.【一隅三反】1．（2022·江苏·阜宁县东沟中学模拟预测）（多选）在平面四边形ABCD中，ABD△的面积是BCD△面积的2倍，又数列na满足12a=，当2n时，恒有()()1122nnnnBDaBAa

BC−−=−++，设na的前n项和为nS，则（）A．na为等比数列B．2nna为递减数列C．na为等差数列D．()152210nnSn+=−−2．（2022·云南·昆明一中高三开学考试）已知任意平面向量(),ABxy→=，把AB→绕其起点沿逆时针方向旋转

角得到向量()cossin,sincosxyxyAP→=−+，叫做把点B绕点A沿逆时针方向旋转角得到点P.已知平面内点()1,1A−，点()13,0B−+，把点B绕点A沿逆时针方向旋转53π得到点P，则向量AB→在向量AP→上的投影向量为___________.（用坐标作答）