【文档说明】《2022-2023学年高一数学一隅三反系列（人教A版2019必修第一册）》1.2 集合间的关系（精讲）（原卷版）.docx，共(6)页，405.609 KB，由envi的店铺上传

转载请保留链接：https://www.doc5u.com/view-137f99497a17ea41fa81e2fe100ea1ae.html

以下为本文档部分文字说明：

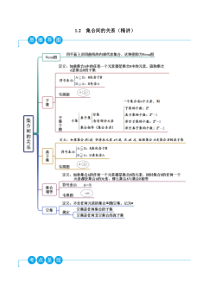
1.2集合间的关系（精讲）考点一集合间的关系【例1-1】（2022·广西桂林）已知集合|2|21AxxBxx=−=−，，则下列关系正确的是（）A．AB=B．ABC．BAD．B蹵【例1-2】（2022·陕西）设集合4,ZMxxnn==，2,Nxxnn==Z，则

（）A．MNB．NMC．MND．NM【一隅三反】1．（2022·全国·高一）有下列关系式：①,,abba=；②,,abba；③=；④0=；⑤0Ü；⑥00．其中不正确的是（）A．①③B．②④⑤C．①②⑤⑥D．③④

1.集合与元素关系：属于不属于2.集合与集合的关系：包含、不包含、真包含温馨提示2（2022·甘肃张掖·高一期末）（多选）下列关系式错误的是（）A．{0}B．{2}{1,2}C．2QD．0Z3．（2022·全国·高一期末）（多选）若集合|3,ZAx

xkk==，|6,ZBxxkk==，则A与B之间最适合的关系是（）A．ABB．ABC．ABD．BA考点二空集【例2-1】（2022·全国·高一课时练习）下列四个集合中，是空集的是（）A．0B．8xx∣，且5xC．210xx−=N∣

D．4xx【例2-2】（2021·北京市）若集合210Axxax=−+==，则实数a的取值范围______．【一隅三反】1．（2022·浙江）下列集合是空集的是（）A．{|0xx或5}x−B．0C．20x

xD．220xx+=2．（2021·全国·高一专题练习）下列命题中正确的是（）A．空集没有子集B．空集是任何一个集合的真子集C．任何一个集合必有两个或两个以上的子集D．设集合BA，那么，若xA，则xB3．（2021·全国·高一课时练习）已知集合M＝{x|2m＜x

＜m＋1}，且M＝∅，则实数m的取值范围是____.考点三集合的（真）子集个数【例3-1】（2022·河南）集合{0,1,2}A=的非空真子集的个数为（）A．5B．6C．7D．8【例3-2】（2022·内蒙古赤峰）已知集合,,Aabc=的所有非空真子集的元素

之和等于12，则abc++的值为（）A．1B．2C．3D．4【一隅三反】1．（2022·安徽省蚌埠第三中学高一开学考试）集合A＝{x|0≤x<3，x∈N}的真子集的个数是()A．7B．8C．16D．42．（2022·江西·高一阶段练习）设集合()20Mxxx=−=，且NM，则满足条件的集合N

的个数为（）A．3B．4C．7D．83．（2022·河北衡水）已知集合221,N43xyAxx=+=，0,1,2,3,4AC，则满足条件的集合C的个数为（）A．2B．3C．4D．5考点四集合相等【例4】（2

022·全国·高三专题练习）下列集合中表示同一集合的是（）．A．()3,2M=，()2,3N=B．10Mxx=+，10Nyy=+C．(),1Mxyxy=+=，1Nyxy=+=D．1,2M=，()1,2N=【一隅三反】

1．（2022·江西新余·高一期末）下列集合与集合20221A=，相等的是()A．(1,2022)B．(),|2022,1xyxy==C．2|202320220xxx−+=D．{(2022,1)}2．（2022·江苏）设集合M={5，x2

}，N={5x，5}．若M=N，则实数x的值组成的集合为（）A．{5}B．{1}C．{0，5}D．{0，1}3．（2022·全国·高一）下列各组两个集合A和B表示同一集合的是（）A．{},{3.14}AB==B．()23,

2,3AB==，C．1,3,π,π,1,3AB==−D．{11,},1AxxxB=−=N∣考点五已知集合关系求参数【例5-1】（2022·江苏）已知集合1,4,Mxx=，21,Nx=，若NM，则实数x组成的集合为（）A．0B．2,2−C．{}2,

0,2-D．{}2,0,1,2-【例5-2】（2022·山西太原）若集合3|01xAxx−=+，{|10}Bxax=+，若BA，则实数a的取值范围是（）A．1,13−B．1,13−C．(

,1)[0,)−−+D．1[,0)(0,1)3−【一隅三反】1．（2022·宁夏·银川一中）已知集合{2,3,1}A=−，集合2{3,}Bm=．若BA，则实数m的取值集合为（）A．{1}B．3C．{1,1}−D．3,3−2．（2022·北京密云）

已知集合{|04,}PxxxZ=，且MP，则M可以是（）A．{1,2}B．{2,4}C．{0,2}D．{3,4}3．（2022·北京工业大学）已知集合2|20Axxx=+−=，|10Bxax=+=，若BA，则实数a的取值组成的集合是（）A．1−B．1

2C．11,2−D．11,0,2−4.（2022·江苏·高一）已知集合3217Axx=−−，集合23Bxaxa=+，若BA，则实数a的取值范围是______.