【文档说明】《【一隅三反】2023年高考数学一轮复习（基础版）（新高考地区专用）》8.3 值域（精讲）（基础版）（原卷版）.docx，共(5)页，485.709 KB，由envi的店铺上传

转载请保留链接：https://www.doc5u.com/view-ae3844dbc542a5b91482807c4b43fa8c.html

以下为本文档部分文字说明：

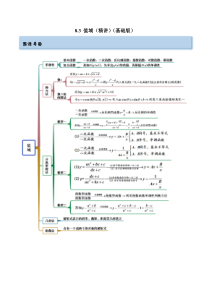
8.3值域（精讲）（基础版）思维导图考点一直接型【例1-1】（2022·全国·高三专题练习）下列函数中，值域为()0,+的是（）A．2yx=B．2yx=C．2xy=D．2logyx=【例1-2】（2022·全国·高三专题练习）（多选）下列函数

中是偶函数，且值域为)0,+的有（）A．()()ln1fxx=+B．1()fxxx=−C．()xxfxee−=+D．42()21fxxx=−+【一隅三反】1．（2022·全国·高三专题练习）函数2()32fxxx=+−

的值域为（）A．[0,4]B．(,2]−C．[2,)+D．[0,2]2．（2022·浙江·高三专题练习）下列函数中，函数值域为(0,)+的是（）A．2(1),(0,)yxx=++B．2log,(1,)yxx=+C．21yx=−D．21yx=−考点呈现例题剖析3

．（2022·河南·模拟预测（文））下列函数中最小值为6的是（）A．226yxx=++B．9|cos||cos|yxx=+C．933xxy=+D．9lnlnyxx=+考点二换元型【例2】（2022·黑龙江）求函数2112yx

x=−−−的值域______．【一隅三反】1．（2022·全国·高三专题练习）函数()1fxxx=+−的值域为___________．2．（2022·全国·高三专题练习）函数()2fxxx=+−的最大值是___．3．（2022·全国·高三专题练习）函数24yxx=−−的值域为__

______．考点三分离常数型【例3-1】（2022·全国·高三专题练习）函数()133xyxx+=−的值域是（）A．()1,+B．()0,+C．()3,+D．()4,+【例3-2】（2022·全国·高三专题练习）函数()2211xxf

xxx−−=++的最大值与最小值的和是（）A．53B．23C．1D．23−【例3-3】（2022·全国·高三专题练习）函数()1221xxfx+=+的值域为（）A．()0,1B．(0,1C．()0,2D．()1

,2【一隅三反】1．（2022·全国·江西科技学院附属中学模拟预测（文））函数23()31xfxx−=+的值域（）A．11,,33−+B．33,,22−+C．

11,,33−−−+D．22,,33−+2．（2022·全国·高一专题练习）求函数2211()212xxyxx−+=−的值域.3．（2022·全国·高三专题练习）求函数34()56xfxx+=+的值域.考点四已知

值域求参数【例4-1】（2022·全国·高三专题练习）已知函数()114,10lg,10axaxyxx−+=的值域为R，则实数a的取值范围是（）A．(),1−B．9,4−+C．9,14−D．9,14−【例4-2】（2022·

全国·高三专题练习）已知函数()24fxxx=−在0,m上的值域为4,0−，则实数m的取值范围是（）A．(0,2B．2,4C．(0,4D．(,2−.【一隅三反】1．（2022·全国·高三专题练习）若函数213()22fxxx=−+的定义

域和值域都是[1,]b，则b=（）A．1B．3C．3−D．1或32．（2022·全国·高三专题练习）已知函数()()343,1log,1axaxfxxx−+=的值域为R，则实数a的取值范围是（）A．()2,4−B．)2,4−C．(,2−−D．

2−3．（2022·全国·高三专题练习）若函数()221++=+xxafxx()0x的值域为),a+，则实数a的取值范围是（）A．(,2−B．[]0,1C．(,1−D．1,2