【文档说明】《【一隅三反】2023年高考数学一轮复习（基础版）（新高考地区专用）》1.1 集合（精讲）（基础版）（解析版）.docx，共(11)页，761.763 KB，由envi的店铺上传

转载请保留链接：https://www.doc5u.com/view-8e5c8e0c4044873bf638bab54d173209.html

以下为本文档部分文字说明：

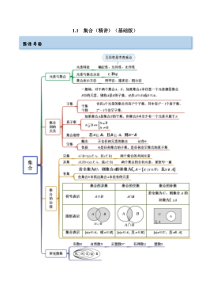
1.1集合（精讲）（基础版）思维导图考点一数集的基本运算【例1-1】（2021·天津·高考真题）设集合1,0,11,3,5,0,2,4ABC=−==，，则()ABC=（）A．0B．{0,1,3,5}C．{0,1,

2,4}D．{0,2,3,4}【答案】C【解析】1,0,11,3,5,0,2,4ABC=−==，，1AB=，()0,1,2,4ABC=.故选：C.【例1-2】（2022·江苏南通·模拟预测）已知集合2|430Axxx=−+，1

1142xBx=∣剟，则AB=（）．A．B．(1,3)C．(1,2]D．[0,3)【答案】D【解析】2|43013Axxxxx=−+=，1110242xBxxx==

∣，所以AB=[0,3).故选：D.【例1-3】（2022·全国·模拟预测（理））设全集U=R，集合102xAxx+=−，集合ln1Bxx=，则AB是（）A．(0,2B．(

)2,e考点呈现例题剖析C．()0,2D．)1,e−【答案】C【解析】102xx+−，解得：12x−，故集合)1,2A=−，ln1x，解得：(0,ex，集合(0,eB=，则()0,2AB=，故选：C．【一

隅三反】1．（2021·湖南·高考真题）已知集合13,5A=,，1,2,3,4B=，且AB=（）A．1,3B．1,3,5C．1,2,3,4D．1,2,3,4,5【答案】A【解析】因为集合13,5A=,，1,2,3,4B=所以1,3AB=，故选：

A.2．（2022·江西·临川一中）已知集合2230Axxx=−−，()ln2Bxyx==−，则AB=（）A．(),3−B．()1,2−C．()0,2D．()2,3【答案】B【解析】∵集合()()31013Axxxxx=−+=−，()l

n2202Bxyxxxxx==−=−=，∴()1,2AB=−.故选：B.3．（2022·黑龙江·齐齐哈尔市）设集合2324,22xMxxNx−==，则MN=（）A．[2,2]−B．51,

4−C．5,4−D．52,4−【答案】D1.离散型数集或抽象集合间的运算,常借用Venn图或观察法求解2.集合中的元素若是连续的实数（常见为不等式）,常借助数轴求解,但要注意端点值能否取到3.解指数对

数不等式时，一般把数字变成跟题目同底数的指数对数，再利用单调性解不等式。4.易错点：对数的真数部分恒大于0方法总结【解析】由24x，得22Mxx=−，由3222x−，解得：54x，所以54Nxx=，所以52,4MN=−，故选：D.考点二点集的基本

运算【例2-1】（2022·上海·高三阶段练习）已知集合(),|10Axyxy=++=，()2,|4Bxyxy==，则AB=()A．{2,2}−B．{2}−C．(2,1)−D．{(2,1)}−【答案】D【解析】210241xyxxyy++==−

==，∴AB={(－2，1)}.故选：D.【例2-2】（2022·河南省直辖县级单位）已知集合()()22,10Mxyxy=++=，()(),ln2Nxyyx==+，则MN=（）A．1,0−B．()1,0−C．

MD．N【答案】D【解析】()()()22,101,0Mxyxy=++==−，因为当1x=−时，()ln2ln10x+==，所以函数()ln2yx=+过点()1,0−，所以MN，所以MNN=.故选：D.【一隅三反】1

．（2022·辽宁）已知集合(),0Axyxy=−=，(),1Bxyxy==，则AB=（）A．()()1,1,1,1−−B．()1,1C．()1,1−−D．【答案】A【解析】解01xyxy−=

=得，11xy=−=−或11xy==，()()1,1,1,1AB=−−．故选：A．2（2022·全国·高三专题练习）已知集合A={（x，y）|x，y为实数，且x2+y2=1}，B=|（x，y）|x，y为如果

集合的元素是点集时，两个集合的交集即为两个方程的交点，一般采用联立方程或几何法解题温馨提示实数，且x+y=1}，则A∩B的元素个数为（）A．4B．3C．2D．1【答案】C【解析】由题得221,{1,xyxy+=+=∴1,{0,xy==或0,{1,xy==A∩B={(1,0),(0,1)}.故选C

.3．（2022·浙江·模拟预测）已知集合22(,)218Sxyxy=+=∣，{(,)29}Tyxyx==−+∣，则ST?（）A．{(3,3)}−−B．{(3,3)}C．{(1,4)}D．{(1,4)}−−【答案】C【解析】29yx=−+的反函数为：922xy=−+联立222

18xy+=与922xy=−+得：2210xx−+=，解得：1x=，代入922xy=−+中，解得：4y=，故交点坐标为()1,4，所以ST?{(1,4)}故选：C考点三元素的互异性【例3-1】（2022

·浙江·高三专题练习）已知aR，bR，若集合2,,1,,0baaaba=+，则20192019ab+的值为（）A．2−B．1−C．1D．2【答案】B【解析】因为2,,1,,0baaab

a=+，所以201baaaba==+=，解得01ba==或01ba==−，当1a=时，不满足集合元素的互异性，故1a=−，0b=，()2019201920192019101ab+=−+=−，故选：B.【例3-2】（2021·甘肃）若以集合A

的四个元素abcd,,,为边长构成一个四边形，则这个四边形可能是（）A．矩形B．平行四边形C．梯形D．菱形【答案】C【解析】由题意，集合A的四个元素abcd,,,为边长构成一个四边形，根据集合中元素的互异性，可得abcd,,,四个元素互不相等

，以四个元素abcd,,,为边长构成一个四边形，结合选项，只能为梯形.故选：C.【一隅三反】1．（2022·浙江·高三专题练习）由实数()22233,,||,,,xxxxxx−−所组成的集合，最多可含有（）个元素A．2B．3C．4D．5【答案】B【解

析】由题意，当0x时所含元素最多，此时()22233,,||,,,xxxxxx−−分别可化为x，x−，2x，所以由实数()22233,,||,,,xxxxxx−−所组成的集合，最多可含有3个元素．故选：B2（2

021·上海市上南中学高三阶段练习）若集合中三个元素为边可构成一个三角形，那么该三角形一定不可能是（）A．锐角三角形B．直角三角形C．钝角三角形D．等腰三角形【答案】D【解析】由集合中元素的互异性可知，这个三角形的三边必须都不相

同，因此不可能为等腰三角形.故选：D.3.（2022·上海民办南模中学高三阶段练习）若31,3,aa−，则实数a的取值集合为______．【答案】0,1,3【解析】因为31,3,aa−，故1a=−或3a=或3aa=，当1a=−时，31a=−，

与元素的互异性矛盾，舍；当3a=时，327a=，符合；当3aa=时，0a=或1a=，根据元素的互异性，0,1a=符合，故a的取值集合为0,1,3.故答案为：0,1,3考点四（真）子集的个数【例4】（2022·全国·模拟预

测）已知集合1,2,3,4,5,6A=，6,1BxxAx=−N，则集合B的子集的个数是（）A．3B．4C．8D．16【答案】C【解析】依题意2,3,4B=，所以集合B的子集的个数

为328=，故选：C.【一隅三反】1（2022·新疆喀什）设集合220,AxxxxZ=−−，则集合*AN∩的元素个数为（）A．0B．1C．2D．3【答案】B【解析】集合2{|20}AxxxxZ=−−，|1201xxxZ=−=，，，所以*{1}AN

=.故选：B.2（2022·重庆实验外国语学校一模）已知集合86AxNNx=−，则集合A的所有非空子集的个数为（）A．5个B．6个C．7个D．8个【答案】C【解析】由题设，86Nx−，即8可被6x−整除且60x−，x

N，∴{2,4,5}A=，故集合A的所有非空子集的个数为3217−=.故选：C3．（2022·福建·模拟预测）设集合{2,1,1,2,3}A=−−，2|log||,ByyxxA==，则集合B元素的个数为（）A．2B．

3C．4D．5【答案】B【解析】当2x=时，y＝1；当1x=时，y＝0；当x＝3时，2log3y=．故集合B共有3个元素．选：B.考点五韦恩图的运用【例5-1】（2022·广东茂名·高三阶段练习）已知全集UZ=，集合1,3,6,7,8A=，0,1,2,3,4B=，则图中阴

影部分所表示的集合为（）A．0,2,4B．2,4C．0,2,3,4D．1,3【答案】A【解析】因为1,3,6,7,8A=，0,1,2,3,4B=，所以1,3AB=，由韦恩图可知阴影部分表示()0,2,4BAB=ð；故选：A【例5-2】（2022·安

徽·合肥一中）设集合U=R，()221xxAx−=，ln(1)Bxyx==−，则图中阴影部分表示的集合为（）A．{x|x≥1}B．{x|1≤x<2}C．{x|0<x≤1}D．{x|x≤0}【答案】D【解析】因为()221−xx等价于()20xx−

，解得02x，所以02Axx=，所以0UAxx=ð或2x，要使得函数()ln1yx=−有意义，只需10x−，解得1x，所以1Bxx=则由韦恩图可知阴影部分表示()UABð{|0}=xx.故选：D.【例5

-3】（2022·贵州贵阳）若全集U和集合A，B的关系如图所示，则图中阴影部分表示的集合为（）A．()UABðB．()UBAðC．()UABIðD．()UABIð【答案】A【解析】由图知：阴影部分属于A，不属于B，故为()UBAð.故选：A【一隅三反】1．（2022·全国）已知全集U=R，集

合13MxZx=−，4,2,0,1,5N=−−，则下列Venn图中阴影部分的集合为（）A．0,1B．3,1,4−C．1,2,3−D．1,0,2,3−【答案】C【解析】集合13{|313}{|

24}1,0,1,2,3MxZxxZxxZx=−=−−=−=−，Venn图中阴影部分表示的集合是{1,2,3}RMN=−ð.故选：C2．（2022·浙江·高三专题练习）已知全集U=R

，集合{|3,}AxxxR=…，{|24}Bxx=−，则图中阴影部分表示的集合为（）A．2,3−B．()2,3−C．(2,3−D．)2,3−【答案】B【解析】由)3,A=+，(2,4)B=−，得U(,3)A=−ð，由图

象可知阴影部分表示的集合为()UABð，所以()()U2,3AB=−ð.故选：B3．（2022·重庆市育才中学高三开学考试）设集合A、B均为U的子集，如图，()UAB∩ð表示区域（）A．ⅠB．IIC．IIID．IV【答案】B【解析】由题意可知

，()UAB∩ð表示区域II.故选：B.考点六集合中的参数问题【例6-1】（2022·湖南·一模）已知集合1,1A=−，1Bxax==，若ABB=，则a的取值集合为（）A．1B．1−C．1,1−D．1,0,1−【答案】

D【解析】由ABB=，知BA，因为1,1A=−，{|1}Bxax==，若B=，则方程1ax=无解，所以0a=满足题意；若B，则1{|1}Bxaxxxa====，因为BA，所以11a=，

则满足题意1a=；故实数a取值的集合为1,0,1−.故选：D.【例6-2】（2022·河南）已知集合()()20Axaxxa=−−，若2A，则实数a的取值范围为（）A．()(),12,−+B

．)1,2C．()1,2D．1,2【答案】D【解析】因为2A，所以()()2220aa−−，解得12a．故选：D．【例6-3】（2022·辽宁朝阳·高三开学考试）已知集合28xAx=，集合Bxxa=，若AB=，则实数a的取值范围为（）A．(,2)−B．(2

,)+C．(,3]−D．[3,)+【答案】D【解析】328223,xxAxxxxBxxa====.又AB=，所以a的取值范围为[3,)+.故选：D【一隅三反】1．（2022·重庆八中高三阶段练习

）设集合|(1)(4)0Axxx=−−，|20Bxxa=+，且{|12}ABxx=，则=a（）A．4B．2C．2−D．4−【答案】D【解析】由题意，集合{|14}Axx=，|20{|}2aBxxaxx=+=−，因为{|12}ABxx=

，可得22a−=，解得4a=−.故答案为：D.2．（2022·全国·江西科技学院附属中学高三阶段练习（理））设集合()()350Axxx=−−，7Bxmx=，若37ABxx=，则实数m的取值范围为（）．A．(3,5B．3,5C．()3,5D．)3,5【答

案】D【解析】()()35035Axxxxx=−−=；而37ABxx=，结合数轴可知，35m，故选：D．3．（2022·全国·高三专题练习）已知集合23,(1)(4)0Ax

axaBxxx=−+=−−，若ABR=，则a的取值范围是（）A．(),1−B．()1,3C．1,3D．)3,+【答案】B【解析】因为()()1401Bxxxxx=−−=或4x，23Axaxa=−+又ABR=，所以

只需2134aa−+，解得13a，故选：B.