【文档说明】《【一隅三反】2023年高考数学一轮复习（基础版）（新高考地区专用）》1.2 逻辑用语与充分、必要条件（精讲）（基础版）（解析版）.docx，共(11)页，702.109 KB，由envi的店铺上传

转载请保留链接：https://www.doc5u.com/view-540b085e7f631394cab942013881bf91.html

以下为本文档部分文字说明：

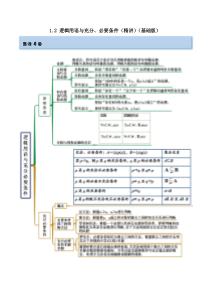
1.2逻辑用语与充分、必要条件（精讲）（基础版）思维导图考点一全称、特称命题的否定【例1-1】（2022·陕西咸阳·二模）已知命题():0,px+，e1xx+，则p为（）A．()0,x+，e1+xx

B．()0,x+，e1+xxC．()0,x+，e1+xxD．()0,x+，e1xx+【答案】C【解析】由全称命题的否定知：():0,px+，e1+xx.故选：C.【例1-2】（2022·全国·东北师大附中）命题“0xR，00e1xx−”的否定是（）A．0x

R，00e1xx−B．0xR，00e1xx−C．xR，e1xx−D．xR，e1xx−【答案】D【解析】命题“0Rx，00e1xx−”为特称量词命题，其否定为Rx，e1xx−；

故选：D【一隅三反】考点呈现例题剖析否定全称命题和特称命题时一是要改写量词，全称量词改写为存在量词，存在量词改写为全称量词；二是要否定结论，而一般命题的否定只需直接否定结论.方法总结1．（2022·安徽安庆·二模）命题p：xR

，10x，则p为（）A．xR，10xB．0xR，010xC．0xR，010xD．0xR，00x【答案】D【解析】由题意，命题:p“xR，10x”可化为命题:p“xR，0x”根据全称命题与存在性命题的关系得：命题:p“xR，0x”的否定:p“0x

R，00x”.故选：D.2．（2022·山西长治）命题2:0,2e1pxxx−+，则p为（）A．20,21xxxe−+B．20,21xxxe−+C．20,2e1xxx−+D．20

,2e1xxx−+【答案】D【解析】由特称命题的否定是全称命题，命题2:0,2e1pxxx−+，所以:p20,2e1xxx−+．故选：D．3．（2022·陕西渭南）设命题π:0,,

sincos4pxxx，则p为（）A．000π0,,sincos4xxxB．000π0,,sincos4xxxC．π0,,sincos4xxxD．π0,,sincos4xxx【答案】A【解析】p为00

0π0,,sincos4xxx.故选：A考点二含有量词的参数问题【例2-1】（2022·陕西宝鸡）若“01,1x−，020xa+−”为假命题，则实数a的最小值为______．

【答案】3【解析】“01,1x−，020xa+−”的否定为“[1,1]x−，都有20xa+−”，因为“01,1x−，020xa+−”为假命题，所以“[1,1]x−，都有20xa+−”为真命题，所以2ax+≥在[1,1]

x−上恒成立，所以3a，所以实数a的最小值为3，故答案为：3【例2-2】（2022·甘肃·甘南藏族自治州合作第一中学）已知命题2:R,230pxaxx++是真命题，那么a的取值范围是（）A．13aB．103aC．13aD．13a【答

案】C【解析】当0a=时，223230axxx++=+仅当32x−时成立，不符合题意；当0a时，若2R,230xaxx++成立，则202430aa−，解之得13a综上，a的取值范围

是13a故选：C【一隅三反】1．（2022·福建宁德）,xR不等式2410axx+−恒成立，则a的取值范围为（）A．4a<-B．4a<-或0a=C．4a−D．40a-<<【答案】A【解析】,

xR不等式2410axx+−恒成立，当0a=时，显然不恒成立，所以0Δ1640aa=+，解得：4a<-.故选：A.2．（2022·全国·高三专题练习）若命题p：“xR，()2110xkx+

−+”是真命题，则k的取值范围是（）A．(),13,−−+B．()3,1−C．()(),31,−−+D．1,3−【答案】D【解析】由题意可知()2110xkx+−+恒成立，所以2(1)40k=−−，解得13k−，故选：D3．（2022·全国

·模拟预测）设命题:[2,1]px−−，34ax，若p为假命题，则实数a的取值范围是______.【答案】1,2−−【解析】由题得:[2,1]px−−，34ax为真命题，所以3max4ax，又函数34yx=在[2,1]−−上单调

递减，所以当2x=−时，max12y=−.故只需12a−.故答案为：1,2−−考点三充分、必要条件的判断【例3-1】（2022·重庆·模拟预测）设aR，则“3a”是“31a”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．

既不充分也不必要条件【答案】A【解析】由31a，即30aa−，即()30aa−，解得3a或0a，所以由3a推得出31a，由31a推不出3a，故“3a”是“31a”的充分不必要条件；故选：A【例3-2】（2022·全国·模拟预测）“2m=−”是“直线1:420lmxy++

=与直线2:10++=lxmy平行”的（）A．充要条件B．必要不充分条件C．充分不必要条件D．既不充分也不必要条件【答案】A【解析】“直线1:420lmxy++=与直线2:10++=lxmy平行”因为2m=−，所以直线1:2

10lxy−−=，直线2:210lxy−+=，1l与2l平行，故充分条件成立；当直线1:420lmxy++=与直线2:10++=lxmy平行时，24m=，解得2m=或2m=−，当2m=时，直线1:210lxy++=与直线2:210lxy+

+=重合，当2m=−时，直线1:210lxy−−=，直线2:210lxy−+=平行，故充要条件成立．故选：A．【一隅三反】1．（2021·天津·高考真题）已知aR，则“6a”是“236a”的（）解题思

路：第一：化简条件和结论第二：根据条件与结论范围的大小进行判断第三：充分不必要条件的判断，一般可根据如下规则判断：（1）若是的必要不充分条件，则对应集合是对应集合的真子集；（2）是的充分不必要条件，则对应集合是对应集合的真子集；（3）是的充分必要条件，则对应集合与对应集合相等；（4

）是的既不充分又不必要条件，对的集合与对应集合互不包含．方法总结A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件【答案】A【解析】由题意，若6a，则236a，故充分性成立；若236a，则6a或6a−，推不出6a，故必要性不成立；所以“6a”是“236a

”的充分不必要条件.故选：A.2．（2020·山东·高考真题）已知aR，若集合1,Ma=，1,0,1N=−，则“0a=”是“MN”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件【答案】

A【解析】当0a=时，集合1,0M=，1,0,1N=−，可得MN，满足充分性，若MN，则0a=或1a=−，不满足必要性，所以“0a=”是“MN”的充分不必要条件，故选：A.3．（2022·江西·临川一中模拟预测）已知直线1:30laxy+−=，直线()2:2130

laxya−−+=，则“1a=−”是“12ll⊥”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件【答案】A【解析】由12ll⊥得：()2130aa−−=，则1a=−或32a=，故1a=−是12ll⊥的充分不必要条件，即A选项正确

.故选：A4．（2022·四川南充·二模（文））设xy､都是实数，则“2x且3y”是“5xy+且6xy”的（）条件A．充分非必要B．必要非充分C．充要D．既非充分也非必要【答案】A【解析】由题意，若2x且3y，由不等式的性质可得5xy+且6xy，故充分性成立

；反之取110xy==，满足5xy+且6xy，但2x且3y不成立，故必要性不成立；故“2x且3y”是“5xy+且6xy”的充分非必要条件故选：A考点四充分、必要条件的选择【例4-1】（2022·陕西·武功县普集高级中学

一模）使不等式2(1)(2)0xx+−成立的一个充分不必要条件是（）A．1x−且2xB．13x-<<C．1xD．3x【答案】D【解析】因为()220x−，故不等式2(1)(2)0xx+−的解集为{1xx−且2}x，故不等式2(1)(2)0xx+−成立的一个充分不必要条件所构成的

集合应是{1xx−且2}x的真子集，显然，满足题意的只有3xx.故选：D.【例4-2】（2022·四川·模拟预测）命题“2[1,3],20xxxa−−−”为真命题的一个充分不必要条件可以是（）

A．4aB．3aC．2aD．1a【答案】A【解析】由题知，命题“2[1,3],20xxxa−−−”为真命题时，满足[1,3]x−，22xxa−.则当[1,3]x−时，222(1)13xxx−=−−，所以命题“2[

1,3],20xxxa−−−”为真命题时，3a.经验证，A选项符合题意；故选：A.【一隅三反】1．（2022·安徽黄山·一模）命题：xR，20020axax−−为假命题的一个充分不必要条件是（）A．(),80,−−+B．()8,0−C．(,0−D．8,0−【

答案】B【解析】命题2,20xRaxax−−”为假命题，命题“xR，220axax−−„”为真命题，当0a=时，20−„成立，当0a时，0a，故方程220axax−−=的280aa=+解得

：80a−„，故a的取值范围是：8,0−，要满足题意，则选项是集合8,0−真子集，故选项B满足题意.故选：B2．（2022·河南·新蔡县第一高级中学）方程22123xymm+=−+表示双曲线的一个充分不必要条件是（）A．30m−B．32m−C．34m

−D．3m【答案】A【解析】方程22123+=−+xymm表示双曲线，则有：()()230mm−+，解可得：32m−，要求方程22123+=−+xymm表示双曲线的一个充分不必要条件，即要求的是32xm−的真子集，依次分析选项：A符合条件.故选

：A.3．（2022·湖北·一模）设，为两个不同的平面，则∥的一个充要条件可以是（）A．内有无数条直线与平行B．，垂直于同一个平面C．，平行于同一条直线D．，垂直于同一条直线【答案】D【解

析】对于A，内有无数条直线与平行不能得出,∥内的所有直线与平行才能得出，故A错；对于B、C，,垂直于同一平面或,平行于同一条直线，不能确定,的位置关系，故B、C错；对于D，,垂直于同一条直线可以得出∥，反之当∥时，若垂于某条直线

，则也垂于该条直线.故选：D.考点五充分、必要条件的判断【例5】（2022·山西晋中·二模）已知条件p：11x−，q：xm，若p是q的充分不必要条件，则实数m的取值范围是（）A．)1,−+B．(),1−−C．()1,0−D．(,1−−【答案】D【解

析】因为p是q的充分不必要条件，所以{11}xx−∣{}xxm∣，即1m−.故选：D.【一隅三反】1．（2022·全国·高三专题练习）已知p：2xa+，q：xa≥，且p是q的充分不必要条件，则实数a的取值范围是（）A．

1a−B．1a−C．1aD．1a【答案】A【解析】由||2xa+可得22axa−−−∴p：22axa−−−又p是q的充分不必要条件，且q：xa≥，∴2aa−−∴1a−故选：A.2．（2022·山东日照·一模）已知条件:12px+，条件:qxa，且p是q的

充分不必要条件，则实数a的取值范围是（）A．[1,)+B．(,1]−C．[3,)−+D．(,3]−−【答案】A【解析】由不等式12x+，可得1x或3x−，所以p：31x−，又由q：xa，因为p是q的充分不必要条件，所以1a

，所以实数a的取值范围为[1,)+.故选：A.3．（2021·浙江·宁波市鄞州高级中学）设mR，若“2x=”是“()22340mxmx−++=”的充分不必要条件，则实数m的值为（）A．12−B．1C．12−或1D．1−或12【答案】A【解

析】由题意可知，2x=是()22340mxmx−++=的解，但不是唯一的解，因此()242340mm−++=，解得1m=或12m=−.当1m=时，2x=是2440xx−+=唯一的解，故不满足题意；当12m=−时，则215404

2xx−+=，即210160xx−+=，解得2x=或8x=，满足题意.综上所述，12m=−.故选：A.4．（2021·江西科技学院附属中学）若“21xm−”的一个充分不必要条件为“12x”，则实数m的

取值范围为（）A．1,12B．1,12C．1,12D．1,12【答案】C【解析】由21xm−，得2121mxm−+，由题意可得12xx2121xmxm−+，所以，211212mm−

+，解得112m.当12m=时，则有12xx02xx，合乎题意.当1m=时，则有12xx13xx，合乎题意.综上所述，112m.故选：C.考点六历史中的充分、必要条件【例6】（2021·安徽）王安石在《游褒禅山记》中写道：“世之奇伟、瑰怪，非常之观

，常在险远，而人之所罕至焉，故非有志者不能至也．”请问“有志”是能到达“奇伟、瑰怪，非常之观”的______条件．（填“充分”“必要”“充要”中的一个）【答案】必要【解析】因为“非有志者不能至”所以“能至是有志者”，因此“有志”是能到达“奇伟、瑰怪，非常之观”的必要条

件.故答案为：必要【一隅三反】1．（2021·湖南长沙市）1943年19岁的曹火星在平西根据地进行抗日宣传工作，他以切身经历创作了歌曲《没有共产党就没有中国》，后毛泽东主席将歌曲改名为《没有共产党就没有新中国》．2021年是中国共产党建党100

周年，仅从逻辑学角度来看，“没有共产党就没有新中国”这句歌词中体现了“有共产党”是“有新中国”的（）A．充分条件B．必要条件C．充要条件D．既不充分也不必要条件【答案】B【解析】从逻辑学角度，命题“没有共产党就没有新中国”的逆否命题是“有了新中国就有了

共产党”，因此“有共产党”是“有新中国”的必要条件，故选：B．2．（2022·新余市第一中学）“黄沙百战穿金甲，不破楼兰终不还”是我国唐代著名诗人王昌龄的《从军行》中的两句诗，描写了当时战事的艰苦以及戍边

将士的豪情壮志，从逻辑学的角度看，最后一句中，“破楼兰”是“终还”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件【答案】B【解析】“破楼兰”不一定“终还”，但“终还”一定是“破楼兰”，

由充分条件和必要条件的定义判断可得“攻破楼兰”是“返回家乡”必要不充分条件，故选：B．3．（河北省石家庄市）祖暅原理也称祖氏原理，一个涉及几何求积的著名命题．内容为：“幂势既同，则积不容异”．“幂”是截面积，“势”是几何体的高．意思是两个等高的几何体，如在等高处的截面积相等，体

积相等．设A，B为两个等高的几何体，p：A、B的体积相等，q：A、B在同一高处的截面积相等．根据祖暅原理可知，p是q的（）A．充分必要条件B．充分不必要条件C．必要不充分条件D．既不充分也不必要条件【答案】C【解析】已知A，B为两个等高的几何体，由祖暅原理知qp，而p不

能推出q，可举反例，两个相同的圆锥，一个正置，一个倒置，此时两个几何体等高且体积相等，但在同一高处的截面积不相等，则p是q的必要不充分条件故选：C