【文档说明】《2023年新高考数学大一轮复习讲义之方法技巧与题型全归纳（新高考专用）》专题11 导数中的同构问题（原卷版）.docx，共(10)页，621.468 KB，由envi的店铺上传

转载请保留链接：https://www.doc5u.com/view-793798ca539c79f8d2c2976d4ef88595.html

以下为本文档部分文字说明：

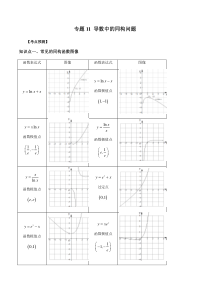
专题11导数中的同构问题【考点预测】知识点一、常见的同构函数图像函数表达式图像函数表达式图像lnyxx=+lnyxx=−函数极值点()1,1−lnyxx=函数极值点11,ee−lnxyx=函数极值点1,ee

lnxyx=函数极值点(),eexyex=+过定点()0,1xyex=−函数极值点()0,1xyxe=函数极值点11,e−−xeyx=函数极值点()1,exxye=函数极值点11,e知识点二：同构式的基本概念与导数压轴题1、同构式：是指除了变量不同，其余地方均相同的

表达式2、同构式的应用：（1）在方程中的应用：如果方程()0fa=和()0fb=呈现同构特征，则,ab可视为方程()0fx=的两个根（2）在不等式中的应用：如果不等式的两侧呈现同构特征，则可将相同的结构构造为一个函数，进

而和函数的单调性找到联系。可比较大小或解不等式。<同构小套路>①指对各一边，参数是关键；②常用“母函数”：()xfxxe=，()xfxex=；寻找“亲戚函数”是关键；③信手拈来凑同构，凑常数、x、参数；④复合函数（亲戚函数）比大小，利用单调性求参数范围.（

3）在解析几何中的应用：如果()()1122,,,AxyBxy满足的方程为同构式，则,AB为方程所表示曲线上的两点。特别的，若满足的方程是直线方程，则该方程即为直线AB的方程（4）在数列中的应用：可将递推公式变形为“依序同构”的特征，即关于(),nan与()1,1nan−−的同构式，

从而将同构式设为辅助数列便于求解3、常见的指数放缩：)1();0(1==+xexexxexx4、常见的对数放缩：)(ln);1(1ln11exexxxxxx==−−5、常见三角函数的放缩：xxxxtansin,2,0

6、学习指对数的运算性质时，曾经提到过两个这样的恒等式：（1）0a当且1,0ax时，有logaxax=（2）当0a且1a时，有logxaax=再结合指数运算和对数运算的法则，可以得到下述结论（其中0x）（3）()lnee;lnlne

xxxxxxxx+=+=（4）ln:lnlnxxxxeeexxxx−=−=（5）()22ln2ee;2lnlnexxxxxxxx+=+=（6）2ln2ln22,xxxxxxeeeexx−−==再结合常用的切线不等式lnxx-1，ln,e1,eeexxxxxx+等，可以

得到更多的结论，这里仅以第（3）条为例进行引申：（7）lneeln1xxxxxx+=++；()lnlnee1xxxxxx+=−（8）lneee(ln)xxxxxx+=+；()1lnlnxxxxexxxexee−+==【题型归纳目录】题

型一：不等式同构题型二：同构变形题型三：零点同构题型四：利用同构解决不等式恒成立问题题型五：利用同构求最值题型六：利用同构证明不等式【典例例题】题型一：不等式同构例1．（2022·陕西·西安中学模拟预测（理））已知1,,,eabc+

，且ln55lnaa=−，ln33lnbb=−，ln22lncc=−，则（）A．bcaB．cbaC．acbD．abc例2．（2022·河南焦作·三模（理））设0.02e1a=−，()0.012e1b=−，sin0

.01tan0.01c=+，则（）A．abcB．acbC．cabD．bca例3．（2022·四川·广安二中模拟预测（理））已知0πxy，且esinesinyxxy=，其中e为自然对数的底数，则下列选项中一定成立的是（）A

．cocos0sxy+B．coscos0xy+C．cossinxyD．sinsinxy题型二：同构变形例4．（2022·全国·高三专题练习）对下列不等式或方程进行同构变形，并写出相应的同构函数．(1)2log20kxxk−；(

2)21eln0xx−；(3)2lne0mxxxm−；(4)()++1e12lnaxaxxx；(5)()()ln1212exaxxax−+−+；(6)lne(1)xaxaxxx−++；(7)e2ln0

xxx−−−=；(8)2eln0xxx+=．题型三：零点同构例5．（2022·全国·高三专题练习）已知函数()e2(ln)xfxxaxx=−+有两个零点，则a的最小整数值为（）A．0B．1C．2D．3例6．（2021·全国·模拟预测）在数学中，我们把

仅有变量不同，而结构、形式相同的两个式子称为同构式，相应的方程称为同构方程，相应的不等式称为同构不等式．若关于a的方程6eeaa=和关于b的方程()31ln2ebb−−=（a，b，R）可化为同构方程，则=________，()lnab=________．例7．（2021·安徽安庆·

高三阶段练习（理））在数学中，我们把仅有变量不同，而结构､形式相同的两个式子称为同构式，相应的方程称为同构方程，相应的不等式称为同构不等式.若关于a的方程6aaee=和关于b的方程31(ln2)(,)bbeabR−−=可化为同构方程

.（1）求ab的值；（2）已知函数1()(ln)3fxxx=+.若斜率为k的直线与曲线'()yfx=相交于11(,)Axy，2212(,)()Bxyxx两点，求证：.121xxk例8．（2022·辽宁·大

连市普兰店区高级中学模拟预测）已知函数()()ln11fxxx=+−+．(1)求函数()fx的单调区间；(2)设函数()elnxgxaxa=−+，若函数()()()Fxfxgx=−有两个零点，求实数a的取值范

围．题型四：利用同构解决不等式恒成立问题例9．（2022·陕西·长安一中模拟预测（理））若对任意0x，恒有()112lnaxaxxxe++，则实数a的最小值为（）A．21eB．22eC．1eD．2e例10．（2022·河南·高三期末（理））若关于x的不

等式()()ln1exaxxaa+−R恒成立，则a的取值范围是______．例11．（2022·全国·高三专题练习）已知0，对任意的(0,)x+，不等式2ln02xxe−恒成立，则的最小值为___________.例12．（2022·全国·高三专题练习）若

关于x的不等式lnxeaxa−恒成立，则实数a的取值范围为__________．例13．（2022·全国·高三专题练习）已知不等式1lnmxxmxxe++对()1,x+恒成立，则实数m的最小值为_____

_____.例14．（2022·全国·高三专题练习）设0k，若存在正实数x，使得不等式127log30kxxk−−成立，则k的最大值为（）A．1ln3eB．ln3eC．ln3eD．ln32例15．（2022·全国·高三专题练习）已知函数2()1xfxxe=−，

不等式()lnfxmxx+对任意(0,)x+恒成立，则实数m的取值范围是（）A．(,2]−B．[0,2]C．(2,e1−−D．20,1e−例16．（2022·河南·高三阶段练习（文））若关于x的不等式()eln1exaxaxx−+−在()1,+上恒成立，则实数a的

取值范围为（）A．1,e−B．(,3−C．(,2−D．(,e−例17．（2022·全国·高三专题练习（理））已知函数2()(1)ln1(1)fxaxaxa=+++−„，对12,(0,)xx+，恒有()()12124fxfxxx−−

…，则实数a的取值范围是（）A．2(,e]−−B．(,e]−−C．[2,1]−−D．(,2]−−例18．（2022·全国·高三专题练习（理））已知函数()4elnxfxkxx=−，当1x时，不等式()1fxx+恒成立，则k的

取值范围是（）A．(,e−−B．(,4−−C．(2,e−−D．(,0−例19．（2022·安徽亳州·高三期末（理））已知0a，若1x时，elnelnxxaaxx−−−−恒成立，则a的最小值为（）A．1−B．2−

C．e−D．2e−例20．（2022·安徽合肥·高三期末（理））若不等式()eln110xaax−−+对1,12x恒成立（e为自然对数的底数），则实数a的最大值为（）A．e1+B．eC．2e1+D．2e例21.（2022·全国·高三专题练习）已

知不等式1lneaxxaxx++对()1x+，恒成立，则实数a的最小值为（）A．e−B．e2−C．e−D．2e−题型五：利用同构求最值例22．（2022·全国·高三专题练习）已知函数()()ln

1fxxx=+−，()lngxxx=，若()112lnfxt=+，()22gxt=，则()122lnxxxt−的最小值为（）．A．21eB．2eC．12e−D．1e−例23．（2022·全国·高三专题练习（理））设大于1的两个实数a，b满足22lnanbbea，则正

整数n的最大值为（）．A．7B．9C．11D．12题型六：利用同构证明不等式例24．（2022·福建南平·三模）已知函数()lnmfxxx=+.(1)讨论函数()fx的单调性；(2)若114em，求证：函数()elnmxxxgxxm−=+有两个零点1x，2x且12112exx+.例

25．（2022·四川眉山·三模（文））已知函数()()ee0xfxxx=−.(1)求()fx的单调区间；(2)证明：当ex时，()elnlnlnlnxxxx−.例26．（2022·河北·高三阶段练习）已知函数()lnfxxx=．(1)讨论()fx的单调性；(2)设a，

b为两个不相等的正数，且baab=，证明：2111eab+．例27．（2022·河南郑州·二模（文））已知函数()e21exfxx=−+，()ln2xgxx=+.(1)求函数()gx的极值；(2)当x>0时，证明：()()fxgx例28．（2022·河南省

浚县第一中学模拟预测（理））已知函数()()exfxaxa=−R．(1)讨论f(x)的单调性．(2)若a＝0，证明：对任意的x>1，都有()4333lnfxxxxx−+．