【文档说明】《2023年新高考数学大一轮复习讲义之方法技巧与题型全归纳（新高考专用）》专题40 抛物线及其性质（原卷版）.docx，共(19)页，1.299 MB，由envi的店铺上传

转载请保留链接：https://www.doc5u.com/view-581b5f929ecf980c3bb70ab42bb189b1.html

以下为本文档部分文字说明：

专题40抛物线及其性质【考点预测】知识点一、抛物线的定义平面内与一个定点F和一条定直线()lFl的距离相等的点的轨迹叫做抛物线，定点F叫抛物线的焦点，定直线l叫做抛物线的准线．注：若在定义中有Fl，则动点的轨迹为l的垂线，垂足为点F．知识点

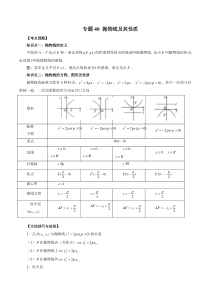
二、抛物线的方程、图形及性质抛物线的标准方程有4种形式：22ypx=，22ypx=−，22xpy=，22(0)xpyp=−，其中一次项与对称轴一致，一次项系数的符号决定开口方向图形标准方程22(0)ypxp=22(0)ypxp=−22(0)xpy

p=22(0)xpyp=−顶点(00)O，范围0x，yR0x，yR0y，xR0y，xR对称轴x轴y轴焦点(0)2pF，(0)2pF−，(0)2pF，(0)2pF−，离心率1e=准线方程2px=−2px=2py=−2py=焦半径11()Axy，12pAFx=+12pAFx=−+

12pAFy=+12pAFy=−+【方法技巧与总结】1、点00(,)Pxy与抛物线22(0)ypxp=的关系（1）P在抛物线内（含焦点）2002ypx．（2）P在抛物线上2002ypx=．（3）P在抛物线外2002ypx

．2、焦半径抛物线上的点00(,)Pxy与焦点F的距离称为焦半径，若22(0)ypxp=，则焦半径02pPFx=+，max2pPF=．3、(0)pp的几何意义p为焦点F到准线l的距离，即焦准距，p越大，抛物线开口越大．4、焦点弦若AB为抛物线

22(0)ypxp=的焦点弦，11(,)Axy，22(,)Bxy，则有以下结论：（1）2124pxx=．（2）212yyp=−．（3）焦点弦长公式1：12ABxxp=++，12122xxxxp+=，当12xx=时，焦点弦取最小值2p，即所

有焦点弦中通径最短，其长度为2p．焦点弦长公式2：22sinpAB=（为直线AB与对称轴的夹角）．（4）AOB的面积公式：22sinAOBpS=（为直线AB与对称轴的夹角）．5、抛物线的弦若AB为抛物线22(p0)ypx=

的任意一条弦，1122(,),(,)AxyBxy，弦的中点为000(,)(0)Mxyy，则（1）弦长公式：212122111(0)ABABkxxyykkk=+−=+−=（2）0ABpky=（3）直线AB的

方程为000()pyyxxy−=−（4）线段AB的垂直平分线方程为000()yyyxxp−=−−6、求抛物线标准方程的焦点和准线的快速方法（4A法）（1）2(0)yAxA=焦点为(,0)4A，准线为4Ax=−（2）2(0)xAyA=焦

点为(0,)4A，准线为4Ay=−如24yx=，即24yx=，焦点为1(0,)16，准线方程为116y=−7、参数方程22(0)ypxp=的参数方程为222xptypt==（参数tR）8、切线方

程和切点弦方程抛物线22(0)ypxp=的切线方程为00()yypxx=+，00(,)xy为切点切点弦方程为00()yypxx=+，点00(,)xy在抛物线外与中点弦平行的直线为00()yypxx=+，此直线与抛物线相离，点00(,)xy（含

焦点）是弦AB的中点，中点弦AB的斜率与这条直线的斜率相等，用点差法也可以得到同样的结果．9、抛物线的通径过焦点且垂直于抛物线对称轴的弦叫做抛物线的通径．对于抛物线22(0)ypxp=，由()2pAp，，()2pBp−，，可得||2ABp=，故

抛物线的通径长为2p．10、弦的中点坐标与弦所在直线的斜率的关系：0pyk=11、焦点弦的常考性质已知11()Axy，、22()Bxy，是过抛物线22(0)ypxp=焦点F的弦，M是AB的中点，l是抛物线的准线，MNl⊥，N为垂足．（

1）以AB为直径的圆必与准线l相切，以AF（或BF）为直径的圆与y轴相切；（2）FNAB⊥，FCFD⊥（3）2124pxx=；212yyp=−（4）设BDl⊥，D为垂足，则A、O、D三点在一条直线上【题型归纳目录】题型一：抛物线的定义与方程题型二：抛

物线的轨迹方程题型三：与抛物线有关的距离和最值问题题型四：抛物线中三角形，四边形的面积问题题型五：焦半径问题题型六：抛物线的性质xyBFACDNMO【典例例题】题型一：抛物线的定义与方程例1．（2022·黑龙江·佳木斯一中三

模（理））已知抛物线22(0)xpyp=的焦点为F，准线为l，过点F且倾斜角为30°的直线交抛物线于点M（M在第一象限），MNl⊥，垂足为N，直线NF交x轴于点D，若||23MD=，则抛物线的方程是（）A．2xy=B．22xy=C．24xy

=D．28xy=【方法技巧与总结】求抛物线的标准方程的步骤为：（1）先根据题设条件及抛物线定义判断它为抛物线并确定焦点位置：（2）根据题目条件列出P的方程（3）解方程求出P，即得标准方程例2．（2022·全国·高

三专题练习）顶点在原点，关于x轴对称，并且经过点()1,2M−的抛物线方程为________.例3．（2022·湖南·高三开学考试）已知抛物线的焦点F在x轴上，直线2y=−与抛物线交于点A，且52AF=.写出抛物线的一个标准方程___________.例4

．（2022·全国·高三专题练习）点(5,3)M到抛物线2yax=的准线的距离为6，那么抛物线的标准方程是（）A．2112xy=B．2112xy=或2136xy=−C．2136xy=−D．212xy=或236xy=−例5．（2022·河南·洛宁县第一高级中学一模（文））已知点F是拋物线()2:20

Cxpyp=的焦点，()0,1Px是C上的一点，4PF=，则p=（）A．2B．4C．6D．8例6．（2022·北京·高三开学考试）抛物线W：24yx=的焦点为F.对于W上一点P，若P到直线5x=的距离是P到点F距离的2倍，则点P的

横坐标为（）A．1B．2C．3D．4例7．（2022·全国·高三专题练习）以x轴为对称轴，顶点为坐标原点，焦点到准线的距离为4的抛物线方程是（）A．28yx=B．28yx=−C．28yx=或28yx=−D．28xy=或28x

y=-例8．（2022·全国·高三专题练习）顶点在原点，焦点在x轴上，过焦点作垂直于x轴的直线交抛物线于A，B两点，AB的长为8，求抛物线的方程．题型二：抛物线的轨迹方程例9．（2022·上海市复兴高级中学高三开学考试）在平面上，到点()1,0A的距离等

于到直线23xy+=的距离的动点P的轨迹是（）A．直线B．圆C．椭圆D．抛物线【方法技巧与总结】常见考题中，会让我们利用圆锥曲线的定义求解点P的轨迹方程，这时候要注意把动点P和满足焦点标志的定点连起来做判断．焦点往往有以下的特征：（1）关于坐标轴对称

的点；（2）标记为F的点；（3）圆心；（4）题上提到的定点等等．当看到满足以上的标志的时候要想到曲线的定义，把曲线和满足焦点特征的点连起来结合曲线定义判断．注意：在求解轨迹方程的题中，要注意x和y的取值范围.例10．（2022·全国·高三专题练习）已知点(2,2)M，直线:10lxy

−−=，若动点P到l的距离等于PM，则点P的轨迹是（）A．椭圆B．双曲线C．抛物线D．直线例11．（2022·全国·高三专题练习）若动点(,)Mxy满足()()225123412xyxy−+−=−+，则点M的轨迹是（）A．圆B．椭圆C．双曲线D．抛物线例12．（2022·全国·高三专题练习）在平

面直角坐标系xOy中，动点(),Pxy到直线1x=的距离比它到定点()2,0−的距离小1，则P的轨迹方程为（）A．22yx=B．24yx=C．24yx=−D．28yx=−例13．（2022·全国·高三专题练习（理））已知点()1,0A−､()10B,，若过A､B两点的动抛物线的准

线始终与圆228xy+=相切，该抛物线焦点的轨迹是某圆锥曲线的一部分，则该圆锥曲线是（）A．椭圆B．圆C．双曲线D．抛物线例14．（2022·全国·高三专题练习）已知动圆M与直线y=2相切，且与定圆2231()Cxy=：＋＋外切，则动圆圆心M的轨迹方程为（）A．212xy=−B．212xy=C．

212yx=D．212yx=−例15．（2022·全国·高三专题练习）斜线段AB与平面所成的角为15，平面内的动点P满足15PAB=，则点P的轨迹是（）A．圆B．椭圆C．抛物线D．双曲线的一支例

16．（多选题）（2022·江苏南京·高三阶段练习）已知直线:10lx+=，点()1,0P，圆心为M的动圆经过点P，且与直线l相切，则（）A．点M的轨迹为抛物线B．圆M面积最小值为4C．当圆M被y轴截得的弦长为25时，圆M的半径为3D．存在点M，使得233MOMP=，其中O为坐标

原点例17．（2022·全国·高三专题练习）与点()0,3F−和直线30y−=的距离相等的点的轨迹方程是______．例18．（2022·全国·高三专题练习）已知动点(),Mxy的坐标满足()2222−+=+xyx，则动点M的轨迹方程为

_____________．例19．（2022·湖北·荆州中学高三开学考试）已知动点(,)Mxy到定点(1,0)F与定直线0x=的距离的差为1．则动点M的轨迹方程为________．例20．（多选题）（2022·全国·高三

专题练习）已知定圆A的半径为1，圆心A到定直线l的距离为d，动圆C与圆A和直线l都相切，圆心C的轨迹为如图所示的两条抛物线，记这两抛物线的焦点到对应准线的距离分别为1p，2p，则（）A．1dB．12ppd+=C．212ppd=D．12112ppd+例21．（2022

·全国·高三专题练习）动点(),Mxy到y轴的距离比它到定点()2,0的距离小2，求动点(),Mxy的轨迹方程．题型三：与抛物线有关的距离和最值问题例22．（2022·全国·高三专题练习）已知(),Pmn为抛物线C：

216yx=上一动点，过C的焦点F作P：()()221xmyn−+−=的切线，切点为A，则线段FA长度的最小值为（）A．3B．15C．7D．37【方法技巧与总结】抛物线上任意一点到焦点的距离等于到准线的距离

，利用这一定义可以把相等长度的线段进行转化，从而把两条线段长度之和的问题转化为两点间的距离问题或点到直线的距离问题，即在解题中掌握“抛物线的定义及其性质”，若求抛物线上的点到定直线（并非准线）距离的最值问题用参数法或切线法求解。例23．（2022·吉林·东北师

大附中模拟预测（文））抛物线24yx=上任意一点P到点()5,0M的距离最小值为___________.例24．（2022·全国·高三专题练习）已知M为抛物线24yx=上的动点，F为抛物线的焦点，()3,1P，则MPMF+的最小值为___________.例25．（20

22·全国·高三专题练习）若抛物线2:2(0)Cypxp=上一点(5,)t到焦点的距离为6，P、Q分别为抛物线与圆22(6)1xy−+=上的动点，则PQ的最小值为______．例26．（2022·全国

·高三专题练习）已知P为抛物线24yx=上的一个动点，Q为圆()2241xy+−=上的一个动点，那么点P到点Q的距离与点P到抛物线准线的距离之和的最小值是______.例27．（2022·宁夏·吴忠中学三模（文））已知抛物线2:2(0)Cypxp=上一点00(,)Pxy到y轴的距离与到点(0

,4)Q的距离之和的最小值为2，则实数p的值为_____，例28．（2022·全国·高三专题练习）已知F为抛物线22yx=的焦点，()00,Axy为抛物线上的动点，点()1,0B−.则221ABAF+最大值为_______.例29．（2022·辽宁朝阳·高三阶段练习

）已知F为抛物线216yx=的焦点，P为抛物线上的动点，点()2,0A−，则2193PAPF+−的最小值为______．例30．（2022·全国·高三专题练习）已知抛物线216yx=的焦点为F，P点在抛物线上

，Q点在圆()()22:624Cxy−+−=上，则PQPF+的最小值为（）A．4B．6C．8D．10例31．（2022·广西桂林·高三开学考试（理））已知，点P是抛物线2:4Cyx=上的动点，过点P向y轴作垂线，垂足记为点N，点(3,4)M，则||||PMPN+的最小值是（）A．

251−B．51−C．51+D．251+例32．（2022·全国·高三专题练习）已知A()4,2−，F为抛物线28yx=的焦点，点M在抛物线上移动，当MAMF+取最小值时，点M的坐标为（）A．()0,0B．()1,22−C．()2,2−D．1,22−例33．（2022·上海市向明

中学高三开学考试）设抛物线2:8Cxy=的焦点为F，准线为l，()00,Pxy为C上一动点，(2,1)A，则下列结论错误的是（）A．当04x=时，||PF的值为6B．当02x=时，抛物线C在点P处的切线方程为220xy−−=C．||||PAPF+的最小值为3D．||||PAPF−的最大值为5例34

．（2022·云南民族大学附属中学模拟预测（理））已知点P为抛物线24yx=−上的动点，设点P到2:1lx=的距离为1d，到直线40xy+−=的距离为2d，则12dd+的最小值是（）A．52B．522C．2D．2例35．（2022·全国·高三专题练习）已知过抛物线2:4Cyx=的焦点F且倾斜角

为60的直线交C于,AB两点（A在B的右边），P为C上一点，58ABQB=，则PFPQ+的最小值为（）A．3B．113C．133D．5例36．（2022·全国·高三专题练习）已知定点(3,3)M−，点P为拋物线2:4Cxy=上一动点，P到x轴的距离为d，

则||dPM+的最小值为（）A．4B．5C．131−D．13例37．（多选题）（2022·全国·高三专题练习）已知A（a，0），M（3，-2），点P在抛物线24yx=上，则（）A．当1a=时，PA最小值为1B．当3a=时，PA的最小值为3C．当1a=时，PAPM

+的最小值为4D．当3a=时，PAPM−的最大值为2例38．（多选题）（2022·全国·高三专题练习）已知F是抛物线24yx=的焦点，P是抛物线24yx=上一动点，Q是()()22:411Cxy−+−=

上一动点，则下列说法正确的有（）A．PF的最小值为1B．QF的最小值为10C．PFPQ+的最小值为4D．PFPQ+的最小值为101+例39．（多选题）（2022·江苏·南京市第一中学高三阶段练习）已知抛物线2:4Cyx=，圆221:(1)(4FxyF−+=为圆心），点P在抛物线

C上，点Q在圆F上，点(1,0)A−，则下列结论中正确的是（）A．||PQ的最小值是12B．||||PFPA的最小值是22C．当PAQ最大时，152AQ=D．当PAQ最小时，152AQ=例40．（2022·江苏·南京市金陵中学河西分校高三阶段练习）P是抛物线28y

x=上的动点，P到y轴的距离为1d，到圆22:(3)(3)4Cxy++−=上动点Q的距离为2d，则12dd+的最小值为________．题型四：抛物线中三角形，四边形的面积问题例41．（2022·贵州贵阳·高三开学考试（理））已知抛物线2:2Cyx=的焦点为,(

,)FAmn是抛物线C上的一点，若52AF=，则OAF△(O为坐标原点)的面积是（）A．12B．1C．2D．4【方法技巧与总结】解决此类问题经常利用抛物线的定义，将抛物线上的点焦点的距离转化为到准线的距离，并构成直角三角形或直角梯形，从而计算其面积或面积之比。例42．（2

022·河南·高三开学考试（文））已知倾斜角为60的直线l过抛物线2:2(0)Cypxp=的焦点F，且与C交于AB，两点（点A在第一象限），若3AF=，则BF=______．例43．（2022·全国·高三专题练习）设抛物线242yx=的焦点为F，准线为l，过抛物线

上一点A作l的垂线，垂足为B．设(42,0)C，AF与BC相交于点D．若||||CFAF=，则ACD△的面积为__________．例44．（2022·全国·高三专题练习）设抛物线2:2(0)Cypxp=的焦点为F，准线l与x轴

的交点为K，点A在C上，已知点A的横坐标为2，22AF=，则AKF的面积AKFS=___________.例45．（2022·全国·高三专题练习）已知抛物线24yx=的焦点为F，过点F的直线交拋物线于A、B两点，延长FB交准线于点C，分别过点A、B作

准线的垂线，垂足分别记为M、N，若2BCBN=，则AFM△的面积为________.例46．（2022·全国·高三专题练习）如图，已知点F为抛物线2:4Cyx=的焦点过点F且斜率存在的直线交抛物线C于A，B两点，点D为准线l与x轴的交点，则DAB的面积S的取值范围为______．例47．（20

22·安徽·芜湖一中模拟预测）已知抛物线28yx=的焦点为F，过点F的直线交抛物线于A，B两点，延长FB交准线于点C，分别过点A，B作准线的垂线，垂足分别记为M，N，若||2||BCBN=，则AFM△的面积

为_______．例48．（2022·安徽省定远县第三中学高三阶段练习）已知抛物线2:2(0)Cypxp=的焦点是F，A是C的准线上一点，线段AF与C交于点B，与y轴交于点D，且||5||ABBF=，4DOFS=△（O为原点），则C的方程为___________.例49．（多选题）（2022·河

北廊坊·高三开学考试）已知抛物线C：()220ypxp=的焦点为()1,0F，坐标原点为O，直线l与抛物线C交于A，B两点（与O均不重合），以线段AB为直径的圆过原点O，则AOB与AOF的面积之和可能为（）A．17B．85C．18D．93例50．（多选题）（2022·云南大理·模拟预测）设点F

为抛物线C：()220ypxp=的焦点，过点F斜率为k的直线l与抛物线C交于,MN两点（点M在第一象限），直线l交抛物线C的准线于点P，若34MFFN==，则下列说法正确的是（）A．4p=B．0FPFM+=C．3k=D．MON△的面积为43（O为坐标原点）例51．（202

2·甘肃·永昌县第一高级中学高三阶段练习（文））已知F为抛物线2:8Cyx=的焦点，点A为C上一点，点B的坐标为()6,0，若AFBF=，则ABF的面积为（）A．2B．4C．8D．16例52．（2022·

云南师大附中高三阶段练习）已知M是抛物线2:4Cxy=上一点，F为抛物线的焦点，点()0,2N−，若MFNF=，则MFN△的面积为（）A．22B．23C．32D．33例53．（2022·山西运城·高三阶段练习（文））过点P作抛物线2:4Cxy=的切线12,ll，切点分别为,MN，若PMN的重心坐

标为(3,4)，则P点坐标为（）A．(3,3)−B．(1,2)C．(2,1)D．()3,3−题型五：焦半径问题例54．（2022·云南·高三阶段练习）已知抛物线2:4Dyx=的焦点为F，准线为l，点P在D上，过点P作准线l的垂线，垂足为A，若PAAF=，则

PF=（）A．2B．22C．23D．4【方法技巧与总结】（1）||||1cos1cosppAFBF==−+；．（2）1222||sinpABxxpa=++=．（3）22sinAOBpS△=．例55．（20

22·全国·高三专题练习）过抛物线22(0)ypxp=的焦点F的直线交抛物线于点A，B，交其准线于点C，若2,3CBBFAF==，则此抛物线方程为__________．例56．（2022·广东·高三阶段练习）已

知抛物线2:4Cyx=的焦点为F，点A，B是抛物线C上不同两点，且A，B中点的横坐标为2，则||||+=AFBF（）A．4B．5C．6D．8例57．（2022·全国·高三专题练习（文））已知抛物线C：()220ypxp=的焦点为1,04F，A00(,)xy是C上一点

，|AF|=054x，则0x=（）A．1B．2C．4D．8例58．（2022·全国·高三专题练习）如图，已知抛物线1C的顶点在坐标原点，焦点在x轴上，且过点()1,4，圆222:8120Cxyx+−+=，过圆心2C的直

线l与抛物线和圆分别交于点P，Q，M，N，则4PMQN+的最小值为（）A．23B．26C．36D．62例59．（2022·河南·模拟预测（文））设抛物线2:2(0)Cypxp=的焦点为F，点A、B在抛物线上

，若AFx⊥轴，且2BFAF=，则AFB=（）A．6或5π6B．π3或2π3C．π4或34D．π2例60．（2022·广东汕头·高三阶段练习）已知ABC的三个顶点都在抛物线24yx=上，F为抛物线的焦点，若()13AFABAC=+，则

||||||++=AFBFCF（）A．3B．6C．9D．12例61．（2022·江西·高三开学考试（理））已知抛物线232xy=的焦点为F，抛物线上一点A满足10AF=，则直线AF的斜率为（）A．34−B．34C．34D．2例62．（2022·江

西·高三阶段练习（文））已知抛物线2:2(0)Cypxp=的焦点F到其准线的距离为2，过焦点F的直线l与抛物线C交于A、B两点，则||2||AFBF+的最小值为（）A．223+B．823+C．178D

．9例63．（2022·河南·商丘市第一高级中学高三开学考试（文））已知抛物线C：22ypx=的焦点为(1,0)F，准线与x轴交于点A，点M在第一象限且在抛物线C上，则当AMFM取最大值时，直线AM方程为（）A．21yx=+B．21yx=−C．1yx=+D．1yx=−例64

．（多选题）（2022·重庆八中高三阶段练习）已知O为坐标原点，P为y轴上的动点，过抛物线2:2(0)Cypxp=焦点F的直线与C交于,AB两点，其中A在第一象限，(2,0)Qp，若||||AFQF=，则（）A．||||QAQFB．|

|||BFOB=C．当0PAPB=时，P的纵坐标一定大于24pD．不存在P使得2PAPBp=−例65．（多选题）（2022·湖南师大附中高三阶段练习）已知,AB是抛物线2:4Cyx=上两动点，F为抛物线C的焦点，则（）A．直线AB过

焦点F时，AB最小值为4B．直线AB过焦点F且倾斜角为60时（点A在第一象限），2AFBF=C．若AB中点M的横坐标为3，则AB最大值为8D．点A坐标()4,4，且直线,AFAB斜率之和为0,AF与抛物线的另一交点为D，则直线，BD方程为：4870xy++=例66．（2022·全

国·成都七中高三开学考试（理））设F是抛物线24Cyx=：的焦点，点A在抛物线C上，()30B，，若2AFBF=，则AB=____________.例67．（2022·全国·高三专题练习）已知抛物线()2:20Cypxp=的焦点为F，点A是抛物线C的准线与坐标轴的交点，点P在抛物线C上，若3

sin5PAF=，则sinPFA=__________.例68．（2022·全国·高三专题练习）过抛物线2ypx=，()0p的焦点F作直线l，交抛物线于A，B两点，若3FAFB=，则直线l的倾斜角等于__________.题型六：抛物线的性质例69．（2022·湖南·新邵县教研室

高三期末（文））已知抛物线24yx=的焦点为F，过点F且倾斜角为45的直线l与抛物线分别交于AB､两点，则AB=（）A．1B．3C．6D．8【方法技巧与总结】在处理抛物线的考题的时候，要更加注意定义优先原则，考察频率更高，很多问题用上抛物线定义可以简化计算．例70．（多选题）（

2022·全国·高三专题练习）关于抛物线22yx=−，下列说法正确的是（）A．开口向左B．焦点坐标为()1,0−C．准线为1x=D．对称轴为x轴例71．（2022·江西·高三阶段练习（文））若抛物线28xy=上一点P到焦点的距离为6，则点P到x轴的距离为____________．例72．

（2022·四川省南充市白塔中学高三阶段练习（理））已知点F是抛物线2:2(0)Eypxp=的焦点，O为坐标原点，A，B是抛物线E上的两点，满足||||10,0FAFBFAFBFO+=++=，则p=______．例73．（2022·江西南昌·模拟预测（文

））抛物线22yx=的焦点到准线的距离为（）A．4B．2C．1D．12例74．（2022·全国·高三专题练习）下列四个抛物线中，开口朝下且焦点到准线的距离为5的是（）A．210yx=−B．210xy=−C．25yx=−D．25xy=−例75．（2022·湖北十堰·三模）下列四个抛物线中，

开口朝左的是（）A．25yx=B．25xy=−C．25yx=−D．25xy=例76．（2022·江西南昌·高三阶段练习）若抛物线22(0)ypxp=上的点(1,)Pa到焦点的距离比到直线4x=−的距离小1，则a=（）A．112B．26C．6D．23例77．（2022·全国

·高三专题练习）对抛物线218yx=，下列描述正确的是（）A．开口向上，焦点为()02，B．开口向上，焦点为1032，C．开口向右，焦点为()20，D．开口向右，焦点为1032，例78．（

2022·青海·大通回族土族自治县教学研究室高三开学考试（理））抛物线C：()220ypxp=的焦点为F，准线l交x轴于点()2,0Q−，过焦点的直线m与抛物线C交于A，B两点，则（）A．2p=B．10AB≥C．直线AQ与BQ的斜率之和为0D

．准线l上存在点M，若MAB△为等边三角形，可得直线AB的斜率为例79．（2022·江西·高三阶段练习（理））已知抛物线2:2(0)Cypxp=的焦点为F，点F到直线:230lxy−−=的距离为55，则p的值为_________

____．例80．（2022·河北邯郸·高三开学考试）若抛物线24yx=的准线与圆22:()1Cxay−+=相切，则=a___________.例81．（2022·广东深圳·高三阶段练习）已知点F为抛物线2:8Cxy=的焦点，经过点F的

直线l交C于,AB两点，交x轴于点E，若EBBF=，则点A的纵坐标为___________.例82．（2022·全国·高三专题练习）抛物线2yax=的准线方程是1y=，则实数=a___________.例83．（2022·全国·高三专题练习）已知抛物线()220ypxp=，F为其焦点，l

为其准线，过F任作一条直线交抛物线于AB，两点，','AB分别为AB，在l上的射影，M为''AB的中点，给出下列命题：①''AFBF⊥；②AMBM⊥；③'AF//BM；④'AF与AM的交点在y轴上；⑤'AB与'AB交于原点.其中真命题是__________．（写

出所有真命题的序号）例84．（2022·安徽省太和中学高三阶段练习）在平面直角坐标系xOy中，0r，⊙M：()22234rxry−+=与抛物线C：24yx=有且仅有两个公共点，直线l过圆心M且交抛物线C于A，B两点，则OAOB=______．例85．（2022·全国·高三专题练习）已知直线l过

抛物线C：22ypx=（0p）的焦点，且与抛物线C交于A，B两点，若使2AB=的直线l有且仅有1条，则p=______.【过关测试】一、单选题1．（2022·河南·宝丰县第一高级中学高三开学考试（理））已

知抛物线2:4Cyx=的焦点为F，准线为l，与x轴平行的直线与l和C分别交于A，B两点，且若AFBF=，则AB=（）A．2B．22C．23D．42．（2022·安徽·高三开学考试）已知点M在抛物线2:2(0)Cypxp=上，若以点M

为圆心半径为5的圆与抛物线C的准线相切，且与x轴相交的弦长为6，则p=（）A．2B．8C．2或8D．63．（2022·安徽·高三开学考试）设抛物线2112yx=上一点P到x轴的距离是1，则点P到该抛物线焦点的距离是（）A．3B．4C．7D．134．（2022·河南·上蔡县

衡水实验中学高三阶段练习（文））直线1yx=−过抛物线2:2(0)Cypxp=的焦点F，且与C交于AB、两点，则||AB=（）A．6B．8C．2D．45．（2022·陕西·西乡县教学研究室一模（文））已知过抛物线2:4Cyx=的

焦点F且倾斜角为60的直线交C于A，B两点，Q为AB的中点，P为C上一点，则||||PFPQ+的最小值为（）A．83B．53C．8D．56．（2022·福建师大附中高三阶段练习）设抛物线24xy=的焦点为

F，若222:(4)(0)Mxyrr+−=与抛物线有四个不同的交点，记y轴同侧的两个交点为,AB，则||||FAFB的取值范围是（）A．(0,4)B．(5,9)C．(0,9)D．(4,9)7．（2022·

广东广东·高三阶段练习）在曲线2yx=上有两个动点,,(1,0)PQE，且满足EPEQ⊥，则EPQP的最小值为（）A．14B．12C．34D．18．（2022·山东师范大学附中高三期中）抛物线C：24yx=的焦点为F，P

是其上一动点，点()1,1M，直线l与抛物线C相交于A，B两点，下列结论正确的是（）A．PMPF+的最小值是2B．动点P到点()3,0H的距离最小值为3C．存在直线l，使得A，B两点关于直线30xy+−=对称D．与抛物

线C分别相切于A、B两点的两条切线交于点N，若直线AB过定点(2,0)，则点N在抛物线C的准线上二、多选题9．（2022·全国·高三专题练习）在平面直角坐标系xOy中，已知抛物线2:4Cyx=的焦点为F，点P在抛物线C上，5,04A−，若PAF△

为等腰三角形，则直线AP的斜率可能为（）A．427B．255−C．52D．223−10．（2022·湖北·荆州中学模拟预测）已知(),Pxy为曲线2xy=上一动点，则（）A．22(1)xy+−的最小值为2B．

P到直线2yx=−−的距离的最小值为2C．2222(1)(1)(5)xyxy+−+−+−的最小值为6D．存在一个定点和一条定直线，使得P到定点的距离等于P到定直线的距离11．（2022·全国·高三专题练习

）已知抛物线C：24yx=的焦点为F，P为抛物线上一点，则下列结论正确的有（）A．焦点F到抛物线准线的距离为2B．若2PF=，则点P的坐标为()1,2C．过焦点F且垂直于x轴的直线被抛物线所截得的弦长为2D．若点M的坐标为()1,4，则PMPF+的最小值为412．（2022·重庆八中高三阶段练习）

已知抛物线2:4Cxy=的焦点为F，O为坐标原点，点()00,Mxy在抛物线C上，若5MF=，则（）A．F的坐标为()1,0B．04y=C．04x=D．42OM=三、填空题13．（2022·广东·开平市忠源纪念中学高三阶段练习）已知F是抛物线2:16Cyx=的焦点，M是C上一点，

FM的延长线交y轴于点N，若32FMMN=，则FN=___________.14．（2022·全国·高三专题练习）设过抛物线焦点F的弦为PQ，则以PQ为直径的圆与抛物线的准线的位置关系是______．15．（2022·河南省叶县高级中学模拟预测（文））已知抛物线2:4Cyx=的焦点为

F，准线为l，与x轴平行的直线与l和C分别交于A，B两点，若AFBF=，则AB=______.16．（2022·四川·成都七中高三开学考试（文））已知抛物线2:4Exy=的准线交y轴于点M，过点M作斜率为(0)k

k的直线l交E于,AB两点，且2MAMB=，则直线l的斜率是__________.四、解答题17．（2022·内蒙古包头·高三开学考试（文））已知抛物线C的顶点在原点，焦点F在y轴上，且C经过点(2,1)A，过F且斜率为(0)kk的直线l与C交于M，N两点，8MN=．

(1)求C和l的方程；(2)求过点M，N且与C的准线相切的圆的方程．18．（2022·全国·高三专题练习）已知点23,2Ppp−在抛物线()2:20Cxpyp=上.(1)求抛物线C的方程；(2)过点()0,1M的直线l交抛物线C于A，B两点，设直线OA，OB的斜率分别为1k

，2k，O为坐标原点，求证：12kk为定值.19．（2022·全国·高三专题练习）已知抛物线2:2(0)Eypxp=的焦点为F，直线xn=与抛物线E交于,AB两点，当36n=时，(OABO为坐标原点）是等边三角形.(1)求抛物线E的方程.(2)延长AF交抛物线E于点C，试问

直线BC是否恒过点D？若是，求出点D的坐标；若不是，请说明理由.20．（2022·全国·高三专题练习（理））已知抛物线22(0)ypxp=的焦点为F，点M是抛物线的准线2x=−上的动点．(1)求p的值和抛物线的焦点坐标；(2)设直线l与抛物线相交于A、B两点，且,MFABAFMB⊥⊥，求直线

l在x轴上截距b的取值范围．