 DOC
DOC
【文档说明】《2022-2023学年八年级数学上册全等三角形模型图析高分突破(人教版)》全等变化模型八 手拉手模型(解析版).docx,共(16)页,4.265 MB,由envi的店铺上传
转载请保留链接:https://www.doc5u.com/view-f0c1df0e3ab75834b685adbd61271ecd.html
以下为本文档部分文字说明:
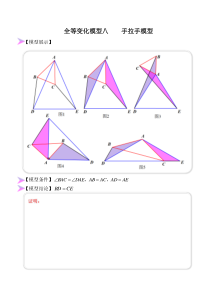
全等变化模型八手拉手模型【模型展示】【模型条件】AEADACABDAEBAC===,,【模型结论】CEBD=证明:【模型应用】如下图所示:三点共线、、,且和等边等边△,DCACDEABC(1)、AD=BE(2)、∠AC
B=∠AOB(3)、△PCQ为等边三角形(4)、PQ∥AE(5)、AP=BQ(6)、CO平分∠AOE(7)、OA=OB+OC(8)、OE=OC+OD请对以上结论(5)、结论(6)结论(7)进行证明。证明:【模型巩固】【例8-1】如图,在等腰△ABC中,BA=BC,点F在A
B边上,延长CF交AD于点E,BD=BE,∠ABC=∠DBE.(1)求证:AD=CE;(2)若∠ABC=30°,∠AFC=45°,求∠EAC的度数.【解答】(1)证明:∵∠ABC=∠DBE,∴∠ABC+∠ABE=∠DBE+∠ABE,∴∠ABD=∠CB
E.在△ADB和△CEB中,,∴△ADB≌△CEB(SAS),∴AD=CE;(2)解:∵BA=BC,∠ABC=30°,∴∠BAC=∠BCA=(180°﹣30°)=75°,∵∠AFC=45°,∴∠BCE=∠AFC﹣∠ABC=45°﹣30°=15°,∵△ADB≌△CEB,∴
∠BAD=∠BCE=15°,∴∠EAC=∠BAD+∠BAC=15°+75°=90°.【例8-2】如图,已知△ABC为等边三角形,D为BC延长线上的一点,CE平分∠ACD,CE=BD,求证:(1)△ABD≌△ACE;(2)试判断△ADE的形状,并证明.【解答】(1)
证明:∵△ABC为等边三角形,∴∠B=∠ACB=60°,AB=AC,∴∠ACD=120°,∵CE平分∠ACD,∴∠ACE=∠DCE=60°,∴∠B=∠ACE,在△ABD和△ACE中,,∴△ABD≌△ACE(SAS);(2)解:△ADE是等边三角形,证明如下:由(1)得:△ABD≌△ACE,∴AD
=AE,∠BAD=∠CAE,即∠BAC+∠CAD=∠DAE+∠CAD,∴∠DAE=∠BAC=60°,∴△ADE为等边三角形.【例8-3】如图,CA=CB,CD=CE,∠ACB=∠DCE=α,AD、BE交于点H,连CH.(1)求证:△ACD≌△BCE;(2)求证
:CH平分∠AHE;(3)求∠CHE的度数.(用含α的式子表示)【解答】(1)证明:∵∠ACB=∠DCE=α,∴∠ACD=∠BCE,在△ACD和△BCE中,,∴△ACD≌△BCE(SAS);(2)证明:过点C作CM⊥
AD于M,CN⊥BE于N,∵△ACD≌△BCE,∴∠CAM=∠CBN,在△ACM和△BCN中,,∴△ACM≌△BCN(AAS),∴CM=CN,∴CH平分∠AHE;(3)∵△ACD≌△BCE,∴∠CAD=
∠CBE,∴∠AHB=∠ACB=α,∴∠AHE=180°﹣α,∴∠CHE=∠AHE=90°﹣α.【例8-4】如图1,点M为直线AB上一动点,PAB,PMN都是等边三角形,连接BN(1)求证:AMBN=;(2)分别写出点M在如图2和图3所示位置时,线段AB、B
M、BN三者之间的数量关系(不需证明);(3)如图4,当BMAB=时,证明:MNAB⊥.【解答】(1)证明:PAB和PMN是等边三角形,60BPAMPN==,ABBPAP==,PMPNMN==,BPAMPBMPNMPB−=−,APMBPN=.
在APMPBN中APPBAPMBPNPMPN===,()APMPBNSAS,AMBN=.(2)解:图2中BNABBM=+;图3中BNBMAB=−.(3)证明:PAB和PMN是等边三角形,60ABPPMN==,ABPB=,120PBM
=,BMABPB==,30BMP=,90BMNPMNBMP=+=,MNAB⊥.【例8-5】如图,点O是等边ABC内一点,110AOB=,BOC=.以OC为一边作等边三角形OCD,连接AC、AD.(1)
当150=时,试判断AOD的形状,并说明理由;(2)探究:当为多少度时,AOD是等腰三角形?【解答】解:(1)OCD是等边三角形,OCCD=,而ABC是等边三角形,BCAC=,60ACBOCD==,BCOACD=,在BO
C与ADC中,OCCDBCOACDBCAC===,BOCADC,BOCADC=,而150BOC==,60ODC=,1506090ADO=−=,ADO是直角三角形;(2)设CBOCADa==,
ABOb=,BAOc=,CAOd=,则60ab+=,18011070bc+=−=,60cd+=,10bd−=,(60)10ad−−=,50ad+=,即50DAO=,①要使AOAD=,需AODADO=,19060−=−,125=;②要使O
AOD=,需OADADO=,1108060360+++=110=;③要使ODAD=,需OADAOD=,1105060360+++=,140=.所以当为110、125、140时,三角形AOD是等腰三角形.【模型拓展】【拓展8-1】已
知,在AOB和COD中,AOCO=,AOBCOD==,BD=,且A,O,D三点在同一条直线上.(1)如图1,求证:OBOD=;(2)如图2,连接AC、DB并延长交于点Q.当120=时,判断QAD的形状,并说明理由;(3)
如图3,过D点作DGAQ⊥,垂足为G,若4QB=,5DG=,当135=时,求QC的长.【解答】(1)证明:AOOC=,AOBCOD=,BD=,()AOBCODAAS,OBOD=;(2)解:QAD是等边三角形.理由如下:120AOBCOD==,60B
ODAOC==,OAOC=,OBOD=,60OACODB==,QAD是等边三角形;(3)在QA上取点H,使QHQB=,连接DH,QDQA=,QQ=,QHQB=,()QHDQBASAS,HDBA=,由(1)可知AOBCOD,ABCD=,
HDCD=,由(2)可知,当135=时,67.5OACODB==,45Q=,DGAQ⊥,5QGDG==,HDCD=,CGGH=,4QB=,4HQ=,1HGCG==,4116QCCGGHQH=++=++=.【拓展8-2】如图1,点A和点B分别在y轴正半轴和x轴负半轴上,
且OA=OB,点C和点D分别在第四象限和第一象限,且OC⊥OD,OC=OD,点D的坐标为(m,n),且满足(m﹣2n)2+|n﹣2|=0.(1)求点D的坐标;(2)求∠AKO的度数;(3)如图2,点P,Q分别在y轴正半轴和x轴负半轴上,
且OP=OQ,直线ON⊥BP交AB于点N,MN⊥AQ交BP的延长线于点M,判断ON,MN,BM的数量关系并证明.【解答】解:(1)∵(m﹣2n)2+|n﹣2|=0,又∵(m﹣2n)2≥0,|n﹣2|≥0,∴n
=2,m=4,∴点D坐标为(4,2).(2)如图1中,作OE⊥BD于E,OF⊥AC于F.∵OA=OB,OD=OC,∠AOB=∠COD=90°,∴∠BOD=∠AOC,∴△BOD≌△AOC,∴EO=OF(全等三角形对应边上的高相等),∴OK平分∠BKC,∴∠OBD=∠
OAC,易证∠AKB=∠BOA=90°,∴∠OKE=45°,∴∠AKO=135°.(3)结论:BM=MN+ON.理由:如图2中,过点B作BH∥y轴交MN的延长线于H.∵OQ=OP,OA=OB,∠AOQ=∠BOP=90°,∴△AOQ≌△BOP,∴
∠OBP=∠OAQ,∵∠OBA=∠OAB=45°,∴∠ABP=∠BAQ,∵NM⊥AQ,BM⊥ON,∴∠ANM+∠BAQ=90°,∠BNO+∠ABP=90°,∴∠ANM=∠BNO=∠HNB,∵∠HBN=∠OBN=45°,BN=BN,∴△
BNH≌△BNO,∴HN=NO,∠H=∠BON,∵∠HBM+∠MBO=90°,∠BON+∠MBO=90°,∴∠HBM=∠BON=∠H,∴MH=MB,∴BM=MN+NH=MN+ON.【拓展8-3】以△ABC的AB、AC为边作△ABD和△ACE,且AE=A
B,AC=AD,CE与BD相交于M,∠EAB=∠CAD=α.(1)如图1,若α=40°,求∠EMB的度数;(2)如图2,若G、H分别是EC、BD的中点,求∠AHG的度数(用含α式子表示);(3)如图3,连接AM,直接写出∠AMC与α的数量关系是.【解答
】解:(1)∵∠EAB=∠CAD=α,∴∠EAC=∠BAD,在△AEC和△ABD中,,∴△AEC≌△ABD(SAS),∴∠AEC=∠ABD,∵∠AEC+∠EAB=∠ABD+∠EMB,∴∠EMB=∠EAB=40°;(2)连接AG,
AH,由(1)可得:EC=BD,∠ACE=∠ADB,∵G、H分别是EC、BD的中点,∴DH=CG,在△ACG和△ADH中,,∴△ACG≌△ADH(SAS),∴AG=AH,∠CAG=∠DAH,∴∠AGH=∠AHG,∠CAG﹣∠CAH=∠DAH﹣∠CAH,∴∠G
AH=∠DAC,∵∠DAC=α,∴∠GAH=α,∵∠GAH+∠AHG+∠AGH=180°,∴∠AHG=90°﹣α;(3)如图3,连接AM,过点A作AP⊥EC于P,AN⊥BD于N,∵△ACE≌△ADB,∴S△ACE=S△ADB
,EC=BD,∵EC×AP=×BD×AN,∴AP=AN,又∵AP⊥EC,AN⊥BD,∴∠AME=∠AMD=,∴∠AMC=∠AMD+∠DMC=90°+α,故答案为:90°+α.【拓展8-4】如图,在ABC和
CDE中,90ACBDCE==,ACBC=,DCEC=.过点C作CFDE⊥交DE于点F.(1)如图1,当点B、E、D在同一条线上时,①求证:12CFDE=;②求BDA的度数;(2)如图2,连接AF并延长至
点G,使AFGF=,连接GE、GB,试判断BEG形状,并说明理由.【解答】(1)①证明:90DCE=,CDCE=,45CDFCEF==,CFDE⊥,90CFDCFE==,45CDFFCD==,45CEFFCE==,CFFD=,CFE
F=,12CFDE=;②如图1中,90DCEACB==,DCAECB=,在DCA和ECB中,DCECDCAECBCACB===,()DCAECBSAS,ADCBEC=,45CED=,18045135B
EC=−=,135ADCBEC==,45CDE=,1354590ADBADCCDE=−=−=;(2)结论:BEG是等腰直角三角形.理由:如图2中,延长BE交AD的延长线
于点T,交AC于点O.在AFD和GFE中,FAFGAFDGFEFDFE===,()AFDGFESAS,ADEG=,DAFEGF=,//ATEG,ADCECB,ADBE
=,DACCBE=,EGBE=,AOTBOC=,90TBCO==,//ATEG,90GETT==,90BEG=,BEG是等腰直角三角形.【拓展8-5】如图1,已知等腰ABC,ABAC=,120BAC
=,ADBC⊥于点D,点E是线段AD上一点,点F是CA延长线上一点,且EBEF=.(1)当点D与点E重合时,即DBDF=,如图2,求BFC的度数;(2)求证:AFEABE=;(3)求证:ABAEAF=+.【解答】(1)解:如图1,ABAC=,120BA
C=,30ACBABC==,ADBC⊥于点D,BDCD=,DBDF=,CDDF=,30DFC=,60BDF=BDDF=,BDF是等边三角形,90BFC=;(2)证明:ABAC=,120BAC=,30ABCACB==
,ABAC=,ADBC⊥,AD垂直平分BC,连接EC,则EBEC=,EBCECB=,EBEC=,EFEC=,EFCECF=,30AFEEBC+=,30ABEEBC+=,AFEABE=;(3)证明:由(2)知:60BAE=,60BADCAD==,120
FAE=,60BAF=,60BEF=,EBEF=,BEF为等边三角形,在边AB上取一点P,使得APAF=,APF为等边三角形,BFPAFE=,120BPFEAF==,PFAF=,()BPFEAFAAS
,BPAE=,ABBPPAAEAF=+=+.