【文档说明】《2022-2023学年八年级数学上册全等三角形模型图析高分突破（人教版）》全等变化模型七 对角互补四边形模型（原卷版）.docx，共(6)页，2.903 MB，由envi的店铺上传

转载请保留链接：https://www.doc5u.com/view-d0f4d101f6c6b784351c3f408a84a077.html

以下为本文档部分文字说明：

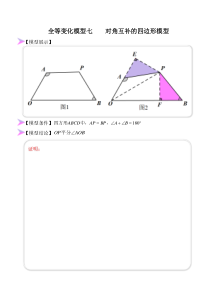
全等变化模型七对角互补的四边形模型【模型展示】【模型条件】=+=180BABPAPABCD，中，四方形【模型结论】AOBOP平分证明：【模型总结】AOBOPBABPAP=+=平分，③，②①180以三个条件，知二推一。【模型应用】如图3所

示，当点A在AO延长线上时：证明：【模型巩固】【例7-1】如图，四边形ABCD中，∠ABC+∠D＝180°，AC平分∠BAD，CE⊥AB，CF⊥AD．试说明：（1）△CBE≌△CDF；（2）AB+DF＝AF．【例7-2】如图1，在正方形ABCD中，

P是对角线BD上的点，点E在AB上，且PA＝PE．（1）求证：PC＝PE；（2）求∠CPE的度数；【例7-3】综合与探究如图，在ABC和ADE中，ABAC=，ADAE=，BACDAE=，CE的延

长线交BD于点F．（1）求证：ACEABD．（2）若50BACDAE==，请直接写出BFC的度数．（3）过点A作AHBD⊥于点H，求证：EFDHHF+=．【例7-4】如图，90BADCAE==，ABAD=，AEAC=，AFCB⊥，垂足为F

．（1）求证：ABCADE；（2）求FAE的度数；（3）求证：2CDBFDE=+．【例7-5】在ABC中，90C=，2ACBC==，将一块三角板的直角顶点放在斜边AB的中点P处，将此三角板绕点P旋转，三角板的两直角边分别交射线AC、CB于点D、点E，图①，②，③是旋转得到

的三种图形．（1）观察线段PD和PE之间有怎样的大小关系？并以图②为例，并加以证明；（2）观察线段CD、CE和BC之间有怎样的数量关系？并以图③为例，并加以证明；