【文档说明】《2022-2023学年八年级数学上册全等三角形模型图析高分突破（人教版）》全等变化模型二 一线三等角模型（解析版）.docx，共(8)页，3.018 MB，由envi的店铺上传

转载请保留链接：https://www.doc5u.com/view-9b0c80b7dcc58db10b2d436e265231bc.html

以下为本文档部分文字说明：

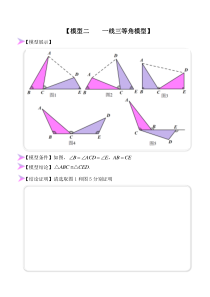
【模型二一线三等角模型】【模型展示】【模型条件】如图，CEABEACDB===，【模型结论】.CEDABC△△【结论证明】请选取图1和图5分别证明全等变化模型二一线三等角模型【模型解析】从变化方式的角度分析，两个全等三角形绕某一点旋转三角形的一个内角大小得到的，当一组非对应边共线时就会形

成等角。从图形的结构分析，一线三等角是一条直线上的三个等角加一组对应边相等组成的.【知识链接】三角形外角定理【模型总结】①一线三等角证明常用外角证明，一线三垂直用余角证明亦可。②一线三等角会形成等腰三角形，解题时要考虑。③三等角模

型，对应边夹角相等，都等于旋转角。【模型巩固】【例2-1】如图，在△ABC中，AB＝AC，点D在BC边上，点E在AC边上，连接AD、DE，若AD＝DE，AC＝CD．（1）求证：△ABD≌△DCE；（2）若B

D＝3，CD＝5，求AE的长．【证明】：∵AB＝AC，∴∠B＝∠C，∵AB＝AC，∴∠B＝∠C，∵AD＝DE，AC＝CD，∴∠AED＝∠DAE＝∠ADC，∴∠C+∠2＝∠B+∠1，∴∠1＝∠2，在△ABD与△DCE中，，∴△AB

D≌△DCE（AAS）；（2）解：∵△ABD≌△DCE，∴AB＝DC＝5，CE＝BD＝3，∵AC＝AB，∴AC＝5，∴AE＝AB﹣EC＝5﹣3＝2．【例2-2】如图，CD是经过BCA顶点C的一条直线，CACB=，E、F

分别是直线CD上两点，且BECCFA==．（1）若直线CD经过BCA的内部，且E、F在射线CD上．①如图1，若90BCA=，90=，则BE_____CF；②如图2，若0180BCA，请添加一个关于与BCA关系的条件，使①中的结论仍然成立，并说

明理由；（2）如图3，若直线CD经过BCA的外部，BCA=，请提出关于EF，BE，AF三条线段数量关系的合理猜想，并简述理由．【解答】解：（1）①90BECCFA===，18090BCECBEBEC+=−=．又90BCABCEACF=+=，CBEACF

=．在BCE和CAF中，,,BECCFACBEACFBCAC===()BCECAFAAS．BECF=．②180BCA+=，理由如下：BECCFA==，180180B

EFBEC=−=−．又BEFEBCBCE=+，180EBCBCE+=−．又180BCA+=，180BCA=−．180BCABCEACF=+=−．EBCFCA=．在BCE和CAF中，,,CBEACFBE

CCFABCCA===()BCECAFAAS．BECF=．（2）EFBEAF=+，理由如下：BCA=，180180BCEACFBCA+=−=−．又BEC=，18018

0EBCBCEBEC+=−=−．EBCFCA=．在BEC和CFA中，,,EBCFCABECFCABCCA===()BECCFAAAS．BECF=，ECFA=．EFECCFFABE=+=+.【例2-3】如图，已

知△ABC中，AB＝AC＝9cm，BC＝6cm，点D为AB的中点．（1）如果点P在边BC上以1.5cm/s的速度由点B向点C运动，同时，点Q在边CA上由点C向点A运动．①若点Q的运动速度与点P的运动速度相等，经过1秒后，△BPD与△CQP是否全等，请说明理由；②若点Q的运动速度与点P的运动速度不

相等，经过t秒后，△BPD与△CQP全等，求此时点Q的运动速度与运动时间t．（2）若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿△ABC三边运动，则经过秒后，点P与点Q第一

次在△ABC的边上相遇？（在横线上直接写出答案，不必书写解题过程）【解答】解：（1）①全等，理由如下：∵t＝1秒，∴BP＝CQ＝1×1.5＝1.5（厘米），∵AB＝9cm，点D为AB的中点，∴BD＝4.5cm．又∵PC＝BC﹣BP，BC＝6cm，∴PC＝6﹣1.5＝4.5（c

m），∴PC＝BD．又∵AB＝AC，∴∠B＝∠C，在△BDP和△CPQ中，，∴△BPD≌△CQP（SAS）；②假设△BPD与△CQP，∵vP≠vQ，∴BP≠CQ，又由∠B＝∠C，则只能是BP＝CP＝3，BD＝CQ＝4.5，∴点P，点Q运动的时间t＝BP÷1.

5＝3÷1.5＝2（秒），∴vQ＝CQ÷t＝4.5÷2＝2.25（cm/s）；（2）设经过x秒后点P与点Q第一次相遇，由题意，得2.25x＝1.5x+2×9，解得x＝24，∴点P共运动了24×1.5＝36（cm）．∴点P、点Q在AC边上相遇，∴经

过24秒点P与点Q第一次在边AC上相遇【例2-4】已知，在△ABC中，AB＝AC，D，A，E三点都在直线m上，且DE＝9cm，∠BDA＝∠AEC＝∠BAC（1）如图①，若AB⊥AC，则BD与AE的数量关系为，CE与AD

的数量关系为；（2）如图②，判断并说明线段BD，CE与DE的数量关系；（3）如图③，若只保持∠BDA＝∠AEC，BD＝EF＝7cm，点A在线段DE上以2cm/s的速度由点D向点E运动，同时，点C在线段EF上以xcm/s的速度由点E向点F运动，它们运动的时间

为t（s）．是否存在x，使得△ABD与△EAC全等？若存在，求出相应的t的值；若不存在，请说明理由．【解答】解：（1）∵∠BDA＝∠AEC＝∠BAC，∴∠BAD+∠CAE＝∠BAD+∠ABD，∴∠CAE＝∠ABD，∵∠BDA＝∠AEC，BA＝CA，∴△ABD≌△CAE（AAS），∴BD＝AE，C

E＝AD，故答案为：BD＝AE，CE＝AD；（2）DE＝BD+CE，由（1）同理可得△ABD≌△CAE（AAS），∴BD＝AE，CE＝AD，∴DE＝BD+CE；（3）存在，当△DAB≌△ECA时，∴AD＝CE＝2cm，BD＝AE＝7cm，∴t＝1，此时x＝2；当△DAB≌△EAC时，∴AD＝

AE＝4.5cm，DB＝EC＝7cm，∴t＝，x＝7÷＝，综上：t＝1，x＝2或t＝，x＝．【例2-5】已知，M是等边△ABC边BC上的点．（1）如图1，过点M作MN∥AC且交于点N，求证：BM＝BN；（2）如图

2，连接AM，过点M作∠AMH＝60°，MH与∠ACB的邻补角的平分线交于点H，过H作HD⊥BC于点D．求证：MA＝MH．【解答】解：（1）∵△ABC是等边三角形，∴∠A＝∠B＝∠C＝60°，AB＝BC＝AC．∵MN∥AC，∴∠BMN＝∠C＝60°，∠BNM＝∠A＝60°

．∴∠BMN＝∠BNM＝∠B＝60°，∴△BNM是等边三角形，∴BM＝BN；（2）过点M作MN∥AC交AB于N，∴BM＝BN，∠ANM＝120°．∵∠AMH＝60°，∴∠AMB+∠HMC＝120°．∵∠B＝60°，∴∠AMB+∠BAM＝120°．∴∠H

MC＝∠BAM．∵∠ACB＝60°，∴∠ACD＝120°．∵CH平分∠ACD，∴∠ACH＝∠ACD＝60°，∴∠MCH＝120°，∴∠ANM＝∠MCH．∵AB＝BC，∴AB﹣BN＝BC﹣BM，∴AN＝BC．在△ANM和△MCH中，，∴△AN

M≌△MCH（ASA），∴MA＝MH．