【文档说明】《2022-2023学年八年级数学上册全等三角形模型图析高分突破（人教版）》全等变化模型六 半角模型（原卷版）.docx，共(9)页，3.949 MB，由envi的店铺上传

转载请保留链接：https://www.doc5u.com/view-6825eba3a5aaa88319f5dd70a9c1214f.html

以下为本文档部分文字说明：

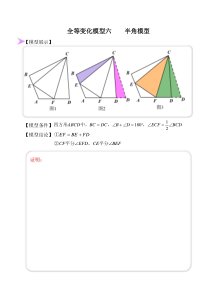
全等变化模型六半角模型【模型展示】【模型条件】BCDECFDBDCBCABCD==+=21180，，中，四方形【模型结论】FDBEEF+=①BEFCEEFDCF平分，平分②证明：【模型应用】【模型巩固】【例6-1】如图，正方形ABCD

中，∠EAF的两边分别与边BC、CD交于点E、F，AE、AF分别交BD于点G、H，且∠EAF＝45°．（1）当∠AEB＝55°时，求∠DAH的度数；（2）设∠AEB＝α，则∠AFD＝（用含α的代数式表示）；（3）求证：∠AEB＝∠AEF．【例6-2】在正方形AB

CD中，已知∠MAN＝45°，AH⊥MN，垂足为H，若M、N分别在边CB、DC的延长线上移动．①试探究线段MN、BM、DN之间的数量关系．②求证：AB＝AH．【例6-3】如图（1），在平面直角坐标系中，AB⊥x轴

于B，AC⊥y轴于C，点C（0，4），A（4，4），过C点作∠ECF分别交线段AB、OB于E、F两点（1）若OF+BE＝AB，求证：CF＝CE．（2）如图（2），且∠ECF＝45°，S△ECF＝6，求S△BEF的值．【例6-4】如图，在正方形ABCD中，M、N分别是射线C

B和射线DC上的动点，且始终∠MAN＝45°．（1）如图1，当点M、N分别在线段BC、DC上时，请直接写出线段BM、MN、DN之间的数量关系；（2）如图2，当点M、N分别在CB、DC的延长线上时，（1）中的结论是否仍然成立，若成

立，给予证明，若不成立，写出正确的结论，并证明；【模型拓展】【拓展6-1】如图，已知(,)Aab，ABy⊥轴于B，且满足22(2)0ab−+−=，（1）求A点坐标；（2）分别以AB，AO为边作等边三角形ABC和AOD，如图1试判定线段AC和DC的数量关系和位置关系．（3）如图2过A作A

Ex⊥轴于E，F，G分别为线段OE，AE上的两个动点，满足45FBG=，试探究OFAGFG+的值是否发生变化？如果不变，请说明理由并求其值；如果变化，请说明理由．【拓展6-2】如图1，点A、D在y轴正半轴上，点B、C分别在x

轴上，CD平分ACB与y轴交于D点，90CAOBDO=−．（1）求证：ACBC=；（2）在（1）中点C的坐标为(4,0)，点E为AC上一点，且DEADBO=，如图2，求BCEC+的长；（3）在（1）中，过D作DFAC⊥于F点，点H为FC上一动点，点G为OC上一动点，（如图3)，当点H

在FC上移动、点G在OC上移动时，始终满足GDHGDOFDH=+，试判断FH、GH、OG这三者之间的数量关系，写出你的结论并加以证明．【拓展6-3】如图1，ACB为等腰三角形，90ABC=，点P在线段BC上（不与B，C重合），以AP为腰长作等腰直角PAQ

，QEAB⊥于E．（1）求证：PABAQE；（2）连接CQ交AB于M，若2PCPB=，求PCMB的值；（3）如图2，过Q作QFAQ⊥交AB的延长线于点F，过P点作DPAP⊥交AC于D，连接DF，当点P在线段BC上运动时（不与B，C重合），式子QFDP

DF−的值会变化吗？若不变，求出该值；若变化，请说明理由．