【文档说明】《2022-2023学年八年级数学上册全等三角形模型图析高分突破（人教版）》全等变化模型八 手拉手模型（原卷版）.docx，共(11)页，3.965 MB，由envi的店铺上传

转载请保留链接：https://www.doc5u.com/view-7c65dfeef880880c0c09211507cef042.html

以下为本文档部分文字说明：

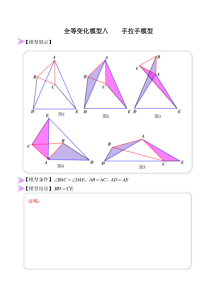
全等变化模型八手拉手模型【模型展示】【模型条件】AEADACABDAEBAC===，，【模型结论】CEBD=证明：【模型应用】如下图所示：三点共线、、，且和等边等边△,DCACDEABC请对以上结论（5）、结论（6）结论（7）进行证明。证明：ODOCOEOCOBOAAOECOBQA

PAEPQPCQAOBACBBEAD+=+====⑧、⑦、平分⑥、⑤、∥④、为等边三角形③、△②、①、【模型巩固】【例8-1】如图，在等腰△ABC中，BA＝BC，点F在AB边上，延长CF交AD于点E，BD＝BE，∠ABC＝∠D

BE．（1）求证：AD＝CE；（2）若∠ABC＝30°，∠AFC＝45°，求∠EAC的度数．【例8-2】如图，已知△ABC为等边三角形，D为BC延长线上的一点，CE平分∠ACD，CE＝BD，求证：（1）△ABD≌△ACE；（2）试判断△ADE的形状，并证明．【例8-3】如图，C

A＝CB，CD＝CE，∠ACB＝∠DCE＝α，AD、BE交于点H，连CH．（1）求证：△ACD≌△BCE；（2）求证：CH平分∠AHE；（3）求∠CHE的度数．（用含α的式子表示）【例8-4】如图1，点M为直线AB上一动点，PAB，PMN都是等边三角形，连接

BN（1）求证：AMBN=；（2）分别写出点M在如图2和图3所示位置时，线段AB、BM、BN三者之间的数量关系（不需证明）；（3）如图4，当BMAB=时，证明：MNAB⊥．【例8-5】如图，点O是等边ABC内一点，110AOB

=，BOC=．以OC为一边作等边三角形OCD，连接AC、AD．（1）当150=时，试判断AOD的形状，并说明理由；（2）探究：当为多少度时，AOD是等腰三角形？【模型拓展】【拓展8-1】已知，在AOB和COD中，AOCO=，AOBC

OD==，BD=，且A，O，D三点在同一条直线上．（1）如图1，求证：OBOD=；（2）如图2，连接AC、DB并延长交于点Q．当120=时，判断QAD的形状，并说明理由；（3）如图3，过D点作DGAQ⊥，垂足为G，若4QB=，5DG=，当135=时，求QC的长．【拓

展8-2】如图1，点A和点B分别在y轴正半轴和x轴负半轴上，且OA＝OB，点C和点D分别在第四象限和第一象限，且OC⊥OD，OC＝OD，点D的坐标为（m，n），且满足（m﹣2n）2+|n﹣2|＝0．（1）求点

D的坐标；（2）求∠AKO的度数；（3）如图2，点P，Q分别在y轴正半轴和x轴负半轴上，且OP＝OQ，直线ON⊥BP交AB于点N，MN⊥AQ交BP的延长线于点M，判断ON，MN，BM的数量关系并证明．【拓展8-3】以△ABC的AB、AC为边作△ABD和△ACE，且

AE＝AB，AC＝AD，CE与BD相交于M，∠EAB＝∠CAD＝α．（1）如图1，若α＝40°，求∠EMB的度数；（2）如图2，若G、H分别是EC、BD的中点，求∠AHG的度数（用含α式子表示）；（3）如图3，连接AM，直接写出∠AMC与α的数量关

系是．【拓展8-4】如图，在ABC和CDE中，90ACBDCE==，ACBC=，DCEC=．过点C作CFDE⊥交DE于点F．（1）如图1，当点B、E、D在同一条线上时，①求证：12CFDE=；②求BD

A的度数；（2）如图2，连接AF并延长至点G，使AFGF=，连接GE、GB，判断BEG形状，并说明理由．【拓展8-5】如图1，已知等腰ABC，ABAC=，120BAC=，ADBC⊥于点D，点E是线段AD上一点，点F是CA延长线上一点，且EBEF=．（1）当点D与点E重合时，即

DBDF=，如图2，求BFC的度数；（2）求证：AFEABE=；（3）求证：ABAEAF=+．