【文档说明】《2022-2023学年八年级数学上册全等三角形模型图析高分突破（人教版）》全等变化模型七 对角互补四边形模型（解析版）.docx，共(8)页，3.062 MB，由envi的店铺上传

转载请保留链接：https://www.doc5u.com/view-cf9e54798b6309555a77bab74d50e800.html

以下为本文档部分文字说明：

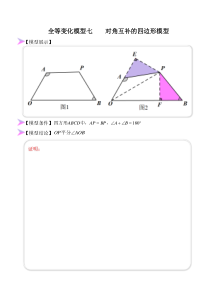
全等变化模型七对角互补的四边形模型【模型展示】【模型条件】=+=180BABPAPABCD，中，四方形【模型结论】AOBOP平分证明：【模型总结】AOBOPBABPAP=+=平分，③，②①18

0以三个条件，知二推一。【模型应用】如图3所示，当点A在AO延长线上时：证明：【模型巩固】【例7-1】如图，四边形ABCD中，∠ABC+∠D＝180°，AC平分∠BAD，CE⊥AB，CF⊥AD．试说明：（1）△CBE≌△CDF；（2）AB+DF＝AF．【解答】证

明：（1）∵AC平分∠BAD，CE⊥AB，CF⊥AD∴CE＝CF∵∠ABC+∠D＝180°，∠ABC+∠EBC＝180°∴∠EBC＝∠D在△CBE与△CDF中，∴△CBE≌△CDF；（2）在Rt△ACE与Rt△ACF中，∴△ACE≌△ACF∴AE＝AF∴AB+D

F＝AB+BE＝AE＝AF．【例7-2】如图1，在正方形ABCD中，P是对角线BD上的点，点E在AB上，且PA＝PE．（1）求证：PC＝PE；（2）求∠CPE的度数；【解答】（1）证明：在正方形ABCD中，AB＝BC，∠ABP＝∠CBP＝45°，在△ABP和△CBP中，，∴△

ABP≌△CBP（SAS），∴PA＝PC，∵PA＝PE，∴PC＝PE；（2）解：由（1）知，△ABP≌△CBP，∴∠BAP＝∠BCP，∵PA＝PE，∴∠PAE＝∠PEA，∴∠CPB＝∠AEP，∵∠AEP+∠PEB＝180°，∴∠PEB+∠PCB＝180°，∴∠ABC+∠EPC

＝180°，∵∠ABC＝90°，∴∠EPC＝90°；【例7-3】综合与探究如图，在ABC和ADE中，ABAC=，ADAE=，BACDAE=，CE的延长线交BD于点F．（1）求证：ACEABD．（2）若50BACDAE==，请

直接写出BFC的度数．（3）过点A作AHBD⊥于点H，求证：EFDHHF+=．【解答】（1）证明：BACDAE=．CAEBAD=．在ACE和ABD中，ACABCAEBADAEAD===，()ACEABDSAS；（2）解：ACEABD，AEC

ADB=，180AEFAECAEFADB+=+=．180DAEDFE+=，180BFCDFE+=，50BFCDAEBAC===；（3）证明：如图，连接AF，过点A作AJCF⊥于点J．ACEABD，ACEA

BDSS=，CEBD=，AJCE⊥，AHBD⊥．1122CEAJBDAH=，AJAH=．在RtAFJ和RtAFH中，AFAFAJAH==，RtAFJRtAFH(HL)，FJFH=．在RtAJE和RtAHD中，AEADAJAH==，R

tAJERtAHD(HL)，EJDH=，EFDHEFEJFJFH+=+==．【例7-4】如图，90BADCAE==，ABAD=，AEAC=，AFCB⊥，垂足为F．（1）求证：ABCADE；（2）求FAE的度数；（3）求证：

2CDBFDE=+．【解答】证明：（1）90BADCAE==，90BACCAD+=，90CADDAE+=，BACDAE=，在BAC和DAE中，ABADBACDAEACAE=

==，()BACDAESAS；（2）90CAE=，ACAE=，45E=，由（1）知BACDAE，45BCAE==，AFBC⊥，90CFA=，45CAF

=，4590135FAEFACCAE=+=+=；（3）延长BF到G，使得FGFB=，AFBG⊥，90AFGAFB==，在AFB和AFG中，BFGFAFBAFGAFAF===，()AFBAFGSAS

，ABAG=，ABFG=，BACDAE，ABAD=，CBAEDA=，CBED=，AGAD=，ABFCDA=，GCDA=，45GCADCA==，在CGA和CDA中，GCADCACGACDAAGAD===，()CGACDAA

AS，CGCD=，22CGCBBFFGCBBFDEBF=++=+=+，2CDBFDE=+．【例7-5】在ABC中，90C=，2ACBC==，将一块三角板的直角顶点放在斜边AB的中点P处，将此三角板绕点P旋转，三角板的

两直角边分别交射线AC、CB于点D、点E，图①，②，③是旋转得到的三种图形．（1）观察线段PD和PE之间有怎样的大小关系？并以图②为例，并加以证明；（2）观察线段CD、CE和BC之间有怎样的数量关系？并以图③为例，并加以证明；【

解答】解：（1）PDPE=，理由如下：如图②，连接PC，ABC是等腰直角三角形，P为斜边AB的中点，12PCABPB==，CPAB⊥，1452DCPACB==，DCPB=，又90DPCCPE

+=，90CPEEPB+=，DPCEPB=，在DPC和EPB中，DCPBPCPBDPCEPB===，()DPCEPBASA，PDPE=；（2）CDBCCE+=，理

由如下：连接CP，如图③所示：同（1）得：()DPCEPBASA，CDBE=，BEBCCE+=，CDBCCE+=；