【文档说明】《一隅三反系列之高二数学新教材选择性必修第二册（人教A版）》4.2.2 等差数列的前n项和（精讲）（原卷版）.docx，共(8)页，925.629 KB，由管理员店铺上传

转载请保留链接：https://www.doc5u.com/view-6db4d9267d638f9731e67b7a63b5e545.html

以下为本文档部分文字说明：

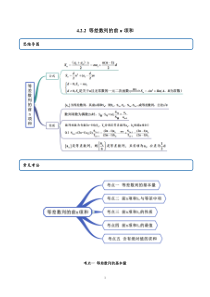
14.2.2等差数列的前n项和考点一等差数列的基本量思维导图常见考法2【例1】（2020·陕西省安康中学其他（理））记nS为等差数列na的前n项和，3242SSS+=，11a=，则7S=（）A．-77B．-

70C．-49D．-42【一隅三反】1．（2020·内蒙古赤峰）若等差数列na的前n项和为nS，且满足44a=，410S=，则公差d=（）A．1B．1−C．2D．2−2．（2020·河南信阳·其他（文））正项等差数列na的前n和为nS，已

知2375150aaa+−+=，则9S=（）A．35B．36C．45D．543．（2020·湖北十堰）已知等差数列na的前n项和nS满足3318,180,270nnSSS−===，则n=（）A．12B．13C．14D．15考点二前n项和Sn

与等差中项【例2】(1）（2020·云南省云天化中学高一期末）等差数列na中，3912aa+=，则数列na前11项和11S=（）A．12B．60C．66D．72（2）．（2020·吉林朝阳·长春外国语学校开学考试）设nS是等差数列na的前n

项和，若535,9aa=则95SS=（）A．1B．1−C．2D．12【一隅三反】（1）如果na为等差数列，若mnpq++＝，则mnpqaaaa++＝()*mnpqN，，，．(2)要注意等差数列前n项和公

式的灵活应用，如21(21)nnSna−=−.31．（2020·四川成都·二模（文））若数列na为等差数列，且满足5383aaa++＝，nS为数列na的前n项和，则11S＝（）A．27B．33C．3

9D．442．（2020·河北运河·沧州市一中月考）若两个等差数列nanb的前n项和分别为nS，nT，且满足3122nnSnTn−=+，则66ab=（）A．2B．74C．32D．433．（2020·河北新华·石家庄新世纪外国语学校期中）两等差数列na和nb，前n项和分别为nS，n

T，且723nnSnTn+=+，则220715aabb++的值为（）A．14924B．7914C．165D．51104．（2020·湖南宁乡一中）在等差数列na中，35710133()2()24aaaaa++++=，则此数列前13项的和是（）．

A．13B．26C．52D．56考点三前n项和Sn的性质【例3】（1）（2020·陕西省洛南中学高二月考）已知某等差数列共有10项，其奇数项之和为15，偶数项之和为30，则其公差为()A．6B．5C．4D．3（2）．（2019·陕西武功·高三月考（理））设等差数列na的前n项和为n

S若39S=,627S=，则9S=()A．45B．54C．72D．81（3）（2020·浙江吴兴·湖州中学）设nS为等差数列na的前n项和，且12010a=−，20112008320112008SS−=，则2011S=（）4A．0B．2011C．2009D．2010【一隅三反】1．

（2020·山东省临沂第一中学高二期中）一个等差数列共有3n项，若前2n项的和为100，后2n项的和为200，则中间n项的和为（）A．75B．100C．50D．1252．（2020·河北运河·沧州市一中月考）nS是等差数列na}的前n项和，若3613SS=，则612SS

为（）A．310B．13C．18D．193．（2020·黑龙江龙凤·大庆四中月考（理））在等差数列na中，12018a=−，其前n项和为nS，若151051510SS−=，则2020S=（）A．0B．2018C．2019−D．2020考点四前n项和Sn的最值【例4】（2020·陕西省洛南中学高

二月考）已知数列{}na中1116,2(*)nnaaanN+=−=−，则数列{}na的前n项和nS最大时，n的值为（）A．8B．7或8C．8或9D．9【一隅三反】一般地，如果na为等差数列，nS为其前

n项和，则有性质：（1）若,,,*,mnpqNmnpq+=+，则mnpqaaaa+=+；（2）()1,1,2,,2knknnaaSkn+−+==且()2121nnSna−=−；（3）2nSAnBn=+且nSn为等差数列；（4）232,,,nnnnnSSSSS−−为等差数列51．（2

021·河南淇滨·鹤壁高中高二月考）等差数列{an}的前n项和为Sn，S100＞0，S101＜0，则满足anan+1＜0的n＝（）A．50B．51C．100D．1012．（2020·吉林南关·长春市实验中学）已知数列na是等差数列，若91130aa+，

10110aa，且数列na的前n项和nS有最大值，那么nS取得最小正值时n等于（）A．1B．20C．10D．193．（2020·安徽金安·六安一中）已知等差数列na的前n项和为nS，130S，140S，则当S取得最小值时，n的值为（）A

．4B．6C．7D．84．（2020·安徽金安·六安一中）已知等差数列na的前n项和为nS，若190S，200S，则11Sa，22Sa，…，2020Sa中最大的是（）A．88SaB．99SaC．1100SaD．1111

Sa考点五含有绝对值的求和【例5】（2021·河南淇滨·鹤壁高中高二月考）已知两个等差数列na、nb，其中11a=，16b=，30b=，记na前n项和为nT，222nnnT=+．（1）求数列na与nb的通项公式；6（2）记nnncab=+，

设123nnScccc=++++，求nS．【一隅三反】1．（2019·浙江吴兴·湖州中学）已知等差数列{}na中，257a=−，1712a=−，记nnba=，记{}na的前n项和为nS，{}nb的前n项和为nT.（1）求首项1a和公差d；（2）求nS和nT的表达式2．（2020·安徽

月考）已知数列na的前n项和为nS，且219nSnn=−(*nN).（1）求nS的最小值；（2）求数列na的前20项和.73．（2020·商丘市第一高级中学期末）已知数列na的前n项和27nSnn=−．（1）求na的通项公式

；（2）求数列na的前n项和nT．8获得更多资源请扫码加入享学资源网微信公众号www.xiangxue100.com