【文档说明】新教材2022版数学苏教版必修第一册提升训练：第7章 三角函数 专题强化练11 三角函数图象与性质的应用含解析.docx，共(8)页，86.702 KB，由小赞的店铺上传

转载请保留链接：https://www.doc5u.com/view-b92ce254a217a3364d615a7b83016c6e.html

以下为本文档部分文字说明：

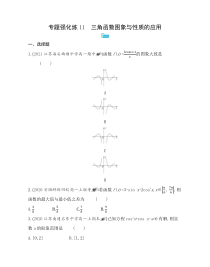
专题强化练11三角函数图象与性质的应用一、选择题1.(2021江苏海安曲塘中学高一期中,)函数f(x)=3cos𝑥+1𝑥的图象大致是()ABCD2.(2020安徽蚌埠四校高一上联考,)若函数f(x)

=3-sinx-2cos2x,x∈[π6,7π6],则函数的最大值与最小值之差为()A.38B.58C.78D.983.(2020江苏南通启东中学高一上期末,)已知方程cos2x+cosx-a=0有解,

则实数a的取值范围是()A.[0,2]B.[1,2]C.[-14,2]D.[-14,+∞)4.(2020辽宁营口二中高一下期末,)函数y=log12cos(3π2-2𝑥)的单调递增区间是(易错)A.

[𝑘π-π4,𝑘π+π4](k∈Z)B.[𝑘π-π4,𝑘π)(k∈Z)C.[𝑘π+π4,𝑘π+3π4](k∈Z)D.[𝑘π+π4,𝑘π+3π4)(k∈Z)5.(多选)(2021湖南名校联考联合体高一上大联考,)

给出下面四个结论,其中正确的是()A.函数f(x)=tan(π+π2𝑥)是奇函数,且f(x)的最小正周期为2B.函数f(x)=-2sin(2x+φ),x∈R的最大值为2,当且仅当φ=π2+kπ,k∈Z时,f(x)为偶函数C.函数f(x)=tan(-x)的单调递增区间是

(-π2+𝑘π,π2+𝑘π),k∈ZD.函数f(x)=sin(-12𝑥+π3),x∈[-2π,2π]的单调递减区间是[-π3,5π3]6.(2020河南信阳高一下期末,)已知函数f(x)=2sin(𝜔𝑥+π3)(ω>0

),若使得f(x)在区间[-π3,𝜑]上为增函数的整数ω有且仅有一个,则实数φ的取值范围是()A.[π6,π3]B.(π6,π3]C.[π12,π6]D.(π12,π6]二、填空题7.(2020江苏徐州丰县民族中学高一检测,)函数f(x)=lgcosx+√25-𝑥2的定义域为.8.(

)方程sinx=1-𝑎2在𝑥∈[π3,π]上有两个实数解,则实数a的取值范围是.三、解答题9.()若函数y=sin2x+acosx-12𝑎−32的最大值为1,求a的值.10.(2020天津一中高一上期末,)已知函数f(x)=m-22𝑥+1是定义在R上的奇函数.(1)求实数m的值

;(2)如果对任意x∈R,不等式f(2a+cos2x)+f(4sinx-√2𝑎-1-7)<0恒成立,求实数a的取值范围.答案全解全析专题强化练11三角函数图象与性质的应用一、选择题1.A易得f(x)的定义域为{x|x≠0},关于原点对称.又f(-x

)=3cos(-𝑥)+1-𝑥=−3cos𝑥+1𝑥=-f(x),故f(x)为奇函数,排除C,D;当x∈(0,π2)时,f(x)>0,故排除B.故选A.2.D设sinx=t,∵x∈[π6,7π6],∴t∈[-12,1].由f(

x)=3-sinx-2cos2x=2sin2x-sinx+1,得y=2t2-t+1=2(𝑡-14)2+78,t∈[-12,1].易知当t=-12或1时,y=2t2-t+1取得最大值2;当t=14时,y=2t2-t+1取得最小值78.∴函数f(x)的最大值与最小值之差

为98.故选D.3.C设f(x)=cos2x+cosx,g(x)=a,则方程cos2x+cosx-a=0有解⇔函数f(x)=cos2x+cosx的图象与函数g(x)=a的图象有交点.易得f(x)=co

s2x+cosx=(cos𝑥+12)2−14∈[-14,2],所以a∈[-14,2].故选C.4.B原函数可化为y=log12(-sin2x).由-sin2x>0得sin2x<0,即2kπ-π<2x<2kπ,k∈Z,即kπ-π2<x<kπ,k∈Z

.设t=-sin2x,kπ-π2<x<kπ,k∈Z.求y=log12cos(3π2-2𝑥)的单调递增区间,即求t=-sin2x,kπ-π2<x<kπ,k∈Z的单调递减区间,即求y=sin2x,kπ-π2<x<kπ,k∈Z的单调递增区间.令2kπ-π2≤2𝑥≤2𝑘π+π2

,k∈Z,得kπ-π4≤𝑥≤𝑘π+π4,k∈Z,又kπ-π2<x<kπ,k∈Z,所以y=log12cos(3π2-2𝑥)的单调递增区间是[𝑘π-π4,𝑘π)(k∈Z).故选B.易错警示解决与三角函数有

关的复合函数的单调性问题,应先求函数的定义域,再求单调区间,解题时防止漏求函数的定义域导致解题错误.5.ABD易得函数f(x)=tan(π+π2𝑥)=tanπ2x是奇函数,最小正周期T=2ππ=2,所以A正确;函数f(x)=-2sin(2x+φ),x∈R的最大值为2,当φ=π2+kπ,k∈Z时

,f(x)=-2cos(2x+kπ)=±2cos2x,k∈Z,为偶函数,所以B正确;函数f(x)=tan(-x)=-tanx,没有单调递增区间,所以C不正确;函数f(x)=sin(-12𝑥+π3)=−sin12𝑥−π3,x

∈[-2π,2π],令-π2+2𝑘π≤12𝑥−π3≤π2+2kπ,k∈Z,得-π3+4𝑘π≤𝑥≤5π3+4kπ,k∈Z,当k=0时,函数的单调递减区间是[-π3,5π3],所以D正确.故选ABD.6.D

因为f(x)在区间[-π3,𝜑]上为增函数,所以{-π2+2𝑘π≤π3-𝜔π3,𝜔𝜑+π3≤π2+2𝑘π,k∈Z,可得{0<𝜔≤52-6𝑘,①𝜔𝜑≤π6+2𝑘π,②k∈Z.当-π3<φ≤0时,满足题

意的整数ω至少有1,2,舍去.当φ>0,k=0时,由①得ω∈(0,52],由②得0<ω≤π6𝜑=π6𝜑.要使整数ω有且仅有一个,需1≤π6𝜑<2,解得π12<𝜑≤π6,所以实数φ的取值范围为(π12,π6].故选D.二、填空题7.答案[-5,-3π2)∪(-

π2,π2)∪3π2,5解析由题意得,x满足不等式组{cos𝑥>0,25-𝑥2≥0,即{cos𝑥>0,-5≤𝑥≤5.作出y=cosx(-5≤x≤5)的图象,如图所示.结合图象可得定义域为[-5,-3π2)∪

(-π2,π2)∪(3π2,5].8.答案(-1,1-√3]解析在平面直角坐标系中作出y=sinx,x∈[π3,π]的大致图象,如图所示.由图可知,当√32≤1-𝑎2<1,即-1<a≤1-√3时,y=sinx,x∈[π3,π]的图象与𝑦=1-𝑎2的图象有两个交点

,即方程sinx=1-𝑎2在𝑥∈[π3,π]上有两个实数解.三、解答题9.解析y=sin2x+acosx-12𝑎−32=1−cos2𝑥+𝑎cos𝑥−12𝑎−32=−cos2𝑥+𝑎cos𝑥−12𝑎−12=−(cos𝑥-𝑎2)2+𝑎24−12𝑎−12.

设cosx=t.∵-1≤cosx≤1,∴-1≤t≤1,∴函数y=-(cos𝑥-𝑎2)2+𝑎24−12𝑎−12的最大值为1等价于二次函数𝑦=−(𝑡-𝑎2)2+𝑎24−12𝑎−12在[-1,1]上的最大值为1.①当𝑎2<-1,

即a<-2时,函数在t=-1时取得最大值,为-32𝑎−32,由题意可知-32𝑎−32=1,解得a=-53,不符合题意;②当-1≤𝑎2≤1,即-2≤a≤2时,函数在t=𝑎2时取得最大值,为𝑎24−𝑎2−12,由题意可知𝑎24−𝑎2−12=1,解得a=1-√7或𝑎=1

+√7(舍去);③当𝑎2>1,即a>2时,函数在t=1时取得最大值,为𝑎2−32,由题意可知𝑎2−32=1,解得a=5.综上,a=1-√7或a=5.10.解析(1)因为f(x)是定义在R上的奇函数,所以f(-x)=-f(

x),即m-22𝑥+1+𝑚−22-𝑥+1=0,即2m-2=0,故m=1.(2)由(1)得f(x)=1-22𝑥+1.任取x1,x2∈R,且x1<x2,则f(x1)-f(x2)=21+2𝑥2−21+2𝑥1=2(2𝑥1

-2𝑥2)(1+2𝑥1)(1+2𝑥2).因为x1<x2,所以2𝑥1<2𝑥2,所以f(x1)-f(x2)<0,所以f(x1)<f(x2),所以函数f(x)在R上是增函数.因为f(2a+cos2x)+f(4sinx-

√2𝑎-1-7)<0,且f(x)是奇函数,所以f(2a+cos2x)<-f(4sinx-√2𝑎-1-7)=f(√2𝑎-1-4sinx+7),所以2a+cos2x<√2𝑎-1-4sinx+7,所以2a-√2𝑎-1<-cos2x-4sin

x+7对任意x∈R都成立.由于y=-cos2x-4sinx+7=(sinx-2)2+2,其中-1≤sinx≤1,所以(sinx-2)2+2≥3,所以y=-cos2x-4sinx+7的最小值为3.所以2a-√2𝑎-1<3,即2a-1-√2𝑎-1-2<0,解得0≤√2𝑎-1<2,所以

12≤𝑎<52.故实数a的取值范围是{𝑎|12≤𝑎<52}.获得更多资源请扫码加入享学资源网微信公众号www.xiangxue100.com