【文档说明】《鲁教版（五四制）九年级数学专题复习训练》专题9圆—9.10几何证明.doc，共(19)页，2.119 MB，由管理员店铺上传

转载请保留链接：https://www.doc5u.com/view-960940a01c4ab18c8e664aeee438914d.html

以下为本文档部分文字说明：

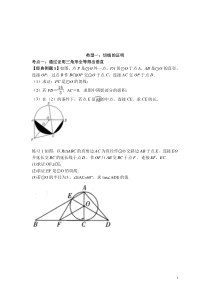
1类型一：切线的证明考点一：通过证明三角形全等得出垂直【经典例题1】如图，点P是⊙O外一点，PA切⊙O于点A，AB是⊙O的直径，连接OP，过点B作BC∥OP交⊙O于点C，连接AC交OP于点D．（1）求证：PC是⊙O的切线；（2）若PD＝，AC＝8，求图中阴

影部分的面积；（3）在（2）的条件下，若点E是的中点，连接CE，求CE的长．练习1如图，以RtABC的直角边AC为直径作⊙O交斜边AB于点E，连接EO并延长交BC的延长线于点D，作//OFAB交BC于点F，连接.EFEC、(1)求证:OF⊥CE；(2)求证:EF是

⊙O的切线;(3)若⊙O的半径为3，∠EAC=60°，求tan∠ADE的值.2考点二：通过平行（垂直，互余等）【经典例题2】如图，M，N是以AB为直径的⊙O上的点，且弧AN=弧BN，弦MN交AB于点C，BM平分

∠ABD，MF⊥BD于点F，（1）求证：MF是⊙O的切线；（2）若CN=3，BN=4，求CM的长.如图，圆O是ABC△的外接圆，AE平分BAC交圆O于点E，交BC于点D，过点E作直线lBC∥．（1）判断直线l与圆O的关系，并说明理由；（2）若ABC的平分线BF交AD于点F，求证：BEEF=；（

3）在（2）的条件下，若5DE=，3DF=，求AF的长．3如图，四边形ABCD中，AB=AD=CD，以AB为直径的⊙O经过点C，连接AC、OD交于点E.(1)证明：OD∥BC；(2)若tan∠ABC=2，证明：DA与⊙O相切；(3)

在(2)条件下，连接BD交⊙O于点F，连接EF，若BC=1，求EF的长。4考点三：与三角函数结合（定义、解三角形）【经典例题3】如图，AB为⊙O直径，AC为弦，过⊙O外的点D作DE⊥OA于点E，交AC于点F，连

接DC并延长交AB的延长线于点H，且∠D=2∠A.(1)求证：DC与⊙O相切；(2)若⊙O半径为4，cosD＝54，求AC的长.如图，已知AB是圆O的直径，弦CD⊥AB，垂足为H，与AC平行的圆O的一条切线交CD的延长线于点M，交AB的延长线于点E，切点为

F，连接AF交CD于点N．（1）求证：CA＝CN；（2）连接DF，若cos∠DFA＝，AN＝2，求圆O的直径的长度．如图，已知BD为⊙O的直径，AB为⊙O的一条弦，过⊙O外一点P作PO⊥AB，5垂足为点C，且交⊙O于点N，PO的延长线交

⊙O于点M，连接BM、AD、AP.(1)求证：PM∥AD；(2)若∠BAP=2∠M，求证：PA是⊙O的切线；(3)若AD=6，tan∠M=21，求⊙O的半径.已知：如图所示，MN是⊙O的直径，B是圆上一点，NP平分∠BNM交圆于P，

过P作PA⊥BN于A.(1)求证：PA是⊙O的切线；(2)若MN=20，BN=12，求MP的长；(3)若D是ON的中点，过D作CD⊥ON交AP于C，若CD=19，tan∠MNP=43，求圆的半径.考点四：与相似三

角形结合【经典例题4】如图，AB为⊙O上一点，C为的中点，AC与BD相交于点E．(1)求证：DC2＝CE•AC；(2)若AE＝2，CE＝1，求⊙O的半径；6(3)若AB＝10，43ACDtan=，求四边形ABCD的面积．如图，△ABC内接

于⊙O，CD平分∠ACB交⊙O于D，过点D作PQ∥AB分别交CA、CB延长线于P、Q，连接BD．(1)求证：PQ是⊙O的切线；PQ∥AB；(2)求证：BD2=AC•BQ；(3)连OB，若tan∠PCD=31，求BDOB的值；(4)若AC·BQ=9，且∠ACB=60°，求弦AB的

长；如图，AF为⊙O的直径，点B在AF的延长线上，BE切⊙O于点E，过点A作AC⊥BE，交BE的延长线交于点C，交⊙O交于点D，连接AE，EF，FD，DE．(1)求证：EF＝ED．(2)求证：DF・AF＝2AE•EF．(3)若AE

＝4，DE＝2，求sin∠DFA的值．7如图，⊙O是△ABC的外接圆，AB是直径，D是AC中点，直线OD与⊙O相交于E，F两点，P是⊙O外一点，P在直线OD上，连接PA，PC，AF，且满足∠PCA＝∠ABC．(1)求证

：PA是⊙O的切线；(2)证明：EF2＝4OP•OD．(3)若BC＝8，tan∠AFP＝2:3，求DE的长．如图,AB、AC分别是O的直径和弦,点D为劣弧AC上一点,弦DE⊥AB分别交O于E,交AB于H,交AC

于F.P是ED延长线上一点且PC=PF.(1)求证：PC是O的切线；(2)点D在劣弧AC什么位置时,才能使AD2=DE⋅DF，为什么?(3)在(2)的条件下，若OH=1，AH=2，求弦AC的长。如图，点P为正方形ABCD的对角线AC上的一点，连接BP并延长交CD于点E，交AD的延长线

于点F，圆O是△DEF的外接圆，连接DP．（1）求证：DP是圆O的切线．8（2）若21tan=PDC，正方形ABCD的边长为4，求圆O的半径和线段OP的长.如图，已知⊙O是△ABC的外接圆，且BC为⊙O的直径，在

劣弧AC上取一点D，使弧CD=弧AB，将△ADC沿AD对折，得到△ADE，连接CE．（1）求证：CE是⊙O的切线；（2）若CE=3CD，劣弧CD的弧长为π，求⊙O的半径．23如图，AB是⊙O的直径，BE是弦，点D是弦BE上一点，连接OD并延长交⊙O于点C，连接BC

，过点D作FD⊥OC交⊙O的切线EF于点F．(1)求证：∠CBE=21∠F；(2)若⊙O的半径是32，点D是OC中点，∠CBE=15°，求线段EF的长．9如图1,已知AB是⊙O的直径,AM和BN是⊙O的两条切线,∠是⊙O的

半圆弧上一动点(不与A,B重合)，过点E的直线分别交射线AM、BN于D.C两点，且CB=CE.(1)求证：CD为⊙O的切线；(2)求证：AB2=4AD⋅BC；(3)如图2，连接OE并延长交AM于点F，连接CF.若∠ADE=2∠OFC，AD=1，求图中阴影部分的

面积。【解析】(1)证明：如图1，连接OE，OC，在△BCO与△ECO中,===BCCEOCOCOBOE，∴△BCO≌△ECO(SSS)，∴∠OEC=∠OBC，∵BN是⊙O的切线，∴AB是⊙O的直径，∴AB⊥BN，∴∠ABC=90∘，∴∠OEC=90∘，∴CD为⊙O的切线；(2)证明

：连接OC、OD，如图1所示：∵AM和BN是它的两条切线，∴AM⊥AB，BN⊥AB，∴AM∥BN，10∴∠ADE+∠BCE=180∘∵DC切⊙O于E，∴∠ODE=21∠ADE,∠OCE=21∠BCE，∴∠ODE+∠O

CE=90∘，∴∠DOC=90∘，∴∠AOD+∠COB=90∘，∵∠AOD+∠ADO=90∘，∴∠AOD=∠OCB，∵∠OAD=∠OBC=90∘，∴△AOD∽△BCO，∴AD/BO=OA/BC，∴OA2=AD⋅BC，∴(21AB)2=AD⋅BC,∴AB2=4AD⋅BC；(2)连接O

D，OC，如图2所示：∵∠ADE=2∠OFC，∴∠ADO=∠OFC，∵∠ADO=∠BOC，∠BOC=∠FOC，∴∠OFC=∠FOC，∴CF=OC，∴CD垂直平分OF，∴OD=DF，在△COD和△CFD中,===CDCDDFODCFOC，∴△COD≌△CFD(SSS)，

∴∠CDO=∠CDF，∵∠ODA+∠CDO+∠CDF=180∘，∴∠ODA=60∘=∠BOC，11∴∠BOE=120∘，在Rt△DAO,AD=333OA，Rt△BOC中,BC=3OB，∴AD:BC=1:3，∵AD

=1，∴BC=3,OB=3，∴图中阴影部分的面积S△OBC−S扇形OBE=2×21×3×3−−=•33360)3(1202，如图,在Rt△ABC内接于⊙O,∠ACB=90∘，BC=2，将斜边AB绕点A顺时针旋转一定的角度得到AD，过点D

作DE⊥AC于点E，∠DAE=∠ABC，DE=1，连接DO交⊙O于点F.(1)求证：AD是⊙O的切线；(2)连接FC交AB于点G,连接FB.求证：FG2=GO⋅GB.【解析】证明：(1)∵⊙O为Rt△ABC的外接圆∴O为斜边AB中点，AB为直

径∵∠ACB=90∘∴∠ABC+∠BAC=90∘∵∠DAE=∠ABC∴∠DAE+∠BAC=90∘∴∠BAD=180∘−(∠DAE+∠BAC)=90∘∴AD⊥AB∴AD是⊙O的切线(2)延长DO交BC于点H

，连接OC∵DE⊥AC于点E∴∠DEA=90∘∵AB绕点A旋转得到AD∴AB=AD在△DEA与△ACB中∠DEA=∠ACB=90∘，∠DAE=∠ABC，DA=AB∴△DEA≌△ACB(AAS)∴AE=BC=2，AC=DE=112∴AD=AB=522=+BC

AC∵O为AB中点∴AO=21AB=25∴AODE=25=ADAE∵∠DAO=∠AED=90∘∴△DAO∽△AED∴∠ADO=∠EAD∴DO∥EA∴∠OHB=∠ACB=90∘，即DH⊥BC∵OB=OC∴OH平分∠BOC,即∠BOH=21∠BO

C∵∠FOG=∠BOH,∠BFG=21∠BOC∴∠FOG=∠BFG∵∠FGO=∠BGF∴△FGO∽△BGF∴FG/BG=GO/GF∴FG2=GO⋅GB如图，点O是线段AH上一点，AH=3，以点O为圆心，OA的长为半径作⊙O，过点H作AH的垂线交⊙O于C，N两点，点B在线段CN的延长

线上，连接AB交⊙O于点M，以AB，BC为边作▱ABCD.(1)求证：AD是⊙O的切线；(2)若OH=31AH，求四边形AHCD与⊙O重叠部分的面积；13(3)若NH=31AH,BN=45，连接MN，求O

H和MN的长。【解析】（1）证明：∵四边形ABCD是平行四边形，∴AD∥BC，∵∠AHC=90°，∴∠HAD=90°，即OA⊥AD，又∵OA为半径，∴AD是⊙O的切线；（3）设⊙O半径OA=r=OC，OH=3-r，在Rt△OHC中，OH2+HC

2=OC2，∴（3-r）2+12=r2，∴r=35，则OH=34，在Rt△ABH中，AH=3，BH=45+1=49，则AB=415，在Rt△ACH中，AH=3，CH=NH=1，得AC=10，在△BMN和△BCA中，∠B=∠B，∠BMN=∠BC

A，∴△BMN∽△BCA，∴ABBNACMN=即314154510==MN，∴MN=310，OH=34，MN=310．如图，PA是⊙O的切线，切点为A，AC是⊙O的直径，连接OP交⊙O于E.过A点作AB⊥PO于点D，交⊙O于B，连接B

C，PB.(1)求证：PB是⊙O的切线；(2)求证：E为△PAB的内心；14(3)若cos∠PAB=1010，BC=1，求PO的长。【解析】(1)证明：连结OB，∵AC为⊙O的直径，∴∠ABC=90∘，∵AB⊥PO，∴PO∥BC∴∠AOP=∠C，∠POB=∠OBC

，OB=OC，∴∠OBC=∠C,∴∠AOP=∠POB，在△AOP和△BOP中，OA=OB，∠AOP=∠POB，PO=PO，∴△AOP≌△BOP(SAS)，∴∠OBP=∠OAP，∵PA为⊙O的切线，∴∠

OAP=90∘，∴∠OBP=90∘，∴PB是⊙O的切线；(2)证明：连结AE，∵PA为⊙O的切线，∴∠PAE+∠OAE=90∘，∵AD⊥ED，∴∠EAD+∠AED=90∘，∵OE=OA，∴∠OAE=∠AED，∴∠PAE=∠DAE，即EA平分∠PAD，∵PA、PD为⊙O的切线，∴PD平分∠A

PB∴E为△PAB的内心；(3)∵∠PAB+∠BAC=90∘,∠C+∠BAC=90∘，∴∠PAB=∠C，∴cos∠C=cos∠PAB=1010，在Rt△ABC中,cos∠C=BC/AC=1/AC=1010，15∴A

C=10,AO=210，∵△PAO∽△ABC，∴PO/AC=AO/BC，∴PO=BCAO⋅AC=1210×10=5.22.（本题8分）已知：如图，⊙O的直径AB垂直于弦CD，过点C的切线与直径AB的延长线相交于点P，连结PD．⑴.求证：PD是⊙O的切线

．⑵.求证：2PDPBPA=•⑶.若PD＝4，1tan2CDB=，求直径AB的长．21.如图，点E是△ABC的内心，线段AE的延长线交BC于点F(∠AFC≠90°)，交△ABC的外接圆于点D.(1)求点F与△ABC的内切圆⊙E的位置关系；(2)求证：ED＝BD；(3)若∠BAC＝90°，△

ABC的外接圆的直径是6，求BD的长；(4)B，C，E三点可以确定一个圆吗？若可以，则它们确定的圆的圆心和半径分别是什么？若不可以，请说明理由．1618.如图，在△ABC中，AB＝AC＝10，以AB为直径的⊙O与BC交于点D，与AC交于点E，连接OD，BE，它们交于点M，且MD＝2，则BE

的长为________.21．（14分）如图,在☉O上位于直径AB的异侧有定点C和动点P,AC=AB,点P在半圆弧AB上运动(不与A,B两点重合),过点C作直线PB的垂线CD交PB于点D.(1)如图1,求证:△PCD∽△ABC.(2

)当点P运动到什么位置时,△PCD≌△ABC?请在图2中画出△PCD,并说明理由.(3)如图3,当点P运动到CP⊥AB时,求∠BCD的度数.25.（10分）如图,点A是半径为6cm的☉O上的定点,动点P从A出

发,以πcm/s的速度沿圆周按顺时针方向运动,当点P回到A时立即停止运动.设点P运动时间为t(s),如果点B是OA延长线上的一点,且AB=AO,问t为多少时,△POB为直角三角形?请说明理由.1725．如

图①，在△ABC中，以AB为直径的⊙O交AC于点D，点E在BC上，连接BD，DE，∠CDE＝∠ABD．（1）求证：DE是⊙O的切线．（2）如图②，当∠ABC＝90°时，线段DE与BC有什么数量关系？请说明理由．（3）如图③，若AB＝AC＝10，sin∠CDE＝35，求BC的长．例3

如图8-4已知：在△ABC中，以AC边为直径的⊙O交BC于点D，在劣弧⌒AD上到一点E使∠EBC=∠DEC，延长BE依次交AC于G，交⊙O于H.(1)求证：AC⊥BH；(2)若∠ABC=45°，⊙O的直径等于10，BD=8，求CE的长.【分析】(1)连接

AD构造直角三角形，同时可以根据圆周角定理得到∠DEC=∠DAC，然后由∠EBC=∠DEC可得∠EBC=∠DAC.然后可由∠DAC+∠ACD=90°．可得∠EBC+∠ACD=90°，即AC⊥BH.(2)可由∠ABC=45°得△A

BD是等腰直角三角形，AD=BD=8,然后求的AC=6.再根据△CDE∽△CEB求得CE长度.【解】证明：(1)如图8-5连接AD∵∠DAC=∠DEC∠EBC=∠DEC∴∠DAC=∠EBC又∵AC是⊙O的直径∴∠ADC

=90°∴∠DCA+∠DAC=90°∴∠EBC+∠DCA=90°∴∠BGC=180°-(∠EBC+∠DCA)=180°-90°=90°∴AC⊥BH(2)法一：∵∠BDA=180°−∠ADC=90°，∠ABC=45°∴∠BAD=45°

．∴BD=AD．∵BD=8，∴AD=8．又∵∠ADC=90°，AC=10，图8-4图8-518∴68102222=−=−=ADACDC.∴BC=BD+DC=8+6=14.∵∠EBC=∠DEC，∠ECD=∠BCE，∴△CDE∽△CEB.∴CDCECECB=即614CECE=．∴CE

=212.法二∵∠BDA=180°−∠ADC=90°，∠ABC=45°，∴∠BAD=45°.∴BD=AD.∵BD=8，∴AD=8．又∵∠ADC=90°，AC=10，∴68102222=−=−=ADACDC.∴BC=BD+DC=8+6=14

又∵∠BGC=∠ADC=90°，∠BCG=∠ACD，∴△BCG∽△ACD.∴ACBCDCCG=.∴10146=CG.∴542=CG.连接AE，∵AC是直径，∴∠AEC=90°.又∵EG⊥AC，∴△CEG∽△CAE.∴CECGACCE=.∴841054

22===CGACCE.∴21284==CE.25、如图，在平面直角坐标系中，直线y＝﹣2x+4与坐标轴交于A，B两点，动点C在x轴正半轴上，⊙D为△AOC的外接圆，射线OD与直线AB交于点E．（1）

如图①，若OE＝DE，求＝；（2）如图②，当∠ABC＝2∠ACB时，求OC的长；（3）点C由原点向x轴正半轴运动过程中，设OC的长为a，①用含a的代数式表示点E的横坐标xE；②若xE＝BC，求a的值．19