【文档说明】2024届高考一轮复习数学练习（新教材人教A版强基版）第七章 立体几何与空间向量 §7.9　空间距离及立体几何中的探索问题 Word版.docx，共(3)页，271.755 KB，由小赞的店铺上传

转载请保留链接：https://www.doc5u.com/view-1d6e54839d4cdc7068d440ae4bcaf7a6.html

以下为本文档部分文字说明：

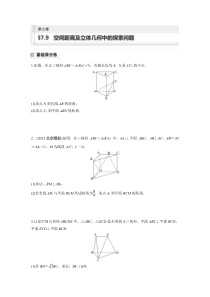
1.如图，在正三棱柱ABC－A1B1C1中，各棱长均为4，N是CC1的中点．(1)求点N到直线AB的距离；(2)求点C1到平面ABN的距离．2．(2023·北京模拟)如图，在三棱柱ABC－A1B1C1中，AA1⊥平面ABC，AB⊥AC，AB＝

AC＝AA1＝1，M为线段A1C1上一点．(1)求证：BM⊥AB1；(2)若直线AB1与平面BCM所成的角为π4，求点A1到平面BCM的距离．3.已知空间几何体ABCDE中，△ABC，△ECD是全等的正三角形，平面ABC⊥平面BCD，平面EC

D⊥平面BCD.(1)若BD＝2BC，求证：BC⊥ED；(2)探索A，B，D，E四点是否共面？若共面，请给出证明；若不共面，请说明理由．4.如图所示，在三棱锥P－ABC中，底面是边长为4的正三角形，PA＝2，PA⊥底面ABC，点E，F分别为AC，PC的中点．(1)求证：平面BEF⊥平面PAC；

(2)在线段PB上是否存在点G，使得直线AG与平面PBC所成角的正弦值为155？若存在，确定点G的位置；若不存在，请说明理由．5.(2022·北京模拟)如图，在四棱锥P－ABCD中，平面PBC⊥平面ABCD.△P

BC是等腰三角形，且PB＝PC＝3.在梯形ABCD中，AB∥DC，AD⊥DC，AB＝5，AD＝4，DC＝3.(1)求证：AB∥平面PCD；(2)求平面APB与平面PBC夹角的余弦值；(3)棱BC上是否存在点Q到

平面PBA的距离为1010，若存在，求出CQCB的值；若不存在，说明理由．6.(2023·盐城模拟)如图，正方体ABCD－A1B1C1D1的棱长为2，E，F分别为BD和BB1的中点，P为棱C1D1上的动点．(1)是否存在点P，使得PE⊥平面EFC？若存在，求出满足条件时C1P的长度并证明；若

不存在，请说明理由；(2)当C1P为何值时，平面BCC1B1与平面PEF夹角的正弦值最小．