【文档说明】安徽省滁州市定远县育才学校2021届高三下学期开学考试数学（理）试题 PDF版含答案.pdf，共(13)页，357.120 KB，由小赞的店铺上传

转载请保留链接：https://www.doc5u.com/view-7f743afa12b36de359481ea6e9545dd9.html

以下为本文档部分文字说明：

安徽省滁州市定远县育才学校2021届高三下学期开学考试数学（理）试题本卷满分150分，考试用时120分钟。第I卷（选择题共60分）一、选择题(共12小题，每小题5分，共60分)1.已知全集U={-1,0,1,2,3,4}，集合2{|430}AxNxx

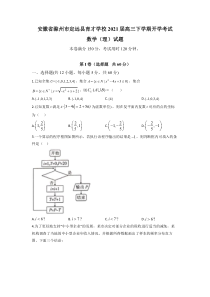
，集合2{|2}BxNyxx，则()UCAB（）A.{-1,0,1,2,3}B.{-1,0,4}C.{4}D.{-1,0,3,4}2.已知复数z满足(3425ziii为虚数单位)，则在复平面内复数z对应的点的坐标为（）A.21,5

B.2,15C.21,5D.2,153.一个算法的程序框图如图所示，若执行该程序输出的结果是1，则判断框内可填入的条件是（）A.6?iB.7?iC.7?iD.6?i4.为了更好地支持“中小型企

业”的发展，某市决定对部分企业的税收进行适当的减免，某机构调查了当地的中小型企业年收入情况，并根据所得数据画出了样本的频率分布直方图，下面三个结论：①样本数据落在区间[300500),的频率为0.45；②如果规定年收入在500万元以内的企业才能享受减免税政策，估计有55%的当地中小型企业能

享受到减免税政策；③样本的中位数为480万元.其中正确结论的个数为（）A.0B.1C.2D.35.函数f（x）＝2sin2（ωx﹣6）＞（ω＞0）的最小正周期为π．则f（x）在3,44上的

最小值是（）A.1+32B.12C.2D.1﹣326.已知函数200xxeexfxxx，若0.015a，33log22b，2log0.9c，则有（）A.

fbfafcB.fafbfcC.fafcfbD.fcfafb7.如图，点A的坐标为1,0，点C的坐标为2,4．函数2fxx，若在矩形ABCD内随机取一点．则该点取自阴影部分的概率为（）A.13B.12C.23D.512

8.在三棱锥PABC中，平面PAB平面ABC，25,6,3APABACB，且直线PA与平面ABC所成角的正切值为2，则该三棱锥的外接球的表面积为（）A.13B.52C.523D.521339.正项等比数列na中，225689264aaaa，且3a与7a的等

差中项为2，则1a（）A.325B.2C.25D.11710.已知'fx是函数fx的导函数，且对任意的实数x都有1'xfxfxe（e是自然对数的底数），00f，若不等式0fxk的解集中恰有两个整数，则实数k的取值范围是（）A.221,e

eB.3232,eeC.3232,eeD.3232,ee11.若函数()(1)(0xxfxkaaa且1a）在R上既是奇函数,又是减函数,则()log()agxxk的图象是（）A.B.C.D.12.已知函数1,(0)

()ln2,(0)xxexfxxxx，若函数yfxa至多有2个零点，则a的取值范围是（）A.1,1eB.1,1(1,)eC.11,1eD.[1,1]e第II卷（非选择题90分）二、填空题(共4

小题,每小题5分,共20分)13.已知单位向量12,ee的夹角为3，若向量122ee与向量122eke的夹角为2，则实数k________.14.函数f（x）＝22,0ln,0xxxxx

，则f（f（1e））＝_____.15.已知双曲线2222:1,0xyCabab的左、右焦点为1F、2F，点2F关于一条渐近线的对称点在另一条渐近线上，则双曲线C的离心率是________．16.四棱锥SABCD中，底面ABCD是边长为2的正方形，

侧面SAD是以SD为斜边的等腰直角三角形，若224SC，则四棱锥SABCD的体积取值范围为_____．三、解答题(共6小题,共70分。需给出必要的演算步骤。)17.（本小题满分12分）已知ABC中三个

内角A，B，C满足2cossin()1BAC．（1）求sinB；（2）若2CA，b是角B的对边，3b，求ABC的面积．18.（本小题满分12分）某芯片公司为了制定下一年的某种产品研发投入计划，需要了

解年研发资金投入量x（单位：亿元）对年销售额y（单位：亿元）和年收益z（单位：亿元）的影响，为此收集了近12年的年研发资金投入量ix和年销售额iy的数据并对这些数据作了初步处理，得到了下面的散点图及一些统计量的值.为了进一步了解年研发资金投

入量x对年销售额y的影响，公司三位员工查阅大量资料，对历史数据进行对比分析，分别提出了三个回归方程模型：①yabx；②2ycdx；③gxyfe.xy1221iixx121iiixxyy1221iiyy40667702

50200u1221iiuu121iiiuuxxv1221iivv121iiivvyy3.600.499.8065.0030.00表中lniiuy，2iivx.（1）根据散点图及表中数据，请分别选用两个比较恰

当的回归方程模型，建立y关于x的回归方程；（2）①根据（1）的回归方程模型，从数据相关性的角度考虑，判断哪一个更适宜作为年销售额y关于年研发资金投入量x的回归方程？并说明理由；②已知这种产品的年收益z服正态分布(40,204.75)N

，那么这种产品的收益超过54.31亿元（含54.31亿元）的概率为多少？附：①最小二乘估计以及相关系数公式：11222111ˆˆˆ,,nniiiiiinnniiiiiixxyyxxyybaybxrxxxxyy

；②若2~,zN，则有()0.6826Pz，(22)0.9544Pz；③参考数据：21.41,103.16,204.7514.31.19.（本小题满分12分）如图，在四棱锥

EABCD中，ADCD，2DADCDE，22EAEC，M是EA的中点.（1）证明：AE⊥平面MCD；（2）若//CDAB，三棱锥MBCE的体积为13，求底棱AB的长.20.（本小题满分12分

）已知椭圆221:163xyC的焦点与抛物线22:20Cxpyp的焦点之间的距离为2.（1）求抛物线2C的方程；（2）设1C与2C在第一象限的交点为A，过点A斜率为0kk的直线1l与1C的另一个交点为B，过点A与1l垂直的直线2l与2C的另一个交点为C.设ABmAC

，试求m的取值范围.21.（本小题满分12分）已知函数ln1fxxkx，（1）讨论函数fx的单调区间；（2）若对于任意的0x，不等式877xfxkxe，恒成立，求k的范围.四、选考题22.（本小题满分10分）选

修4-4:坐标系与参数方程在直角坐标系xOy中，P（0，1），曲线C1的参数方程为31232xtyt（t为参数）．以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为4cos．（1）求曲线C1的普通方程和C2的直角坐标方程；（2）曲线C1

与C2交于M，N两点，求||PM|﹣|PN||．参考答案1.B2.B3.D4.D5.D6.B7.D8.B9.C10.D11.A12.B13.8514.115.216.438,3317.（1）13（2）322解：（

1）在ABC中，ABC，即()BAC，∴sinsin()BAC，由题意得2cossin1BB．两边平方可得222cossin2sin1BBB，根据22sincos1BB，可整理为23sin2sin10BB

，解得1sin3B或sin1B（舍去）．∴1sin3B．（2）由2CA，且ABC，可得22AB，C为钝角，∴sin2cosAB，又3b，由正弦定理得33sinsinsinabcABC

，∴33sinaA，33sincC．又C为钝角，由（1）得cos223B．∴ABC的面积为111sin33sin33sin223SacBAC99sinsinsincos222AAAA9992232s

in2cos44432AB综上所述，ABC的面积为322．18.（1）选用②，③两个回归方程模型；22306yx，0.0133.08xye；（2）①模型②更适宜作为收益y关于投入量x的回归方程；答案见

解析；②0.1587.【解析】（1）因为散点图中x与y之间不是线性关系，故可以判断模型①不适合.故选用②，③两个回归方程模型.令2vx，先建立y关于v的线性回归方程：设y关于v的线性回归方程为ydvc.由于1211221()

()()iiiiivvyydvv30.0065.00，666630cydv，所以y关于u的线性回归方程为306yv，因此模型②为22306yx；由gxyfe，得lnlnygxf，令ln,,lnuygf

，所以ux，先建立u关于x的线性回归方程.由于1211221()()9.800.013770()iiiiiuuxxxx，3.60.013403.08ux，

所以u关于x的线性回归方程为0.0133.08ux，因此模型③为0.0133.08xye；（2）①模型②中，相关系数121212122211()()30.003100.33.160.948105200()()iiiiiiivvyyrvvyy

，模型③中，相关系数121312122211()()9.800.5050.49770()()iiiiiiiuuxxruuxx，可得321rr，说明变量y与v的线性相关程度更好，即模型②：22306yx拟合效果更好，故模型②更适宜作为收益y

关于投入量x的回归方程.②依题意z服从正态分布2(40,204.75)(40,14.31)NN，所以()(25.6954.31)0.6826PzPz，所以10.6826(54.31)0.15872Pz.19.解：（1）∵ADCD，2DADC，∴22

AC，又∵22EAEC，∴AEC为等边三角形，又∵2DADE，M是EA的中点∴AEDM，AEMC，2DM又∵DMMCM，,DMMC平面MDC∴AE⊥平面MCD；（2）∵AE⊥平面MCD，∴AECD，又∵ADCD，ADAE

A，,ADAE平面ADE∴CD平面ADE，又∵DM平面ADE，∴CDDM，∵//CDAB，∴ABDM，又∵AEDM，ABAEA，,ABAE平面ABE，∴DM平面ABE∵//CDAB∴C点到平面ABE的距离等于D点到平面ABE的距离∴MB

CECBMEDBMEVVV，又∵11113332DBMEBMEBMEABEVSDMSDMSDM11112223223AB，解得：1AB.20.（1）24

xy；（2）10,2.【解析】（1）由椭圆221:163xyC，得26a，23b，3c，所以，椭圆1C的右焦点为3,0F，抛物线22:20Cxpyp的焦点为0,2pF，由题意可得223

0022pFF，0p，2p，因此，抛物线2C的方程为24xy；（2）联立椭圆1C和抛物线2C的方程22216340xyxyx，解得21xy，可得点2,1A

，设点11,Bxy、22,Cxy，联立直线1l与椭圆1C的方程2216312xyykx，消去y得，22214218840kxkkxkk，由题意可知，2是关于x的二次方程22214218840kxkkxkk的一个根，由韦达

定理得212884221kkxk，21244221kkxk，22124111221kkABkxk，直线2l的方程为112yxk，联立直线2l与抛物线2C的方程21124yxkxy

，消去y得24840xxkk，由题意可知，2是关于x的二次方程24840xxkk的一个根，由韦达定理得2824xk，242xk，22222411114124kkkACxkkkk，所以，222110,11222ABkmkACk

，因此，m的取值范围是10,2.21.解：（1）∵1111xkkfxxx，定义域为1,+若0k，则1()01xkfxx对1x成立，∴fx在区间1,+单调递增；若k0，

则()fx在区间1,1k单调递减，在区间1,+k单调递增.（2）原命题可化为0x，ln1710xkxxxe恒成立.取ln171xgxkxxxe，∴21171(),711xxkgxkeuxuxe

xx，∴00,00,07gguk.若7k，即070gk，∴存在1>0x使得1(0,)xx，()0ux，所以()gx在1(0,)x单调递减，又∵(0)0g，所以1(0,),()0xx

gx，∴()gx在1(0,)x单调递减，又∵(0)0g，∴1(0,),()0xxgx，不合题意，∴7k若0k，则2()70(1)xkuxex对0x成立，若07k，可知2()7(1)xkuxex在(0,)单调递增，

∴0x，()(0)70uxuk.∴7k时，0x，()0ux，∴()gx在(0,)单调递增，∴0x，()(0)0gxg，∴()gx在(0,)单调递增，∴0x，()(0)0gxg.综上，k

的范围为(,7].22.（1）10xy，2240xyx，（2）14解：（1）曲线C1的参数方程为31232xtyt（t为参数），消去参数t得普通方程为10xy，曲线C

2的极坐标方程为4cos，两边同乘以，得24cos，所以其直角坐标方程为2240xyx（2）曲线C1过点P（0，1），则其参数方程为22212xtyt，将其代入方程2240xyx得，22222()(1)4()0222

ttt，化简得223210324140tt，，设上式方程的根为12,tt，所以121232,1tttt，所以22121212()4(32)4114PMPNtttttt

