【文档说明】新教材数学人教A版必修第一册教案：5.4三角函数的图象与性质 5.4.1正弦函数、余弦函数的图象 含解析【高考】.doc，共(7)页，541.000 KB，由小赞的店铺上传

转载请保留链接：https://www.doc5u.com/view-70848c663ce37e4698ca533ddbea7b10.html

以下为本文档部分文字说明：

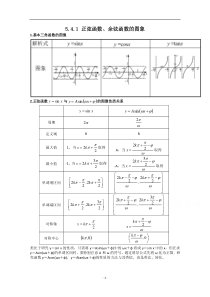
-1-5.4.1正弦函数、余弦函数的图象1.基本三角函数的图像2.正弦函数xysin=与()+=xAysin的图像性质关系类比于研究y＝sinx的性质，只需将y＝Asin(ωx＋φ)中的ωx＋φ看成y＝sinx中的x，但在求y＝Asin(ωx＋φ)的单

调区间时，要特别注意A和ω的符号，通过诱导公式先将ω化为正数．研究函数y＝Acos(ωx＋φ)，y＝Atan(ωx＋φ)的性质的方法与其类似，也是类比、转化．xysin=()+=xAysin周期22定义域RR最大值1，当22+=kx取得A，当

−+=22kx取得最小值-1，当232+=kx取得-A，当−+=232kx取得单调增区间+−22,22kk−+−−22,22kk单调减区间++232,22kk−+−+

232,22kk对称轴2+=kx−+=2kx对称中心()0,k−0,k-2-3.余弦函数xycos=与()+=xAycos的图像性质关系xycos=()+=xAycos周期2

2定义域RR最大值1，当kx2=取得A，当−=kx2取得最小值-1，当+=kx2取得-A，当−+=kx2取得单调增区间kk2,2−−−−kk2,2单调减区间+kk2,2−+−kk2,2对称轴kx=

−=kx对称中心+0,2k−+0,2k-3-例1：函数y=2sin（3x+），x∈R的最小正周期是（）A．B．C．D．π解：223T==,故选B。例2：已知函数f（x）=sin（ωx+）（ω＞0）的最小正周期为π，则函数f（x）的图象（

）A．关于直线x=对称B．关于直线x=对称C．关于点（，0）对称D．关于点（，0）对称解：由函数f（x）=sin（ωx+4）（ω＞0）的最小正周期为π，可得2T==求得ω=2，f（x）=sin（2x+4）．由于当228kxk

+−==+时，函数f（x）取得最大值为1，故函数f（x）的图象关于直线8x=对称，故选：B．例3：设函数f（x）=Asin（ωx+φ）（A≠0，ω＞0，﹣的图象关于直线x=对称，它的最小正周期为π，则（）A．f（x）的图象过点B．f（x）在上是

减函数C．f（x）的一个对称中心是D．f（x）的一个对称中心是解：由题意可得2T==，∴ω=2，可得f（x）=Asin（2x+φ）．再由函数关于23x=对称，故222326kkk+−+−===+，取6=，

故函数f（x）=Asin（2x+6）．根据公式−+−+232,22kk可求得函数的减区间为[kπ+6，kπ+23]，B错，由于A不确定，故选项A不正确．对称中心为−0,k，即（212k−，0），1k=时，选项C正确．选项D不正确．例

4：（2015•安徽）已知函数f（x）=Asin（ωx+φ）（A，ω，φ均为正的常数）的最小正周期为π，当x=时，函数f（x）取得最小值，则下列结论正确的是（）A．f（2）＜f（﹣2）＜f（0）B．f（0）＜f（2）＜f（﹣2）C．f（﹣2）＜f（0）＜f（2）D．f（2）＜f（0）＜

f（﹣2）解：依题意得，函数f（x）的周期为π，∵ω＞0，∴2T==，∴ω=2，又∵当23x=时，函数f（x）取得最小值，33222222326kkk+−+−===+-4-∴f（x）=A

sin（2x+2kπ+6）=Asin（2x+6）．∴f（﹣2）=f（﹣2+2π），f（2）=f（π+2）=Asin（4+6）＜0，f（0）=f（）＞0，根据公式−+−+232,22kk可求得函数的减区

间为[kπ+6，kπ+23]，又∵53＞π+2＞﹣2+2π＞76，∴f（2）＜f（﹣2）＜f（0）故选：A．例5：函数f（x）=2sin（2x+）在[﹣，]上对称轴的条数为（）A．1B．2C．3D．0解：226kkx+−==+，∵﹣2≤x≤2，∴函数的对称轴为：()(

)0;163xkxk===−=−，故选B。例6：函数y=2sin（3x﹣）的图象中两条相邻对称轴之间的距离是．解：两条相邻对称轴之间有半个周期，即12223T===。例7：同时具有性质①最小正周期是π；②图象关于直线x=对

称；③在[﹣，]上是增函数的一个函数是（）A．y=sin（+）B．y=cos（2x+）C．y=sin（2x﹣）D．y=cos（﹣）解：2T==求得ω=2，排除A、D，在B选项中，对称轴为直线,1

=263kkxkx−==−=当时，，单调增区间为222,,,36kkkk−−−−−不能满足题意，C选项中对称轴为直线+2+,0=233kkxkx−===当时，，单调增区间为2222,,,33kkkk

−−+−−+故选C。例8：函数y=sin（﹣2x+）的单调递增区间是（）A．[﹣+2kπ，+2kπ]（k∈Z）B．C．[﹣+kπ，+kπ]（k∈Z）D．解

：sin2sin266yxx=−+=−−，根据题意，只需求出sin26yx=−的单调减区间即可，322522,,36kkkk+−+−++，故答

案选D。-5-例9：设函数f（x）=sinωπx（ω＞0）的图象在区间[0，]上有两个最高点和一个最低点，则（）A．3≤ω＜5B．4≤ω＜6C．5≤ω＜7D．6≤ω＜8解：由题意，结合函数图像可知55

122572+，故选C。例10:已知函数sin()yAx=+（0,||A）的一段图象如下图所示，求函数的解析式．解：由图像可知，最大值为2，最小值为-2，故2A=图中已知的两点为24,xx，故可联立方程组232283348−=−=

−==32sin(2)4yx=+例11:已知函数sin()yAx=+在同一周期内，当9x=时，取得最大值12，当49x=时，取得最小值12−，则该函数的解析式是（）A.12sin()36yx=−B.1sin(

3)26yx=+C.1sin(3)26yx=−D.1sin(3)26yx=−+解：由题意可知，最大值为12，最小值为12−，故12A=，已知的两点为24,xx，故可联立方程组23239469−==

−==1sin(3)26yx=+选B。例12：若函数()2sin(2)6fxx=+，求()yfx=在0,2上的最大值和最小值．解：1234305222,,,1261

23xxxx−−−−==−======，则区间0,2包含2,6x=最大值为2，在0,6单调递增，在,62单调递减，由于递减区间宽度

大于递增区间宽度，故最小值为()2sin()126f=+=−（如图）。例13：如图所示，函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜）的部分图象，已知x1，x2∈（，π），且f（x1）=f（x2），则f（x1+x2）=（）秒杀秘籍:五点法求解三角函数图像（1）找到

相应的54321,,,,xxxxx中两点；（2）寻找两点联立方程−=−=−=−=−=2,,,,052343221xxxxx388−22−0-6-A．﹣1B．C．D．解：02633−=−=−==sin(

2)3yx=+，x1，x2∈（3，π），且f（x1）=f（x2），故121237722126xxxx−+==+=，()1283sin32fxx+==。例14：若函数，且f（α）=﹣2，f（β）=0，|α﹣β|的最小值是，则

f（x）的单调递增区间是（）A．B．C．D．解：由题意可知，最大值为2，最小值为2−，已知的两点为45,xx，故可联立方程组32323122−=−===−=2sin()

3yx=+故单调增区间为52,266kk−+选D。例15：如图是函数图象的一部分，对不同的x1，x2∈[a，b]，若f（x1）=f（x2），有，则φ的值为（）A．B．C．D．解：

()()121222kxxfxfx+−+==由图像可知：A=2，又()()122sin232sin323fxxfkk+=+−=+−===，选D。例16：（1）若函数()3cos()fxwx=+对任意的,()()66xRfxfx+=

−有，则()6f等于（）A．3−B．0C．3D．3（2）若()mxxf++=)cos(2，对任意实数t都有)()4(tftf−=+，且1)8(−=f，则实数m的值等于()A.±1B.±3C.－3或1D.－1或3定理：()()()faxfbxfx+=−关于直线2abx+=对称；()

()()faxfbxfx+=−−关于点,02ab+对称；解：（1）由题意可得：()fx关于直线6x=对称；故()63,Df=选（2）由题意可得：()fx关于直线8x=对称；故()82131,fmmm=+=−=−=或选C-7-例17：函数f（x）=sin（ωx+φ）

（ω，φ是常数，ω＞0）．若f（x）在区间[，1]上具有单调性，且f（0）=f（）=﹣f（1），则下列有关f（x）的每题正确的有（请填上所有正确命题的序号）．①f（x）的最小周期为2；②x=是f（x）的对称轴；③f（x）在[1，]上具有单

调性；④y=f（x+）为奇函数．()()21250=1,03336ffxff==−解：为对称轴；为对称中心；故②正确，56yfx=+表示将()yfx=向左移56个单位，即关于原点对称，故④正确，由于()yfx=在区间[13，1]上具有单

调性，故根据对称原理可得③正确；2132566T−===−==故①正确；答案为①②③④。