【文档说明】新教材数学人教A版必修第一册教案：5.4三角函数的图象与性质 5.4.1正弦函数、余弦函数的图象 含解析.doc，共(7)页，540.500 KB，由envi的店铺上传

转载请保留链接：https://www.doc5u.com/view-abcdcf5c97d3927224d34746074d185d.html

以下为本文档部分文字说明：

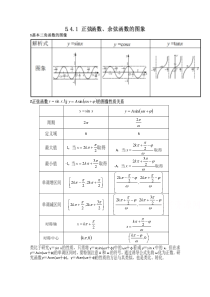
1.2.xysin=()+=xAysinysinxyAsin(ωxφ)ωxφysinxxyAsin(ωxφ)AωωyAcos(ωxφ)yAtan(ωxφ)xysin=()+=xAysin22RR122+=kxA−+=22kx-1232+=kx-A−

+=232kx+−22,22kk−+−−22,22kk++232,22kk−+−+232,22kk2+=kx−+=2kx()0,k−0,

k3.xycos=()+=xAycosxycos=()+=xAycos22RR1kx2=A−=kx2-1+=kx2-A−+=kx2kk2,2−−−−kk2,2+kk2,2−+−kk2

,2kx=−=kx+0,2k−+0,2k1y=2sin3x+x∈RABCDπ223T==,B2fx=sinωx+ω0πfxAx=Bx=C0D0fx=sinωx

+4ω0π2T==ω=2fx=sin2x+4228kxk+−==+fx1fx8x=B3fx=Asinωx+φA≠0ω0x=πAfxBfxCfxDfx2T==∴ω=2fx=Asin2x+φ23x=222326kk

k+−+−===+6=fx=Asin2x+6−+−+232,22kk[kπ+6kπ+23]BAA−0,k212k−01k=CD42015•fx=Asinωx+φAωφπx=fxA

f2f2f0Bf0f2f2Cf2f0f2Df2f0f2fxπ∵ω0∴2T==∴ω=2∵23x=fx33222222326kkk+−+−===+∴fx=Asin2x+2kπ+6=Asin2x+6∴f2=f2+2πf2=fπ+2

=Asin4+60f0=f0−+−+232,22kk[kπ+6kπ+23]∵53π+22+2π76∴f2f2f0A5fx=2sin2x+[]A1B2C3D0226kkx+−==+∵2≤x≤2∴()

()0;163xkxk===−=−B6y=2sin3x12223T===7①π②x=③[]Ay=sin+By=cos2x+Cy=sin2xDy=cos2T==ω=2ADB,1=263kkxkx−==−=222,,,

36kkkk−−−−−C+2+,0=233kkxkx−===2222,,,33kkkk−−+−−+

C8y=sin2x+A[+2kπ+2kπ]k∈ZBC[+kπ+kπ]k∈ZDsin2sin266yxx=−+=−−sin26yx=−322522,,36

kkkk+−+−++D9fx=sinωπxω0[0]A3≤ω5B4≤ω6C5≤ω7D6≤ω855122572+Csin()yAx=+0,||A2A=24,xx232283348

−=−=−==32sin(2)4yx=+sin()yAx=+9x=1249x=12−A.12sin()36yx=−B.1sin(3)26yx=+C.1sin(3)26yx=−D.1sin(3)26yx=−+1212−12A=24

,xx23239469−==−==1sin(3)26yx=+12()2sin(2)6fxx=+()yfx=0,21234305222,,,126123xx

xx−−−−==−======0,22,6x=20,6,62()2sin()126f=+=−13fx=sinωx+φω0|φ|x1x2∈πfx1=fx2fx1+x2=秒杀秘籍:五点法求解三角函数图

像154321,,,,xxxxx2−=−=−=−=−=2,,,,052343221xxxxx388−22−0A1BCD02633−=−=−==sin(2)3yx=+x1x

2∈3πfx1=fx2121237722126xxxx−+==+=()1283sin32fxx+==14fα=2fβ=0|αβ|fxABCD22−45,xx32323122−=−

===−=2sin()3yx=+52,266kk−+D15x1x2∈[ab]fx1=fx2φABCD()()121222kxxfxfx+−+==A=2()()122sin232sin323fxxfkk

+=+−=+−===D161()3cos()fxwx=+,()()66xRfxfx+=−()6fA3−B0C3D32()mxxf++=)cos(2t)()4(tftf−=+1)8(−=fm()A.1B.3C.31D

.13()()()faxfbxfx+=−2abx+=()()()faxfbxfx+=−−,02ab+1()fx6x=()63,Df=2()fx8x=()82131,fmmm=+=−=−=17fx=sinωx+φωφω0fx[1]f0=f=f

1fx①fx2②x=fx③fx[1]④y=fx+()()21250=1,03336ffxff==−②56yfx=+()yfx=56④()yfx=[131]③2132566T−==

=−==①①②③④