【文档说明】西藏自治区拉萨中学2020-2021学年高二下学期第七次月考数学（文）试题含答案.doc，共(21)页，1.340 MB，由小赞的店铺上传

转载请保留链接：https://www.doc5u.com/view-3e47c6074704c468a3e4e46c9820bbe3.html

以下为本文档部分文字说明：

拉萨中学高二年级（2022届）第七次月考文科数学试卷（满分：150分，考试时间：120分钟。请将答案填写在答题卡上）第I卷（选择题，共60分）一、单选题:本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合{1,2,3},{2,

3,5}AB==，则（）A．1,2,3,5AB=B．{2,3}AB=C．ABD．5AB2．复数51izi+=−，则z的共轭复数z=（）A．23i+B．23i−C．33i+D．33i−3．空气质量A

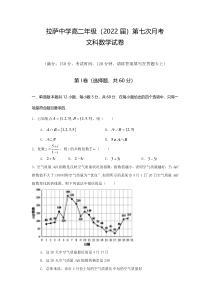
QI指数是反映空气质量状况的指数，指数值越小，表明空气质量越好，当AQI指数值不大于100时称空气质量为“优良”.如图所示的是某市4月1日~20日空气质量AQI指数变化的折线图，则下列说法中错误的是（）A．这20天中空气质量最好的是4月17日B．这20天空气质量AQI指数的极差是240C．总体来说

，该市4月份上旬的空气质量比中旬的空气质量好D．从这20天的空气质量AQI指数数据中随机抽出一天的数据，空气质量为“优良”的概率是0.54．设xR，则“230xx−”是“12x”的（）A．充要条件B．充分不必要条件C．必要不充分条件D．既不充分也不必要条件5.曲线f(x)

=2xx+在点(-1，-1)处的切线方程为（）A．y=2x+1B．y=2x-1C．y=-2x-3D．y=-2x-26．把函数()yfx=图像上所有点的横坐标缩短到原来的12倍，纵坐标不变，再把所得曲线向右平移3个单位

长度，得到函数sin4yx=−的图像，则()fx=（）A．7sin212xx−B．sin212x+C．7sin212x−D．sin212x+7．已知m，n为两条不重合的直线

，，为两个不重合的平面，则下列命题中正确的是（）A．若//m，n//，⊥，则mn⊥B．若mn⊥，n⊥，⊥，则m⊥C．若//m，n，则m与n异面D．若m⊥，n⊥，//mn，则//8．若,xy满足约束条件4,2,3,xy

xyy+−则3zxy=+的最小值为（）A．18B．10C．6D．49．从分别写有“1，2，3，4，5”的5张卡片中，随机抽取一张不放回，再随机抽取一张，则抽得的两张卡片上的数字一个是奇数一个是偶数的概率是（）A．

45B．35C．25D．31010．为了测量某种海鱼死亡后新鲜度的变化.研究人员特意通过检测该海鱼死亡后体内某微量元素的含量来决定鱼的新鲜度.若海鱼的新鲜度h与其死亡后时间t(小时)满足的函数关系式为1thm

a=−.若该种海鱼死亡后2小时，海鱼的新鲜度为80%，死亡后3小时，海鱼的新鲜度为60%，那么若不及时处理，这种海鱼从死亡后大约经过（）小时后，海鱼的新鲜度变为40%.(参考数据：ln20.7，ln31.1)A．3.3B．3.6C．4D．

4.311.若2510ab==，则11ab+=（）A．1−B．lg7C．1D．7log1012．已知1F，2F是椭圆C：22194xy+=的两个焦点，点M在C上，则12MFMF的最大值为（）A．13B．12C．9D．6第II卷（非选择题）二、填空题：本题共4小题，每

小题5分，共20分．13．向量(1,2)a=，(,1)bx=.若()()abab+⊥−，则x=____________14．《九章算术》是中国古代张苍、耿首昌所撰写的一部数学专著，被誉为人类科学史上应用数学的最早巅峰.全书分为九章，卷第六“均输

”有一问题：“今有竹九节下三节容量四升，上四节容量三升问中间二节欲均容各多少?”其意思为：“今有竹9节，下3节容量4升，上4节容量3升，使中间两节也均匀变化，每节容量是多少?”这一问题中从下部算起第5节容量是_________________升.(结果保留分数)15．已

知1tan3=−，则1cos2−=______．16．已知双曲线C：2222xyab−＝1（a＞0，b＞0）的左焦点为F，过F作C的一条渐近线的垂线l，垂足为A，l与C的另一条渐近线的交点为B，若A是线段FB的中点，则双曲线C的离心率为__．三、解答题：共70分．解答应写

出文字说明、证明过程或演算步骤．第17~21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．17．已知在等差数列{}na中，nS为其前n项和，且375,49aS＝＝.（1）求数列{}na的通项公式；（2）若2

,nannba+＝数列{}nb的前n项和为,nT求,nT.18．第五代移动通信技术简称5G或5G技术，是最新一代蜂窝移动通信技术，也是继4G系统之后的延伸.为了了解市民对A，B运营商的5G通信服务的评价，分别从A

，B运营商的用户中随机抽取100名用户对其进行测评，已知测评得分在70分以上的为优秀，测评结果如表：A运营商的100名用户的测评得分：得分[40，50](50，60](60，70](70，80](80，90](90，100]频率0.180.2

30.30.240.030.02（1）根据频率分布直方图，分别求出B运营商的100名用户的测评得分的中位数和平均值(同一组中的数据用该组区间的中点值为代表)；（2）填写下面列联表，并根据列联表判断是否有99%的把握认为测评得分是否优秀与运营商有关？优秀非优秀合

计A运营商B运营商合计附：22()()()()()nadbcKabcdacbd−=++++，其中nabcd=+++.P(K2≥k0)0.1000.0500.0250.0100.001k02.7063.8415.0246.63510.82819．如图，在直四棱柱1111A

BCDABCD−中，底面ABCD为菱形，E为1DD中点.（1）求证：1//BD平面ACE；（2）求证：1BDAC⊥.20．已知抛物线1C：22ypx=(0p)的焦点与双曲线2C：221412xy−=右顶点重合.（1）求抛物线1C的标准方程；（2）设过点()0,1的直线l与抛物

线1C交于不同的两点A，B，F是抛物线1C的焦点，且1FAFB=，求直线l的方程.21．已知函数()ln2fxxxax=−+（a为实数）（1）若2a=，求()fx在21,e的最值；（2）若()0fx恒成立，求

a的取值范围．选考题，共10分．请考生在第22、23题中任选一题作答．如果多做，则按所做的第一题计分．22．在平面直角坐标系xOy中，曲线C的参数方程为2cossinxy==（为参数），直线l的参数方程为223xtyt=+=+（t为参数）．（1）求直线l的普通

方程；（2）设()2,3A，若直线l与曲线C相交于P，Q两点，求11APAQ+的值．23．已知函数()41fxxx=−+−.(1)解不等式()4fx；(2)若方程()10fxkx−−=的解集为空集，求k

的取值范围参考答案1D【分析】利用集合的交、补运算判断A、B，进而由元素与集合的关系判断D的正误，根据已知集合判断A、B是否有包含关系.【详解】A：{1,2,3}{2,3,5}{2,3}AB==，错误；B：{1,2,3}{2,3,5}{1

,2,3,5}AB==，错误；C：,AB没有包含、被包含关系，错误；D：由A知：5AB，正确.故选：D.2．B【分析】利用复数的除法运算化简为标准形式，进而根据共轭复数的定义得解.【详解】()()()()51546231112iiiiziiii++++====+−−+,z

=23i−,故选：B.3．C【分析】根据折线图可确定4月17日质量AQI指数，即可判定选项A；求出这20天天气质量AQI指数的最大值和最小值，即可判定选项B；根据折线图中的数据，即可判定选项C；求出空气质量为“优良

”的天数，由古典概型公式求出其概率，即可判定选项D.【详解】由折线图可知4月17日质量AQI指数为20，是这20天中的最低，选项A正确；由折线图可知这20天中天气质量AQI指数的最大值是260，最小值是20，极差为240，选项B正确；根据折线图

前10天的天气质量AQI指数高于后10天，选项C错误；由折线图可知这20天中空气质量为“优良”天数为10天，所以空气质量为“优良”的概率是0.5，选项D正确.故选：C.4．C【分析】根据一元二次不等式的解法，结合充分性、必要性的定义进行判断即可.【详解】由23003xxx−，由03x

不一定能推出12x，但是由12x一定能推出03x，所以“230xx−”是“12x”的必要不充分条件，故选：C5A【分析】对函数f(x)求导，再算出导函数在x=-1时的值，得切线斜率于是得解.【详解】221(2)12()(2)(2)xxfxxx+−==++，曲线f

(x)=2xx+在点(-1，-1)处的切线斜率(1)2kf=−=，曲线f(x)=2xx+在点(-1，-1)处的切线方程为y+1=2(x+1)，即y=2x+1.故选：A6．B【分析】解法一：从函数()yfx=的图象出发，按照已知

的变换顺序，逐次变换，得到23yfx=−，即得2sin34fxx−=−，再利用换元思想求得()yfx=的解析表达式；解法二：从函数sin4yx=−出发，逆向实施各步变换，

利用平移伸缩变换法则得到()yfx=的解析表达式.【详解】解法一：函数()yfx=图象上所有点的横坐标缩短到原来的12倍，纵坐标不变，得到(2)yfx=的图象，再把所得曲线向右平移3个单位长度，应当得到23yfx=−

的图象，根据已知得到了函数sin4yx=−的图象，所以2sin34fxx−=−，令23tx=−,则,234212ttxx=+−=+,所以()sin212tft=+

,所以()sin212xfx=+；解法二：由已知的函数sin4yx=−逆向变换，第一步：向左平移3个单位长度，得到sinsin3412yxx=+−=+的图象，第二步：图象上所有点的横坐标伸长到

原来的2倍，纵坐标不变，得到sin212xy=+的图象，即为()yfx=的图象，所以()sin212xfx=+.故选：B.【点睛】本题考查三角函数的图象的平移和伸缩变换，属基础题，可以正向变换，也可以逆向

变换求解，关键是要注意每一步变换，对应的解析式中都是x的变换，图象向左平移a个单位，对应x替换成xa+,图象向右平移a个单位，对应x替换成xa−,牢记“左加右减”口诀；图象上每个点的横坐标伸长或缩短到原来的k倍，对应解析式中x替换成xk.7．D【分析】直接利用线面平行和线面垂直的判定和

性质，以及面面平行和面面垂直的性质，逐项判定，即可求解.【详解】由题意，直线,mn为两条不重合的直线，,为两个不重合的平面，对于A中，若//m，n//，⊥，可能//mn，所以A不正确；对于B中，若mn

⊥，n⊥，⊥，可能//m，所以B不正确；对于C中，若//m，n，则m与n异面或//mn，所以C不正确；对于D中，由m⊥，//mn，可得n⊥，又由n⊥，所以//，所以D正确.故选：D8．C【分析】由题意作出

可行域，变换目标函数为3yxz=−+，数形结合即可得解.【详解】由题意，作出可行域，如图阴影部分所示，由43xyy+==可得点()1,3A,转换目标函数3zxy=+为3yxz=−+，上下平移直线3yxz=−+，数形结合可得当直线过点A时,z取最小值，此时min3136z=+=.故选：C

.9．B【分析】根据题意，列出所有可能结果，结合古典概率计算即可.【详解】根据题意可知，所有抽取结果如下：（1，2），（2，1），（3，1），（4，1），（5，1），（1，3），（2，3），（3，2），（4，2），（5，2），（1，4），（2，4），（3

，4），（4，3），（5，3），（1，5），（2，5），（3，5），（4，5），（5，4），共20种结果，其中两张卡片上的数字一个是奇数一个是偶数有12种，故抽得的两张卡片上的数字一个是奇数一个是偶数的概率为1

23205=.故选：B.10．B【详解】由题思可得：()()23210.8310.6hmahma=−==−=，解得2a=，0.05m=，所以()10.052tht=−.令()10.0520.4tht=−=，可得212t=，两边问时取对数，故ln122ln2ln33.6l

n2ln2t+==小时，故选B.11C【分析】由已知表示出,ab，再由换底公式可求.【详解】2510ab==，25log10,log10ab==，251111lg2lg5lg101log10log10ab+=+=+==.故选：C.12．C【分析】本题通过利

用椭圆定义得到1226MFMFa+==，借助基本不等式212122MFMFMFMF+即可得到答案．【详解】由题，229,4ab==，则1226MFMFa+==，所以2121292MFMFMFMF+=

（当且仅当123MFMF==时，等号成立）．故选：C．13．2x=【分析】由()(1,3)abx+=+，()(1,1)abx−=−，由()()abab+⊥−可得()()0abab+−=带入即可得解.【详解】()(1,3)abx+=+，()(1,1)abx−=−，22()()(1)(1)

31340ababxxxx+⊥−=−++=−+=−=，所以2x=，故答案为：2.14．6766【分析】记从下部算起第n节的容量为na，可知数列na为等差数列，利用等差数列通项公式可构造关于1,ad的方程组，解方程组求得1,ad后，利用通项公式可求得5a.【详解】记从下部算起第n节的容量为n

a，由题意可知：数列na为等差数列，设其公差为d，则1231678913344263aaaadaaaaad++=+=+++=+=，解得：19566766ad==−，5167466aad=+=，即从下部算起第5节容量是6766升.故答案为：6766.15．15【分析】利

用二倍角公式化简目标，利用齐次式可得结果.【详解】∵1tan3=−，∴22222222sin2tan191cos22sin1sincostan1519−=====+++，故答案为：1516．2【分析】先设直线l，再与一条直线联立求点A

的坐标，然后根据中点得点B的坐标，再代入另一条渐近线方程中，可得224ca=即可求离心率.【详解】解：双曲线C：2222xyab−＝1（a＞0，b＞0）的左焦点为F（﹣c，0），过F作C的一条渐近线的垂线l，垂足为A，所以AF的方程为：y＝()axcb+，与bx+ay＝0联立，可得2(a

Ac−，)abc，l与C的另一条渐近线的交点为B，若A是线段FB的中点，可得B（222cac−，2abc），代入bx﹣ay＝0，可得：c2＝4a2，则双曲线C的离心率为e＝2．故答案为：2．17．（1）21nan=−；（2）6n，nZ.【分析】（1

）由条件求得公差，写出通项公式；（2）求出nb通项公式，利用分组求和求得nT，且单增，找到符合1000nT的最小n值即可.【详解】（1）由等差数列性质知，74749Sa=＝，则47a=，故公差43752daa=−=−=，1321aad=−=故21nan=−（2）由（1）知2

1221nnbn−+−＝，13212123221nnTn−=++++++−1321222(1321)nn−=+++++++−12121222(121)2214233nnnnn++−+−=+=+−−易知nT单调递增，且57071000T=，627661000T=，故10

00nT，解得6n，nZ.18．（1）中位数为70，平均值为69.2；（2）答案见解析.【分析】（1）由频率分布直方图即可求出中位数和平均值；（2）根据频率分布表和直方图求出优秀和非优秀数量即可得出列联表，求出卡方值即可判断.【详解】（1）由频率分布直方

图可知B运营商测评得分在区间[40,70]的频率为(0.0080.0160.026)100.5++=，故B运营商测评得分的中位数为70；由频率分布直方图可知B运营商测评得分的平均值为450.08550.16650.26750.38

50.16950.0469.2+++++=；（2）由频率分布表可知A运营商测评得分优秀的有100(0.240.030.02)29++=个，非优秀的有100(0.180.230.3)71++=个，由频率分布直方图可知B运营商测评得分优秀的有(0.030.0160.00

4)1010050++=个，非优秀的有(0.0080.0160.026)1010050++=个，则可得列联表如下：优秀非优秀合计A运营商2971100B运营商5050100合计79121200则22200(29507150)9.2276.6351001007

9121K−=，所以有99%的把握认为测评得分是否优秀与运营商有关.19．（1）证明见解析；（2）证明见解析；【分析】（1）设AC与BD交于点O，接OE，可得1//OEDBB，即可证明1//BD平面ACE；（2）由底面ABCD是菱形，得ACBD⊥，又1DD⊥底面ABCD，可

得1DDAC⊥，证明AC⊥平面11BDBD，利用线面垂直的性质可证1ACBD⊥．【详解】证明：（1）设AC与BD交于点O，接OE，底面ABCD是菱形，O为DB中点，又因为E是1DD的中点，1//OEDBB，OE面AEC，

1BD平面AEC1//BD平面ACE．（2）底面ABCD是菱形，ACBD⊥，1DD⊥Q底面ABCD，AC底面ABCD，1DDAC⊥，且1DBDDD=，1,DBDD平面11BDBD．AC⊥平面11BDBD．1BD平面11BDBD，1ACB

D⊥．20．（1）28yx=；（2）1yx=+或51yx=−+.【分析】（1）由双曲线和抛物线的几何性质，即可求解；（2）设()11,Axy，()22,Bxy及直线l的方程，与抛物线C的方程联立，由判别式､韦达定理得出12xx+，12xx，结合已知条件求出k的值，即可求得

直线l的方程.【详解】（1）由题设知，双曲线222:1412xyC−=的右顶点为()2,0，∴22p=，解得4p=，∴抛物线1C的标准方程为28yx=.（2）设()11,Axy，()22,Bxy，显然直线l的斜率存在，

故设直线l的方程为1ykx=+，联立218ykxyx=+=，消去y得()222810kxkx+−+=，由0得()222840kk−−，即2k，∴12228kxxk−+=−，1221xxk=.又∵1FAFB=，()2,0F，∴()

()1212221FAFBxxyy=−−+=，∴()()()()()()2121212121224111251xxxxkxkxkxxkxx−+++++=++−++=，即2450kk+−=，解得1k=或5k=−，∴直线l的方程为1yx=+或51yx=−+.21

．（1）2e−；（2）(,1ln2−+．【分析】（1）首先求函数的导数，判断函数的单调性，再根据最值的定义，求解函数的最值；（2）首先参变分离为2lnxax+恒成立，利用导数求()2lngxxx=+的最小值，即可求得a的取值范围.【详解】（1）当2a=时，()ln22fx

xxx=−+，()ln1fxx=−由()0fx得0xe﹐由()0fx得xe，所以()fx在()0,e上单调递减，在()e,+上单调递增，且()eelne2e22ef=−+=−()11ln12120f=−+=()2222ln222fe

eee=−+=则函数()fx的最小值为2e−，最大值为2．（2）由题得0x，若()0fx恒成立，则ln20xax−+，即2lnxax+恒成立令()2lngxxx=+，则()22122xgxxxx−=−=，当02x时，()0gx；当2x时，()0gx，所以()gx在()0,2

上单调递减，在()2,+上单调递增，则()()min21ln2gxg==+，所以1ln2a+，故a的取值范围为(,1ln2−+．22．（1）21yx=−；（2）13545．【分析】（1）消去参数t，即可得到直线的普通方程；（

2）首先求出曲线C的普通方程，再将直线的参数方程化为标准式，代入曲线C中，利用直线参数方程参数t的几何意义计算可得；【详解】解：（1）因为直线l的参数方程为223xtyt=+=+（t为参数）．则2tx=−代入23yt=+得()223yx=−+所以直线l普通方程为21yx=−，（2）曲线C

的参数方程为2cossinxy==（为参数），曲线C的普通方程为2214xy+=，将直线l的参数方程化为125235xtyt=+=+，（t为参数）代入椭圆方程得：2175236055tt+

+=，12525175tt+=−，1236517tt=120tt，1t，2t同号，12121315145ttAPAQtt==++23．(1)19[,]22；(2)[)12,2−.【分析】(1)把函数()fx化为分段函数形式，在各段上解不等式即可作答；(2)

化方程为()1fxkx−=，作出函数()()1gxfx=−图象，利用数形结合的思想即可得解.【详解】(1)25,1()413,1?425,4xxfxxxxxx−+=−+−=−，则不等式()4fx化为：1254xx−+或1434x

或4254xx−，解得112x或14x或942x，即1922x，所以不等式()4fx的解集为19[,]22；(2)()10|4||1|1fxkxkxxx−−==−+−−，令()|4||1|1gxxx=−+−−方程()10fxkx−−=解集为空集，即直线y

kx=与函数()ygx=图象无公共点，在同一坐标系内作出直线ykx=和函数()ygx=图象，如图：直线ykx=是过原点的直线，当它过点A(4，2)时，12k=，当它与直线BC平行时，2k=−，观察图形知，当直线ykx=在直线12yx=和2yx=−所夹含x轴的对顶角区域(不包括直线1

2yx=)内绕原点旋转时与函数()ygx=图象无公共点，即122k−，所以k的取值范围是[)12,2−.