【文档说明】2024年新高考数学一轮复习题型归纳与达标检测 第03讲 不等关系与一元二次不等式（原卷版）.docx，共(5)页，333.043 KB，由小赞的店铺上传

转载请保留链接：https://www.doc5u.com/view-3387952edb8252063c67101d1e8b4186.html

以下为本文档部分文字说明：

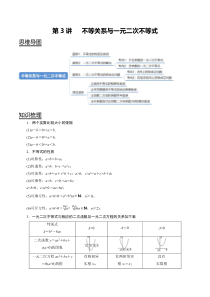
第3讲不等关系与一元二次不等式思维导图知识梳理1．两个实数比较大小的依据(1)a－b＞0⇔a＞b.(2)a－b＝0⇔a＝b.(3)a－b＜0⇔a＜b.2．不等式的性质(1)对称性：a>b⇔b<a；(2)传递性：a>b，b>c⇒a>c；(3)可加性：a>b⇔a＋

c>b＋c；a>b，c>d⇒a＋c>b＋d；(4)可乘性：a>b，c>0⇒ac>bc;a>b>0，c>d>0⇒ac>bd；(5)可乘方性：a>b>0⇒an>bn(n∈N，n≥1)；(6)可开方性：a>b>0⇒na>nb(n∈N，n≥2)．3．一元二次不等式与相应的二次函数及一元

二次方程的关系如下表判别式Δ＝b2－4acΔ>0Δ＝0Δ<0二次函数y＝ax2＋bx＋c(a>0)的图象一元二次方程ax2＋bx＋c＝0(a>0)的根有两相异实根x1，有两相等实根x1＝x2没有实数根x2(x1<x2)＝－b2aax2＋b

x＋c>0(a>0)的解集{x|x<x1或x>x2}{x|x≠x1}{x|x∈R}ax2＋bx＋c<0(a>0)的解集{x|x1<x<x2}∅∅核心素养分析用函数理解方程和不等式是数学的基本思想方法。本单元的学习，可以帮助学生用一元二次函数认识一元二次方程和一元二次不等式。通过梳理初中数

学的相关内容，理解函数、方程和不等式之间的联系，体会数学的整体性。题型归纳题型1不等式的性质及应用【例1-1】（2020春•湖北期中）下列命题中，正确的是()A．若acbc，则abB．若ab，cd

，则acbdC．若0ab，则22abD．若ab，cd，则acbd−−【跟踪训练1-1】（2020•玉溪二模）若01ba，1c，则()A．ccabB．ccabbaC．loglog

abccD．loglogabacbc【名师指导】比较大小的方法(1)作差法，其步骤：作差⇒变形⇒判断差与0的大小⇒得出结论．(2)作商法，其步骤：作商⇒变形⇒判断商与1的大小⇒得出结论．(3)构造函数法：构造

函数，利用函数单调性比较大小．(4)赋值法和排除法：可以多次取特殊值，根据特殊值比较大小，从而得出结论．题型2一元二次不等式的解法【例2-1】（2019秋•河东区期中）不等式28610xx−+的解集为．【例2-2】（2019·杭州模拟）求不等式12x2－ax>a2(a∈R)的解

集．【跟踪训练2-1】（2020春•启东市校级月考）一元二次不等式2260xx+−…的解集为()A．3(,2][,)2−−+B．3(,][2,)2−−+C．3[2,]2−D．3[,2]2−【跟

踪训练2-2】（2019秋•嘉兴期末）已知不等式20axbxc++的解集是{|}xx，0，则不等式20cxbxa++的解集是()A．11(,)B．(−，11)(，)+C．(

,)D．(−，](,)+【名师指导】1.解一元二次不等式的4个步骤2.解含参数的一元二次不等式的步骤(1)若二次项系数含有参数，则应讨论参数是等于0，小于0，还是大于0，然后将不等式转化为二次项系数为正

的形式；(2)判断方程根的个数，讨论判别式Δ与0的关系；(3)确定无根时可直接写出解集；确定方程有两个根时，要讨论两根的大小关系，从而确定不等式的解集．题型3一元二次不等式的恒成立或有解问题【例3-1

】（2020•一卷模拟）已知关于x的不等式2230axxa−+在(0，2]上有解，则实数a的取值范围是()A．3(,)3−B．4(,)7−C．3(,)3+D．4(,)7+【例3-2】（2018秋•凌源市期末）

不等式210xkx−+对任意实数x都成立，则实数k的取值范围是．【跟踪训练3-1】（2020春•湖北期中）若关于x的不等式210axax++„的解集为，则实数a的取值范围是()A．[0，4]B．(0,4)C．(−，0](4,)+D．[0，4)【跟踪训

练3-2】（2019秋•崇川区校级月考）关于x的不等式220xax+−在区间[1，4]上有实数解，则实数a的取值范围是.【名师指导】1.一元二次不等式恒成立的条件(1)ax2＋bx＋c>0(a≠0)恒成立的充要条件是

a>0，b2－4ac<0.(2)ax2＋bx＋c<0(a≠0)恒成立的充要条件是a<0，b2－4ac<0.2.一元二次不等式在给定区间上的恒成立问题的求解方法(1)若f(x)>0在集合A中恒成立，

即集合A是不等式f(x)>0的解集的子集，可以先求解集，再由子集的含义求解参数的值(或范围)．(2)转化为函数值域问题，即已知函数f(x)的值域为[m，n]，则f(x)≥a恒成立⇒f(x)min≥a，即m≥a；f(x)≤a恒成立

⇒f(x)max≤a，即n≤a.