【文档说明】北京市海淀区北京一零一中2023-2024学年高二下学期期中考试数学试题 Word版.docx，共(4)页，319.223 KB，由小赞的店铺上传

转载请保留链接：https://www.doc5u.com/view-ff9a09f5b03b0cd2d73bf0f2f5ca5fa4.html

以下为本文档部分文字说明：

北京市海淀区北京一零一中2023-2024学年高二下学期期中考试数学试题（本试卷满分120分，考试时间100分钟）命题：高二数学组审稿：贺丽珍一、选择题共10小题，每小题4分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项.1.已知na为等差数列，5

4a=，则46aa+=（）A.4B.6C.8D.102.函数y=12x2−㏑x的单调递减区间为A.（−1,1]B.（0,1]C.[1，+∞）D.（0，+∞）3.由0，1，2，5四个数组成没有重复数字的四位数中，能被5整除的个数是（）A.24B.12C.10

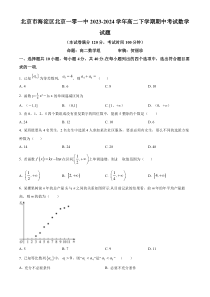
D.64.某班级要从4名男生、2名女生中选派4人参加某次社区服务，要求必须有女生，那么不同的选派方案种数为（）A.14B.24C.28D.485.若函数()lnfxkxx=−在区间1,2+上单调递增，则k取值范围为（）A.1,2+B.)2,+C

.1,4+D.)4,+6.某棵果树前n年的总产量Sn与n之间的关系如图所示.从目前记录的结果看，前m年的年平均产量最高，则m的值为（）A.5B.7C.9D.117.已知等比数列na中，10a，则“14

aa”是“35aa”（）A.充分不必要条件B.必要不充分条件的的C.充要条件D.既不充分也不必要条件8.对于R上可导的任意函数()fx，若当2x时满足()02fxx−，则必有（）A.()()()1322fff+B.()(

)()1322fff+C.()()()1322fff+D.()()()1322fff+9.关于函数2()()2exfxxx=−，下列结论错误的是（）A.()0fx的解集是{|02}xxB.(2)f−是极小值，(2)f是极大值C.()fx没有最小值，也没有最大值D.()fx有最大值，没有

最小值10.数列na的前n项和为nS，若数列na与函数()fx满足：（1）()fx的定义域为R；（2）数列na与函数()fx均单调递增；（3）*nN使()nnSfa=成立，则称数列na与函数()fx具有“单调偶遇关系”.给出下列四

个结论：①21nan=+与()fxx=具有“单调偶遇关系”；②2nna=与()22fxx=−具有“单调偶遇关系”；③与数列{21}n+具有“单调偶遇关系”的函数有有限个；④与数列2n具有“单调偶遇

关系”的函数有无数个.其中所有正确结论的序号为（）A.①③④B.①②③C.②③④D.①②④二、填空题共6小题，每小题5分，共30分.11.在41()xx+的展开式中，常数项为_____．12.函数()(2)exfxx=−的零点个数为__________

__，其极小值为_____________.13.曲线321()2ln2fxxxx=+−在1x=处的切线的方程为__________．14.已知函数()fx的导函数为()fx，能说明“若()0fx对任意的(0,)x+都成立且(

)00f，则()fx在(0,)+上必有零点”为假命题的一个函数是___________.15.“S”型函数是统计分析､生态学､人工智能等领域常见的函数模型，其图象形似英文字母“S”，所以其图象也被称为“S”型曲线.某校生物兴趣小组在0.5毫升培养液中放入5个大草履虫，每隔一段时间统

计一次大草履虫的数量，经过反复试验得到大草履虫的数量y(单位：个)与时间t(单位：小时)的关系近似为一个“S”型函数0.0817437e5ty−=+.已知函数0.08375()174etft−=+0t.的部分

图象如图所示，()ft为()ft的导函数.给出下列四个结论：①对任意13(0,24),(96,144)tt，存2(24,96)t，使得132()()()2ftftft+；②对任意13(0,24),(96,144)tt，存在2(24,96)t，使得31

231()()()ftftfttt−=−；③对任意2(24,96)t，存在13(0,24),(96,144)tt，使得132()()()2ftftft+；④对任意2(24,96)t，存在13(0,24),(96,144)

tt，使得31231()()()=ftftfttt−−.其中所有正确结论的序号是___________.16.已知函数ln(),()exxxfxgxx==，存在12(0,),+Rxx，使得()()12fxgxk==成立.给出下列四个结

论:①当0k时，121xx+;②当0k时，21xkx=;③当0k时，212e2exx+;④当0k时，121xx+.其中所有正确结论的序号是________________.三、解答题共4小

题，共50分.解答应写出文字说明、演算步骤或证明过程.17.已知等差数列na的公差为d，前n项和为nS，满足11a=，0d，且1a，2a，3S成等比数列．（1）求数列na通项公式；（2）记2nannba=+，求数列n

b的前n项和nT．在的18.已知函数3()3fxxx=−．（1）求(0)f的值；（2）求()fx在区间33,2−上最值；（3）若3()()(1)gxfxax=+−，求()gx的单调区间．19.已知函数22()(22)exf

xaxxx=+−+．(1)求曲线()yfx=在点(0,(0))f处的切线方程；(2)若0为函数()fx的极小值点，求a的取值范围；(3)曲线()yfx=是否存在两个不同的点关于y轴对称，若存在，请给出这两个点的坐标及此时a的值，若不存在

，请说明理由．20.在无穷数列na中，11a=，对于任意*Nn，都有*Nna，1nnaa+．设*Nm，记使得nam成立的n的最大值为mb．（1）设数列na为1,4,7,10,，写出1b，2b，3b，4b的值；（2）若nb为等差数列，求出所有可能的数列na；（3）设paq

=，12paaaA+++=，求12qbbb+++的值．（用p，q，A表示）的