【文档说明】吉林省汪清县第六中学2019-2020学年高一下学期期中考试数学（文）试题【精准解析】.doc，共(17)页，775.500 KB，由小赞的店铺上传

转载请保留链接：https://www.doc5u.com/view-923e61437dd98a79b21e3ea04190f485.html

以下为本文档部分文字说明：

汪清六中2019-2020学年度第二学期期中考试高一数学(文科)试题一､单项选择1.某工厂质检员每隔10分钟从传送带某一位置取一件产品进行检测，这种抽样方法是（）A.分层抽样B.简单随机抽样C.系统抽样D.以上都不对【答案】C【解析】【分析】根据系统抽样的特点，样本是在总体

个数比较多的情况下，遵循一定的规则，具有相同的间隔，得到的一系列样本.【详解】由题意可知这个抽样是在传送带上每隔10分钟抽取一产品，是一个具有相同间隔的抽样，并且总体的个数比较多，这是一个系统抽样.故选：C【点睛】本题考查

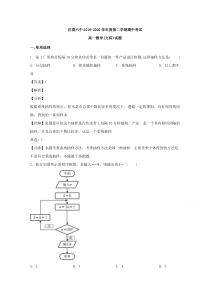
系统抽样方法，考查抽样方法是哪一种抽样，主要考查个体得到的方法是不是符合系统抽样，本题属于基础题.2.执行如图所示的程序框图，若输入8n=，则输出的k=（）A.2B.3C.4D.5【答案】B【解析】由题意得，执行程序框图可知，第一次循环：28117,1nk=+==；第二次循

环：217135,2nk=+==；第三次循环：235171,3nk=+==；第四次循环：2711143n=+=，此时满足判断框的条件，输出k的值，此时3k=，故选B.3.10名工人某天生产同一零件

，生产的件数是15，17，14，10，15，17，17，16，14，12.设其平均数为a，中位数为b，众数为c，则有（）.A.abcB.cbaC.cabD.bca【答案】B【解析】【分析】根据所给数据，分别求出平均数为a，中位数为b，众数为c，然后进行比较

可得选项.【详解】1(15171410151717161412)14.710a=+++++++++=，中位数为1(1515)152b=+=，众数为=17c.故选：B.【点睛】本题主要考查统计量的求解，明确平均数、中位数、众数的求解方法是求解的关键

，侧重考查数学运算的核心素养.4.在0°~360°范围内，与-1050°的角终边相同的角是（）A.30°B.150°C.210°D.330°【答案】A【解析】【分析】由1050336030−=−+可得答案【详解】解：因为1050336030−=−

+所以在0°~360°范围内，与-1050°的角终边相同的角是30°故选：A【点睛】此题考查终边相同角的定义和计算方法，属于基础题.5.袋内分别有红､白､黑球3，2，1个，从中任取2个，则互斥而不对立的两个事件是（）A.至少有一

个白球；都是白球B.至少有一个白球；至少有一个红球C.恰有一个白球；一个白球一个黑球D.至少有一个白球；红､黑球各一个【答案】D【解析】【分析】利用互斥事件、对立事件的定义直接求解【详解】解：对于A，“至少有一个白球”说明有白球，白球的个数可能为1或2，而“都是白球”说明两个

全是白球，这两个事件可以同时发生，故A不是互斥的；对于B，当两球一个白球一个红球时，“至少有一个白球”与“至少有一个红球”均发生，故不互斥；对于C，“恰有一个白球”，表示黑球个数为0或1，这与“一个白球一个黑球”不互斥；对于D，“至少一个白球”

发生时，“红､黑球各一个”不会发生，故互斥，但不对立，故选：D【点睛】此题考查了互斥事件和对立事件，属于基础题.6.某单位有职工160人，其中业务员有104人，管理人员32人，后勤服务人员24人，现用分层抽样法从中抽取一个容量为20的样本，则抽取管

理人员()A.3人B.4人C.7人D.12人【答案】B【解析】【分析】根据分层抽样原理求出应抽取的管理人数．【详解】根据分层抽样原理知，应抽取管理人员的人数为：16010424204160−−=故选：B【点睛】本题考查了分层抽样原理应用问题

，是基础题．7.已知变量x与y正相关，且由观测数据算得样本平均数3x=，3.5y=，则由该观测的数据算得的线性回归方程可能是()A.0.42.3yx=+B.22.4yx=−C.29.5yx=−+D.0.34.4yx=−+【答案】A【解析】试题分析：因为与正相关，排除选项C、D，又因为线性回

归方程恒过样本点的中心，故排除选项B；故选A．考点：线性回归直线.8.某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的产品净重（单位：克）数据绘制的频率分布直方图，其中产品净重的范围是[96，106]，样本数据分组

为[96，98），[98，100),[100，102)，[102，104),[104，106],已知样本中产品净重小于100克的个数是36，则样本中净重大于或等于98克并且小于104克的产品的个数是().A.90B.75C.60D.45【答案】A【

解析】样本中产品净重小于100克的频率为(0.050＋0.100)×2＝0.3，频数为36，∴样本总数为.∵样本中净重大于或等于98克并且小于104克的产品的频率为(0.100＋0.150＋0.125)×2＝0.75，∴样本中净重大于或等于98克并且小

于104克的产品的个数为120×0.75＝90.考点：频率分布直方图.9.有五条线段长度分别为1,3,5,7,9，从这5条线段中任取3条，则所取3条线段能构成一三角形的概率A.110B.310C.12D.710【答案】B【解析】【详解】从五条线段中任取三条共有种可能，其

中能构成三角形的有，，三种可能，故所取三条线段能构成一个三角形的概率为,故选B由题意知本题是一个古典概型.10.下列结论中正确的是()A.小于90°的角是锐角B.第二象限的角是钝角C.相等的角终边一定相同D.终边相同的角一定相等【答案】C【解析】【分析】结合任意角的相关概念逐个进行判定.【详解】对

于A，小于90可能是负角，不是锐角；对于B，第二象限的角可能是负角，不是钝角；对于C，两个角相等，始边一致，则终边一定相同；对于D，终边相同的角，可能相差360°的倍数，不一定相等.故选C.【点睛】本题主要考查任意角的相关

概念，熟知这些概念是求解的关键.11.如果弓形的弧所对的圆心角为3，弓形的弦长为4cm，则弓形的面积是：（）A.2443cm9−B.24c343m−C.28c343m−D.28c323m−【答案】C【解析】【分析】求得弓

形所在圆的半径为r，结合扇形的面积公式和三角形的面积公式，即可求解.【详解】由题意，弓形的弧所对的圆心角为3，弓形的弦长为4cm，可得弓形所在圆的半径为4r=cm，则所在扇形的面积为21184233

S==2cm，234434AOBS==2cm，所以弓形的面积是218(43)3AOBSSScm=−=−.故选：C.【点睛】本题主要考查了扇形的面积公式及其应用，其中解答中熟记扇形的面积公式和三角形的面积公式，准确计算是解答的关键，着重考查运算

与求解能力.12.容量为20的样本数据，分组后的频数如下表：分组)10,20)20,30)30,40)40,50)50,60)60,70频数234542则样本数据落在区间)10,40的频率为（）A.0.35B.0.45C.0.55D.0.65【答案】B【解析】【分析】根据频数表

求出区间)10,40上的频数，可计算出频率．【详解】由已知区间)10,40上的频数为2349++=，∴频率为90.4520=．故选：B．【点睛】本题考查频数分布表，考查频率的概念，属于简单题．二､填空题13.如图是2019年某校举行的元旦诗歌朗诵比赛中，七位评委为某位

选手打出的分数的茎叶统计图，去掉一个最高分和一个最低分，所剩数据的平均数和方差分别为______________【答案】85，1.6【解析】【分析】根据平均数和方差的计算公式直接求解【详解】解：根据题意可得，选手的最后得分为84，84，86，84，87，所以所得分的平均数为1

(8484868487)855++++=，方差为222221[(8485)(8485)(8685)(8485)(8785)]1.65−+−+−+−+−=故答案为：85，1.6【点睛】此题考查了平均数和方差的计算，熟练掌握平均数与方差的计算公式是解决此题的关键，属于基础题.14.

与1991°终边相同的最小正角是______【答案】191【解析】【分析】由19915360191=+直接得答案【详解】解：因为19915360191=+所以与1991°终边相同的最小正角为191故答案为：191【点睛】此题考查了终边相同角的定义和表示方法，属于基础

题.15.半径为cm，中心角为120的扇形的弧长为____________．【答案】223【解析】半径为cm，中心角为120的扇形的弧长为22233=.故答案为223.16.随意地抛一粒豆子，恰好落在图中的方格中(每个方格除颜外完全一样)，那么这粒豆子

停在黑色方格中的概率是_______【答案】13【解析】【分析】假设每个小方格面积为1，求出整个矩形的面积，现同黑色方格的面积，由概率公式可计算出概率．【详解】假设每个小方格面积为1，总共有12个小方格，面积为12，而黑色方格有4个，面

积和为4，因此所求概率为41123P==．故答案为：13．【点睛】本题考查几何概型，掌握面积型几何概型概率公式即可，属于简单题．三､解答题17.已知角2025=.（1）将角改写成2k+(kZ，02)的形式，并指出角是第几象限的角；（2）在区间)5,0−上找出与角

终边相同的角.【答案】（1）5104=+，是第三象限角；（2）19113,,444−−−．【解析】【分析】（1）先把度数改写弧度，再改写成2k+形式，并确定所在象限；（2）解不等式520k−+可得结论．【详解】（1）20

25==45520251018044==+，54是第三象限角，∴是第三象限角．（2）由55204k−+得25588k−−，因为kZ，∴3,2,1k=−−−，对应角依次为19113

,,444−−−．【点睛】本题考查终边相同的角，解题关键是把解写出2,kkZ+或360k+，kZ形式，考查角度与弧度的互化．属于基础题．18.某校举行汉字听写比赛，为了了解本次比赛成绩情况，从得分不低于50分的试卷中随机抽取100名

学生的成绩(得分均为整数，满分100分)进行统计，请根据频率分布表中所提供的数据，解答下列问题：组号分组频数频率第1组[50，60)50.05第2组[60，70)a0.35第3组[70，80)30b第4组[80，90)200.20第5组[90，1

00]100.10合计1001.00（Ⅰ）求ab、的值；（Ⅱ）若从成绩较好的第3、4、5组中按分层抽样的方法抽取6人参加市汉字听写比赛，并从中选出2人做种子选手，求2人中至少有1人是第4组的概率．【答案】(1)35，0.30;(2)35.【解析】试题

分析：（Ⅰ）直接利用频率和等于1求出b，用样本容量乘以频率求a的值；（Ⅱ）由分层抽样方法求出所抽取的6人中第三、第四、第五组的学生数，利用列举法写出从中任意抽取2人的所有方法种数，查出2人至少1人来自第四组的事件个数，

然后利用古典概型的概率计算公式求解．试题解析：（Ⅰ）a＝100－5－30－20－10＝35，b＝1－0.05－0.35－0.20－0.10＝0.30（Ⅱ）因为第3、4、5组共有60名学生，所以利用分层抽样在60名学生中抽取6名学生，每组分别为，第3组：660×

30＝3人，第4组：660×20＝2人，第5组：660×10＝1人，所以第3、4、5组应分别抽取3人、2人、1人设第3组的3位同学为A1、A2、A3，第4组的2位同学为B1、B2，第5组的1位同学为C1，则从6位同学中抽2位同学有15种可能，如下：(A1，A2)，(A1，A

3)，(A1，B1)，(A1，B2)，(A1，C1)，(A2，A3)，(A2，B1)，(A2，B2)，(A2，C1)，(A3，B1)，(A3，B2)，(A3，C1)，(B1，B2)，(B1，C1)，(B2

，C1)．其中第4组被入选的有9种，所以其中第4组的2位同学至少有1位同学入选的概率为915＝35点睛：古典概型中基本事件数的探求方法(1)列举法.(2)树状图法：适合于较为复杂的问题中的基本事件的探求.对于

基本事件有“有序”与“无序”区别的题目，常采用树状图法.(3)列表法：适用于多元素基本事件的求解问题，通过列表把复杂的题目简单化、抽象的题目具体化.(4)排列组合法：适用于限制条件较多且元素数目较多的题目.19.某教研部门对本地区,,ABC三所学校高三年级进行教学质量抽样调查，,

,ABC三所学校高三年级班级数量（单位：个）如下表所示，研究人员用分层抽样的方法从这三所学校中共抽取7个班级进行调查.学校ABC数量（个）211414（Ⅰ）求这7个班级中来自,,ABC三所学校的数量；（Ⅱ）若在

这7个班级中随机抽取2个班级做进一步调查.（i）列出所有可能的结果；（ii）求这2个班级至少有一个来自A学校的概率.【答案】（Ⅰ）这7个班级中来自,,ABC三所学校的数量分别为;（Ⅱ）（i）见解析；（ii）57【解析】【分析】

（Ⅰ）先求出样本容量与总体的个数比，然后确定7个班级中来自,,ABC三所学校的数量；（Ⅱ）设来自A学校的班级分别为：123,,AAA；来自B学校的班级分别为：12,BB;来自C学校的班级分别为：12,CC.（i）用列举法写出所有可能的结果；（ii）通过（i）可以知道这2个班级至少有一个来

自A学校共有15种可能结果，运用古典概型公式，求出这2个班级至少有一个来自A学校的概率.【详解】（Ⅰ）样本容量与总体的个数比为：712114147=++，7个班级中来自,,ABC三所学校的数量分别为：111213,14

2,142777===，所以这7个班级中来自,,ABC三所学校的数量分别为3,2,2;（Ⅱ）设来自A学校的班级分别为：123,,AAA；来自B学校的班级分别为：12,BB;来自C学校的班级分别为：12,CC.（i）这

7个班级中随机抽取2个班级做进一步调查,可能的结果如下：1213111212122321222122313231321211122122

12,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,AAAAABABACACAAABABACACABABACACBBBCBCBCBCCC共有21种可能结果；（ii）由（i）可知这2个班级至少有一个来自A学校共有15种可能结果，

故这2个班级至少有一个来自A学校的概率为155217=.【点睛】本题考查了概率的求法，考查列举法、古典概型基础知识，考查了运算能力.20.高三抽出50名学生参加数学竞赛，由成绩得到如下的频率分布直方图.由于一些数据丢失，试利用频率分

布直方图求：（1）这50名学生成绩的众数与中位数.（2）这50名学生的平均成绩【答案】（1）众数是75，中位数约是76.67；（2）平均成绩是76.5.【解析】【分析】（1）根据众数定义可得众数，中位数要根据频率

计算，求出平分所有小矩形面积的那一点对应的值即可；（2）以每组数据中间值作为估计值，结合频率可计算均值．【详解】（1）从频率分布表知成绩在区间[70,80]上的人数最多，故众数为75，成绩在区间[40,

70]上频率为(0.0040.0060.02)100.3++=，在区间70,80上的频率为0.03100.3=，因此中位数在7080之间，设中位数是x，则700.50.3800.50.4xx−−=−−，解得207076.673x

=+．（2）平均成绩为450.04550.06650.2750.3850.21950.19+++++76.5=．【点睛】本题考查频率分布直方图，由频率分布直方图求众数，中位数，均值，属于

基础题．21.把下列各角的弧度数化为度数，度数化为弧度数.（1）712；（2）136−；（3）1125°；（4）-225°.【答案】（1）105；（2）390−；（3）254；（4）54−.【解析】

【分析】根据弧度制与角度制的互化公式，逐项计算，即可求解.【详解】根据弧度制与角度制的互化公式，1801,1180radrad==，可得：（1）771801051212==；（2）131366180390

==−−−；（3）25112511251804==rad；（4）52252251804−=−=−rad.【点睛】本题主要考查了弧度制与角度制的互化，其中解答中熟记弧度制与角度制的互化公式是解答的关键，着重考查运算与求解能力.22.某高中有高一新生500名，分成水平相同的A，B两类

进行教学实验.为对比教学效果，现用分层抽样的方法从A､B两类学生中分别抽取了40人､60人进行测试.（1）求该学校高一新生A､B两类学生各多少人？（2）经过测试，得到以下三个数据图表：图一：75分以上A､B两类参加测试学生成绩的茎叶图A类B类7，6，5，575，6，7，7，

8，93，181，3，4(茎､叶分别是十位和个位上的数字)(如图)表一：100名测试学生成绩频率分布表：组号分组频数频率1)55,6050.052)60,65200.203)65,704)70,75350.355)

75,806)80,85合计1001.00图二：100名测试学生成绩的频率分布直方图：先填写频率分布表(表一)中的六个空格，然后将频率分布直方图(图二)补充完整；【答案】（1）A类学生200人，B类学生300人.（2）答案见解析.【解析】【分析】（1）根据分层抽样计算各类学生的人数

.（2）根据茎叶图填写频率分布表，由此补全频率分布直方图.【详解】（1）依题意用分层抽样的方法从A､B两类学生中分别抽取了40人､60人.所以A类学生为405002004060=+，B类学生为605003004060=+.（2）根据茎叶图可知，)75,80有10人

，)80,85有5人，由此补全频率分布表如下图所示：组号分组频数频率1)55,6050.052)60,65200.203)65,70250.254)70,75350.355)75,80100

.16)80,8550.05合计1001.00补全频率分布直方图如下图所示：【点睛】本小题主要考查分层抽样，考查茎叶图，频率分布直方图，考查数据处理能力，属于中档题.