【文档说明】2024届高考一轮复习数学试题（新教材人教A版 ）第三章　3.2　导数与函数的单调性 Word版.docx，共(3)页，211.816 KB，由小赞的店铺上传

转载请保留链接：https://www.doc5u.com/view-7c38ebfe3b5d07995ef577e2720ea3b1.html

以下为本文档部分文字说明：

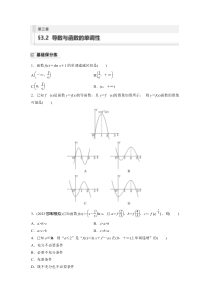
1．函数f(x)＝xlnx＋1的单调递减区间是()A.－∞，1eB.1e，＋∞C.0，1eD．(e，＋∞)2．已知f′(x)是函数y＝f(x)的导函数，且y＝f′(x)的图象如图所示，则y＝f(x)函

数的图象可能是()3．(2023·邯郸模拟)已知函数f(x)＝x－1xlnx，且a＝f23，b＝f45，c＝12(e)f−，则()A．a>b>cB．c>a>bC．a>c>bD．c>b>a

4．已知a∈R，则“a≤2”是“f(x)＝lnx＋x2－ax在(0，＋∞)上单调递增”的()A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件5．(多选)(2023·深圳模拟)若0<x1<x2<1，则()

A．2ex－1ex>lnx2＋1x1＋1B．2ex－1ex<lnx2＋1x1＋1C．x21ex>x12exD．x21ex<x12ex6．(多选)如果函数f(x)对定义域内的任意两实数x1，x2(x1≠x2)都有x1f(x1)－x2f(x2)x1－x2>0，则称函数y＝f(x)为“F函数

”．下列函数不是“F函数”的是()A．f(x)＝exB．f(x)＝x2C．f(x)＝lnxD．f(x)＝sinx7．函数f(x)＝e－xcosx(x∈(0，π))的单调递增区间为________．8．已知函数f(x)＝3xa－2x2＋lnx(a>0)，若函数f(x)在[1,2

]上不单调，则实数a的取值范围是________．9．已知函数f(x)＝aex－x，a∈R.(1)当a＝1时，求曲线y＝f(x)在点(1，f(1))处的切线方程；(2)试讨论函数f(x)的单调性．10．已知a∈R，函数f(x)＝(－x2＋ax)e

x，x∈R.(1)当a＝2时，求函数f(x)的单调递增区间；(2)若函数f(x)在(－1,1)上单调递增，求实数a的取值范围．11．(多选)已知函数f(x)＝ln(e2x＋1)－x，则下列说法正确的是()A．f(ln2)＝ln52B．f(x)是奇函数C．f

(x)在(0，＋∞)上单调递增D．f(x)的最小值为ln212．已知函数f(x)＝ex－e－x＋12sinπ2x＋1，实数a，b满足不等式f(3a＋b)＋f(a－1)<2，则下列不等式成立的是()A．2a＋b<－1B．2a＋

b>－1C．4a＋b<1D．4a＋b>113．(多选)(2023·杭州模拟)已知f(x)＝(a2－1)ex－1－12x2，若不等式f1lnx>f1x－1在(1，＋∞)上恒成立，则a的值可以为()A．－2B．－1C．1D.214．(2023·蚌埠模拟)若x1·12x＝x2

·log2x2＝2024，则x1x2的值为________．