【文档说明】（强化训练）2022-2023学年高三年级新高考数学一轮复习专题-函数的图象 含解析【高考】.docx，共(5)页，92.437 KB，由管理员店铺上传

转载请保留链接：https://www.doc5u.com/view-6796a67bf81a91b9a92e5b89f7fa9841.html

以下为本文档部分文字说明：

1函数的图象学校:___________姓名：___________班级：___________考号：___________一、单选题（本大题共5小题，共25.0分。在每小题列出的选项中，选出符合题目的一项）1.著名数学家华罗庚先生曾说过：

“数缺形时少直观，形缺数时难入微，数形结合百般好，隔裂分家万事休．”在数学的学习和研究中，我们经常用函数的图象来研究函数的性质，也经常用函数的解析式来琢磨函数的图象的特征，如某体育品牌的𝐿𝑂𝐺𝑂为，可抽象为如图所示的轴对称的优美曲线，下列函数中，其图象大致可“完美”局部表达这条曲

线的函数是()A.𝑓(𝑥)=𝑠𝑖𝑛5𝑥2−𝑥−2𝑥B.𝑓(𝑥)=𝑐𝑜𝑠𝑥2𝑥−2−𝑥C.𝑓(𝑥)=𝑐𝑜𝑠5𝑥|2𝑥−2−𝑥|D.𝑓(𝑥)=𝑠𝑖𝑛5𝑥|2𝑥−2−𝑥|2.已知函数𝑓

(𝑥)=14𝑥2+𝑐𝑜𝑠𝑥，𝑓′(𝑥)是函数𝑓(𝑥)的导函数，则𝑓′(𝑥)的图象大致是()A.B.C.D.3.已知函数𝑓(𝑥)=3𝑥+𝑥,𝑔(𝑥)=log3𝑥+𝑥,ℎ(𝑥)=𝑥3+𝑥的零点分别为𝑎,𝑏,𝑐，则𝑎,𝑏,𝑐的大小顺序关系是()A

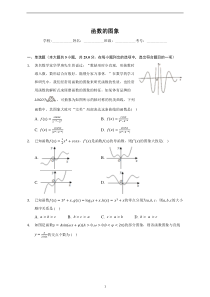
.𝑎>𝑏>𝑐B.𝑏>𝑐>𝑎C.𝑐>𝑎>𝑏D.𝑏>𝑎>𝑐4.如图是函数𝑦=𝐴sin(𝜔𝑥+𝜑)(𝐴>0,𝜔>0,0<𝜑<2𝜋)的部分图象，则该函数图象与直线𝑦=𝑥2021的交点个数为()2A.8083B

.8084C.8085D.80865.已知函数𝑓(𝑥)={𝑥ln𝑥−𝑥,𝑥>0𝑓(𝑥+1),𝑥⩽0，若关于𝑥的方程2𝑓(𝑥)−𝑘𝑥+1=0有四个不同的实根，则实数𝑘的取值范围是()A.

(−14,−16]∪(14,12]B.[−14,−16)∪[14,12)C.(−12,−13]∪(12,1]D.[−12,−13]二、多选题（本大题共4小题，共20.0分。在每小题有多项符合题目要求）6.已知函数𝑓(𝑥)=𝑎𝑥3+𝑏

𝑥+𝑐(𝑎𝑐<0)，则函数𝑦=𝑓(𝑥)的图像不可能是()A.B.C.D.7.已知函数𝑓(𝑥)={|ln𝑥|,𝑥>0,𝑥+1,𝑥⩽0,若方程𝑓(𝑓(𝑥))+𝑎=0有6个不等实根，则实数𝑎的可能取值

是()A.−12B.0C.−1D.−138.已知函数𝑓(𝑥)={𝑥+1,𝑥<0,−𝑥2+2𝑥,𝑥≥0,令𝑔(𝑥)=𝑓(𝑓(𝑥))，则下列说法正确的是()A.𝑔(−1)=0B.方程𝑔(𝑥)=2有3个根C.方程𝑔(𝑥)=−2的所有根之和为−1D.当𝑥<0时，

𝑓(𝑥)≤𝑔(𝑥)9.已知函数𝑓(𝑥)=𝑥|𝑥−𝑎|，其中𝑎∈𝑅，下列结论正确的是A.存在实数𝑎，使得函数𝑓(𝑥)为奇函数B.存在实数𝑎，使得函数𝑓(𝑥)为偶函数3C.当𝑎<0时，若方程𝑓(𝑥)−1=0有三个实根，则𝑎≤−2D.当𝑎>0时，

若方程𝑓(𝑥)=𝑘(𝑥+1)(𝑘>0)有两个实根，则𝑎=𝑘±2√𝑘三、填空题（本大题共6小题，共30.0分）10.若曲线|𝑦|=2𝑥+1与直线𝑦=𝑏没有公共点，则𝑏的取值范围是．11.已知𝑓(𝑥)={𝑥2+𝑥,𝑥≥0,−𝑥2+𝑥,𝑥<0

，则不等式𝑓(𝑓(𝑥))<6的解集为．12.若函数𝑓(𝑥)={|𝑥2+2𝑥−1|,𝑥≤02𝑥−1+𝑎,𝑥>0有两个不同的零点，则实数𝑎的取值范围为．13.已知函数𝑓(𝑥)={ln𝑥,𝑥>02𝑥+1,𝑥⩽0若方程𝑓(𝑥)=𝑎𝑥有三个不同的实数根，则𝑎的

取值范围是．14.已知𝜆∈𝑅，函数𝑓(𝑥)={𝑥−4,𝑥⩾𝜆𝑥2−4𝑥+3,𝑥<𝜆，当𝜆=2时，不等式𝑓(𝑥)<0的解集是.若函数𝑓(𝑥)恰有2个零点，则𝜆的取值范围是．15.已知函数𝑓(𝑥)={

12(|𝑥+3|+1),𝑥⩽0ln𝑥,𝑥>0若存在实数𝑎<𝑏<𝑐，满足𝑓(𝑎)=𝑓(𝑏)=𝑓(𝑐)，则𝑎𝑓(𝑎)+𝑏𝑓(𝑏)+𝑐𝑓(𝑐)的最大值是．四、解答题（本大题共1小题，共12.0分。解答应写出文字说明，证明过程或演算步骤）16.(本

小题12.0分)作出下列函数的图象．(1)𝑦=2−𝑥𝑥+1．(2)𝑦=(12)|𝑥+1|．(3)𝑦=|log2𝑥−1|．(4)𝑦=𝑥2−2|𝑥|−1．41.【答案】𝐶2.【答案】𝐴3.

【答案】𝐵4.【答案】𝐶5.【答案】𝐶6.【答案】𝐴𝐶𝐷7.【答案】𝐴𝐷8.【答案】𝐴𝐶𝐷9.【答案】𝐴𝐷10.【答案】[−1,1]11.【答案】(−∞,1)12.【答案】(−

∞,−12)13.【答案】(0,1𝑒)14.【答案】{𝑥|1<𝑥<4}(1,3]∪(4，+∞)15.【答案】2𝑒2−1216.【答案】解：(1)易知函数的定义域为{𝑥∈𝑅|𝑥≠−1}，𝑦=2−𝑥𝑥+1=−1+3𝑥+1，因此由𝑦=3𝑥的图象向左平移1个单位

长度，再向下平移1个单位长度即可得到函数𝑦=2−𝑥𝑥+1的图象，如图(1)所示；，(2)先作出𝑦=(12)𝑥，𝑥∈[0,+∞)的图象，然后作其关于𝑦轴的对称图象𝑦=(12)|𝑥|，再将整个图象

向左平移1个单位长度，即得到𝑦=(12)|𝑥+1|的图象，如图(2)所示；5(3)先作出𝑦=𝑙𝑜𝑔2𝑥的图象，再将图象向下平移1个单位长度，保留𝑥轴上方的部分，将𝑥轴下方的图象翻折到𝑥轴上方来，即得到𝑦=|

𝑙𝑜𝑔2𝑥−1|的图象，如图(3)所示；(4)𝑦={𝑥2−2𝑥−1(𝑥⩾0),𝑥2+2𝑥−1(𝑥<0)图象如图．