 DOC
DOC
【文档说明】四川省成都市第十二中学(川大附中)2022-2023学年高三下学期三诊热身考试数学理科试题 含解析.docx,共(27)页,1.869 MB,由管理员店铺上传
转载请保留链接:https://www.doc5u.com/view-492761585e10c8f6772b50398a24c176.html
以下为本文档部分文字说明:
川大附中2022—2023学年下期高三三诊热身考试高三数学理科一、单选题(本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,选出符合题目的一项)1.已知集合2230,AxxxBN=−−=∣,则集合AB=
()A.{0}B.{0,1}C.{0,1,2}D.{1,2,3}【答案】C【解析】【分析】先解出集合A再求AB.【详解】由2230|13,AxxxxxBN=−−=−=∣得,{0,1,2}AB=.故选:C【点睛】集合的交、并、补
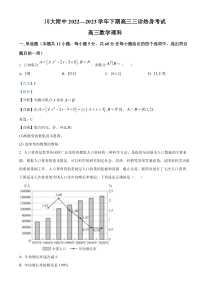
运算:(1)离散型的数集用韦恩图;(2)连续型的数集用数轴.2.人口普查是世界各国所广泛采用的搜集人口资料的一种科学方法,是提供全国基本人口数据的主要来源.根据人口普查的基本情况,可以科学的研究制定社会、经济、科教等各项发展政策,是国家科学决
策的重要基础工作,人口普查资料是制定人口政策的依据和前提.截止目前,我国共进行了七次人口普查,下图是这七次普查的全国人口及年均增长率情况,下列说法正确的是()A.年均增长率逐次减小B.年均增长率的极差是1.08%C.这七次普
查的人口数逐次增加,且第四次增幅最小D.第七次普查的人口数最多,且第三次增幅最大【答案】D【解析】【分析】增幅其实就是增长率,不是增长量。增长率为正的时候,总人口都是增加的;增长率为负的时候,总人口才减少。看图,排除错误选项即可.【详解】对于A选项,由图可知第
三次增幅最大,之后增幅减小,所以年增长率是先增后减的,故A错;对于B选项,极差为2.09%0.53%1.56%−=,故B错;对于C选项,第七次增幅最小,故C错;对于D选项,第七次普查的人口数最多,且第三次增幅最大,故正确故选:D3.已知平面,,直线m,n满足m,n,
则“//mn”是“//”()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】D【解析】【分析】利用平面与平面的位置关系判断充分条件和平面平面平行的性质定理判断必要条件.【详解
】m,n,若//mn,则//或相交,故不充分;若//,由面面平行的性质定理得mn,平行或异面,故不必要;故选:D【点睛】本题主要考查以直线、平面的位置关系为载体的逻辑条件判断,属于基础
题.4.已知函数()fx的图象如图所示,则函数()()gxfx=−的图象为()的A.B.C.D.【答案】B【解析】【分析】根据函数的奇偶性及0x−判断函数正负即可得解.【详解】因为()()gxgx−=,所以()gx为偶函数,其图象关于y轴对称,排除C与D.
又0x−,所以()()0gxfx=−:故选:B.5.下列关于统计概率知识的判断,正确的是()A.将总体划分为2层,通过分层随机抽样,得到两层的样本平均数和样本方差分别为1x,2x和21s,22s,且已知12xx=,则总体方差222121
()2sss=+B.在研究成对数据的相关关系时,相关关系越强,相关系数r越接近于1C.已知随机变量X服从正态分布2(,)N,若()()151PXPX−+=,则2=D.回归直线ˆˆˆybxa=+恒过样本点的中心
(),xy,且至少过一个样本点【答案】C【解析】【分析】A选项,根据均值和方差的定义,通过两层的均值和方差表示出总体的均值和方差,然后进行判断;B选项,根据相关系数的定义进行判断;C选项,根据正态曲线的性质进行判断;D选项,根据回归直线
的性质进行判断.【详解】解:对于A,设2层数据分别记为1212,,,;,,,mnxxxxxx,因为12xx=,所以总体样本平均数为121112mxnxmxnxxxxmnmn++====++,所以()()()()222222112211111111,mmnniijjiij
jsxxxxsxxxxmmnn=====−=−=−=−,所以总体方差()()222111mnijijsxxxxmn===−+−+()22121msnsmn=++2212mnssmnmn=+++,只有当mn=时,()22
21212sss=+才成立,A错误;对于B,相关性越强,r越接近于1,B错误;对于C,若()()151PXPX−+=,则()()511(5),22PXPX+−−===,C正确;对于D,回归直线ˆˆˆ
ybxa=+恒过样本点的中心(),xy,可以不过任一个样本点,D错误.故选:C6.设等比数列na中,37,aa使函数()3223733fxxaxaxa=+++在=1x−时取得极值0,则5a的值是()A.3或32B.3或32C.32D.32【答案】D【解析】【分析】由
极值点和极值可构造方程组求得37,aa,代回验证可知3729aa==满足题意;结合等比数列性质可求得结果.详解】由题意知:()23736fxxaxa=++,()fx在=1x−处取得极值0,()
()23733711301360faaafaa−=−+−+=−=−+=,解得:3713aa==或3729aa==;当31a=,73a=时,()()22363310fxxxx=++=+,()fx\在
R上单调递增,不合题意;当32a=,79a=时,()()()23129313fxxxxx=++=++,当()(),31,x−−−+时,()0fx¢>;当()3,1x−−时,()0fx;()fx\在()(),3,1,−
−−+上单调递增,在()3,1−−上单调递减,1x=−是()fx的极小值点,满足题意;253718aaa==,又5a与37,aa同号,532a=.故选:D.7.欧拉公式iecosisinxxx=+(其中i为虚数单位,xR)是由瑞士
著名数学家欧拉创立的,该公式将指数函数的定义域扩大到复数,建立了三角函数与指数函数的关联,在复变函数论里面占有非常重要的地位.依据欧拉公式,下列选项正确的是()A.πie为虚数B.函数i()exfx=不是周期函数C.若i13ie
2x−=,则2π3x=D.ππii34ee的共轭复数是2626i44−+−【答案】D【解析】【【分析】A选项,根据题意计算出iπe1=−,A错误;B选项,由sin,cosxx是周期函数,得到答案;C选项,根据欧拉公式得到13cos,sin22xx==−,C错误;D选项,计算出ππii34i2ee
66244−+=+,得到共轭复数.【详解】A选项,πiecosπisinπ1+=−=,为实数,A错误;B选项,i()ecosisinxfxxx==+,由于sin,cosxx是最小正周期为2π的函数,所以i()ecosisinxfxxx==+是周期函数,B错误;C选项,由题意得13icosisi
n2xx−+=,所以13cos,sin22xx==−,又2π3x=时,13cos,sin22xx=−=,故C错误;D选项,ππii34ππππeecosisincosisin2213332i42422i
==++++4i26624−+=+,故共轭复数是2626i44−+−,D正确.故选:D8.如图,已知三棱锥−PABC的侧棱长均为2,35APBBPC==,50APC
=,点D在线段PA上,点E在线段PC上,则BDE△周长的最小值为()A.43B.4C.23D.6【答案】A【解析】【分析】作三棱锥−PABC的侧面展开图,结合两点之间线段最短的结论及余弦定理可求BDE△的最小值.
【详解】如图,将三棱锥的侧面展开,则BDE△周长的最小值与展开图中的线段12BB相等.在12PBB△中,12122,353550120PBPBBPB===++=,在12PBB△中,根据余弦定理可得:2221212122cos
120BBPBPBPBPB=+−22122222122=+−−=,所以1223BB=,即BDE△周长的最小值为23.故选:A.9.已知函数()()sinfxAx=+(0A,0,0π)的部分图象如图所示.若π6625f
+=,则22sincos22−的值为()A.35B.45C.35-D.45−【答案】C【解析】【分析】根据题意,结合图像性质求出解析式,再根据诱导公式与二倍角公式,即可求解.【详解】根据题意,结合图像易知,2A=,254312T=−=,
因此22T==,因为函数图像过点2,23−,所以242sin233f=+=−,即4232k+=−+,Zk,由0π,解得6=,故()2sin26fxx=+.又因为π6625f+=
,所以62sin2cos365++==,即3cos5=,因此223sincoscos225−=−=−.故选:C.10.设10abc,给出下列四个结论:①11acbc;②ccbaab;③()()11abcc−−
,④()()loglog++baacbc.其中正确结论有()A.1个B.2个C.3个D.4个【答案】B【解析】【分析】直接利用不等式的性质和对数函数以及指数函数的性质的应用对①②③④进行判断.【详解】由题意,10abc,所以对于①,acbc,故11acbc,所以①错误;对于②,取13
,2,2abc===,则=23cba,32=cab,所以ccbaab,故②错误;对于③,因为011c−,且ab,所以()()11abcc−−,故③正确;对于④,1++acbc,所以()()logloglog()+++abbacbbcc,故④正确.故选:
B.11.在四面体ABCD−中,AB,AC,AD两两垂直且3ABACAD===,以C为球心,2为半径的球2O与该四面体每个面的交线的长度和的值为()A.56B.C.43D.32【答案】D【解析】【分析】设球2O与RtACD的边CD、AD分别交于点M、N,与RtABC的边A
B、CB分别交于点H、G,求出球2O与该四面体四个面的交线的长度,即得解.【详解】解:因为四面体ABCD−中,,,ABACAD两两垂直,且3ABACAD===,由题意知RtACD、RtABC等腰直角三角形,且3ABACAD===,以点C为球心,2为半径作一个球2O,设球2O与RtACD的边CD
、AD分别交于点M、N,如图1;与RtABC的边AB、CB分别交于点H、G,如图2;易得3cos2ACN=,则6ACN=,tan16ANAC==,所以∠NCM=∠ACD-∠ACN=4612−=,所以弧MN的长2
126MN==,同理,弧6GH=.在ABD△内,如图3,因为AH=AN=1,∠HAN=2,则122HN==,又如图4,易知弧GM是以顶点C为圆心,2为半径,圆心角为3,则2233GM==,所以球面与该四面体的每个面的交线的长度和为2366232+++=.
故选:D.12.已知函数()2e,02,0xxxfxxxx=−+,若函数22()3[()]()2()gxfxmfxmm=−−R恰有5个零点12345,,,,xxxxx,且12345xxxxx,()()34fxfx=
,则()()()13322fxfxfx++−的取值范围是()为A.31,00,2ee−B.21,00,3ee−C.32e,00,2e3−D.22e,00,3e3−
【答案】B【解析】【分析】将()fx看成整体解出()fxm=或2()3mfx=−,作出()fx的大致图象,将式子化为()()()()()()()()1331341322222fxfxfxfxfxfxfxfx++−=++=+
,然后转化为m的范围进行分类讨论即可判断.【详解】当0x时,()exfxx=,此时,()()1exfxx=+,令()0fx¢>,解得:10x−,令()0fx,解得:1x−,可得()fx在(
),1−−上单调递减且恒负,在()1,0−上单调递增且恒负,且()11ef−=−,当0x时,()()22211fxxxx=−+=−−+,作出()fx的大致图象如图所示,函数22()3[()]()2()gxfxmfxmm=−−R恰有
5个零点12345,,,,xxxxx,等价于方程223[()]()20fxmfxm−−=有5个不同的实数根,解得:()fxm=或()23mfx=−,0m,该方程有5个根,且()()34fxfx=,则342xx+
=,()()()125fxfxfx==,当0m时,()()()1251,0efxfxfxm===−,()()342(0,1)3mfxfx==−,故1,0em−,所以()()()()()()()()13313413
22222fxfxfxfxfxfxfxfx++−=++=+4222,0333emmm=−=−;当0m时,()()()12521,03efxfxfxm===−−,()()34(0,1)fxfxm==,
故30,2em,所以()()()()()()()()1331341322222fxfxfxfxfxfxfxfx++−=++=+42120,33emmm=−+=,综上:()()()13322fxfxfx+
+−的取值范围是:21,00,3ee−.故选:B.【点睛】关键点点睛:本题的关键点是对223()()20fxmfxm−−=的理解,将()fx看成一个t,解出其值,然后通过图象分析,转化为直线12,ytyt==与图象的交点情况.二、填空题(本大题共4小题,共20分
)13.已知向量(),12=OAk,()4,5=OB,(),10=−OCk,且A、B、C三点共线,则k=_______【答案】23−【解析】【分析】先求出,ABBC的坐标,再根据A、B、C三点共线求出k的值.【详解】由题得(4,7)ABOBOAk=
−=−−,(4,5)BCOCOBk=−=−−,因为A、B、C三点共线,所以=ABBC,所以(4)57(4)0kk−+−−=,所以23k=−.故答案为:23−【点睛】本题主要考查向量的坐标运算和共线向量,考查三点共线,意在考查学生对这些知识的理解掌握水平.14.已知实数,xy满足
()2221xy+−=,223xyxy+=+的取值范围是______.【答案】1,2【解析】【分析】设(),axy=,()1,3b=,利用向量夹角坐标运算可求得2cos=,利用圆的切线的求法可求得(
),axy=所在直线倾斜角的范围,从而确定的范围,进而求得的范围.【详解】由圆的方程知:点(),xy在以()0,2为圆心,1为半径的圆上,设(),axy=,()1,3b=,a与b的夹角为,223cos22abxyabxy+===+,
即2cos=;设直线ykx=与圆()2221xy+−=相切,则圆心到直线距离2211dk==+,解得:3k=,结合图象可知:(),axy=所在直线倾斜角为π2π,33,又()1,3b=所在直线倾斜角为π3,π0,3
,1cos,12,则1,2.故答案为:1,2.【点睛】关键点点睛:本题考查直线与圆位置关系综合应用问题,解题关键是能够利用平面向量夹角公式将所求式子转化为两向量夹角余弦值取值范围的求解问题,采用数形结合的方式来进行求解.15.《算法统宗》是中国古代
数学名著,作者是我国明代数学家程大位.在《算法统宗》中诗篇《李白沽酒》里记载:“今携一壶酒,游春郊外走,逢朋加一倍,人店饮斗九”意思是说,李白去郊外春游时,带了一壶酒,遇见朋友,先到酒店里将壶中的酒增加一倍(假定每次加酒不会溢出),再饮
去其中的3升酒.那么根据这个规则,若李白酒壶中原来有酒00(3)aa升,将李白在第(1,)nnnN…家店饮酒后所剩酒量记为na升,则na=__(用0a和n表示).【答案】023(12)nna+−升【解析】【分析】由题干递推列式,找寻规律,并根据规律计算即
可.【详解】解:李白在第(1,)nnnN…家店饮酒后所剩酒量记为na升,则第一家店饮酒后所剩酒量为1023aa=−升,第二家店饮酒后所剩酒量为22100232(23)323(12)aaaa=−=−−=−+升,第三家店饮酒后所剩酒量为323
202323(122)aaa=−=−++升,第四家店饮酒后所剩酒量为4234302323(1222)aaa=−=−+++升,第n家店饮酒后所剩酒量为211000122323(1222)2323(12)12nnnnnnnnaaaaa−−−=−=
−++++=−=+−−升.故答案为:023(12)nna+−升.16.已知双曲线G的方程221169xy−=,其左、右焦点分别是1F,2F,已知点P坐标为()4,2,双曲线G上点()00,Qxy,()000,0xy
满足11211121QFPFFFPFQFFF=,则12FPQFPQSS−=△△______.【答案】8【解析】【分析】设12QFF的内切圆与三边分别相切于,,DEG,利用切线长相等求得内切圆圆心横坐标为a,又的由11211121QF
PFFFPFQFFF=得P在12QFF的平分线上,进而得到P即为内心,应用双曲线的定义求得面积差即可.【详解】如图,设12QFF的内切圆与三边分别相切于,,DEG,可得1122,,QDQGFDFEFEFG===,又由双曲线定义
可得1228QFQFa−==,则()1212122QDDFQGGFDFGFEFEFa+−+=−=−=,又122EFEFc+=,解得1EFac=+,则E点横坐标为a,即内切圆圆心横坐标为a.又11211121QFPFFFPFQFFF=,可得111
21112121coscosQFPFPFQFFPFPFFQFFF=,化简得112coscosPFQPFF=,即112PFQPFF=,即1PF是12QFF的平分线,由于()4,2P,4a=,可得P即为12QFF的内心,且半径r为2,则121211()288
22FPQFPQSSrQFQF−=−==△△.故答案为:8.【点睛】本题关键点在于先利用切线长定理求得12QFF内切圆圆心横坐标为a,再由11211121QFPFFFPFQFFF=得到P在12QFF的平分线上,结合P的横坐标为a进而得到P即为内心,利用双曲线定义及面积公式即可求解.三
、解答题(本大题共7小题,共70分.解答应写出文字说明,证明过程或演算步骤)17.在ABC中,角、、ABC的对边分别为abc、、,且223sinsin302AA+−=.(Ⅰ)求角A的大小;(Ⅱ)若ABC面积为3,且外接圆半径3R=,求ABC的周长.【答案】(1)3A=;(2)32
1+.【解析】【分析】(1)利用三角函数恒等变换的应用化简已知等式可得tan3A=,结合范围0A,可求A的值;(2)由正弦定理可求a,利用余弦定理可得2360cc−−=,解得c的值,可求周长.【详解】(1
)223sinsin302AA+−=1cos23sin302AA−+−=,即sin3cos0AA−=tan3A=又0A3A=(2)2sinaRA=2sinπ23sin33aRA===ABC
面积为31sin32bcA=,所以bc4=2222cosabcbcA=+−229bcbc+−=2()9391221bccb+=+=+=21bc+=321abc++=+【点睛】本题主要考查余弦定理及正弦定理的应用,属于简单题.对余弦定理一定要熟记两种形式:(1)222
2cosabcbcA=+−;(2)222cos2bcaAbc+−=,同时还要熟练掌握运用两种形式的条件.另外,在解与三角形、三角函数有关的问题时,还需要记住30,45,60ooo等特殊角的三角函数值,以便在解题中直接应用.18.2
020年上半年受新冠疫情的影响,国内车市在上半年累计销量相比去年同期有较大下降.国内多地在3月开始陆续发布促进汽车消费的政策,开展汽车下乡活动,这也是继2009年首次汽车下乡之后开启的又一次大规模汽车下乡活动.某销售
商在活动的前2天大力宣传后,从第3天开始连续统计了6天汽车销售量y(单位:辆)如下表:第x天345678销售量y(单位:辆)172019242427(1)从以上6天中随机选取2天,求这2天的销售量均在20辆以上(含20辆)的概率.(2)根据上表
中前4组数据,求y关于x的线性回归方程ˆˆˆybxa=+.(3)用(2)中的结果计算第7、8天所对应的ˆy,再求ˆy与当天实际销售量y的差,若差值的绝对值都不超过1,则认为求得的线性回归方程“可行”,若“可行”则能通过此回归方程预测以后的销售量.请根据题意
进行判断,(2)中的结果是否可行?若可行,请预测第9天的销售量;若不可行,请说明理由.附:回归直线ˆˆˆybxa=+的斜率和截距的最小二乘法估计值分别为:1221ˆˆˆ,niiiniixynxybaybxxnx==−==−−【答案】(1)25;(2)ˆ211yx=+;(3)可行,29
.【解析】【分析】(1)先确定6天中销售量均在20辆以上(含20辆)有4天,再根据组合以及古典概型概率公式求结果;(2)先求均值,再代入公式求ˆˆ,ba,即得结果;(3)根据回归直线方程确定对应的ˆy,再根据定义判断是否“可行”,最后代入9x=得结果.【详解】(1)6天中销售量均在20辆
以上(含20辆)有4天,242662155CPC===(2)3456172019244.5,2044xy++++++====41317420519624370iiixy==+++=4222221345686iix==+
++=237044.52028644ˆ.5b−==−202ˆ4.511a=−=所以ˆ211yx=+(3)由(2)知,7x=时,141125y=+=,25-24=1;8x=时,161127y=+=,27-27=0所以求得的线性回归方程“可行”9x=时,181129y=
+=【点睛】本题考查古典概型概率公式、线性回归方程及其应用,考查基本分析求解能力,属基础题.19.如图所示多面体ABCDEF中,平面ADE⊥平面ABCD,CF⊥平面ABCD,ADEV是正三角形,四边形ABCD是菱形,2AB=,3CF=,.3BAD=(1)求证:EF平面ABCD;(2)
求二面角EAFC−−的正弦值.【答案】(1)证明见解析(2)108【解析】【分析】(1)由面面垂直的性质定理与线面平行的判定定理证明即可;(2)建立空间直角坐标系,用坐标法计算面面角正弦值即可.【小问1详解】证明:取
AD中点N,连接NENC、,因为ADE是正三角形,所以,2sin603ENADEN⊥==,因为平面ADE⊥平面,ABCDEN平面ADE,平面ADE平面ABCDAD=所以EN⊥平面ABCD,又因为CF⊥平面ABCD,所以ENCF∥,又
因为ENCF=,所以四边形ENCF是平行四边形,所以EFNC∥,又因为NC平面,ABCDEF平面ABCD,所以EF平面ABCD.【小问2详解】连接ACBD、交于O,取AF中点M,连接OM,所以OMCF∥,因为CF⊥平面ABCD,所以OM⊥平面
ABCD,因为OAOB、平面ABCD,所以,OMOAOMOB⊥⊥,又因为四边形ABCD是菱形,所以OAOB⊥,所以OAOBOM、、两两垂直,建立如图所示的空间直角坐标系,()()()()()31313,0,0,0,1
,0,3,0,0,0,1,0,,,0,,,3,3,0,32222ABCDNEF−−−−−,()3123,0,3,,,322AFAE=−=−−,设平面AEF的法向量为(),,mxyz
=,2330313022AFmxzAEmxyz=−+==−−+=,令()1,1,33,2,xm==平面AFC的法向量为()0,1,0n=,设二面角EAFC−−的大小为,2333610cos,sin1cos88421mnmn====−=.所以二面角E
AFC−−的正弦值为108.20.已知O为坐标原点,点13,2P在椭圆2222:1(0)xyCabab+=上,椭圆C的左右焦点分别为12,FF,且1223FF=.(1)求椭圆C的标准方程;(2)若点012,,PPP在椭
圆C上,原点O为012PPP的重心,证明:012PPP的面积为定值.【答案】(1)2214xy+=(2)证明见解析【解析】【分析】(1)根据焦距可确定3c=,再根据点13,2P在椭圆上,代入方程解方程组可得答案.(2)设直线12PP的方程为ykxm=+,和椭圆联立,整理
得到根与系数的关系式,继而根据重心性质表示出0P坐标为2282(,)1414kmmkk−++,代入椭圆方程得到参数之间的关系式,从而再表示出三角形的高,根据面积公式表示出012PPP的面积,将参数间的关系式代入化简即可证明.【小问1详解】
由椭圆C的左右焦点分别为12,FF,且1223FF=,可知:3c=,即223ab=+①,将13,2P代入方程2222:1(0)xyCabab+=得:223114ab+=②,①②联立解得224,1ab==,②故椭圆
的标准方程为2214xy+=.【小问2详解】证明:设000111222(,),(,),(,)PxyPxyPxy,当直线12PP斜率不存在时,即12xx=,由原点O为012PPP的重心,可知0120120,033xxxyyy++++==故可得
此时有01,0)Px(-2,该点在椭圆上,则2114x=,不妨取11x=,则有01233(2,0),(1,),(1,)22PPP−−,或01233(2,0),(1,),(1,)22PPP−−,则此时0121333322PPP
S==;当直线12PP斜率存在时,不妨设12PP方程为ykxm=+,则联立2214ykxmxy=++=,整理得:2221+4)8440kxkmxm++−=(,且需满足22222(8)16(14)(1)16(41)0kmkmkm=−+−=+−,则212122284(
1),1414kmmxxxxkk−−+==++,所以121222()214myykxxmk+=+−=+,由原点O为012PPP的重心知,012012(),()xxxyyy=−+=−+,故0P坐标为2282(,)1414kmmkk−++,代入到2214xy+=中,化简得:222282()4()
41414kmmkk−+=++,即22414mk=+,又原点O为012PPP的重心,故0P到直线12PP的距离为原点O到直线12PP距离的3倍,所以23||1mdk=+,而222212122284(1)|1||1()414|14kmmkxxkkkPP−−=+−=+−
++=2222222244144111414kmmmkkkk+−−+=+++=2243||114mkk++,因此012212221143||3||||122141PPPmmSPPdkkk==+++=222263||63||3
3(14)42mmkm==+,综合上述可知:012PPP的面积为定值.【点睛】本题考查了椭圆方程的求法以及重心性质的应用,以及椭圆内的特殊三角形面积问题,运算量比较复杂而且计算量较大,解决本题的关键是设出直线方程,要利用重心性质表示出一个点的坐标并代入椭圆方程中,找到两
参数之间的关系式,然后三角形面积的表示这点并不困难,表示的方法也比较常规,但需要计算时十分细心还要有耐心.21.已知函数()ln1axafxx+−=.(1)求()fx在()()1,1f处的切线方程;(2)(i)若()1xfxx
−恒成立,求a的取值范围;(ii)当1a=时,证明:()()()212323192224ffnnnnf++++−+.【答案】(1)2yxa=+−(2)(i)0,1;(ii)证明见解析【解析】【分析】(1)求出()1f、()1f的值,利用导数的几
何意义可得出所求切线的方程;(2)(i)由题意可得ln0xaxa−−,设()lnhxxaxa=−−,其中0x,对实数a的取值进行分类讨论,利用导数分析函数()hx在()0,+上的单调性,在0a=、0a的情况下
,验证()0hx在()0,+上能否恒成立,在0a时,可得出()min0hx,求出实数a的取值范围,综合即可得解;(ii)当1a=时,()2lnfnnnn=;结合(i)中所求,可得22ln1112nnn−,在2n=时,直接
验证结论即可;在3n时,利用不等式进行适度放缩,结合裂项求和,即可容易证明.【小问1详解】解:因为()ln1axafxx+−=,则()()22ln11lnaxaxaaxxfxxx−+−−==,其中0x,所以,
()11fa=−,()11f=,所以,函数()fx在点()()1,1f处的切线方程为()11yax−−=−,即2yxa=+−.【小问2详解】解:(i)()ln11xfxaxax=+−−,可得ln0xaxa−−.令()lnhxxaxa=−−,其中0x,则()1axahx
xx−=−=.①当0a=时,()0hxx=,合乎题意;②当a<0时,由基本不等式可得()()()()11122aaaaaa+=−−+−−=−−−,当且仅当1a=−时,等号成立,221331244aaa++=++,当且仅当
12a=−时,等号成立,所以,()1112221313eee1e04e4aaaaaahaaaaaa+++−=−+−=−++−=−,所以,()0hx不恒成立,不合乎题意;③当0a时,()1
axahxxx−=−=,当0xa时,()0hx,此时函数()hx单调递减,当xa时,()0hx,此时函数()hx单调递增,所以,()()minlnln0hxhaaaaaaa==−−=−,可得ln0a,解得01a.综上所
述,实数a的取值范围是0,1;(ii)当1a=时,()lnxfxx=,所以()2lnfnnnn=.由(i)知:()1xfxx−,即ln1xx−,所以ln11xxx−.令2xn=,得222ln11nnn−,即222ln11nnn−,所以22ln1112nnn−.当
2n=时,()2ln224f=,则1193222248nn+−=+,显然ln213448,结论成立;当3n时,()()()22222223ln2ln3ln11111112323223fffnnnnn+++=+++−+−++−
()()()222111111111112232434451nnnnn=−−+++−−+++++()1111111112434451nnn=−−+−
+−++−+()171111911912121211222224nnnnnn=−−−=+−=+−+++,结论成立.因此,当2n时,()()()212323192224ffnnnnf++++−+
成立.【点睛】方法点睛:利用导数证明不等式问题,方法如下:(1)直接构造函数法:证明不等式()()fxgx(或()()fxgx)转化为证明()()0fxgx−(或()()0fxgx−),进而构造辅助函数()()()hxfxgx=−;(2)适当放缩构造法:一是根据已知条件适当放缩;二是利用
常见放缩结论;(3)构造“形似”函数,稍作变形再构造,对原不等式同解变形,根据相似结构构造辅助函数.22.在平面直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线1C的极坐标方程为2c
os=,曲线2C的极坐标方程为2253cos2=+.(1)写出曲线2C的参数方程;(2)设A是曲线1C上的动点,B是曲线2C上的动点,求,AB之间距离的最大值.【答案】(1)2cos:2sinxCy==,(为参数).(2)4313+【解析】
【分析】(1)利用极坐标和直角坐标方程的互化公式和二倍角公式可得2C的直角坐标方程为2214yx+=,再根据圆锥曲线参数方程可得2C的参数方程为cos2sinxy==,(为参数);(2)根据题意
可得,AB之间距离的最大值为点B到圆心1C的距离的最大值再加上半径,根据二次函数性质即可求得最大值.【小问1详解】根据曲线2C的极坐标方程为2253cos2=+可得,()2226cos8+=,即22828xy+=,所以曲
线2C的直角坐标方程为2214yx+=;根据圆锥曲线参数方程定义可得,曲线2C的参数方程为cos2sinxy==,(为参数).小问2详解】由曲线1C的极坐标方程为2cos=可得,曲线1C的直角坐标方程为()2211xy−+=,其圆心()1
1,0C,半径1r=;由题意可得设()cos,2sinB,易知,AB之间距离的最大值为点B到圆心1C的距离的最大值再加上半径,即()()2221maxcos12sin13cos2cos51ABBCr=+=−++=−−++,由二次函数性质可知,当1cos3=−时,max4313AB=+
;所以,AB之间距离的最大值为4313+23.已知函数()211fxxx=−++.(1)解不等式()6fx;(2)记函数()()1gxfxx=++的最小值为m,若,,abcR,且230abcm++−=,
求222abc++的最小值.【【答案】(1)22xx−;(2)914.【解析】【分析】(1)利用零点分界法即可求解.(2)利用绝对值三角函数不等式可得3m=,进而可得233abc++=,再利用柯西不等式即可求解.【详解】解:(1)()161216xfxxx−−−−或1
121216xxx−−++或122116xxx−++,解得22x−,即不等式()6fx的解集为22xx−.(2)()()1212221223gxfxxxxxx=++=−++−−−=,当且仅当()()21220xx−+时取等
号,∴3m=.故233abc++=.由柯西不等式()()()2222222123239abcabc++++++=,整理得222914abc++,当且仅当123abc==,即314a=,614b=,914c=时等号
成立.所以222abc++的最小值为914.【点睛】本题考查了分类讨论解不等式、绝对值三角不等式、柯西不等式,属于基础题.获得更多资源请扫码加入享学资源网微信公众号www.xiangxue100.com