【文档说明】2023届高考人教A版数学一轮复习试题（适用于老高考旧教材）课时规范练44　空间几何中的向量方法含解析.docx，共(9)页，216.432 KB，由envi的店铺上传

转载请保留链接：https://www.doc5u.com/view-45ad152f9f1809c148ed48ed26d48d02.html

以下为本文档部分文字说明：

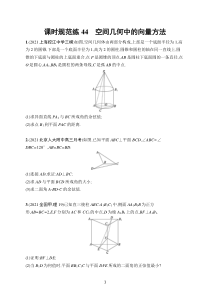
1课时规范练44空间几何中的向量方法1.(2021上海控江中学三模)如图,空间几何体由两部分构成,上部是一个底面半径为1,高为2的圆锥,下部是一个底面半径为1,高为2的圆柱,圆锥和圆柱的轴在同一直线上

,圆锥的下底面与圆柱的上底面重合,点P是圆锥的顶点,AB是圆柱下底面圆的一条直径,点O是圆心,AA1,BB1是圆柱的两条母线,C是弧AB的中点.(1)求异面直线PA1与BC所成角的余弦值;(2)求点B1到平面PAC的距离.2.(2021北京人大附中高三月考)如图,已知平面A

BC⊥平面BCD,∠ABC=∠DBC=120°,AB=BC=BD.(1)连接AD,求证:AD⊥BC;(2)求AD与平面BCD所成角的大小;(3)求二面角A-BD-C的余弦值.3.(2021全国甲,理19)已知直三棱柱ABC-A1B1C1中,侧面AA1B1B为正方形,AB=BC=2,E,F分

别为AC和CC1的中点,D为棱A1B1上的点,BF⊥A1B1.(1)证明:BF⊥DE;(2)当B1D为何值时,平面BB1C1C与平面DFE所成的二面角的正弦值最小?24.(2021湖南常德一模)如图,已知斜三棱柱ABC-A1B1C1的底面是边长为2的正三角形,D为△ABC

所在平面内一点,且四边形ABCD是菱形,AC∩BD=O,四边形ACC1A1为正方形,平面A1DC1⊥平面A1B1C1.(1)求证:B1O⊥平面ABCD;(2)求二面角C-DC1-A1的正弦值.5.(2021湖南长郡中学高三模拟)如图所示的几何体是由等高的半个圆柱

和14个圆柱拼接而成,点G为弧CD的中点,且C,E,D,G四点共面.(1)证明:平面BFD⊥平面BCG;(2)若平面BDF与平面ABG所成锐二面角的余弦值为√155,求直线DF与平面ABF所成角的大小.6.(2021山东日照二模)如图,在三棱锥A-BCD中,∠BCD=90°,BC=C

D=1,∠ACB=∠ACD=θ.(1)求证:AC⊥BD.(2)有三个条件:①θ=60°;②直线AC与平面BCD所成的角为45°;③二面角A-CD-B的余弦值为√33.请你从中选择一个作为条件,求直线BC与平面ACD所成角的正弦值.

3答案：课时规范练1.解:(1)根据题意可得OP⊥平面ABC,∵C是弧AB的中点,∴OC⊥AB,则以O为原点,OC为x轴,OB为y轴,OP为z轴,建立空间直角坐标系,如图.则P(0,0,4),A1(0,

-1,2),B(0,1,0),C(1,0,0),𝑃𝐴1⃗⃗⃗⃗⃗⃗⃗=(0,-1,-2),𝐵𝐶⃗⃗⃗⃗⃗=(1,-1,0),cos<𝑃𝐴1⃗⃗⃗⃗⃗⃗⃗,𝐵𝐶⃗⃗⃗⃗⃗>=𝑃𝐴1⃗⃗⃗⃗⃗⃗⃗⃗·𝐵𝐶⃗⃗⃗⃗⃗|𝑃𝐴1⃗⃗⃗⃗⃗⃗⃗⃗||𝐵𝐶⃗⃗⃗⃗⃗|=1

√5×√2=√1010,∴异面直线PA1与BC所成角的余弦值为√1010.(2)B1(0,1,2),A(0,-1,0),PB1⃗⃗⃗⃗⃗⃗⃗=(0,1,-2),PA⃗⃗⃗⃗⃗=(0,-1,-4),PC⃗⃗⃗⃗=(1,0,-4),设平面PAC的法向量

n=(x,y,z),则{𝑛·𝑃𝐴⃗⃗⃗⃗⃗=-𝑦-4𝑧=0,𝑛·𝑃𝐶⃗⃗⃗⃗⃗=𝑥-4𝑧=0,取z=1,得n=(4,-4,1),∴点B1到平面PAC的距离为d=|𝑃𝐵1⃗⃗⃗⃗⃗⃗⃗⃗·𝑛||𝑛

|=6√33=2√3311.2.(1)证明作AO⊥BC于点O,连接OD,因为平面ABC⊥平面BCD,所以AO⊥平面BCD.因为∠ABC=∠DBC=120°,所以∠ABO=∠DBO.又AB=BD,OB=OB,所以△AOB≌△DOB

,所以∠DOB=90°.又OD⊂平面BCD,所以OA⊥OD,所以OA,OC,OD两两垂直.4分别以OD,OC,OA为x轴,y轴,z轴建立如图所示的空间直角坐标系,设AB=BC=BD=1,则OB=12,OA=OD=√32.则A0,

0,√32,B0,12,0,C0,32,0,D√32,0,0.所以𝐴𝐷⃗⃗⃗⃗⃗=√32,0,-√32,𝐵𝐶⃗⃗⃗⃗⃗=(0,1,0).所以𝐴𝐷⃗⃗⃗⃗⃗·𝐵𝐶⃗⃗⃗⃗⃗=0.所以AD⊥BC.(2)解:由(1)知𝐴𝐷⃗⃗⃗⃗⃗

=√32,0,-√32,平面BCD的一个法向量为n1=(0,0,1).设AD与平面BCD所成的角为α,则sinα=|cos<n1,𝐴𝐷⃗⃗⃗⃗⃗>|=𝑛1·𝐴𝐷⃗⃗⃗⃗⃗⃗|𝑛1||𝐴𝐷⃗⃗⃗⃗⃗⃗

|=-√32√34+34·1=√22.因为0°≤α≤90°,所以AD与平面BCD所成角α=45°.(3)解:设平面ABD的一个法向量为n2=(x,y,z),由𝐴𝐷⃗⃗⃗⃗⃗=√32,0,-√32,𝐴𝐵⃗⃗⃗⃗⃗=0,12,-√32,可得{𝑛2·𝐴𝐷⃗⃗⃗⃗⃗=√3

2𝑥-√32𝑧=0,𝑛2·𝐴𝐵⃗⃗⃗⃗⃗=12𝑦-√32𝑧=0.令x=1,则n2=(1,√3,1).所以cos<n1,n2>=𝑛1·𝑛2|𝑛1||𝑛2|=11·√1+3+1=√55.由题知

二面角A-BD-C为钝角,故其余弦值为-√55.3.证明(1)如图,连接A1E,取BC中点M,连接B1M,EM.5∵E,M分别为AC,BC中点,∴EM∥AB.又AB∥A1B1,∴A1B1∥EM,则点A1,B1,M

,E四点共面,故DE⊂平面A1B1ME.又在侧面BCC1B1中,△FCB≌△MBB1,∴∠FBM=∠MB1B.又∠MB1B+∠B1MB=90°,∴∠FBM+∠B1MB=90°,∴BF⊥MB1.又BF⊥A1B1,MB1∩A1B1=B1,MB1,A1B1⊂平面A1B1ME

,∴BF⊥平面A1B1ME,∴BF⊥DE.(2)∵BF⊥A1B1,∴BF⊥AB,∴AF2=BF2+AB2=CF2+BC2+AB2=9.又AF2=FC2+AC2,∴AC2=8,则AB⊥BC.如图,以B为原点,BC,BA,BB1为x轴,y轴,z轴建立空间直角坐标系,

则B(0,0,0),C(2,0,0),A(0,2,0),E(1,1,0),F(2,0,1).则𝐸𝐹⃗⃗⃗⃗⃗=(1,-1,1),𝐸𝐷⃗⃗⃗⃗⃗=(-1,t-1,2),设DB1=t,则D(0,t,2),0≤t≤2.则平面BB1C1C的法向量为m=(

0,1,0),设平面DEF的法向量为n=(x,y,z),∴{𝐸𝐹⃗⃗⃗⃗⃗·𝑛=0,𝐸𝐷⃗⃗⃗⃗⃗·𝑛=0,即{𝑥-𝑦+𝑧=0,-𝑥+(𝑡-1)𝑦+2𝑧=0,∴n=(1+t,3,2-t).则cos<m,n>=3√(1+𝑡)2+32+(2-𝑡)2=3√2𝑡2-2𝑡

+14.要求最小正弦值,则求最大余弦值.当t=12时二面角的余弦值最大,则B1D=12时二面角正弦值最小.64.(1)证明如图,取A1C1的中点M,连接MD,MB1,MO.由题意可知B1M∥BD,B1M=BO=OD,所以

四边形B1MDO是平行四边形.因为A1B1=B1C1,所以B1M⊥A1C1.因为四边形ACC1A1为正方形,所以OM⊥A1C1.又OM∩B1M=M,所以A1C1⊥平面B1MDO.又MD⊂平面B1MDO

,所以A1C1⊥DM.又平面A1DC1⊥平面A1B1C1,平面A1DC1∩平面A1B1C1=A1C1,DM⊂平面A1DC1,所以DM⊥平面A1B1C1.又平面ABCD∥平面A1B1C1,所以DM⊥平面ABCD.因为四边形

B1MDO是平行四边形,所以B1O∥DM,所以B1O⊥平面ABCD.(2)解:以O为坐标原点,OC,OD,OB1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系如图所示,则C(1,0,0),D(0,√3,0),C1(1,√3,1),A1(-1,√3,1)

,所以𝐶𝐷⃗⃗⃗⃗⃗=(-1,√3,0),𝐷𝐶1⃗⃗⃗⃗⃗⃗⃗=(1,0,1),𝐴1𝐶1⃗⃗⃗⃗⃗⃗⃗⃗⃗=(2,0,0),𝑂𝐷⃗⃗⃗⃗⃗⃗=(0,√3,0).设平面CDC1的法向量为m=(x,y,z),则{𝑚·𝐶𝐷⃗⃗⃗⃗

⃗=0,𝑚·𝐷𝐶1⃗⃗⃗⃗⃗⃗⃗=0,即{-𝑥+√3𝑦=0,𝑥+𝑧=0,令y=1,则x=√3,z=-√3,所以m=(√3,1,-√3)为平面CDC1的一个法向量.因为𝑂𝐷⃗⃗⃗⃗⃗⃗·𝐴1𝐶1⃗⃗⃗⃗⃗⃗⃗⃗⃗=0,𝑂𝐷⃗⃗⃗⃗⃗⃗·𝐷𝐶1⃗⃗⃗⃗⃗⃗⃗=0,所以�

�𝐷⃗⃗⃗⃗⃗⃗=(0,√3,0)为平面A1DC1的一个法向量.设二面角C-DC1-A1的大小为θ,则|cosθ|=|cos<m,𝑂𝐷⃗⃗⃗⃗⃗⃗>|=|𝑚·𝑂𝐷⃗⃗⃗⃗⃗⃗||𝑚||𝑂𝐷⃗⃗⃗⃗⃗⃗|=√3√7×√3=√77,所以sinθ=√1-cos2𝜃=√4

27.所以二面角C-DC1-A1的正弦值为√427.5.(1)证明如图,连接CE,由题意得∠ECD=∠DCG=45°,所以∠ECG=90°,CE⊥CG,因为BC∥EF,BC=EF,所以四边形BCEF为平行四边形,BF∥EC,BF⊥CG,7因为BC⊥平面ABF,BF⊂平面ABF,所以BC⊥BF

,因为BC∩CG=C,所以BF⊥平面BCG,因为BF⊂平面BFD,所以平面BFD⊥平面BCG.(2)解:如图,以A为坐标原点建立空间直角坐标系,设AF=2,AD=t,则A(0,0,0),B(0,2,0),F(2,0,0),D(0,0,t),G(-1,1,t),𝐴

𝐵⃗⃗⃗⃗⃗=(0,2,0),𝐴𝐺⃗⃗⃗⃗⃗=(-1,1,t),𝐹𝐵⃗⃗⃗⃗⃗=(-2,2,0),𝐹𝐷⃗⃗⃗⃗⃗=(-2,0,t),设平面BDF的法向量为n=(x,y,z),则{𝑛·𝐹𝐵⃗⃗⃗⃗⃗=0,𝑛·𝐹𝐷⃗⃗⃗⃗⃗=

0,即{-2𝑥+2𝑦=0,-2𝑥+𝑡𝑧=0,令z=2,则n=(t,t,2),设平面ABG的一个法向量为m=(x',y',z'),则{𝑚·𝐴𝐵⃗⃗⃗⃗⃗=0,𝑚·𝐴𝐺⃗⃗⃗⃗⃗=0,即{𝑦'=0,-𝑥'+𝑦'+𝑡𝑧'=0,令z'=1,则m=(t,0,1)

,因为平面BDF与平面ABG所成锐二面角的余弦值为√155,所以|cos<m,n>|=|𝑚·𝑛||𝑚||𝑛|=𝑡2+2√2𝑡2+4·√𝑡2+1=√155,解得t=2,即AD=2,因为DA⊥平面ABF,所以∠DFA即直线DF与平面ABF所成的角,在△ADF中,因为∠DAF=90

°,AD=AF=2,所以∠DFA=45°,故直线DF与平面ABF所成的角为45°.6.(1)证明如图,取BD的中点O,连接OA,OC,则OC⊥BD.因为BC=DC,∠ACB=∠ACD=θ.AC=AC,所以△ABC≌△ADC,所以AB=AD,所以OA⊥BD.又OA∩

OC=O,所以BD⊥平面AOC.8又AC⊂平面AOC,所以AC⊥BD.(2)解:在直线AC上取点P,使得∠POC=90°,连接PB,PD,由(1)知BD⊥平面AOC,PO⊂平面AOC,所以BD⊥PO.又OC∩BD=O,所以PO⊥平面BCD.由(1)知OC⊥BD,所以OC,OD

,OP两两互相垂直.以O为原点,OC,OD,OP所在直线分别为x轴、y轴、z轴,建立空间直角坐标系.如图所示.因为∠BCD=90°,BC=CD=1,所以OC=OB=OD=√22.又PO⊥平面BCD,所以PB=PC=PD.选①,由θ=60°,可知△PCD是等边三角形,所以PD=CD=1,OP=√22

.所以P(0,0,√22),C√22,0,0,D0,√22,0,B(0,-√22,0),所以𝐵𝐶⃗⃗⃗⃗⃗=(√22,√22,0),𝐷𝐶⃗⃗⃗⃗⃗=√22,-√22,0,𝐷𝑃⃗⃗⃗⃗⃗=(0,-√22,√22).设平面PCD的法向量为n=(x

,y,z),则{𝑛·𝐷𝐶⃗⃗⃗⃗⃗=√22𝑥-√22𝑦=0,𝑛·𝐷𝑃⃗⃗⃗⃗⃗=-√22𝑦+√22𝑧=0,取x=1,则y=z=1,所以n=(1,1,1)为平面PCD的一个法向量.设

直线BC与平面PCD所成的角为α,则sinα=|cos<𝐵𝐶⃗⃗⃗⃗⃗,n>|=|𝐵𝐶⃗⃗⃗⃗⃗·𝑛||𝐵𝐶⃗⃗⃗⃗⃗||𝑛|=√21×√3=√63.因为平面ACD与平面PCD为同一个平面,所以直线BC

与平面ACD所成角的正弦值为√63.选②,由PO⊥平面BCD,可知∠PCO为直线AC与平面BCD所成的角,所以∠PCO=45°,所以OP=OC=√22.所以P(0,0,√22),C(√22,0,0),D(0,√2

2,0),B0,-√22,0,所以𝐵𝐶⃗⃗⃗⃗⃗=(√22,√22,0),𝐷𝐶⃗⃗⃗⃗⃗=(√22,-√22,0),𝐷𝑃⃗⃗⃗⃗⃗=90,-√22,√22.设平面PCD的法向量为n=(x,y,z),则{𝑛·𝐷𝐶⃗⃗⃗⃗⃗=√22𝑥-√22𝑦=0,𝑛·𝐷

𝑃⃗⃗⃗⃗⃗=-√22𝑦+√22𝑧=0,取x=1,则y=z=1,所以n=(1,1,1)为平面PCD的一个法向量.设直线BC与平面PCD所成的角为α,则sinα=|cos<𝐵𝐶⃗⃗⃗⃗⃗,n>|=|𝐵𝐶⃗⃗⃗⃗⃗·𝑛||𝐵𝐶⃗⃗⃗⃗⃗||𝑛|=√21×√3=√63.

因为平面ACD与平面PCD为同一个平面,所以直线BC与平面ACD所成角的正弦值为√63.选③,作PM⊥CD,垂足为M,连接OM.由PO⊥平面BCD,CD⊂平面BCD,可知PO⊥CD.又PO∩PM=P,所以C

D⊥平面POM,所以CD⊥OM,所以∠PMO为二面角A-CD-B的平面角.所以cos∠PMO=√33,所以tan∠PMO=√2.因为OM=√22×√221=12,所以OP=OMtan∠PMO=√22.所以P(0,0,√2

2),C(√22,0,0),D(0,√22,0),B0,-√22,0,所以𝐵𝐶⃗⃗⃗⃗⃗=(√22,√22,0),𝐷𝐶⃗⃗⃗⃗⃗=(√22,-√22,0),𝐷𝑃⃗⃗⃗⃗⃗=(0,-√22,√22).设平面PCD的法向量为n=(x,y,z

),则{𝑛·𝐷𝐶⃗⃗⃗⃗⃗=√22𝑥-√22𝑦=0,𝑛·𝐷𝑃⃗⃗⃗⃗⃗=-√22𝑦+√22𝑧=0,取x=1,则y=z=1,所以n=(1,1,1)为平面PCD的一个法向量.设直线BC与平面PCD所

成的角为α,则sinα=|cos<𝐵𝐶⃗⃗⃗⃗⃗,n>|=|𝐵𝐶⃗⃗⃗⃗⃗·𝑛||𝐵𝐶⃗⃗⃗⃗⃗||𝑛|=√21×√3=√63.因为平面ACD与平面PCD为同一个平面,所以直线BC与平面ACD所成角的正弦值为√63.