【文档说明】西藏拉萨市那曲第二高级中学2019-2020学年高二下学期期末考试数学（理）试卷【精准解析】.doc，共(17)页，1.234 MB，由小赞的店铺上传

转载请保留链接：https://www.doc5u.com/view-d831efc184f1479638f1eaae93e7fe05.html

以下为本文档部分文字说明：

2019—2020学年第二学期期末考试高二数学（理科）试卷（请将所有答案都填入答题卡中，答在试卷纸上无效，共150分，考试时间：120分钟）一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．）1.若(1i)2

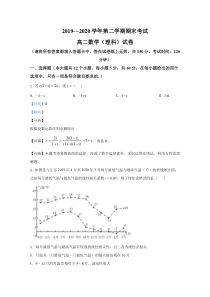
iz+=，则z=（）A.1i−−B.1+i−C.1i−D.1+i【答案】D【解析】【分析】根据复数运算法则求解即可.【详解】()(2i2i1i1i1i1i1i)()z−===+++−．故选D．【点睛】本题考查

复数的商的运算，渗透了数学运算素养．采取运算法则法，利用方程思想解题．2.如图是九江市2019年4月至2020年3月每月最低气温与最高气温（℃）的折线统计图：已知每月最低气温与最高气温的线性相关系数r＝0.83，则下列结论错误的是（）A.每月最

低气温与最高气温有较强的线性相关性，且二者为线性正相关B.月温差（月最高气温﹣月最低气温）的最大值出现在10月C.9﹣12月的月温差相对于5﹣8月，波动性更大D.每月最高气温与最低气温的平均值在前6个月逐月增加【答案】D【解析】【分析】根据相关系

数的性质判断A；根据所给折线图，对B，C，D逐项进行判断.【详解】每月最低气温与最高气温的线性相关系数r＝0.83，比较接近于1，则每月最低气温与最高气温有较强的线性相关性，且二者为线性正相关，则A正确；由所给的折线图

可以看出月温差（月最高气温﹣月最低气温）的最大值出现在10月，则B正确；5﹣8月的月温差分别为18,17,16,16，9﹣12月的月温差分别为20,31,24,21，则9﹣12月的月温差相对于5﹣8月，波动性更大，C正确；每月的最高气温与最低气温的平均值在前5

个月逐月增加，第六个月开始减少，所以A正确，则D错误；故选：D【点睛】本题主要考查了根据折线图解决实际问题以及相关系数的性质的应用，对于相关系数r，r越接近于1，两个变量的线性相关程度越强，属于中档题.3.利用独立性检验的方法

调查高中生性别与爱好某项运动是否有关，通过随机调查200名高中生是否爱好某项运动，利用列联表，由计算可得27.432K，参照下表：()20PKk0.250.150.100.050.0250.0100.0050.00

10k1.3232.0722.7063.8415.0246.6357.87910.828得到的正确结论是（）A.有99%以上的把握认为“爱好该项运动与性别无关”B.有99%以上的把握认为“爱好该项运动与性别有关”C.在犯错误的概率不超过0.5%的前提下，认为“爱好该项运动与性别有关”D.在

犯错误的概率不超过0.5%的前提下，认为“爱好该项运动与性别无关”【答案】B【解析】【分析】根据提供的观测值，把观测值同表格所给的临界值进行比较，看观测值大于哪一个临界值，得到说明两个变量有关系的可信程度.【详解】由27.4326.635K，可得有99%以上的把握认为“爱好该项运动与性

别有关”.故选：B.【点睛】本题考查了独立性检验，即两个变量之间的关系可信程度与临界值表的应用问题，属于基础题.4.函数lnxyx=的单调递减区间是A.1(0,)eB.1(,)e+C.(0,)eD.(,)

e+【答案】D【解析】21ln0,0xyxxex−=所以单调递减区间是(),e+，选D.5.下列有关线性回归分析的四个命题：①线性回归直线必过样本数据的中心点(),xy；②回归直线就是散点图中经过样本数据

点最多的那条直线；③当相关性系数0r时，两个变量正相关；④如果两个变量的相关性越强，则相关性系数r就越接近于1.其中真命题的个数为（）A.1个B.2个C.3个D.4个【答案】B【解析】【分析】根据回归方程及相关概念判断即可.

【详解】①线性回归直线必过样本数据的中心点（,xy）,故①正确;②回归直线在散点图中可能不经过任一样本数据点，故②错误;③当相关性系数0r时,则两个变量正相关，故③正确;④如果两个变量的相关性越强,则相关性系数r就越接近于1或

-1，故④错误.故真命题的个数为2个故选：B【点睛】本题主要考查了线性回归方程，相关系数，样本数据中心点，属于容易题.6.设随机变量()0,1N，若()1Pp=，则()10P−=（）A.12p

+B.1p−C.12p−D.12p−【答案】D【解析】【分析】根据随机变量()0,1N，正态曲线关于0x=对称，得到对称区间对应的概率相等，根据大于1的概率得到小于1−的概率，根据对称轴一侧的区间的概率是12，即可求出结果.【详解】∵随机变量()0,1N，∴正

态曲线关于0x=对称，∵()1Pp=，∴()1Pp−=，∴()1102Pp−=−，故选：D.【点睛】本题主要考查了正态分布曲线的特点及曲线所表示的意义，考查正态曲线的对称性的应用，考查关于对称轴对称的区间

上的概率相等，本题属于基础题．7.1021001210(2).xaaxaxax−=++++则12310aaaa++++=()A.1B.1−C.1023D.1023−【答案】D【解析】【分析】令二项式中的1x

=，又由于所求之和不含0a，令0x=，可求出0a的值，代入即求答案．【详解】令1x=代入二项式1021001210(2)xaaxaxax−=++++，得100110(21)1aaa−=+++=，令0x=得01024a=，12

1010241aaa++++=，12101023aaa+++=−故选D．【点睛】本题主要考查二项式定理的应用，一般在求解有二项式关系数的和等问题时通常会将二项式展开式中的未知数x赋值为1或0或者是1−进行求解.本题属于基础题型．8.用火柴棒按如图的方法搭三

角形：按图示的规律搭下去，则第100个图形所用火柴棒数为（）A.401B.201C.402D.202【答案】B【解析】【分析】先设第n个图形所用火柴棒数为na，由图可知，数列na是以3为首项，2为公差的等差数列，再求解即可.【详解】解：设第n个图

形所用火柴棒数为na，则由图可知，数列na是以3为首项，2为公差的等差数列，则32(1)21nann=+−=+，即10021001201a=+=，故选：B.【点睛】本题考查了归纳推理能力，重点考查了等差数列通项公式的求法，

属基础题.9.已知函数()322fxxx=−，13,x−，则下列说法不正确．．．的是（）A.最大值为9B.最小值为3−C.函数()fx在区间1,3上单调递增D.0x=是它的极大值点【答案】C【解析】【分析】利用导数分析函数()yfx

=在区间1,3−上的单调性，求得该函数的极值与最值，由此可判断各选项的正误.【详解】()322fxxx=−，则()()23434fxxxxx=−=−.令()0fx，可得0x或43x；令()0fx，可得403x.当13,x−时，函数()yfx=在区间)1,0−,4,33

上均为增函数，在区间40,3上为减函数，C选项错误；所以0x=是函数()yfx=的极大值点，D选项正确；因为()00f=，()327299f=−=，()11213f−=−−=−，46416322327927f=−

=−，所以，函数()yfx=在区间1,3−上的最大值为9，最小值为3−，A、B选项正确.故选：C.【点睛】本题考查利用导数判断函数的单调性，以及利用导数求解函数的极值点与最值，考查分析问题和解决问题的能力，属于中等题.10.甲、乙二人争

夺一场围棋比赛的冠军，若比赛为“三局两胜”制，甲在每局比赛中获胜的概率均为34，且各局比赛结果相互独立.则在甲获得冠军的情况下，比赛进行了三局的概率为（）A.13B.25C.23D.45【答案】A【解析】【分析】记事件:A甲获得冠军，事件:B比赛进行三局，计算

出事件AB的概率和事件A的概率，然后由条件概率公式可得所求事件的概率为()()()PABPBAPA=.【详解】记事件:A甲获得冠军，事件:B比赛进行三局，事件:AB甲获得冠军，且比赛进行了三局，则第三局甲胜，前三局甲胜了两局，由独立事件的概率乘法公式得()12

313944432PABC==，对于事件A，甲获得冠军，包含两种情况：前两局甲胜和事件AB，()2392743232PA=+=，()()()932132273PABPBAPA==

=，故选A.【点睛】本题考查利用条件概率公式计算事件的概率，解题时要理解所求事件的之间的关系，确定两事件之间的相对关系，并利用条件概率公式进行计算，考查运算求解能力，属于中等题.11.设0＜a＜1，已知随机变量X的分布列是X0a1P131313若()16DX=，则a＝（）A.12B.1

3C.14D.15【答案】A【解析】【分析】先求出期望，利用方差公式求解可得结果．【详解】解：1111()013333aEXa+=++=，222111111()()()(1)333333aaaDXa+++=+−+

−2221[(1)(21)(2)]27aaa=++−+−22(1)9aa=−+16=，∴24443aa−+=，即()2210a−=，解得12a=．故选：A．【点睛】本题主要考查方差的求法，考查计算能力，属于中档题．12.点P是曲线2lnyxx=−上任意一

点，则点P到直线2yx=−的距离的最小值是（）A.1B.2C.2D.22【答案】B【解析】【分析】由题意可知，过点P的切线与直线2yx=−平行，由此可求出点P的坐标，然后利用点到直线的距离公式求解即可【详解】解：令121yxx=−=，则1x=，即(1,1)P，所以22

2d==，故选：B．【点睛】此题考查导数的几何意义的应用，考查点到直线的距离公式，属于基础题.二、填空题（本大题共4小题，每小题5分，共20分．）13.41()(1)xxx−−的展开式中3x的系数为______

_______.【答案】5【解析】【分析】将代数式变形为()()()44411111xxxxxxx=−−−−−，写出展开式的通项，令x的指数为3，求得参数的值，代入通项即可得解.【详解】()()()44411111xxxxxxx=−−−−−，展开式通项为

()()44111rrrrrrTxCxCx++==−−，()()411411kkkkkkCxTCxx+−=−−−=−令1313rk+=−=，可得24rk==，因此，展开式中3x的系数为24445CC−=

.故答案为：5.14.已知直线yxb=+是曲线3xye=+的一条切线，则b=________.【答案】4【解析】【分析】设切点为()00,+3xxe，根据导数的几何意义可求斜率0()1kfx==，即可求出0x，代入切线方程即可求解.【详解】设()3xfxe=+，切点

为()00,+3xxe，因为()xfxe=，所以01xe=，解得00x=，所以0034ye=+=，故切点为(0,4)，又切点在切线yxb=+上，故4b=.故答案为：4【点睛】本题考查导数的几何意义，考查运算求解能力，属于容易题.

15.有5名学生做志愿者服务，将他们分配到图书馆、科技馆、养老院这三个地方去服务，每个地方至少有1名学生，则不同的分配方案有____种（用数字作答）.【答案】150【解析】【分析】由题意可知，由两种分配方案分别为2，2，1型或3,1,1型，每一种分配全排即可.

【详解】解：将5名志愿者分配到这三个地方服务，每个地方至少1人，其方案为2，2，1型或3,1,1型．其选法有225322CCA或35C，而每一种选法可有33A安排方法，故不同的分配方案有223335335322CCACAA+=150种．故答案为150．【点睛】本题考查了排列与组合

的计算公式、“乘法原理”等基础知识与基本方法，属于中档题．16.观察下列各式：1ab+=，223ab+=，334ab+=，447ab+=，5511ab+=，则99ab+=_________．【答案】76【解析】【分析】从所给式子归纳呈现的规律，可得结论.

【详解】观察1ab+=，223ab+=，334ab+=，447ab+=，5511ab+=,不难发现后一项的数值是它前面相邻两项数值的和，所以6677889918,29,47,76,abababab+=+=+=+=故答案为76.【点睛】本题主要考查归纳推理，根据所给项观察出内含的规律是解决此类

问题的关键.三、解答题（共70分，解答应写出文字说明，证明过程或演算步骤）17.有甲、乙两个班级进行数学考试，按照大于等于85分为优秀，85分以下为非优秀统计成绩后，得到如下的列联表.优秀非优秀总计甲班10乙班30合计105已知从全部105人

中随机抽取1人为优秀的概率为27.（1）请完成上面的列联表；（2）根据列联表的数据，能否有95%的把握认为“成绩与班级有关系”？附：()()()()()22nadbcKabcdacbd−=++++，其中nabcd=++

+.()20PKk0.050.010k3.8416.635【答案】（1）表格见解析；（2）有95%的把握认为“成绩与班级有关系”.【解析】【分析】（1）根据优秀的概率为27可得乙班优秀的人数为20，即可得答案；（2）计算2K的值，再与3.841进行比较大小，即可得答案；【详

解】（1）列联表如下：优秀非优秀总计甲班104555乙班203050合计3075105（2）根据列联表中的数据，得()22105103020456.1093.84155503075K−=，因此有95%的把握认

为“成绩与班级有关系”.【点睛】本题考查列联表和卡方系数计算，考查数据处理能力，属于基础题.18.现有5名男生、2名女生站成一排照相,（1）两女生要在两端，有多少种不同的站法？（2）两名女生不相邻，有多少种不同的站法？（3）女生甲不在左端，女生乙不在右端，有多少种不同的站法

？【答案】（1）2400；（2）3600；（3）3720.【解析】试题分析：（1）分两步，两端的两个位置，女生任意排，有22A种排法，中间的五个位置男生任意排，有55A排法,利用分步计数乘法原理可得结果；（2）先将5名男生全排列，利

用插空法，把2名女生插入到5名形成的6个空中的2个即可；(3)采用去杂法，在七个人的全排列中，去掉女生甲在左端的66A个，再去掉女生乙在右端的66A个，但女生甲在左端同时女生乙在右端的55A种排除了两次，要找回来一次.试题解析：（1）两端的两个

位置，女生任意排，中间的五个位置男生任意排,25252400AA=（种）.（2）把男生任意全排列，然后在六个空中（包括两端）有顺序地插入两名女生；52563600AA=（种）.（3）采用去杂法，在七个人的全排列中，去掉女生甲在左端的66A个，再

去掉女生乙在右端的66A个，但女生甲在左端同时女生乙在右端的55A种排除了两次，要找回来一次．76576523720AAA−+=（种）.【方法点睛】本题主要考查分类计数原理与分步计数原理及排列组合的应用，属于难题.有关排列组合的综合问题，往往是两个原理及排列组合问题交叉应用才能解决问题，解答这

类问题理解题意很关键，一定多读题才能挖掘出隐含条件.解题过程中要首先分清“是分类还是分步”、“是排列还是组合”，在应用分类计数加法原理讨论时，既不能重复交叉讨论又不能遗漏，这样才能提高准确率.19.为保护农民种粮收益，促进粮食生产，确保国家粮食安全，调动广大农民粮食生

产的积极性，从2004年开始，国家实施了对种粮农民直接补贴.通过对2014～2018年的数据进行调查，发现某地区发放粮食补贴额x（亿元）与该地区粮食产量y（万亿吨）之间存在着线性相关关系.统计数据如下表：年份2014年2015年2016年2017年2018

年补贴额/x亿元91012118粮食产量/y万亿吨2325302621（1）请根据如表所给的数据，求出y关于x的线性回归直线方程ybxa=+；（2）通过对该地区粮食产量的分析研究，计划2019年在该地区发放粮食补贴额7亿元，请根据（1）中所得的线性回归直线方

程，预测2019年该地区的粮食产量.（参考公式：()()()121niiiniixxyybxx==−−=−，aybx=−）【答案】（1）2.14ˆyx=+（2）粮食产量大约为18.7万亿吨.【解析】【分析】（1）由最小二乘法求出a,b的估计值，进而可得回归直线方程；（2）将7

x=代入（1）所求的回归方程即可求出结果.【详解】（1）由已知数据，可得91012118105x++++==，2325302621255y++++==.代入公式()()121()ˆniiiniixxyybxx==−−=−，经计算，得ˆ2.1b=，∴ˆˆ4aybx=−=.∴所求y关于x

的线性回归直线方程为2.14ˆyx=+.（2）由题意，知7x=，代入（1）中所得线性回归直线方程2.14ˆyx=+，计算得ˆ18.7y=.∴2019年该地区的粮食产量大约为18.7万亿吨.【点睛】本题主要考查线性回归方程以及利用线性回归方程求预测值的问题，由最小二乘法先求出

a,b的估计值，进而即可求解，属于基础题型.20.港珠澳大桥是一座具有划时代意义的大桥.它连通了珠海香港澳门三地，大大缩短了三地的时空距离，盘活了珠江三角洲的经济，被誉为新的世界七大奇迹.截至2019年10月23日8点，珠海公路口岸共验放出入境旅客超过1400万人次，日均客流

量已经达到4万人次，验放出入境车辆超过70万辆次，2019年春节期间，客流再次大幅增长，日均客流达8万人次，单日客流量更是创下11.3万人次的最高纪录.2019年从五月一日开始的连续100天客流量频率分布直方图如下（1）①同一组数据用该区间的中

点值代替，根据频率分布直方图.估计客流量的平均数.②求客流量的中位数.（2）设这100天中客流量超过5万人次的有n天，从这n天中任取两天，设X为这两天中客流量超过7万人的天数.求X的分布列和期望．【答案】（1）

①4.15，②4.125；（2）分布列见解析，()23EX=【解析】【分析】（1）①根据频率分布直方图估计平均数的方法，计算出平均数；②根据频率分布直方图估计中位数的方法，计算出中位数；（2）根据超几何分布

的分布列和数学期望的计算方法，计算出X的分布列和期望.【详解】（1）①平均值为()2.50.23.50.254.50.45.50.056.50.057.50.0514.15+++++=②设中位数为x，则()0.200.2

50.4040.5x++−=解得中位数为4.125x=（2）可知15n=其中超过7万人次的有5天()2010521545301057CCPXC====()111052155010110521CCPXC====()021052

15102210521CCPXC====X012P371021221所以()31022012721213EX=++=【点睛】本小题主要考查利用频率分布直方图估计平均数和中位数，考查超几何分布的分布列和期望的计算，属于基础题.21.已知函数()2xfxex=−()1求

曲线()yfx=在点()()0,0f处的切线方程;()2若函数()()gxfxa=−，1,1x−恰有2个零点，求实数a的取值范围【答案】(1)x+y-1=0.(2)22ln22ae−−.【解析】【分析】(1)求得f（x）的导数，

可得切线的斜率和切点，即可得到所求切线方程；(2)函数()(),1,1gxfxax=−−恰有2个零点转化为两个图象的交点个数问题，数形结合解题即可.【详解】（1）因为()e2xfxx=−，所以()e2xfx=−.所以()01.f

=−又()01,f=所以曲线()yfx=在点()()0,0f处的切线方程为1,yx−=−即10xy+−=.（5分）（2）由题意得，()e2xgxxa=−−，所以()e2xgx=−.由()e20xgx=−=，

解得ln2x=，故当1ln2x−时，()0gx，()gx在)1,ln2−上单调递减；当ln21x时，()0gx，()gx在(ln2,1上单调递增.所以()()minln222ln2gxga==−−.又()11e+2ga−−=−，()1e

2ga=−−，若函数恰有两个零点，则()()()11e20,1e20,ln22220,gagaglna−−=+−=−−=−−解得22ln2e2a−−.所以实数a的取值范围为(22ln2,e2−−.【点睛】本题考查函数零点问题.函数零点问题有两种解

决方法，一个是利用二分法求解，另一个是化原函数为两个函数，利用两个函数的交点来求解.22.已知函数()()11lnaxaxxfx=++−．（1）当2a=时，求曲线()yfx=在1x=处的切线方程；（2）若0a，讨论函数()fx的单调性．【答案】（

1）3y=；（2）答案见解析.【解析】【分析】（1）根据导数的几何意义得到()()10,13ff−==，进而得到切线方程；（2）对函数求导，研究导函数的正负，得到函数的单调性.【详解】（1）当2a=时，()12lnfxxxx=+−，()2112xfxx−=−，又()10

f=，()13f=，所以曲线()fx在1x=处的切线方程为3y=．（2）()()()()2222111111axaxxaxaaxxxxfx+−−−+−=−+==（0x），①当0a=时，()fx在()0,1上单调递减，在()1,+上单调递增；②当10a−时，()fx在()0,

1和1,a−+上单调递减，在11,a−上单调递增；③当1a=−时，()fx在()0,+上单调递减；④当1a−时，()fx在10,a−和()1,+上单调递减，在

1,1a−上单调递增．【点睛】本题考查的是导数的几何意义，切线方程的求法；考查了导数在研究函数的单调性中的应用；一般在研究函数的单调性中，常见的方法有：图象法，通过图象得到函数的单调区间；通过研究函数的导函数

的正负得到单调性．