【文档说明】第3练 等可能条件下的概率(二)(培优练习)-【多维练】2021-2022学年九年级数学上学期多维课时提优＋阶段提优(苏科版)(解析版).docx，共(12)页，313.314 KB，由envi的店铺上传

转载请保留链接：https://www.doc5u.com/view-ce1fa390f787f0bd8dbda48171c09624.html

以下为本文档部分文字说明：

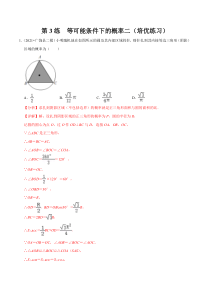
第3练等可能条件下的概率二（培优练习）1．（2021•广饶县二模）小明随机地在如图所示的圆及其内部区域投针，则针扎到其内接等边三角形（阴影）区域的概率为（）A．B．C．D．【分析】求扎到阴影区域（不包括边界）的概率就是正三角形面积与圆的面积的比．【详解】解：设扎到阴影区域的正

三角形的概率为P，圆的半径为R，记圆的圆心为点O，过O作OD⊥BC与D，连接OA，OB，OC，∵△ABC是正三角形，∴AB＝BC＝AC，∴∠AOB＝∠BOC＝∠COA，∴∠BOC＝＝120°，∵OB＝OC

，∴∠BOD＝×120°＝60°，∴∠OBD＝30°，∵OB＝R，∴OD＝，BD＝OBcos30°＝R，∴BC＝2BD＝R，∴S△BOC＝BC•OD＝，∵OA＝OB＝OC，∠AOB＝∠BOC＝∠AOC，∴△AOB≌△BOC≌△COA（SAS），∴

S△AOB＝S△BOC＝S△COA，∴S△ABC＝3S△BOC＝，∵S圆＝πR2，∴P＝＝．故选：C．2．如图是一块三角形纸板，其中AD＝DF，BE＝ED，EF＝FC，一只蚂蚁在这块纸板上爬行，则蚂蚁踩到阴影部分的概率为（）A．B．C．D．【分析】利

用等底同高的三角形面积相等的概念，将△ABC分为7个面积相同的三角形，中间阴影部分的三角形的面积是△ABC的，所以蚂蚁踩到阴影部分的概率是．【详解】解：连接AE，BF，CD，∵AD＝DF，BE＝ED，EF＝FC，利用三角形中线的性质可得，∴S△A

DC＝S△CDF，S△AED＝S△ABE，S△BEF＝S△EFD，S△EBF＝S△BFC，S△ABD＝S△BDF，S△AEF＝S△AFC，∴△ABC被分为7个面积相同的三角形，中间阴影部分的三角形的面积是△ABC的，所

以蚂蚁踩到阴影部分的概率是，故选：B．3．（2021•烟台）连接正六边形不相邻的两个顶点，并将中间的六边形涂成黑色，制成如图所示的镖盘，将一枚飞镖任意投掷到镖盘上，飞镖落在黑色区域的概率为（）A．B．C．D．【分析】如图，将阴影部分分割成图形中小三角形的大小，令小三角形的面积

为a，分别表示出阴影部分的面积和正六边形的面积，根据概率公式求解即可．【详解】解：如图所示，令S△ABC＝a，则S阴影＝6a，S正六边形＝18a，∴将一枚飞镖任意投掷到镖盘上，飞镖落在黑色区域的概率为＝，故选：B．4．（2021秋•市南区期中）斐波那契螺旋线，也

称“黄金螺旋线”，是根据斐波那契数列1，1，2，3，5，画出来的螺旋曲线．如图，白色小圆内切于边长为1的正方形，黑色曲线就是斐波那契螺旋线，它是依次在以1，2，3，5为边长的正方形中画一个圆心角为90°的扇形，将其圆弧连接起来得到的．若在矩形

ABCD内随机取一点，则此点取自阴影部分的概率是（）A．B．C．D．【分析】根据已知条件可知，矩形ABCD的长为8，宽为5，即面积S矩＝8×5＝40，阴影部分的面积S阴＝（1﹣）++++＝+1，然后根据概率公式即可得出答案

．【详解】解：根据已知可得：矩形ABCD的长为8，宽为5，即面积S矩＝8×5＝40，阴影部分的面积S阴＝（1﹣）++++＝+1，设在矩形ABCD内随机取一点，则此点取自阴影部分为事件A，则此点取自阴影部分的概率是＝．故选：D．5．如图，正方形ABCD是大圆的内接四

边形，阴影部分是正方形除内接圆外的部分，将一个飞镖随机投掷到大圆形纸板上，则飞镖落在阴影区域的概率是（）A．B．C．D．【分析】连接BD、AC，它们相交于O点，过O点作OD⊥AB于D，如图，设OD＝r，利用正方形的内切圆的性质得到正方形ABCD的内切圆的半径为r，所以AB＝2r，O

B＝r，然后用阴影部分的面积除法大圆的面积可得到镖落在阴影区域的概率．【详解】解：连接BD、AC，它们相交于O点，过O点作OD⊥AB于D，如图，设OD＝r，即正方形ABCD的内切圆的半径为r，则AB＝2OD＝2r，∴OB＝OD＝r，∴镖落

在阴影区域的概率＝＝．故选：A．6．如图，一块菱形地，AB＝4m，∠A＝60°，以A点为圆心，AB为半径画弧AD于点D，一只小狗在地面上随意跑动，当它停止时站在黑色区域的概率是．【分析】根据菱形的性质得到AD＝AB＝4

m，过D作DE⊥AB于E，得到DE＝AD＝2（m），求得黑色区域的面积，然后根据概率公式求出概率即可．【详解】解：∵四边形ABCD是菱形，∴AD＝AB＝4m，过D作DE⊥AB于E，∴∠AED＝90°，∵∠A＝60°，∴

DE＝AD＝2（m），∴黑色区域的面积＝S菱形ABCD﹣S扇形ABD＝4×2﹣＝（8﹣）m2，∴它停止时站在黑色区域的概率是＝＝1﹣，故答案为：1﹣．7．（2021•双流区模拟）如图所示，四个正六边形的面积都是相等的，现随机向读图形内掷一枚小针，则针尖落在阴

影区域的概率为．【分析】令中间小菱形的面积为a，再表示出所有面积和阴影部分的面积，根据概率公式求解即可．【详解】解：令中间小菱形的面积为a，则四个正六边形加中间小菱形的面积为13a，则阴影部分的面积为4a，所以针尖落在阴影区域的概率为＝，故答案为：．8．（202

0秋•商城县期末）如图所示的是边长为4的正方形镖盘ABCD，分别以正方形镖盘ABCD的三边为直径在正方形内部作半圆，三个半圆交于点O，乐乐随机地将一枚飞镖投掷到该镖盘上，飞镖落在阴影区域的概率为．【分析】根据正方形被均分成4等份，飞镖落在每一个区域的机会是均等

的，由此计算出阴影区域的面积，利用几何概率的计算方法详解即可．【详解】解：如图，连接AC，BD，∵正方形被均分成4等份，飞镖落在每一个区域的机会是均等的，其中阴影区域的面积占了其中的2等份，∴P（飞镖落在阴影区域）＝＝．故答案为：．9．（2017•涪城区校级

自主招生）如图，点D、E、F是△ABC三边的中点，点M、N、P是△DEF三边的中点，将△FPM与△ECD涂成阴影，假设△ABC内任意一点被取到的机会均等，那么在△ABC内随机取一个点，这个点恰好落在阴影部分的概率为．【分析】由D、E分别是

BC、AC的中点知DE是△ABC的中位线，证△CDE∽△CBA得S△CDE＝S△CBA，同理S△FPM＝S△FDE＝S△CBA，继而知S△FPM+S△CDE＝S△CBA，据此可得答案．【详解】解：∵D、E分别是BC、AC的中点，∴DE是△ABC的中位线，∴DE∥AB，且DE＝

AB，∴△CDE∽△CBA，∴S△CDE＝S△CBA，同理，S△FPM＝S△FDE＝S△CBA，∴S△FPM+S△CDE＝S△CBA，则＝．故答案为：．10．（2020秋•鼓楼区校级月考）如图，在一块边长为

30cm的正方形飞镖游戏板上，有一个半径为10cm的圆形阴影区域，飞镖投向正方形游戏板的任何位置的机会均等，则飞镖落在阴影区域内的概率为（结果保留π）．【分析】用圆的面积除以正方形的面积即可求得答案．【详解】解：P（飞镖落在阴影区域内）＝＝．故答案为：．11．（2019•秦淮区校级模拟）

在边长为4的正方形平面内，建立如图1所示的平面直角坐标系．学习小组做如下实验：连续转动分布均匀的转盘（如图2）两次，指针所指的数字作为直角坐标系中P点的坐标（第一次得到的数为横坐标，第二次得到的数为纵坐标）．（1）转盘转动共能得到个不同点，P点落在正方形边上的概

率是；（2）求P点落在正方形外部的概率．【分析】（1）根据题意先列出图表，得出转盘转动共能得到的不同的点数和P点落在正方形边上的点数，再根据概率公式即可得出答案；（2）根据图表得出总点数和落在正方形外

部的点数，然后根据概率公式即可得出答案．【详解】解：（1）列表如下：123﹣1﹣2﹣31（1，1）（1，2）（1，3）（1，﹣1）（1，﹣2）（1，﹣3）2（2，1）（2，2）（2，3）（2，﹣1）（2，﹣2）（2，﹣3）3（3，1）（3，2）（3，3）（3，﹣1）（3，﹣2）

（3，﹣3）﹣1（﹣1，1）（﹣1，2）（﹣1，3）（﹣1，﹣1）（﹣1，﹣2）（﹣1，﹣3）﹣2（﹣2，1）（﹣2，2）（﹣2，3）（﹣2，﹣1）（﹣2，﹣2）（﹣2，﹣3）﹣3（﹣3，1）（﹣3，2）（﹣3，3）

（﹣3，﹣1）（﹣3，﹣2）（﹣3，﹣3）根据图表可得：转盘转动共能得到36个不同点，P点落在正方形边上的有12个，则P点落在正方形边上的概率是＝；故答案为：36，；（2）根据图表得出：共有36个点，其中落在正方形外部的点共有20个，则P点落在正方形外部的概率是：＝．12．（2021•江岸区

校级自主招生）如图①，在Rt△ABC中，∠C＝90°，两条直角边长分别为a，b，斜边长为c．如图②，现将与Rt△ABC全等的四个直角三角形拼成一个正方形EFMN．（1）若Rt△ABC的两直角边之比均为2：3．现随机向该图形内掷一枚小针，则针尖落在四个直角三角形区域的概率是

多少？（2）若正方形EFMN的边长为8，Rt△ABC的周长为18，求Rt△ABC的面积．【分析】（1）根据勾股定理得到c，根据概率公式即可得到结论；（2）根据题意求出c，得到a+b的值，根据三角形的面积公式、完全平方公式计算，得到答案．【详解】

解：（1）∵Rt△ABC的两直角边之比均为2：3，∴设b＝2k，a＝3k，由勾股定理得，a2+b2＝c2，∴c＝k，∴针尖落在四个直角三角形区域的概率是＝；（2）∵正方形EFMN的边长为8，即c＝8，∵Rt△ABC的周长为18，∴a+b+c＝18，

∴a+b＝10，则Rt△ABC的面积＝ab＝[（a+b）2﹣（a2+b2）]＝9．13．如图是计算机中的一种益智小游戏“扫雷”的画面，在一个9×9的小方格的正方形雷区中，随机埋藏着10颗地雷，每个小方格

内最多只能埋藏1颗地雷．小红在游戏开始时首先随机地点击一个方格，该方格中出现了数字“3”，其意义表示该格的外围区域（图中阴影部分，记为A区域）有3颗地雷；接着，小红又点击了左上角第一个方格，出现了数字“1”，其外围区域（图中阴影部分）记为B区域；“A区域与B区域以及出现数

字‘1’和‘3’两格”以外的部分记为C区域．小红在下一步点击时要尽可能地避开地雷，那么她应点击A、B、C中的哪个区域？请说明理由．【分析】根据几何概率，求出地雷数埋有地雷的区域的面积之比，即为遇到地雷的概率，然后比较概率的大小．【详解】解：

∵，，，（6分）∵，，∴P（A）＞P（B）＞P（C），∴小红点击C区域．（8分）14．如图，放在直角坐标系的正方形ABCD边长为4，现做如下实验：抛掷一枚均匀的正四面体骰子（它有四个顶点，各顶点的点数分别是1至4这四

个数字中一个），每个顶点朝上的机会是相同的，连续抛掷两次，将骰子朝上的顶点数作为直角坐标系中P点的坐标（第一次的点数作横坐标，第二次的点数作纵坐标）．（1）求P点落在正方形ABCD面上（含正方形内部和边界）的概率．（2）将正方形ABCD平移整数个单位，则是否存在一种平移，使点P落在正方

形ABCD面上的概率为0.75；若存在，指出其中的一种平移方式；若不存在，请说明理由．【分析】（1）依题意得点P的横坐标有数字1，2，3，4四种选择，纵坐标也有数字1，2，3，4四种选择，故点P的坐标共有16种等可能的情况，有四种等可能情况将落在正方形ABCD上，所以概率为．（2）

要使点P落在正方形面上的概率为，所以要将正方形移动使之符合．【详解】解：（1）根据题意，点P的横坐标有数字1，2，3，4四种选择，点P的纵坐标也有数字1，2，3，4四种选择，所以构成点P的坐标共有4×4＝16种等可能的情况．如下图所示：其中点P的（1，1），（1，

2），（2，1），（2，2）四种等可能的情况将落在正方形ABCD面上，故所求的概率为＝．（2）因为要使点P落在正方形ABCD面上的概率为＝＞，所以只能将正方形ABCD向上或向右整数个单位平移，且使点P落在正方形面上的数目为

12．∴存在满足题设要求的平移方式：先将正方形ABCD上移2个单位，后右移1个单位（先右后上亦可）；或先将正方形ABCD上移1个单位，后右移2个单位（先右后上亦可）．