【文档说明】四川省宜宾市第四中学校2023届高三二诊模拟理科数学试题 .docx，共(6)页，493.594 KB，由小赞的店铺上传

转载请保留链接：https://www.doc5u.com/view-c36bbae255293c16a8a505dd89bf04c4.html

以下为本文档部分文字说明：

宜宾市四中高2020级高三二诊模拟考试数学（理工类）注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上．2．本试卷满分150分，考试时间120分钟．考试结束后，请将答题卡交回．第I卷选择题一．选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个

选项中，只有一项是符合题目要求的．1.已知集合{|(3)(2)0}Axxx=+−，13Bxx=−，则AB=（）A.()1,2-B.()1,3−C.()2,3D.()0,32.设复数z满足12i1iz+=−，则z=（）A.5B.52C.10D.1023.已知等比数列na的前n项和为

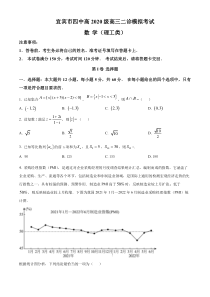
nS，且55S=，1030S=，则15S=.A90B.125C.155D.1804.采购经理指数（PMI），是通过对企业采购经理的月度调查结果统计汇总、编制而成的指数，它涵盖了企业采购、生产、流通等各个环节，包括制造业和非制造业领域，是国际上通用的检测宏观经济走势的先行指数之一，具有较强的预测、预

警作用．制造业PMI高于50%时，反映制造业较上月扩张；低于50%，则反映制造业较上月收缩．下图为我国2021年1月—2022年6月制造业采购经理指数（PMI）统计图．根据统计图分析，下列结论最恰当的一

项为（）.A.2021年第二、三季度各月制造业在逐月收缩B.2021年第四季度各月制造业在逐月扩张C.2022年1月至4月制造业逐月收缩D.2022年6月PMI重回临界点以上，制造业景气水平呈恢复性扩张5.若5a

xx+的展开式中x的系数为15，则=a（）A.2B.3.C.4D.56.已知双曲线2222:1(0,0)xyCabab−=的一条渐近线方程为52yx=−，则双曲线C的离心率为（）A.5

2B.32C.355D.237.在长方体1111ABCDABCD−中，已知异面直线1AC与AD，1AC与AB所成角的大小分别为60和45，则直线1BD和平面1ABC所成的角的余弦值为（）A33B.12

C.32D.638.某大学计算机学院的薛教授在2019年人工智能方向招收了6名研究生.薛教授欲从人工智能领域的语音识别、人脸识别，数据分析、机器学习、服务器开发五个方向展开研究，且每个方向均有研究生学习，其中刘泽同学学习人脸识

别，则这6名研究生不同的分配方向共有（）A.480种B.360种C.240种D.120种9.若函数()2()fxxxa=+在1x=处有极大值，则实数a的值为（）A.1B.1−或3−C.1−D.3−10.某地锰矿石原有储量为a

万吨，计划每年的开采量为本年年初储量的m（01m，且m为常数）倍，那么第n（*nN）年在开采完成后剩余储量为()1nam−，并按该计划方案使用10年时间开采到原有储量的一半．若开采到剩余储量为原有储量的70%时，则需开采约（）年．（参考数据：21.4）A4B.5C.

6D.811.某四棱锥的底面为正方形，顶点在底面的射影为正方形中心，该四棱锥内有一个半径为1的球，则该四棱锥的表面积最小值是（）A.16B.8C.32D.24的..12.已知函数()fx=1ln,0,e,0.xxxxxx+则关于x的方程2()()10()efxaf

xaR−−=的解的个数的所有可能值为（）A.3或4或6B.1或3C.4或6D.3第2卷非选择题二、填空题：本大题共4个小题，每小题5分，共20分．13.曲线()ln32fxxx=+−在点()()1,1f处的切线方程为_______．14.两个非零向量a，b，定义||||||sin,ab

abab=．若(1,0,1)a=，(0,2,2)b=，则ab=___________．15.2021年第31届世界大学生夏季运动会将在成都举行．为营造“爱成都迎大运”全民运动和全民健身活动氛围，某社区组织甲、乙两队进行一场足

球比赛，根据以往的经验知，甲队获胜的概率是25，两队打平的概率是110，则这次比赛乙队不输的概率是_______________________．16.已知函数()sinsin2fxxx=，0,2πx.下列有关()fx的说法中，正确的是______(填写你认为正确的序

号).①不等式()0fx的解集为π04xx或3ππ4x；②()fx在区间0,2π上有四个零点；③()fx的图象关于直线πx=对称；④()fx的最大值为439；⑤()fx的最小值为32−；三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17

~21题为必考题，每个试题考生都必须答．第22、23题为选考题，考生根据要求作答．（一）必做题：共60分．17.在ABC中，角,,ABC所对的边分别为,,abc，且满足cos2acCbb=−（1）求角B;（2）若

ABC外接圆的半径为3，且AC边上的中线长为172，求ABC的面积18.一网络公司为某贫困山区培养了100名“乡土直播员”，以帮助宣传该山区文化和销售该山区的农副产品，从而带领山区人民早日脱贫致富．该

公司将这100名“乡土直播员”中每天直播时间不少于5小时的评为“网红乡土直播员”，其余的评为“乡土直播达人”．根据实际评选结果得到了下面22列联表：网红乡土直播员乡土直播达人合计男104050女203050合计3070100

（1）根据列联表判断是否有95%的把握认为“网红乡土直播员”与性别有关系？（2）在“网红乡土直播员”中按分层抽样的方法抽取6人，在这6人中选2人作为“乡土直播推广大使”．设被选中的2名“乡土直播推广大使”中男性人数为，求的分布列和期望．附：()()()()()22nadb

cKabcdacbd−=++++，其中nabcd=+++．()20PKk0.150.100.050.0250.0100.0050.0010k2.0722.7063.8415.0246.6357.87910.8

2819.如图，四棱锥PABCD−中，PA⊥底面ABCD，//ADBC，2ABC=，122ABBCAD===，且PAa=，E，F分别为PC，PB的中点.（1）若2a=，求证：PB⊥平面ADEF；（2）若四棱锥PABCD−的体积为2，求二面角APDC−−的余弦值.20.在平面直角坐标系xOy中

，直线()10ykxk=+与抛物线C：()240xpyp=交于A，B两点，且当1k=时，8AB=.（1）求p的值；（2）设线段AB的中点为M，抛物线C在点A处的切线与C的准线交于点N，证明：//MNy轴.21已知函数()221xfxxeaxax=++−．（1）当212a

e=时，求()fx在2x=−处的切线方程；（2）当11ae−−时，讨论()fx零点的个数．（二）选做题：共10分．请考生在第22、23题中任选一题作答．如果多做，则按所做的第一题记分．选修4-4：坐标系与参数方程22.在平面直角坐标系xOy中，曲线1C是圆心在()0,2，半径为2的

圆，曲线2C的参数方程为22cos22sin4xtyt==−（t为参数且02t），以坐标原点O为极点，x轴正半轴为极轴建立极坐标系．（1）求曲线1C的极坐标方程；（2）若曲线

2C与坐标轴交于A、B两点，点P为线段AB上任意一点，直线OP与曲线1C交于点M（异于原点），求OMOP的最大值．选修4-5：不等式选讲23.已知函数()22fxxx=−++.（1）求不等式()24fxx+的解集；.获得更多资源请扫码加入享学资源网微信公众号www.xiangxue10

0.com