【文档说明】《数学北师大版必修4教学教案》1.6.1余弦函数的图像 （8）含答案【高考】.doc，共(3)页，99.500 KB，由小赞的店铺上传

转载请保留链接：https://www.doc5u.com/view-b22afcc7de2cc6f611085e76044a8f1d.html

以下为本文档部分文字说明：

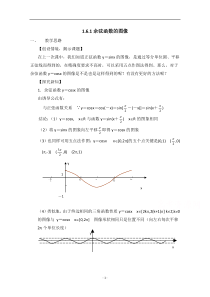
-1-1.6.1余弦函数的图像一、教学思路【创设情境，揭示课题】在上一次课中，我们知道正弦函数y＝sinx的图像，是通过等分单位圆、平移正弦线而得到的，在精确度要求不高时，可以采用五点作图法得到。那么，对于余弦函数y＝cosx的图像是不是也是这样得到的呢？有没有更好的方法呢？

【探究新知】1．余弦函数y＝cosx的图像由诱导公式有：与正弦函数关系∵y＝cosx＝cos(－x)＝sin[2－(－x)]＝sin(x＋2)结论：（1）y＝cosx,xR与函数y＝sin(x＋2)xR的图象相同（2

）将y＝sinx的图象向左平移2即得y＝cosx的图象（3）也同样可用五点法作图：y＝cosxx[0,2]的五个点关键是(0,1)(2,0)(,-1)(23,0)(2,1)（4）类似地，由于终边相同的三

角函数性质y＝cosxx[2k,2(k+1)]kZ,k0的图像与y＝cosxx[0,2]图像形状相同只是位置不同（向左右每次平移2π个单位长度）yxo1-12232−2yx1－1x6

yo--12345-2-3-41xy-2-2．余弦函数y＝cosx的性质观察上图可以得到余弦函数y＝cosx有以下性质：（1）定义域：y=cosx的定义域为R（2）值域：y=cosx的值域为[－1,1]，即有|cosx|≤1（有界性）(

3)最值：1对于y＝cosx当且仅当x＝2k,kZ时ymax＝1当且仅当时x＝2k＋π,kZ时ymin＝－12当2k-2<x<2k+2(kZ)时y=cosx>0当2k+2<x<2k+23(kZ)时y=cosx

<0(4)周期性：y＝cosx的最小正周期为2(5)奇偶性cos(－x)＝cosx(x∈R)y＝cosx(x∈R)是偶函数(6)单调性增区间为[（2k－1）π，2kπ]（k∈Z），其值从－1增至1；减区间为[2kπ，（2k＋1）π]（k∈Z），其值从1减至－1。【巩固

深化，发展思维】1．例题讲评例1．请画出函数y＝cosx－1的简图，并根据图像讨论函数的性质。解：（略，见教材P31-32）2．课堂练习二、归纳整理，整体认识（1）请学生回顾本节课所学过的知识内容有哪些？所涉

及的主要数学思想方法有那些？（2）在本节课的学习过程中，还有那些不太明白的地方，请向老师提出。（3）你在这节课中的表现怎样？你的体会是什么？三、布置作业：四、课后反思-3-