【文档说明】2019苏科版八年级上册数学第2章 2. 4 线段、角的轴对称性（第1课时）.doc，共(5)页，602.686 KB，由管理员店铺上传

转载请保留链接：https://www.doc5u.com/view-6050e266d1e4851efd3655af82728817.html

以下为本文档部分文字说明：

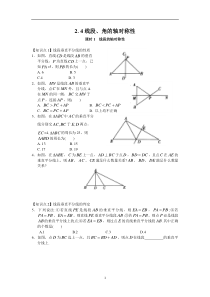
12.4线段、角的轴对称性课时1线段的轴对称性【知识点1】线段垂直平分线的性质1．如图，直线CD是线段AB的垂直平分线，P为直线CD上一点，已知PA=5，则PB的长为()A.6B.5C.4D.32．如图，MN是线段AB的垂直平分线，点C在

MN外，且与点A在MN的同一侧，BC交MN于点P，连接AP，则()A.BCPCAP+B.BCPCAP+C.BCPCAP=+D.以上均不正确3．如图，在ABC中AC的垂直平分线分别交,ACBC于,ED两点，EC=4,ABC的周长为23，则ABD的周长为()A.13B.15C

.17D.194．如图，在ABE，C为BE上一点，ADBC⊥于点D，BDDC=，且点C在AE的垂直平分线上，则AB，AC，CE满足什么数量关系?AB，BD，DE满足什么数量关系?【知识点2】线段垂直平分线的判定5．下列说法:①若

直线PE是线段AB的垂直平分线，则EAEB=，PAPB=;②若PAPB=，EAEB=，则直线PE垂直平分线段AB;③若PAPB=，则点P必是线段AB的垂直平分线上的点;④若EAEB=，则过点E的直线垂直平分线段AB.其中正确的个数是()A.1

B.2C.3D.46．如图，点D为BC边上一点，且BCBDAD=+，则点D在线段的垂直平分线上.27．在同一平面上有,,,ABCD四点，在平面上一定能找到一个点M，使MAMB=，MCMD=吗?.(填“一定能”或“不一定能”)8．如图，四边形ABCD是一只风筝的“骨架”，

其中ABAD=，CBCD=.(1)八年级的王芸同学观察了这只风筝的“骨架”后，她认为四边形ABCD的两条对角线ACBD⊥，垂足为E，且BEED=，你同意王芸同学的判断吗?请说明理由.(2)设对角线ACa=，B

Db=，用含,ab的式子表示四边形ABCD的面积.【知识点3】线段垂直平分线的作法9．如图，已知ABC(ACABBC)，用尺规在线段BC上确定一点P，使得PAPCBC+=，则符合要求的作图痕迹是()10．如图，按以下步骤作图:①分别以点B，C为圆心，大于12BC的长为半径画弧，两

弧相交于点M，N;②作直线MN交AB于点D，连接CD.则下列结论正确的是()A.点D为AB的中点B.BDDC=C.DCAC=D.//MNAC11．某旅游景区内有一块三角形绿地ABC，如图所示，现要在道路AB的边上建一个休息点M，使它到,AC两点的距离相等.在图中确定休息点M的位置.(保留作图

痕迹，不3写作法)【精选作业】1.如图，有,,ABC三个居民小区，现决定在三个小区之间修建一个购物超市，使超市到三个小区的距离相等，则超市应建在()A.,ACBC两边高线的交点处B.,ACBC两边垂直平分线的交点处C.,ACBC两边中线的交点处D.A，B平分线的交点处2.如图，在ABC中，

分别以点A和点B为圆心，大于12AB长为半径画弧，两弧相交于点M，N，作直线MN，交BC于点D，连接AD.若ADC的周长为10，7AB=，则ABC的周长为()A.7B.14C.17D.203.如图，ABC的周长为3

0cm，把ABC翻折，使点C和点A重合，折痕交BC于点D，交AC于点E，若4AE=cm，则ABD的周长是()A.22cmB.20cmC.18cmD.15cm4.如图，在ABC中，ABAC=，D是BC的中点，AC的垂直平分线分别交AC，AD，AB点,,EOF

，则图中的全等三角形共有()A.1对B.2对C.3对D.4对5.如图，点P在AOB的内部，点,MN分别是点P关于射线,OAOB的对称点，线段4MN分别交,OAOB于点,EF，若PEF的周长是20cm，则线

段MN的长是cm.6.如图，在四边形ABCD中，//ADBC，E为CD的中点，连接AE，BE，BEAE⊥，延长AE交BC的延长线于点F.求证：（1）FCAD=;（2）ABBCAD=+.7.如图，D是ABC的边BC的中点，过AD延长线上的点E作AD的垂线EF，垂足为E，EF与A

B的延长线交于点F，点O在AD上，AOCO=，//BCEF.求证：（1）ABAC=;（2）点O是ABC三边垂直平分线的交点.2.4线段、角的轴对称性课时1线段的轴对称性1.B2.C3.B4.ABACCE==ABBDDE+=5.C6.AC7.不一定能8.(1)同意.

理由如下:ABAD=Q,点A在BD的垂直平分线上.CBCD=Q,点C在BD的垂直平分线上.5直线AC为线段BD的垂直平分线，,BEDEACBD=⊥.(2)12ab9.D10.B11.作线段AC的垂直平分线交AB于点M

，则点M即所求.【精选作业】1.B2.C3.A4.D5.206.(1)//,ADBCADCFCE=Q()ADEFCEASAFCAD=(2)由(1)知AEFE=,ABFBBCCF==+,ADFCABBCAD==+Q7.(

1)DQ是ABC的边BC的中点，.BDCD=.,90ADEFAEF⊥=Q，//,90,BCEFADBAEFADBC==⊥Q,ABAC=.(2)连接BO.AOCO=Q,点O在AC的垂直平分线上.由(1)知AD垂直平分,BCBOCO=,点

O在BC的垂直平分线上，,AOCOBOCO==Q,AOBO=,点O在AB的垂直平分线上.点O是ABC三边垂直平分线的交点.