【文档说明】2021-2022学年高一数学人教A版必修1教学教案：2.3.1 幂函数 含解析【高考】.doc，共(6)页，578.000 KB，由小赞的店铺上传

转载请保留链接：https://www.doc5u.com/view-539632508006c9e6ce16e4e070c7e26d.html

以下为本文档部分文字说明：

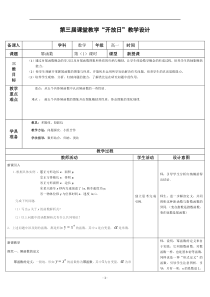
-1-第三届课堂教学“开放日”教学设计备课人学科数学年级高一时间课题幂函数第（1）课时课型新授课三维目标（1）通过对幂函数概念的学习以及对幂函数图象和性质的归纳与概括，让学生体验数学概念的形成过程，培养学生的抽象概括能力。（2）使学生理解并掌握幂函

数的图象与性质，并能初步运用所学知识解决有关问题，培养学生的灵活思维能力。（3）培养学生观察、分析、归纳问题的能力，了解类比法在研究问题中的作用。教学重点难点重点：从五个具体幂函数中认识幂函数的一些性质．难点：画五个具体幂函数的图象并由图象概括其性质，体会图象的变

化规律．学具准备教具：多媒体，投影仪教学方法：问题探究、小组合作学法指导：数形结合，归纳，类比教学过程教师活动学生活动设计意图新课引入1.根据具体实例：①正方形边长x，面积y；②正方体棱长x，体积y；③正方形面积x，边长y；④某人骑车x秒内匀速前进了1

m,骑车速度为y；⑤一物体位移y与位移时间x，速度1m/s.完成下列问题：（1）写出y关于x的函数解析式？（2）以上问题中的函数解析式有什么共同特征？2．上述问题中涉及到的函数，都是形如xy=的函数，其中x是自变量，

是常数．独立思考完成引例．师：引导学生分析归纳概括得出结论．师生：进一步解读定义，共同辨析这种新函数与指数函数的异同．（变在指数是指数函数，变在底数是幂函数）新课教学探究一、幂函数的定义幂函数的定义：一般地，形如xy=的函数称为幂函数，其中x为自变量，为常师：说

明：幂函数的定义来自于实践，它同指数函数、对数函数一样，也是基本初等函数，同样也是一种“形式定义”的函数，引导学生注意辨析．引导：只有一项，x的系数是1，-2-数．思考：幂函数解析式的特征？辨一辨：判断下列函数是否为幂函数.（1）4xy=（2）21xy=（3）22xy=（4）23+=x

y探究二、幂函数的图象与性质下面我们利用实例中的这五个幂函数，归纳学习幂函数的一些性质．画出下列函数的图象：观察解析式结构完成辨一辩练习整体系数是1辨一辩：生对幂函数定义的理解（理解3个1）师：教师用计算机作图，给学生展示标准的图像，强调画图象易犯的错误．（1）xy=

；（2）21xy=；（3）2xy=；（4）1−=xy；（5）3xy=．.思考1.观察图象，总结填写下表：分4个小组分别利用所学知识和方法尝试画出4个具体幂函数的图象，观察图象，体会幂函数的变化规律过程：1.各小组代表发言:投影自己画的函数图像归纳

函数有关性质，其他同学做好笔记2.可以有其他同学补充发言3共同讨论、评析．完成表格的填写.师：引导学生回顾讨论函数性质的方法.并指出函数单调性是判别大小的重要工具，幂函数的图象可以在单调性、奇偶性基础上较快描出．．师：教师用计算机作图y=x给学生展示标准

的图像，强调画图像易犯的错误．学生分小组画余下的4个幂函数，再填表格师：引导学生利用列表、描点、连线的方法画出函数的图像，用投影仪展示学生做的比较好的图像，和出错比较典型的图像.师：教师用计算机作图，给学生展示标准的图像，强调画图象易犯的

错误．y=x-3-xy=2xy=3xy=21xy=1−=xy定义域值域奇偶性单调性2、幂函数性质归纳（观察第一象限图象）性质：（1）所有的幂函数在（0，+∞）都有定义，并且图象都过点（1，1）；（2）如果α>0,则幂函数xy=在(0,+∞

)上为增函数，如果α<0,则幂函数xy=在(0,+∞)上为减函数观察第一象限图象，归纳幂函数一般性质师：引导学生根据总结的幂函数图像的一般规律师：引导学生探究归纳出所有幂函数的性质和图像的变化规律。多媒体演示5个幂函数在同一个坐标系的图像，引导学生归纳幂函

数一般性质例题：比较下列各题中两个值的大小：（1）8.02.5和8.03.5（2）525.2−和527.2−探究三、幂函数图象的变化规律探索一般幂函数xy=的图象随的变化规律。思考：幂函数在第一象限的图像有什么特点。幂函数在第一象限的

图像特点：直线X=1右侧，“指大图高”练一练：如图，比较1C、2C、3C、4C四个值的大小关系。讨论完成，个别自主回答运用幂函数的图像随的变师：引导学生根据总结的幂函数图像的一般规律，完成例题，幂函数的简单应用，利用到了幂函数的单调性引导学

生运用总结的幂函数图像的在第一象限图像随-4-课堂小结：提出1．谈谈本节课你学到了哪些数学知识？2．总结一下本节课我们用到了哪些数学思想方法？小结；两个内容：1.幂函数的定义2．幂函数的图像和性质两个思想;1.从特殊到一般的归纳思想2.数形结合的思想思考题：函数()()3221

−+−−=mmxmmxf是幂函数，且当()+,0x时，()xf是增函数，求()xf解析式作业：课时作业92页化规律解答自主小结：从定义及性质两方面进行总结的变化规律让学生总结自己的收获与不足.-5-板书设计幂函数一、定义二、幂

函数的图像和性质三、幂函数性质的应用教学反思幂函数作为一类重要的函数模型，是学生在系统学习了指数函数、对数函数之后研究的又一类基本初等函数。学生已经有了学习指数函数和对数函数的图象和性质的学习经历，幂函数概念的引入以及图象和性质的研究便水到渠成。其次学习一个新的函数，它

的图象至关重要，学生自己动手得出函数图象，是学生研究函数性质的基础。同时，也会给学生研究函数的提示。更好的体现数形结合思想在数学学习中的作用。本节课的设计，通过五个幂函数的图象和性质归纳出了一般幂函数的图象规律和性质，很好地遵循了特殊到一般的认

知规律，符合可接受性和可操作性原则，本能地把教学目标的落实融入到教学过程之中．贯彻新课程精神，根据学生实际情况和教师的自身特点，采用有针对性的教学策略，因材施教．教学中，通过引导学生动手实践、自主探索、合作交流，培养其良好的学习习惯，提高其动手绘图能力与创新意识，树立终身学

习的理念．本节课的创新之处在于用PPT动态演示五个幂函数的绘画过程，用几何画板验证学生得到的幂函数图像规律的正确性，提高学生学习的兴趣，体会研究数学的快乐。因此可认为：⒈达到基本的教学要求：通过五种特殊幂函数的性质和图像的研究，认识幂

函数的共同性质和图像变化规律，从而巩固对函数一般性质的认识。⒉通过观察图像得出幂函数的性质，体会数形结合的数学思想。⒊在教学过程中让同学自己动手绘图，训练学生基本功，引导学生自主探究。4.用几何画板作图，提高了学生学习的兴趣。在本节课的实践中，也有很多不足之处：比如引导学生自主探究还不够到位，时

间掌控不够好，板书也不够整洁，在以后的教学中，我一定注意改正。-6-