【文档说明】2024届高考一轮复习数学高考必刷题专练试题（新教材人教A版 提优版）第二章　必刷小题4　函数与方程 Word版.docx，共(4)页，162.847 KB，由小赞的店铺上传

转载请保留链接：https://www.doc5u.com/view-3870c3647a416006ae6f24f0bf14a001.html

以下为本文档部分文字说明：

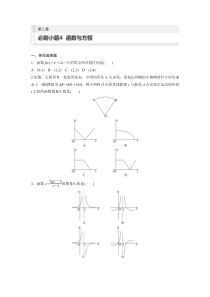
一、单项选择题1．函数f(x)＝ex＋2x－5的零点所在的区间是()A．(0,1)B．(1,2)C．(2,3)D．(3,4)2.如图，公园里有一处扇形花坛，小明同学从A点出发，沿花坛外侧的小路顺时针方向匀速走了一圈(路线为AB→BO→O

A)，则小明到O点的直线距离y与他从A点出发后运动的时间t之间的函数图象大致是()3．函数y＝lg|x－1|x－1的图象大致是()4．在使用二分法计算函数f(x)＝lgx＋x－2的零点的近似解时，现已知其所在区间为(1,2)，如果要求近似解的精确度为0.1，则接下来需

要计算________次区间中点的函数值()A．2B．3C．4D．55．信号在传输介质中传播时，将会有一部分能量转化为热能或被传输介质吸收，从而造成信号强度不断减弱，这种现象称为衰减．在试验环境下，超声波在某种介质的传播过程中，声压的衰减过程可以用指数模型

：P(s)＝P0e－Ks描述声压P(s)(单位：帕斯卡)随传播距离s(单位：米)的变化规律，其中P0为声压的初始值，常数K为试验参数．若试验中声压初始值为900帕斯卡，传播5米声压降低为400帕斯卡，据此可得试验参数K的估计值约为(参考数据：ln2

≈0.69，ln3≈1.10)()A．0.162B．0.164C．0.166D．0.1686．已知f(x)＝ln(－x)，x<0，2－x，x≥0，则函数y＝3f2(x)－2f(x)的零点个数为()A．1B．2C．3D．47．已知函数f(x)＝2x＋log2x

，且实数a>b>c>0，满足f(a)f(b)f(c)<0，若实数x0是函数y＝f(x)的一个零点，那么下列不等式中一定不成立的是()A．x0<aB．x0>aC．x0<bD．x0<c8．(2022·西安模拟)已知函数f(

x)＝f(x－2)，x>1，|x|－1，－1≤x≤1，若函数g(x)＝f(x)－loga(x＋1)恰有3个零点，则实数a的取值范围为()A.15，13B.15，13C.16，14D.

16，14二、多项选择题9．净水机通过分级过滤的方式使自来水逐步达到纯净水的标准，其中第一级过滤一般由孔径为5微米的PP棉滤芯(聚丙烯熔喷滤芯)构成，其结构是多层式，主要用于去除铁锈、泥沙、悬浮物等

各种大颗粒杂质．假设每一层PP棉滤芯可以过滤掉三分之一的大颗粒杂质，过滤前水中大颗粒杂质含量为50mg/L，若要满足过滤后水中大颗粒杂质含量不超过2.5mg/L，则PP棉滤芯层数不可能为()(参考数据：lg2≈0.30，lg3≈0.48

)A．5B．6C．7D．810．设函数f(x)＝x2＋2x，x≤0，lnx－x，x>0，则g(x)＝f(x)－m的零点个数可能是()A．1B．2C．3D．411.某医药研究机构开发了一种新药，据监测，如果患者每次按规定的剂量注

射该药物，注射后每毫升血液中的含药量y(微克)与时间t(小时)之间的关系近似满足如图所示的曲线．据进一步测定，当每毫升血液中含药量不少于0.125微克时，治疗该病有效，则()A．a＝3B．注射一次治疗该病的有效时间长度为6小时C．注射该药物18小

时后每毫升血液中的含药量为0.4微克D．注射一次治疗该病的有效时间长度为53132小时12．已知定义域为R的偶函数f(x)有4个零点x1，x2，x3，x4(x1<x2<x3<x4)，并且当x≥0时，f(x)＝x2－ax＋1，则下列说法中正确的是()A．实数

a的取值范围是(－∞，－2)∪(2，＋∞)B．当x<0时，f(x)＝x2＋ax＋1C．x1x2x3x4＝1D．x1＋2x2＋3x3＋4x4的取值范围是[23，＋∞)三、填空题13．为了预防信息泄露，保证

信息的安全传输，在传输过程中都需要对文件加密，有一种加密密钥密码系统(PrivateKeyCryptosystem)，其加密、解密原理为：发送方由明文→密文(加密)，接收方由密文→明文．现在加密密钥为y＝kx3，如“4”通过加密后得到

密文“2”，若接收方接到密文“1256”，则解密后得到的明文是________．14．若函数f(x)＝e－x－ln(x＋a)在(0，＋∞)上存在零点，则实数a的取值范围是________．15．已知函数y＝f(x)的表达式为f(x)＝x，x≤0，log2x，x>0

，则函数y＝f(f(x))的所有零点之和为________．16．渔民出海打鱼，为了保证获得的鱼新鲜，鱼被打上船后，要在最短的时间内将其分拣、冷藏，若不及时处理，打上来的鱼会很快失去新鲜度．已知某种鱼失去的新鲜度h与其出

水后时间t(分钟)满足的函数关系式为h＝m·at.若出水后10分钟，这种鱼失去的新鲜度为10%，出水后20分钟，这种鱼失去的新鲜度为20%，那么若不及时处理，打上来的这种鱼在________分钟后开始失去全部新鲜度．(已知lg2≈0.3，结果取整数)