【文档说明】十年（2015-2024）高考真题分项汇编 数学 专题21 立体几何大题综合 Word版含解析.docx，共(398)页，33.456 MB，由小赞的店铺上传

转载请保留链接：https://www.doc5u.com/view-0cd07329b252df4593f7881a54e21981.html

以下为本文档部分文字说明：

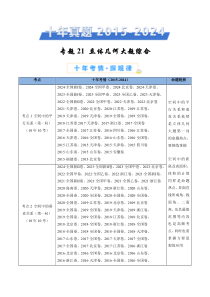
专题21立体几何大题综合考点十年考情（2015-2024）命题趋势考点1空间中的平行关系（第一问）（10年10考）2024·全国新Ⅰ卷、2024·全国甲卷、2024·北京卷、2024·天津卷、2023·全国新Ⅰ卷、2

023·全国甲卷、2023·全国乙卷、2023·天津卷、2022·全国新Ⅱ卷、2022·全国甲卷、2022·天津卷、2022·北京卷2021·天津卷、2020·北京卷、2020·江苏卷、2019·江苏卷、2019·天津卷、2019·天津卷、2019·全国卷、2

019·全国卷、2018·江苏卷2017·天津卷、2017·浙江卷、2017·全国卷2017·全国卷、2017·江苏卷、2016·四川卷、2016·江苏卷、2016·天津卷、2016·全国卷、2016·山东卷、2016·全国卷、2015·江苏

卷、2015·天津卷、2015·天津卷、2015·四川卷2015·山东卷、2015·山东卷、2015·安徽卷2015·福建卷、2015·北京卷空间中的平行关系和垂直关系依然是立体几何大题第一问的命题热点，要熟练掌握空间中的距离及表面积、体积的计

算同样是命题热点，异面直线所成角、线面角、二面角、及其最值范围等内容也是高频考点，同时也需掌握方程思想的应用考点2空间中的垂直关系（第一问）（10年10考）2024·全国新Ⅱ卷、2023·全国新Ⅱ卷、2023·全国甲卷、2023·北京卷、2022·全国甲卷、2022·全国乙

卷、2022·浙江卷、2021·全国新Ⅰ卷、2021·全国新Ⅱ卷、2021·全国甲卷、2021·全国乙卷、2021·浙江卷2020·海南卷、2020·天津卷、2020·浙江卷、2020·山东卷、2020·全国卷、2020·全国卷、2020·全国卷、2020·全国卷、2020·全国卷、2019·

江苏卷、2019·北京卷、2019·北京卷2019·全国卷、2019·全国卷、2019·天津卷、2019·浙江卷、2019·全国卷、2019·全国卷、2018·江苏卷、2018·北京卷、2018·北京卷、2018·全国卷、2018·浙江卷、2018·全国卷2018·全国卷、201

8·全国卷、2018·全国卷、2018·天津卷、2017·山东卷、2017·全国卷、2017·天津卷、2017·全国卷、2017·全国卷、2017·北京卷、2017·江苏卷、2016·浙江卷2016·北京卷、2016·全国卷、2016·北京卷、2016·山东卷

、2016·浙江卷、2016·天津卷、2016·全国卷、2016·全国卷、2015·广东卷、2015·江苏卷、2015·重庆卷、2015·重庆卷2015·浙江卷、2015·浙江卷、2015·全国卷、2015·全国卷、2015全国卷、2015·

天津卷、2015·陕西卷、2015·湖南卷、2015·湖南卷、2015·湖北卷、2015·福建卷、2015·北京卷2015·北京卷考点3求空间中的线段长度、点面距的值及最值或范围（10年6考）2024·全国甲卷、2024·天津卷、2023

·全国甲卷、2022·全国新Ⅰ卷、2021·全国乙卷、2019·全国卷、2018·全国卷考点4求空间中的体积、表面积的值及最值或范围（10年10考）2024·上海卷、2023·全国乙卷、2022·全国甲卷、2022·全国乙卷、2021·全国新Ⅰ卷、2021·

全国甲卷、2021·全国乙卷、2020·全国卷、2020·全国卷、2019·全国卷、2019·全国卷、2018·全国卷2017·上海卷、2017·全国卷、2017·北京卷、2017·全国卷、2016·江苏卷、2016·全国卷、2016·上海卷、2016·上海卷

、2016·全国卷、2016·全国卷、2015·重庆卷、2015·全国卷2015·湖南卷、2015·湖南卷、2015·湖北卷2015·福建卷、2015·北京卷考点5异面直线所成角及最值或范围（10年4考）2018·天

津卷、2017·天津卷、2016·上海卷、2015·广东卷、2015·全国卷、2015·上海卷、2015·山东卷考点6求线面角及最值或范围（10年10考）2024·天津卷、2024·上海卷、2023·全国甲

卷、2022·全国甲卷、2022·全国乙卷、2022·浙江卷、2022·天津卷、2021·浙江卷、2020·海南卷、2020·天津卷、2020·北京卷、2020·浙江卷2020·山东卷、2020·全国卷、2019·天津卷、2019·浙江

卷、2018·江苏卷、2018·浙江卷、2018·全国卷、2018·天津卷、2017·上海卷、2017·天津卷、2017·浙江卷、2017·北京卷2016·浙江卷、2016·天津卷、2016·全国卷、2016·北京卷、2016·天津卷

、2015·广东卷、2015·浙江卷、2015·天津卷、2015·上海卷、2015·全国卷考点7求二面角及最值或范围（10年10考）2024·全国新Ⅱ卷、2024·全国甲卷、2024·北京卷、2024·天津卷、202

3·全国新Ⅱ卷、2023·全国乙卷、2023·北京卷、2023·天津卷、2022·全国新Ⅰ卷、2022·全国新Ⅱ卷、2022·天津卷、2021·全国新Ⅱ卷2021·全国甲卷、2021·全国乙卷、2021·天津卷、2020·天津卷、2020·江苏卷、2020·全国卷、202

0·全国卷、2019·北京卷、2019·全国卷、2019·全国卷、2019·全国卷、2018·北京卷2018·全国卷、2017·山东卷、2017·全国卷、2016·天津卷、2016·山东卷、2016·浙江卷、2016·全国卷、2016·全国卷、2015·广东卷、2015·重庆卷

、2015·浙江卷、2015·四川卷2015·陕西卷、2015·山东卷、2015·安徽卷2015·福建卷、2015·北京卷考点8已知异面直线所成角、线面角、二面角求值或范围（方程思想）（10年5考）2024·全国新Ⅰ卷、2023·全国新Ⅰ卷、2021·全国新Ⅰ卷、20

21·北京卷、2017·天津卷、2017·全国卷、2015·天津卷、2015·湖南卷、2015·湖南卷、2015·湖北卷考点01空间中的平行关系（第一问）1．（2024·全国新Ⅰ卷·高考真题）如图，四棱锥P

ABCD−中，PA⊥底面ABCD，2PAAC==，1,3BCAB==．(1)若ADPB⊥，证明：//AD平面PBC；【答案】(1)证明见解析【分析】（1）先证出AD⊥平面PAB，即可得ADAB⊥，由勾股定理逆定理可得BCA

B⊥，从而//ADBC，再根据线面平行的判定定理即可证出；【详解】（1）（1）因为PA⊥平面ABCD，而AD平面ABCD，所以PAAD⊥，又ADPB⊥，PBPAP=，,PBPA平面PAB，所以AD⊥平

面PAB，而AB平面PAB，所以ADAB⊥.因为222BCABAC+=，所以BCAB⊥，根据平面知识可知//ADBC，又AD平面PBC，BC平面PBC，所以//AD平面PBC．2．（2024·全国甲卷·高考真题）如图，在以

A，B，C，D，E，F为顶点的五面体中，四边形ABCD与四边形ADEF均为等腰梯形，//,//EFADBCAD，4,2ADABBCEF====，10,23EDFB==，M为AD的中点．(1)证明：//BM平面CDE；【答案】(1)证明见详解；【分析】（1）结合已知易证四边形BCDM为平行

四边形，可证//BMCD，进而得证；【详解】（1）因为//,2,4,BCADEFADM==为AD的中点，所以//,BCMDBCMD=，四边形BCDM为平行四边形，所以//BMCD，又因为BM平面CDE，CD平面CDE，所以//BM平面CDE；3．（2024·北京·高考真题）如图，在四棱

锥PABCD−中，//BCAD，1ABBC==，3AD=,点E在AD上，且PEAD⊥，2PEDE==．(1)若F为线段PE中点，求证：//BF平面PCD．【答案】(1)证明见解析【分析】（1）取PD的中点为S，接,SFSC，可证四边形SFBC为平行四边形，由线面平

行的判定定理可得//BF平面PCD.【详解】（1）取PD的中点为S，接,SFSC，则1//,12SFEDSFED==，而//,2EDBCEDBC=，故//,SFBCSFBC=，故四边形SFBC为平行四边形，故//BFSC，而

BF平面PCD，SC平面PCD，所以//BF平面PCD.4．（2024·天津·高考真题）已知四棱柱1111ABCDABCD−中，底面ABCD为梯形，//ABCD，1AA⊥平面ABCD，ADAB⊥，其中12,1ABAAADDC====．N是11BC的中点，M是1DD的中点．(1)求证1//D

N平面1CBM；【答案】(1)证明见解析【分析】（1）取1CB中点P，连接NP，MP，借助中位线的性质与平行四边形性质定理可得1N//DMP，结合线面平行判定定理即可得证；【详解】（1）取1CB中点P

，连接NP，MP，由N是11BC的中点，故1//NPCC，且112NPCC=，由M是1DD的中点，故1111122DMDDCC==，且11//DMCC，则有1//DMNP、1DMNP=，故四边形1DMPN是平行四边形，故1//DNMP，又MP平面1CBM，1DN平面1CBM，故1//DN平面1

CBM；5．（2023·全国新Ⅰ卷·高考真题）如图，在正四棱柱1111ABCDABCD−中，12,4ABAA==．点2222,,,ABCD分别在棱111,,AABBCC,1DD上，22221,2,3AABBDD

CC====．(1)证明：2222BCAD∥；【答案】(1)证明见解析；【分析】（1）建立空间直角坐标系，利用向量坐标相等证明；【详解】（1）以C为坐标原点，1,,CDCBCC所在直线为,,xyz轴建立空间直角坐标系，如图，则2222(0,0,0),(0,0,3),(

0,2,2),(2,0,2),(2,2,1)CCBDA，2222(0,2,1),(0,2,1)BCAD=−=−，2222BCAD∥，又2222BCAD，不在同一条直线上，2222BCAD∥.6．（2023·全国甲卷·高考真题）如图，在三棱锥−PABC中，ABBC⊥，2AB=，22BC=，6

PBPC==，BP，AP，BC的中点分别为D，E，O，5ADDO=，点F在AC上，BFAO⊥.(1)证明：//EF平面ADO；【答案】(1)证明见解析；【分析】（1）根据给定条件，证明四边形ODEF为平行

四边形，再利用线面平行的判定推理作答.【详解】（1）连接,DEOF，设AFtAC=，则(1)BFBAAFtBAtBC=+=−+，12AOBABC=−+，BFAO⊥，则2211[(1)]()(1)4(1)4022BFAOtBAtBCBABCtBAtBCtt=−+−+=−+=−+=，解得12t=

，则F为AC的中点，由,,,DEOF分别为,,,PBPABCAC的中点，于是11//,,//,22DEABDEABOFABOFAB==，即,//DEOFDEOF=，则四边形ODEF为平行四边形，//,EFDOEFDO=，又EF平面,ADODO平面ADO，所以//EF平面AD

O.7．（2023·全国乙卷·高考真题）如图，在三棱锥−PABC中，ABBC⊥，2AB=，22BC=，6PBPC==，,,BPAPBC的中点分别为,,DEO，点F在AC上，BFAO⊥．(1)求证：EF//平面ADO；【答案】(1)证明见解析【分析】（1）根据给定条件，证明四边形ODEF为平行四边形

，再利用线面平行的判定推理作答.【详解】（1）连接,DEOF，设AFtAC=，则(1)BFBAAFtBAtBC=+=−+，12AOBABC=−+，BFAO⊥，则2211[(1)]()(1)4(1)4022BFAOtBAtBC

BABCtBAtBCtt=−+−+=−+=−+=，解得12t=，则F为AC的中点，由,,,DEOF分别为,,,PBPABCAC的中点，于是11//,,//,22DEABDEABOFABOFAB==，即,//DEOFDEOF=，

则四边形ODEF为平行四边形，//,EFDOEFDO=，又EF平面,ADODO平面ADO，所以//EF平面ADO.8．（2023·天津·高考真题）如图，在三棱台111ABCABC-中，1AA⊥平面111,,2,1ABCABACABACA

AAC⊥====，M为BC中点.，N为AB的中点，(1)求证：1AN//平面1AMC；【答案】(1)证明见解析【分析】（1）先证明四边形11MNAC是平行四边形，然后用线面平行的判定解决；【详解】（1）连接1,MNCA.由

,MN分别是,BCBA的中点，根据中位线性质，MN//AC，且12ACMN==，由棱台性质，11AC//AC，于是MN//11AC，由111MNAC==可知，四边形11MNAC是平行四边形，则1AN//1MC，又1AN平面1CMA，

1MC平面1CMA，于是1AN//平面1AMC.9．（2022·全国新Ⅱ卷·高考真题）如图，PO是三棱锥−PABC的高，PAPB=，ABAC⊥，E是PB的中点．(1)证明：//OE平面PAC；【答案】(1)证明见解析【分析】（1）连接BO并延长交AC于点D，连接OA、PD，根据三角形全等

得到OAOB=，再根据直角三角形的性质得到AODO=，即可得到O为BD的中点从而得到//OEPD，即可得证；【详解】（1）证明：连接BO并延长交AC于点D，连接OA、PD，因为PO是三棱锥−PABC的高，所以PO⊥平面ABC，,AOBO平面ABC，所以POAO⊥、POBO⊥，又PAPB=

，所以POAPOB△△，即OAOB=，所以OABOBA=，又ABAC⊥，即90BAC=，所以90OABOAD+=，90OBAODA+=，所以ODAOAD=所以AODO=，即AODOOB==，所以O为BD的中点，又E为

PB的中点，所以//OEPD，又OE平面PAC，PD平面PAC，所以//OE平面PAC10．（2022·全国甲卷·高考真题）小明同学参加综合实践活动，设计了一个封闭的包装盒，包装盒如图所示：底面ABCD是边长为8（单位：cm）的正方形，,,,

EABFBCGCDHDA均为正三角形，且它们所在的平面都与平面ABCD垂直．(1)证明：//EF平面ABCD；【答案】(1)证明见解析；【分析】（1）分别取,ABBC的中点,MN，连接MN，由平面知识可知,EMABFNBC⊥⊥，EMFN=，依题从而可证EM⊥平面

ABCD，FN⊥平面ABCD，根据线面垂直的性质定理可知//EMFN，即可知四边形EMNF为平行四边形，于是//EFMN，最后根据线面平行的判定定理即可证出；【详解】（1）如图所示：分别取,ABBC的中点,MN，连

接MN，因为,EABFBC为全等的正三角形，所以,EMABFNBC⊥⊥，EMFN=，又平面EAB⊥平面ABCD，平面EAB平面ABCDAB=，EM平面EAB，所以EM⊥平面ABCD，同理可得FN⊥平面ABCD，根据线面垂直的性质定理可知//EMFN，而EMFN=，所以四边形EMNF为平行

四边形，所以//EFMN，又EF平面ABCD，MN平面ABCD，所以//EF平面ABCD．11．（2022·天津·高考真题）直三棱柱111ABCABC-中，112,,AAABACAAABACAB===⊥⊥，D为11AB的中点，E为1AA的中点，F为CD

的中点．(1)求证：//EF平面ABC；【答案】(1)证明见解析【分析】（1）以点1A为坐标原点，1AA、11AB、11AC所在直线分别为x、y、z轴建立空间直角坐标系，利用空间向量法可证得结论成立；【详解】（1）证明：在直三棱柱111ABCABC-中，1AA⊥平面111ABC，且A

CAB⊥，则1111ACAB⊥以点1A为坐标原点，1AA、11AB、11AC所在直线分别为x、y、z轴建立如下图所示的空间直角坐标系，则()2,0,0A、()2,2,0B、()2,0,2C、()10,0,0A、()1

0,2,0B、()10,0,2C、()0,1,0D、()1,0,0E、11,,12F，则10,,12EF=，易知平面ABC的一个法向量为()1,0,0m=，则0EFm=，故EFm⊥，EF

平面ABC，故//EF平面ABC.12．（2022·北京·高考真题）如图，在三棱柱111ABCABC-中，侧面11BCCB为正方形，平面11BCCB⊥平面11ABBA，2ABBC==，M，N分别为11AB，AC的中点．(1)求证：MN∥平面11BCCB；【答案】(1)

见解析【分析】（1）取AB的中点为K，连接,MKNK，可证平面//MKN平面11BCCB，从而可证//MN平面11BCCB.【详解】（1）取AB的中点为K，连接,MKNK，由三棱柱111ABCABC-可得四边形11ABBA为平行四边形，而11,

BMMABKKA==，则1//MKBB，而MK平面11BCCB，1BB平面11BCCB，故//MK平面11BCCB，而,CNNABKKA==，则//NKBC，同理可得//NK平面11BCCB，而,,NKMKKNKMK=平面MKN，故平面//MKN平面11BCCB，而MN平面MK

N，故//MN平面11BCCB，13．（2021·天津·高考真题）如图，在棱长为2的正方体1111ABCDABCD−中，E为棱BC的中点，F为棱CD的中点．（I）求证：1//DF平面11AEC；【答案】（I）证明见解析；（II）39；（III）13.【

分析】（I）建立空间直角坐标系，求出1DF及平面11AEC的一个法向量m，证明1mDF⊥，即可得证；【详解】（I）以A为原点，1,,ABADAA分别为,,xyz轴，建立如图空间直角坐标系，则()0,0,0A,()10

,0,2A,()2,0,0B,()2,2,0C,()0,2,0D,()12,2,2C,()10,2,2D，因为E为棱BC的中点，F为棱CD的中点，所以()2,1,0E，()1,2,0F，所以()11,0,2DF=−,()112,2,0AC

=,()12,1,2AE=−,设平面11AEC的一个法向量为()111,,mxyz=，则11111111202202mxymxyAAEzC+=+−===，令12x=，则()2,2,1m=−，因为1220mDF=−=，所以1mDF⊥，因为1DF平面11AEC，所以

1//DF平面11AEC；14．（2020·北京·高考真题）如图，在正方体1111ABCDABCD−中，E为1BB的中点．（Ⅰ）求证：1//BC平面1ADE；【答案】（Ⅰ）证明见解析；（Ⅱ）23.【分析】（Ⅰ）证明出四边形11ABCD为平行四边形，可得出11//BCAD，然后利用线面平行的判定

定理可证得结论；也可利用空间向量计算证明；【详解】（Ⅰ）[方法一]：几何法如下图所示：在正方体1111ABCDABCD−中，11//ABAB且11ABAB=，1111//ABCD且1111ABCD=，11//ABCD且11ABCD=，所以，四边形11ABCD为平行四边形，则11//BCAD，

1BC平面1ADE，1AD平面1ADE，1//BC平面1ADE；[方法二]:空间向量坐标法以点A为坐标原点，AD、AB、1AA所在直线分别为x、y、z轴建立如下图所示的空间直角坐标系Axyz−，设正方体1111ABCDAB

CD−的棱长为2，则()0,0,0A、()10,0,2A、()12,0,2D、()0,2,1E，()12,0,2AD=，()0,2,1AE=，设平面1ADE的法向量为(),,nxyz=，由100nADnAE==

，得22020xzyz+=+=，令2z=−，则2x=，1y=，则()2,1,2n=−.又∵向量()12,0,2BC=,()1·2201220BCn=++−=,又1BC平面1ADE，1//BC平面1ADE；15．（2

020·江苏·高考真题）在三棱柱ABC-A1B1C1中，AB⊥AC，B1C⊥平面ABC，E，F分别是AC，B1C的中点．（1）求证：EF∥平面AB1C1；【答案】（1）证明详见解析；【分析】（1）通过证明1

//EFAB，来证得//EF平面11ABC.【详解】（1）由于,EF分别是1,ACBC的中点，所以1//EFAB.由于EF平面11ABC,1AB平面11ABC，所以//EF平面11ABC.16．（2019·江苏·高考真题

）如图，在直三棱柱ABC－A1B1C1中，D，E分别为BC，AC的中点，AB=BC．求证：（1）A1B1∥平面DEC1；【答案】（1）见解析；【分析】(1)由题意结合几何体的空间结构特征和线面平行的判定定理即可证得题中的结论；【详解】（1）因为D，E分别为BC，AC的中点，所

以ED∥AB.在直三棱柱ABC-A1B1C1中，AB∥A1B1，所以A1B1∥ED.又因为ED⊂平面DEC1，A1B1平面DEC1，所以A1B1∥平面DEC1.17．（2019·天津·高考真题）如图，在四棱锥PABCD−中，底面AB

CD为平行四边形，PCD为等边三角形，平面PAC⊥平面PCD，PACD⊥，2CD=，3AD=，（Ⅰ）设GH，分别为PBAC，的中点，求证：GH平面PAD；【答案】（I）见解析；【分析】（I）连接BD，结合平行四边形的性质，以及三角形中位线的性质，得到GHPD，利用线面平行的判定定理

证得结果；【详解】（I）证明：连接BD，易知ACBDH=，BHDH=，又由BG=PG，故GHPD，又因为GH平面PAD，PD平面PAD，所以GH平面PAD.18．（2019·天津·高考真题）如图，⊥AE平面ABCD，,CFAEADBC∥∥，,1,2ADABABADAEBC⊥====.（Ⅰ

）求证：BF∥平面ADE；【答案】（Ⅰ）见证明；【分析】首先利用几何体的特征建立空间直角坐标系(Ⅰ)利用直线BF的方向向量和平面ADE的法向量的关系即可证明线面平行；【详解】依题意，可以建立以A为原点，分别以,,ABADAE的方向为x轴，y轴，z轴正方向的

空间直角坐标系(如图)，可得()()()()()0,0,0,1,0,0,1,2,0,0,1,0,0,0,2ABCDE.设()0CFhh=，则()1,2,Fh.(Ⅰ)依题意，()1,0,0AB=是平面ADE的法向量，又()0,2,BFh=，可得0BFAB=，又因为直线BF平面AD

E，所以BF平面ADE.19．（2019·全国·高考真题）如图，直四棱柱ABCD–A1B1C1D1的底面是菱形，AA1=4，AB=2，∠BAD=60°，E，M，N分别是BC，BB1，A1D的中点.（1）证明：

MN∥平面C1DE；【答案】（1）见解析；【分析】（1）利用三角形中位线和11//ADBC可证得//MEND，证得四边形MNDE为平行四边形，进而证得//MNDE，根据线面平行判定定理可证得结论；【详解】

（1）连接ME，1BCM，E分别为1BB，BC中点ME为1BBC的中位线1//MEBC且112MEBC=又N为1AD中点，且11//ADBC1//NDBC且112NDBC=//MEND四边形MNDE为平行四边形//MNDE，又MN平面1CDE，DE平面1CD

E//MN平面1CDE20．（2019·全国·高考真题）如图，直四棱柱ABCD–A1B1C1D1的底面是菱形，AA1=4，AB=2，∠BAD=60°，E，M，N分别是BC，BB1，A1D的中点．（1）证明：MN∥平面C1DE；【答案】（1）见解析；【分析

】（1）利用三角形中位线和11//ADBC可证得//MEND，证得四边形MNDE为平行四边形，进而证得//MNDE，根据线面平行判定定理可证得结论；【详解】（1）连接ME，1BCM，E分别为1BB，BC中点ME为1BBC的中位线1

//MEBC且112MEBC=又N为1AD中点，且11//ADBC1//NDBC且112NDBC=//MEND四边形MNDE为平行四边形//MNDE，又MN平面1CDE，DE平面1CDE//MN平面1CDE21．（2018·江苏·高考真题）在平行六

面体1111ABCDABCD−中，1AAAB=,111ABBC⊥．求证：（1）11//ABABC平面；【答案】（1）见解析【详解】分析：（1）先根据平行六面体得线线平行，再根据线面平行判定定理得结论；证明：（1）在平行六面体ABCD-A1B1C1D1中，AB∥A1B1．因

为AB平面A1B1C，A1B1平面A1B1C，所以AB∥平面A1B1C．22．（2017·天津·高考真题）如图，在三棱锥−PABC中，PA⊥底面ABC，90BAC=．点D，E，N分别为棱PA，PC，BC的中

点，M是线段AD的中点，4PAAC==，2AB=．（1）求证：MN∥平面BDE；【答案】（1）证明见解析；试题解析：如图，以A为原点，分别以AB，AC，AP方向为x轴、y轴、z轴正方向建立空间直角坐标系.依题意可得A（0，0，0），B

（2，0，0），C（0，4，0），P（0，0，4），D（0，0，2），E（0，2，2），M（0，0，1），N（1，2，0）.（1）证明：DE=（0，2，0），DB=（2，0，2−）.设(),,nxyz=，为平面BDE的法向量，则00nDE

nDB==，即20220yxz=−=.不妨设1z=，可得()1,0,1n=.又MN=（1，2，1−），可得0MNn=.因为MN平面BDE，所以MN//平面BDE.23．（2017·浙江·高考真题）如图，已知四棱锥P-ABCD，△PAD是以AD为斜边的等腰直角三角形，

BC∥AD，CD⊥AD，PC=AD=2DC=2CB,E为PD的中点.（I）证明：CE∥平面PAB；【答案】（I）见解析；试题解析：（Ⅰ）如图，设PA中点为F，连接EF，FB．因为E，F分别为PD，PA中点，所以//EFAD且12

EFAD=，又因为//BCAD，12BCAD=，所以//EFBC且EFBC=，即四边形BCEF为平行四边形，所以//CEBF，因此//CE平面PAB．24．（2017·全国·高考真题）如图，四棱锥P-ABCD中，侧面PAD是边长为2的等边三角形且垂直于底面ABCD，o1,90,2ABBCAD

BADABC====E是PD的中点．（1）证明：直线//CE平面PAB；【答案】（1）见解析；【详解】试题分析：（1）取PA的中点F，连结EF，BF，由题意证得CE∥BF，利用线面平行的判断定理即可证得结论；试题解析：（1）取PA中点F，连结EF，BF．因为E为PD的中点，所

以//EFAD,12EFAD=,由90BADABC==得//BCAD，又12BCAD=所以．四边形BCEF为平行四边形，//CEBF．又BFPAB平面，CEPAB平面，故//CEPAB平面25．（2017·全国·高考真题）四棱锥

PABCD−中，侧面PAD为等边三角形且垂直于底面ABCD,01,90.2ABBCADBADABC====（1）证明：直线//BC平面PAD;【答案】（Ⅰ）见解析试题解析：（1）在平面内，因为,所以又平面平面故平面26．（2017·江苏·高考真题）如图，在三棱锥A­BCD中，AB⊥A

D，BC⊥BD，平面ABD⊥平面BCD，点E，F(E与A，D不重合)分别在棱AD，BD上，且EF⊥AD.求证：(1)EF∥平面ABC；【答案】（1）见解析【详解】试题分析：（1）先由平面几何知识证明EFAB∥，再由线面平行判定定理得结论；试题解析：证明：（1）在平面ABD内，因为AB⊥AD，EF

AD⊥，所以EFAB.又因为EF平面ABC，AB平面ABC，所以EF∥平面ABC.27．（2016·四川·高考真题）如图，在四棱锥P-ABCD中，PA⊥CD，AD∥BC，∠ADC=∠PAB=90°，BC=CD=12AD．（Ⅰ）在平面PAD内找一点M

，使得直线CM∥平面PAB，并说明理由；【答案】（Ⅰ）详见解析；（Ⅰ）取棱AD的中点M（M∈平面PAD），点M即为所求的一个点.理由如下：因为AD∥BC,BC=12AD，所以BC∥AM,且BC=AM.所以四边形AMCB是平行四边形，从而CM∥AB.又

AB平面PAB,CM平面PAB,所以CM∥平面PAB.（说明：取棱PD的中点N,则所找的点可以是直线MN上任意一点）28．（2016·江苏·高考真题）如图，在直三棱柱ABC-A1B1C1中，D，E分别为AB

，BC的中点，点F在侧棱B1B上，且11BDAF⊥，1111ACAB⊥.求证：（1）直线DE平面A1C1F；【答案】（1）详见解析试题解析：证明：（1）在直三棱柱111ABCABC-中，11ACAC，在三角形ABC中，因为D，E分别为AB，BC的中点，所以DEAC，于是11DEAC，又因

为DE平面1111,ACFAC平面11ACF，所以直线DE//平面11ACF.29．（2016·天津·高考真题）如图，正方形ABCD的中心为O，四边形OBEF为矩形，平面OBEF⊥平面ABCD，点G为AB的中点，AB=BE=2.（Ⅰ）求证：E

G∥平面ADF；【答案】（Ⅰ）详见解析；试题解析：依题意，OFABCD⊥平面，如图，以O为点，分别以,,ADBAOF的方向为x轴、y轴、z轴的正方向建立空间直角坐标系，依题意可得(0,0,0)O，()1,1,0,(1,1,0

),(1,1,0),(11,0),(1,1,2),(0,0,2),(1,0,0)ABCDEFG−−−−−−−，.（Ⅰ）证明：依题意，()(2,0,0),1,1,2ADAF==−.设()1,,nxyz=为平面ADF的法向量，则110{0nADnAF==，即2

0{20xxyz=−+=.不妨设1z=，可得()102,1n=,，又()0,1,2EG=−，可得10EGn=，又因为直线EGADF平面，所以//EGADF平面.30．（2016·全国·高考真题）如图，四棱锥P−ABCD中，PA⊥底面ABCD，AD∥BC，AB

=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，N为PC的中点.（Ⅰ）证明MN∥平面PAB;【答案】（Ⅰ）详见解析；【详解】（Ⅰ）由已知得223AMAD==.取BP的中点T，连接,A

TTN，由N为PC中点知TN//BC，122TNBC==.又//ADBC，故//TNAM，TNAM=，四边形AMNT为平行四边形，于是MNAT.因为AT平面PAB，MN平面PAB，所以//MN平面PAB.31．（2016·

山东·高考真题）在如图所示的圆台中，AC是下底面圆O的直径，EF是上底面圆O'的直径，FB是圆台的一条母线.（Ⅰ）已知G,H分别为EC，FB的中点，求证：GH∥平面ABC；【答案】（Ⅰ）见解析；【详解】(Ⅰ)连结FC，取FC的中点M，连结G

M，HM，//GMEF、EF在上底面内，GM不在上底面内，//GM上底面，//GM平面ABC，又MH//BC，BC平面ABC，MH平面ABC，H//M平面ABC，所以平面GHM//平面ABC，由G

H平面GHM，GH//平面ABC．32．（2016·全国·高考真题）如图，四棱锥PABCD−中，PA⊥平面ABCD，ADBC∥，3ABADAC===，4PABC==，M为线段AD上一点，2AMMD=，N为PC的中点．（I

）证明MN∥平面PAB；【答案】(Ⅰ)证明见解析；试题解析：（Ⅰ）由已知得，取的中点T，连接，由N为中点知，.又，故平行且等于，四边形AMNT为平行四边形，于是.因为平面，平面，所以平面.33．（2015·江苏·高考真

题）如图，在直三棱柱中，已知，，设的中点为，.求证：（1）；【答案】（1）详见解析试题解析：（1）由题意知，为1C的中点，又D为1的中点，因此D//C．又因为D平面11CC，C平面11

CC，所以D//平面11CC．34．（2015·天津·高考真题）如图,已知1AA⊥平面ABC,AB=AC=3,,,点E,F分别是BC,11AB的中点.（Ⅰ）求证:EF∥平面;【答案】（Ⅰ）见试题解析;试题解析:（Ⅰ）证明:如图,连接1AC,在△1BCB中,因为E和

F分别是BC,1BB的中点,所以11ABN,又因为EF平面11ABBA,所以EF∥平面11ABBA.35．（2015·天津·高考真题）如图，在四棱柱1111ABCDABCD−中，侧棱1AA⊥底面ABCD，ABA

C⊥，1AB=，12ACAA==，5ADCD==，且点M和N分别为1BC和1DD的中点.（1）求证：//MN平面ABCD；【答案】（1）证明见解析；【详解】如图，以A为原点建立空间直角坐标系，依题意可得(0,0,0),(0,1,0),(2,0,0),(1,2,0

)ABCD−，又因为,MN分别为1BC和1DD的中点，得11,,1,(1,2,1)2MN−.（Ⅰ）证明：依题意，可得(0,0,1)n=为平面ABCD的一个法向量，50,,02MN=−

，由此可得，0MNn=，又因为直线MN平面ABCD，所以//MN平面ABCD36．（2015·四川·高考真题）一个正方体的平面展开图及该正方体的直观图的示意图如图所示，在正方体中，设BC的中点为M，GH的中点为N(

1)请将字母,,FGH标记在正方体相应的顶点处（不需说明理由）(2)证明：直线//MN平面BDH【详解】（1）点F、G、H的位置如图所示.（2）连结BD，设O为BD的中点.因为M、N分别是BC、GH的中点，所以//NHCD，且12NHCD=，

//MNOH，且12NHCD=，所以//,OMNHOMNH=，所以PKM是平行四边形，从而MPAC⊥，又OH平面BDH，//MN平面BDH，MN平面BDH，所以//MN平面BDH.37．（2015·山东·高考真题）如图，三棱台DEFABC−中，2ABDEGH=，，分别为ACBC，

的中点.（Ⅰ）求证：//BD平面FGH；【详解】（Ⅰ）证法一：连接,.DGCD设CDGFM=,连接MH，在三棱台DEFABC−中，2ABDEG=，分别为AC的中点，可得//,DFGCDFGC=，所以四边形DFCG是平行四边形，则M为CD的中点，又H是BC的中点，所以//HMBD,又H

M平面FGH，BD平面FGH，所以//BD平面FGH.证法二：在三棱台DEFABC−中，由2,=BCEFH为BC的中点，可得//,,BHEFBHEF=所以HBEF为平行四边形，可得//.BEHF在ABC中，GH，分别为ACBC，的中点，所以//,GHAB又GHHFH=，所以平面/

/FGH平面ABED，因为BD平面ABED，所以//BD平面FGH.38．（2015·山东·高考真题）如图，在三棱台DEFABC−中，2,,ABDEGH=分别为,ACBC的中点．（Ⅰ）求证：//BD平面FGH；试题解析：（Ⅰ）证法一：连接,DGCD，设CDGFO=，连接OH，在

三棱台DEFABC−中，2,ABDEG=为AC的中点可得//,DFGCDFGC=所以四边形DFCG为平行四边形则O为CD的中点又H为BC的中点所以//OHBD又OH平面,FGHBD平面,FGH所以//BD平面FGH．

证法二：在三棱台DEFABC−中，由2,=BCEFH为BC的中点可得//,,BHEFBHEF=所以四边形BHFE为平行四边形可得//BEHF在ABC中，G为AC的中点，H为BC的中点，所以//GHAB又GHHFH=，所以平面//FGH平面ABED因为BD平面ABE

D所以//BD平面FGH39．（2015·安徽·高考真题）如图所示，在多面体111ABDDCBA，四边形11AABB，11,ADDAABCD均为正方形，E为11BD的中点，过1,,ADE的平面交1CD于

F.（Ⅰ）证明：1//EFBC；【答案】（Ⅰ）1//EFBC；试题解析：（Ⅰ）证明：由正方形的性质可知11////ABABDC，且11ABABDC==，所以四边形11ABCD为平行四边形，从而11//BCAD，又1AD面1ADE，1BC面1ADE，于是1//BC面1ADE，又1BC

面11BCD，而面1ADE面11BCDEF=，所以1//EFBC.40．（2015·福建·高考真题）如图，在几何体ABCDE中，四边形ABCD是矩形，AB⊥平面BEC，BEEC⊥，ABBEEC==，G，F分别是线段BE，DC的中点.(1)求证：//GF平面ADE；【详解】（1）如图，取AE的中点H

连接HG，HD，又G是BE的中点，所以//HGAB，且12HGAB=，又F是CD中点，所以12DFCD=，由四边形ABCD是矩形得，//ABCD，ABCD=，所以//GHDF且GHDF=.从而四边形HGFD是平行四边形，所以//GFDH，∵DH平面ADE，G

F平面ADE，∴//GF平面ADE.41．（2015·北京·高考真题）如图，在三棱锥VC−中，平面V⊥平面C，V为等边三角形，CC⊥且CC2==，，分别为，V的中点．(1)求证：V//平面C；试题

解析：（Ⅰ）证明：∵O，M分别为AB，VA的中点，∴OM∥VB，∵VB⊄平面MOC，OM⊂平面MOC，∴VB∥平面MOC；考点02空间中的垂直关系（第一问）1．（2024·全国新Ⅱ卷·高考真题）如图，平面四边形ABCD中，8AB=，3CD=，53AD=，90ADC=

，30BAD=，点E，F满足25AEAD=，12AFAB=，将AEF△沿EF翻折至PEF!，使得43PC=．(1)证明：EFPD⊥；(2)求平面PCD与平面PBF所成的二面角的正弦值．【答案】(1)证明见解析(2)

86565【分析】（1）由题意，根据余弦定理求得2EF=，利用勾股定理的逆定理可证得EFAD⊥，则,EFPEEFDE⊥⊥，结合线面垂直的判定定理与性质即可证明；（2）由（1），根据线面垂直的判定定理与性质可证明PEED⊥，建立如图空间直角坐标系Exyz−，利

用空间向量法求解面面角即可.【详解】（1）由218,53,,52ABADAEADAFAB====，得23,4AEAF==，又30BAD=，在AEF△中，由余弦定理得2232cos1612242322EFAEAF

AEAFBAD=+−=+−=,所以222AEEFAF+=，则AEEF⊥，即EFAD⊥，所以,EFPEEFDE⊥⊥，又,PEDEEPEDE=、平面PDE，所以EF⊥平面PDE，又PD平面PDE，故EF⊥PD；（2）连

接CE，由90,33,3ADCEDCD===，则22236CEEDCD=+=，在PEC中，43,23,6PCPEEC===，得222ECPEPC+=，所以PEEC⊥，由（1）知PEEF⊥，又,ECE

FEECEF=、平面ABCD，所以PE⊥平面ABCD，又ED平面ABCD，所以PEED⊥，则,,PEEFED两两垂直，建立如图空间直角坐标系Exyz−，则(0,0,0),(0,0,23),(0,33,0),(3,33,0),(2,0,0),(0,23,0)EPDCFA−

，由F是AB的中点，得(4,23,0)B，所以(3,33,23),(0,33,23),(4,23,23),(2,0,23)PCPDPBPF=−=−=−=−，设平面PCD和平面PBF的一个法向量分别为111222(,,),(,,)nxyzmxy

z==，则1111133323033230nPCxyznPDyz=+−==−=，222224232302230mPBxyzmPFxz=+−==−=，令122,3yx==，得11220,3,1,1xzyz===−=，所以(0,2,3),(3,1,1

)nm==−，所以165cos,65513mnmnmn===，设平面PCD和平面PBF所成角为，则2865sin1cos65=−=，即平面PCD和平面PBF所成角的正弦值为86565.2．（2023·全国新Ⅱ卷·高考真题）如图，三棱锥ABCD−中

，DADBDC==，BDCD⊥，60ADBADC==，E为BC的中点．(1)证明：BCDA⊥；(2)点F满足EFDA=，求二面角DABF−−的正弦值．【答案】(1)证明见解析；(2)33．【分析】（1）根据题意易证BC⊥平面ADE，从而证得BCDA⊥；（2）由题可证⊥AE平面

BCD，所以以点E为原点，,,EDEBEA所在直线分别为,,xyz轴，建立空间直角坐标系，再求出平面,ABDABF的一个法向量，根据二面角的向量公式以及同角三角函数关系即可解出．【详解】（1）连接,AEDE，因为E为BC中点，DBDC=，所以DEBC⊥①，因为DADBDC==，60AD

BADC==，所以ACD与ABD△均为等边三角形，ACAB=，从而AEBC⊥②，由①②，AEDEE=，,AEDE平面ADE，所以，BC⊥平面ADE，而AD平面ADE，所以BCDA⊥．（2）不妨设2DAD

BDC===，BDCD⊥，22,2BCDEAE===．2224AEDEAD+==，AEDE⊥，又,AEBCDEBCE⊥=，,DEBC平面BCDAE⊥平面BCD．以点E为原点，,,EDEBEA所在直线分别为,,xyz轴，建立空间直

角坐标系，如图所示：设(2,0,0),(0,0,2),(0,2,0),(0,0,0)DABE，设平面DAB与平面ABF的一个法向量分别为()()11112222,,,,,nxyznxyz==，二面角D

ABF−−平面角为,而()0,2,2AB=−，因为()2,0,2EFDA==−，所以()2,0,2F−，即有()2,0,0AF=−，1111220220xzyz−+=−=，取11x=，所以1(1,1,1)n=；22222020yzx−=−=

，取21y=，所以2(0,1,1)n=，所以，121226cos332nnnn===，从而63sin193=−=．所以二面角DABF−−的正弦值为33．3．（2023·全国甲卷·高考真题）如图，在三棱柱111ABCABC-中，1AC⊥平面,90ABCACB=

．(1)证明：平面11ACCA⊥平面11BBCC；(2)设11,2ABABAA==，求四棱锥111ABBCC−的高．【答案】(1)证明见解析.(2)1【分析】(1)由1AC⊥平面ABC得1ACBC⊥，又因为ACBC⊥，可证BC⊥平面

11ACCA，从而证得平面11ACCA⊥平面11BCCB；(2)过点1A作11AOCC⊥，可证四棱锥的高为1AO,由三角形全等可证1ACAC=，从而证得O为1CC中点，设1ACACx==，由勾股定理可求出x，再由

勾股定理即可求1AO.【详解】（1）证明：因为1AC⊥平面ABC，BC平面ABC,所以1ACBC⊥,又因为90ACB=，即ACBC⊥，1,ACAC平面11ACCA，1ACACC=,所以BC⊥平面11

ACCA，又因为BC平面11BCCB,所以平面11ACCA⊥平面11BCCB.（2）如图，过点1A作11AOCC⊥，垂足为O.因为平面11ACCA⊥平面11BCCB，平面11ACCA平面111BCCBCC=，1AO平面11ACCA，所以1AO⊥平面11BCCB，所以四

棱锥111ABBCC−的高为1AO.因为1AC⊥平面ABC，,ACBC平面ABC,所以1ACBC⊥,1ACAC⊥,又因为1ABAB=，BC为公共边，所以ABC与1ABC全等，所以1ACAC=.设1ACACx==，则11ACx=，所以O为1CC中点，11112OCAA==,又因为1

ACAC⊥,所以22211ACACAA+=,即2222xx+=，解得2x=，所以()22221111211AOACOC=−=−=，所以四棱锥111ABBCC−的高为1．4．（2023·北京·高考真题）如图，在三棱锥−PABC中，PA⊥平面ABC，13P

AABBCPC====，．(1)求证：BC⊥平面PAB；(2)求二面角APCB−−的大小．【答案】(1)证明见解析(2)π3【分析】（1）先由线面垂直的性质证得PABC⊥，再利用勾股定理证得BCPB⊥，从而利用线面垂直的判定定理即可得证；（2）结合（1）中

结论，建立空间直角坐标系，分别求得平面PAC与平面PBC的法向量，再利用空间向量夹角余弦的坐标表示即可得解.【详解】（1）因为PA⊥平面,ABCBC平面ABC，所以PABC⊥，同理PAAB⊥，所以PAB为直角三角形，又因为222PBPAAB=+=，1,3BCPC==，所以222

PBBCPC+=，则PBC为直角三角形，故BCPB⊥，又因为BCPA⊥，PAPBP=，所以BC⊥平面PAB.（2）由（1）BC⊥平面PAB，又AB平面PAB，则BCAB⊥，以A为原点，AB为x轴，过A且与BC平行的直线为y轴，AP为z轴，建立空间直角坐标系，如图，则(0,0,0),(0

,0,1),(1,1,0),(1,0,0)APCB，所以(0,0,1),(1,1,0),(0,1,0),(1,1,1)APACBCPC====−，设平面PAC的法向量为()111,,mxyz=，则00mAPmAC=

=，即1110,0,zxy=+=令11x=，则11y=−，所以(1,1,0)m=−，设平面PBC的法向量为()222,,xnyz=，则00nBCnPC==，即222200yxyz=+−=，令21x=

，则21z=，所以(1,0,1)n=，所以11cos,222mnmnmn===，又因为二面角APCB−−为锐二面角，所以二面角APCB−−的大小为π3.5．（2022·全国甲卷·高考真题）在四棱锥PABCD−中，PD⊥底面,,1,2,3ABCDCDABADDCC

BABDP=====∥．(1)证明：BDPA⊥；(2)求PD与平面PAB所成的角的正弦值．【答案】(1)证明见解析；(2)55.【分析】（1）作DEAB⊥于E，CFAB⊥于F，利用勾股定理证明ADBD⊥，根据线面垂直的性质可得PD

BD⊥，从而可得BD⊥平面PAD，再根据线面垂直的性质即可得证；（2）以点D为原点建立空间直角坐标系，利用向量法即可得出答案.【详解】（1）证明：在四边形ABCD中，作DEAB⊥于E，CFAB⊥于F，因为//,1,2CDABADCDCBAB====，所以四边形ABCD为等腰梯形，所以12AEBF=

=，故32DE=，223BDDEBE=+=，所以222ADBDAB+=，所以ADBD⊥，因为PD⊥平面ABCD，BD平面ABCD，所以PDBD⊥，又=PDADD，所以BD⊥平面PAD，又因为PA平面

PAD，所以BDPA⊥；（2）解：如图，以点D为原点建立空间直角坐标系，3BD=，则()()()1,0,0,0,3,0,0,0,3ABP，则()()()1,0,3,0,3,3,0,0,3APBPDP=−=−=，设平面PAB的法向量(),,nxyz=，则有30{330nAPxznBPyz=

−+==−+=，可取()3,1,1n=，则5cos,5nDPnDPnDP==，所以PD与平面PAB所成角的正弦值为55.6．（2022·全国乙卷·高考真题）如图，四面体ABCD中，,,ADCDADCDA

DBBDC⊥==，E为AC的中点．(1)证明：平面BED⊥平面ACD；(2)设2,60ABBDACB===，点F在BD上，当AFC△的面积最小时，求CF与平面ABD所成的角的正弦值．【答案】(1)证明过程见解析(2)CF与平面AB

D所成的角的正弦值为437【分析】（1）根据已知关系证明ABDCBD≌△△，得到ABCB=，结合等腰三角形三线合一得到垂直关系，结合面面垂直的判定定理即可证明；（2）根据勾股定理逆用得到BEDE⊥，从而建

立空间直角坐标系，结合线面角的运算法则进行计算即可.【详解】（1）因为ADCD=，E为AC的中点，所以ACDE⊥；在ABD△和CBD△中，因为,,BACDCDADBDBDBD===，所以ABDCBD≌△△，所以ABCB=，又因为E为AC的中点，所以ACBE⊥；又因为,DE

BE平面BED，DEBEE=，所以AC⊥平面BED，因为AC平面ACD，所以平面BED⊥平面ACD.（2）连接EF，由（1）知，AC⊥平面BED，因为EF平面BED，所以ACEF⊥，所以1=2AFCSACEF△，当EFBD⊥时，E

F最小，即AFC△的面积最小.因为ABDCBD≌△△，所以2CBAB==，又因为60ACB=，所以ABC是等边三角形，因为E为AC的中点，所以1AEEC==，3BE=，因为ADCD⊥，所以112DEAC==,在DEB中，222DEBEBD+=，所以BEDE⊥.以E为坐标原点建立如

图所示的空间直角坐标系Exyz−，则()()()1,0,0,0,3,0,0,0,1ABD，所以()()1,0,1,1,3,0ADAB=−=−，设平面ABD的一个法向量为(),,nxyz=，则030nADxznABxy=−+==−+=

，取3y=，则()3,3,3n=，又因为()331,0,0,0,,44CF−，所以331,,44CF=，所以643cos,77214nCFnCFnCF===，设CF与平面ABD所成的角为02，所以43sinc

os,7nCF==，所以CF与平面ABD所成的角的正弦值为437.7．（2022·浙江·高考真题）如图，已知ABCD和CDEF都是直角梯形，//ABDC，//DCEF，5AB=，3DC=，1EF=，60BAD

CDE==，二面角FDCB−−的平面角为60．设M，N分别为,AEBC的中点．(1)证明：FNAD⊥；(2)求直线BM与平面ADE所成角的正弦值．【答案】(1)证明见解析；(2)5714．【分析】（1）过点E、D分别做直线DC、AB

的垂线EG、DH并分别交于点G、H，由平面知识易得FCBC=，再根据二面角的定义可知，60BCF=，由此可知，FNBC⊥，FNCD⊥，从而可证得FN⊥平面ABCD，即得FNAD⊥；（2）由（1）可知FN⊥平面ABC

D，过点N做AB平行线NK，所以可以以点N为原点，NK，NB、NF所在直线分别为x轴、y轴、z轴建立空间直角坐标系Nxyz−，求出平面ADE的一个法向量，以及BM，即可利用线面角的向量公式解出．【详解】（1）过点E、D分别做直线DC、AB的垂线EG、DH并分别交于点G、H．∵四边形ABCD和EFC

D都是直角梯形，//,//,5,3,1ABDCCDEFABDCEF===，60BADCDE==，由平面几何知识易知，2,90DGAHEFCDCFDCBABC======，则四边形EFCG和四边形DCBH是矩形，∴在RtEGD和RtDH

A，23EGDH==，∵,DCCFDCCB⊥⊥，且CFCBC=，∴DC⊥平面,BCFBCF是二面角FDCB−−的平面角，则60BCF=，∴BCF△是正三角形，由DC平面ABCD，得平面ABCD⊥平面BCF，∵N是BC的中点，

FNBC⊥，又DC⊥平面BCF，FN平面BCF，可得FNCD⊥，而BCCDC=，∴FN⊥平面ABCD，而AD平面ABCDFNAD⊥．（2）因为FN⊥平面ABCD，过点N做AB平行线NK，所以以点N为原点，NK，NB、NF所在直线分

别为x轴、y轴、z轴建立空间直角坐标系Nxyz−，设(5,3,0),(0,3,0),(3,3,0),(1,0,3)ABDE−，则333,,22M，333,,,(2,23,0),(2,3,3)22BMADDE=−=−−=−

设平面ADE的法向量为(,,)nxyz=由00nADnDE==，得22302330xyxyz−−=−++=，取(3,1,3)n=−，设直线BM与平面ADE所成角为，∴3333322||5357sincos,14|||39723313944n

BMnBMnBM++=====++++．8．（2021·全国新Ⅰ卷·高考真题）如图，在三棱锥ABCD−中，平面ABD⊥平面BCD，ABAD=，O为BD的中点.（1）证明：OACD⊥；（2）若OCD是边长为1的等边三角形，点E在棱AD上，2DE

EA=，且二面角EBCD−−的大小为45，求三棱锥ABCD−的体积.【答案】(1)证明见解析；(2)36.【分析】(1)由题意首先证得线面垂直，然后利用线面垂直的定义证明线线垂直即可；(2)方法二：利用几何关系找到二面角的平面角，然后结合相关的几何

特征计算三棱锥的体积即可.【详解】（1）因为ABAD=，O是BD中点，所以OABD⊥，因为OA平面ABD，平面ABD⊥平面BCD，且平面ABD平面BCDBD=，所以OA⊥平面BCD．因为CD平面BCD，所以OACD⊥.（2）[方法一]：通性通法—坐标法如图所示，以O为坐标原点，

OA为z轴，OD为y轴，垂直OD且过O的直线为x轴，建立空间直角坐标系Oxyz−，则31(,,0),(0,1,0),(0,1,0)22CDB−，设12(0,0,),(0,,)33AmEm,所以4233(0,,),(

,,0)3322EBmBC=−−=，设(),,nxyz=r为平面EBC的法向量，则由00EBnBCn==可求得平面EBC的一个法向量为2(3,1,)nm=−−．又平面BCD的一个法向量为()0,0,OAm=，所以222cos,244nOAmm−==

+，解得1m=．又点C到平面ABD的距离为32，所以1133213226ABCDCABDVV−−===，所以三棱锥ABCD−的体积为36．[方法二]【最优解】：作出二面角的平面角如图所示，作EGB

D⊥，垂足为点G．作GFBC⊥，垂足为点F，连结EF，则OAEG∥．因为OA⊥平面BCD，所以EG⊥平面BCD，EFG为二面角EBCD−−的平面角．因为45EFG=，所以EGFG=．由已知得1OBOD==，故1OBOC==．又30OBCOCB==，所以3BC=．因为242

22,,,,133333GDGBFGCDEGOA======，11113322(11)1333226ABCDBCDBOCVSOSOAA−====．[方法三]：三面角公式考虑三面角BEDC−，记EBD为，EBC为，30DBC=，记二面角EBCD−−为．据题意，得45

=．对使用三面角的余弦公式，可得coscoscos30=，化简可得3coscos2=．①使用三面角的正弦公式，可得sinsinsin=，化简可得sin2sin=．②将①②两式平方后相加，可得223cos2sin14+=，由此得221sincos4=

，从而可得1tan2=．如图可知π(0,)2，即有1tan2=，根据三角形相似知，点G为OD的三等分点，即可得43BG=，结合的正切值，可得2,13EGOA==从而可得三棱锥ABCD−的体积为36．【

整体点评】(2)方法一：建立空间直角坐标系是解析几何中常用的方法，是此类题的通性通法，其好处在于将几何问题代数化，适合于复杂图形的处理；方法二：找到二面角的平面角是立体几何的基本功，在找出二面角的同时可以对几何体的几何特征有更加深刻的认识，该法为

本题的最优解.方法三：三面角公式是一个优美的公式，在很多题目的解析中灵活使用三面角公式可以使得问题更加简单、直观、迅速.9．（2021·全国新Ⅱ卷·高考真题）在四棱锥QABCD−中，底面ABCD是正方形，若2,5,3ADQDQAQC====．（1）证明：平面QAD⊥平面ABC

D；（2）求二面角BQDA−−的平面角的余弦值．【答案】（1）证明见解析；（2）23.【分析】（1）取AD的中点为O，连接,QOCO，可证QO⊥平面ABCD，从而得到面QAD⊥面ABCD.（2）在平面ABCD内，过O作//OTCD，交BC于T，则OTAD⊥，建如

图所示的空间坐标系，求出平面QAD、平面BQD的法向量后可求二面角的余弦值.【详解】（1）取AD的中点为O，连接,QOCO.因为QAQD=，OAOD=，则QO⊥AD，而2,5ADQA==，故512QO=−=.在正方形ABCD中，因为2AD=，故1DO=，故5CO=，因为3QC=，故222Q

CQOOC=+，故QOC为直角三角形且QOOC⊥，因为OCADO=，故QO⊥平面ABCD，因为QO平面QAD，故平面QAD⊥平面ABCD.（2）在平面ABCD内，过O作//OTCD，交BC于T，则OTAD⊥，结合（1）中的QO⊥平面ABCD，故可建如图所示的空间坐标系.则()()()0,1

,0,0,0,2,2,1,0DQB−，故()()2,1,2,2,2,0BQBD=−=−.设平面QBD的法向量(),,nxyz=，则00nBQnBD==即220220xyzxy−++=−+=，取1x=，则11,2yz==，故11,1,2n=.而平面QAD的法

向量为()1,0,0m=，故12cos,3312mn==.二面角BQDA−−的平面角为锐角，故其余弦值为23.10．（2021·全国甲卷·高考真题）已知直三棱柱111ABCABC-中，侧面11AABB为正方形，2ABBC==，E，F分别为AC和1CC的中点，D为棱11AB上

的点．11BFAB⊥（1）证明：BFDE⊥；（2）当1BD为何值时，面11BBCC与面DFE所成的二面角的正弦值最小?【答案】（1）证明见解析；（2）112BD=【分析】（1）方法二：通过已知条件，确定三

条互相垂直的直线，建立合适的空间直角坐标系，借助空间向量证明线线垂直；（2）方法一：建立空间直角坐标系，利用空间向量求出二面角的平面角的余弦值最大，进而可以确定出答案；【详解】（1）[方法一]：几何法因为

1111,//BFABABAB⊥，所以BFAB⊥．又因为1ABBB⊥，1BFBBB=，所以AB⊥平面11BCCB．又因为2ABBC==，构造正方体1111ABCGABCG−，如图所示，过E作AB的平行线分别与AGBC，交于其中点,MN，连接11,AMBN，因为E，F分别为AC和1CC的

中点，所以N是BC的中点，易证1RtRtBCFBBN，则1CBFBBN=．又因为1190BBNBNB+=，所以1190CBFBNBBFBN+=⊥，．又因为111111,BFABBNABB⊥=，所以BF⊥平面11AMNB．又因为ED平面11AMNB，所以BFDE⊥．[方法

二]【最优解】：向量法因为三棱柱111ABCABC-是直三棱柱，1BB⊥底面ABC，1BBAB⊥11//ABAB，11BFAB⊥，BFAB⊥，又1BBBFB=，AB⊥平面11BCCB．所以1,,BABCBB两两垂直．以B为坐标原点，分别以1,,BABCBB所在直线为,,xyz

轴建立空间直角坐标系，如图．()()()0,0,0,2,0,0,0,2,0,BAC()()()1110,0,2,2,0,2,0,2,2BAC，()()1,1,0,0,2,1EF．由题设(),0,2Da（02a）．因为()()0,2,1,1,1,2BFDEa==−−，所以()

()0121120BFDEa=−++−=，所以BFDE⊥．[方法三]：因为11BFAB⊥，11//ABAB，所以BFAB⊥，故110BFAB=，0BFAB=，所以()11BFEDBFEBBBBD=++()11=BFBDBFEBBB++1BFEBBFBB=+1

1122BFBABCBFBB=−−+11122BFBABFBCBFBB=−−+112BFBCBFBB=−+111coscos2BFBCFBCBFBBFBB=−+121=52520255−+=，

所以BFED⊥．（2）[方法一]【最优解】：向量法设平面DFE的法向量为(),,mxyz=，因为()()1,1,1,1,1,2EFDEa=−=−−，所以00mEFmDE==，即()0120xyzaxyz−++=−+−

=．令2za=−，则()3,1,2maa=+−因为平面11BCCB的法向量为()2,0,0BA=，设平面11BCCB与平面DEF的二面角的平面角为，则cosmBAmBA=2622214aa=−+232214aa=−+．当12a=时，

22214aa−+取最小值为272，此时cos取最大值为363272=．所以()2min63sin133=−=，此时112BD=．[方法二]：几何法如图所示，延长EF交11AC的延长线于点S，联结DS交11BC于点T，则平面DFE平面11BBCC

FT=．作1BHFT⊥，垂足为H，因为1DB⊥平面11BBCC，联结DH，则1DHB为平面11BBCC与平面DFE所成二面角的平面角．设1,BDt=[0,2],t1BTs=，过1C作111//CGAB交DS于点G．由111113CSCGSAAD==得11(2)3CGt=−．又1111BDBT

CGCT=，即12(2)3tsst=−−，所以31tst=+．又111BHBTCFFT=，即1211(2)BHss=+−，所以121(2)sBHs=+−．所以2211DHBHBD=+2221(2)sts=++−2229225tttt=+−+．则11s

inBDDHBDH=2229225ttttt=+−+219119222t=+−+，所以，当12t=时，()1min3sin3DHB=．[方法三]：投影法如图，联结1,FBFN，DEF在平面11BBCC的投影为1BNF，记面11BBCC与面DFE所成的二面

角的平面角为，则1cosBNFDEFSS=．设1(02)BDtt=，在1RtDBF中，222115DFBDBFt=+=+．在RtECF中，223EFECFC=+=，过D作1BN的平行线交EN于点Q．在RtDEQ△中，2225(1)DEQDEQt=+=+−．在DEF中，

由余弦定理得222cos2DFEFDEDFEDFEF+−=()22315(1)35ttt++=+，()222214sin35ttDFEt−+=+，1sin2DFESDFEFDFE=2122142tt=−+，13,2BNF

S=1cosBNFDFESS=232214tt=−+，()29sin127tt=−−+，当12t=，即112BD=，面11BBCC与面DFE所成的二面角的正弦值最小，最小值为33．【整体点评】第一问，方法一为常规方法，不过这道

题常规方法较为复杂，方法二建立合适的空间直角坐标系，借助空间向量求解是最简单，也是最优解；方法三利用空间向量加减法则及数量积的定义运算进行证明不常用，不过这道题用这种方法过程也很简单，可以开拓学生的思维.第二问：方法一建立空间直角坐标系，利用空间向量求出二面角的平面角是最常规的方法，也是最优方

法；方法二：利用空间线面关系找到，面11BBCC与面DFE所成的二面角，并求出其正弦值的最小值，不是很容易找到；方法三：利用面DFE在面11BBCC上的投影三角形的面积与DFE△面积之比即为面11BBCC与面DFE所成的二面角的

余弦值，求出余弦值的最小值，进而求出二面角的正弦值最小，非常好的方法，开阔学生的思维．11．（2021·全国乙卷·高考真题）如图，四棱锥PABCD−的底面是矩形，PD⊥底面ABCD，M为BC的中点，且PBAM⊥．（1）证明：平面PAM⊥平面PBD；（2）若1PDDC==，求四棱锥PABCD−的体积

．【答案】（1）证明见解析；（2）23．【分析】（1）由PD⊥底面ABCD可得PDAM⊥，又PBAM⊥，由线面垂直的判定定理可得AM⊥平面PBD，再根据面面垂直的判定定理即可证出平面PAM⊥平面PBD；（2）由（1）可知，AMBD⊥，由平面知识可知，~DABABM，由相似

比可求出AD，再根据四棱锥PABCD−的体积公式即可求出．【详解】（1）因为PD⊥底面ABCD，AM平面ABCD，所以PDAM⊥，又PBAM⊥，PBPDP=，所以AM⊥平面PBD，而AM平面PAM，所以平面PAM⊥平面PBD．（2）[方法一]

：相似三角形法由（1）可知AMBD⊥．于是∽ABDBMA，故=ADABABBM．因为1,,12===BMBCADBCAB，所以2112BC=，即2BC=．故四棱锥PABCD−的体积1233==VABBCPD．[

方法二]：平面直角坐标系垂直垂直法由（2）知⊥AMDB,所以1=−AMBDkk．建立如图所示的平面直角坐标系，设2(0)BCaa=．因为1DC=，所以(0,0)A，(1,0)B，(0,2)Da，()1,Ma．从而2020(2)2

11001−−==−=−=−−−AMBDaakkaaa．所以22a=，即2DA=．下同方法一.[方法三]【最优解】：空间直角坐标系法建立如图所示的空间直角坐标系Dxyz−，设||=DAt，所以(0,0,0)D，(0,1,0)C，(0,0,1)P，(,0,0)At

，(,1,0)Bt．所以,1,02tM，(,1,1)PBt=−，,1,02tAM=−．所以2110(1)1022ttPBAMt=−++−=−+=．所以2t=，即||2=DA．下同方法一.[

方法四]：空间向量法由PBAM⊥，得0PBAM=．所以()0++=PDDAABAM．即0++=PDAMDAAMABAM．又PD⊥底面ABCD，AM在平面ABCD内，因此PDAM⊥，所以0=PDAM．所以0+=DAAMABAM，由于四边形ABCD是矩形，根据数量积的几何意义，

得221||||02−+=DAAB，即21||102−+=BC．所以||2BC=，即2BC=．下同方法一.【整体点评】(2)方法一利用相似三角形求出求出矩形的另一个边长，从而求得该四棱锥的体积；方法二构建平面直角坐标系，利用直线垂直的条件得到矩形的另一个

边长，从而求得该四棱锥的体积；方法三直接利用空间直角坐标系和空间向量的垂直的坐标运算求得矩形的另一个边长,为最常用的通性通法，为最优解；方法四利用空间向量转化求得矩形的另一边长.12．（2021·浙江·高考真题）如图，在四棱锥PABCD−中，底面ABCD是平行四

边形，120,1,4,15ABCABBCPA====，M，N分别为,BCPC的中点，,PDDCPMMD⊥⊥.（1）证明：ABPM⊥；（2）求直线AN与平面PDM所成角的正弦值.【答案】（1）证明见解析；（2）156．【

分析】（1）要证ABPM⊥，可证DCPM⊥，由题意可得，PDDC⊥，易证DMDC⊥，从而DC⊥平面PDM，即有DCPM⊥，从而得证；（2）取AD中点E，根据题意可知，,,MEDMPM两两垂直，所以以点M为坐标原点，建立空间直角坐标系，再分别求出向量AN和平面PDM的一个法向量，

即可根据线面角的向量公式求出．【详解】（1）在DCM△中，1DC=，2CM=，60DCM=，由余弦定理可得3DM=，所以222DMDCCM+=，DMDC⊥．由题意DCPD⊥且PDDMD=，DC⊥平面PDM，而PM平面PDM，所以DCPM⊥，又//ABDC，所以ABPM⊥

．（2）由PMMD⊥，ABPM⊥，而AB与DM相交，所以PM⊥平面ABCD，因为7AM=，所以22PM=，取AD中点E，连接ME，则,,MEDMPM两两垂直，以点M为坐标原点，如图所示，建立空间直角坐标系,则(3,2,0),(0,0,22),(3

,0,0)APD−,(0,0,0),(3,1,0)MC−又N为PC中点，所以31335,,2,,,22222NAN−=−.由（1）得CD⊥平面PDM，所以平面PDM的一个法向量(0,1,0)n=从而直线AN与平面PD

M所成角的正弦值为5||152sin6||2725244ANnANn===++‖．【点睛】本题第一问主要考查线面垂直的相互转化，要证明ABPM⊥，可以考虑DCPM⊥，题中与DC有垂直关系的直线较多，易证DC⊥平面PDM，从而使问题得以解决；第二问思路直接

，由第一问的垂直关系可以建立空间直角坐标系，根据线面角的向量公式即可计算得出．13．（2020·海南·高考真题）如图，四棱锥P-ABCD的底面为正方形，PD⊥底面ABCD．设平面PAD与平面PBC的交线为l．（1）证明：l⊥平面PD

C；（2）已知PD=AD=1，Q为l上的点，QB=2，求PB与平面QCD所成角的正弦值．【答案】（1）证明见解析；（2）63.【分析】（1）利用线面平行的判定定理以及性质定理，证得//ADl，利用线面垂直的判定定理证得AD⊥

平面PDC，从而得到l⊥平面PDC；（2）根据题意，建立相应的空间直角坐标系，得到相应点的坐标，设出点(,0,1)Qm，之后求得平面QCD的法向量以及向量PB的坐标，求得cos,nPB，即可得到直线P

B与平面QCD所成角的正弦值.【详解】（1）证明：在正方形ABCD中，//ADBC，因为AD平面PBC，BC平面PBC，所以//AD平面PBC，又因为AD平面PAD，平面PAD平面PBCl=，所以//ADl，因为在四棱锥PABCD−中，底面ABCD是正方形，所

以,,ADDClDC⊥⊥且PD⊥平面ABCD，所以,,ADPDlPD⊥⊥因为CDPDD=所以l⊥平面PDC；（2）如图建立空间直角坐标系Dxyz−，因为1PDAD==，则有(0,0,0),(0,1,0),(1,0,0

),(0,0,1),(1,1,0)DCAPB，设(,0,1)Qm，则有(0,1,0),(,0,1),(1,1,1)DCDQmPB===−，因为QB=2，所以有222(1)(01)(10)21mm−+−+−==设平面QCD的法向量为(,,)nxyz=，则00DCnDQn=

=，即00yxz=+=，令1x=，则1z=−，所以平面QCD的一个法向量为(1,0,1)n=−，则22222210126cos,.32310(1)111nPBnPBnPB++====++−++根据直线的方

向向量与平面法向量所成角的余弦值的绝对值即为直线与平面所成角的正弦值，所以直线与平面所成角的正弦值等于6|cos,|3nPB=ruur所以直线PB与平面QCD所成角的正弦值为63.【点睛】该题考查的是有关立体几何的问题，涉及到的知识点有线面

平行的判定和性质，线面垂直的判定和性质，利用空间向量求线面角，利用基本不等式求最值，属于中档题目.14．（2020·天津·高考真题）如图，在三棱柱111ABCABC-中，1CC⊥平面,,2ABCACBCACBC⊥==，13CC=，点,DE分别在棱1AA和棱1CC上，且

12,ADCEM==为棱11AB的中点．（Ⅰ）求证：11CMBD⊥；（Ⅱ）求二面角1BBED−−的正弦值；（Ⅲ）求直线AB与平面1DBE所成角的正弦值．【答案】（Ⅰ）证明见解析；（Ⅱ）306；（Ⅲ）33.【分

析】以C为原点，分别以1,,CACBCC的方向为x轴，y轴，z轴的正方向建立空间直角坐标系.（Ⅰ）计算出向量1CM和1BD的坐标，得出110CMBD=，即可证明出11CMBD⊥；（Ⅱ）可知平面1BBE的一个法向量为CA，计

算出平面1BED的一个法向量为n，利用空间向量法计算出二面角1BBED−−的余弦值，利用同角三角函数的基本关系可求解结果；（Ⅲ）利用空间向量法可求得直线AB与平面1DBE所成角的正弦值.【详解】依题意，以C为原点，分别以CA、CB、1C

C的方向为x轴、y轴、z轴的正方向建立空间直角坐标系（如图），可得()0,0,0C、()2,0,0A、()0,2,0B、()10,0,3C、()12,0,3A、()10,2,3B、()2,0,1D、()0,0,2E、()1,1

,3M.（Ⅰ）依题意，()11,1,0CM=，()12,2,2BD=−−，从而112200CMBD=−+=，所以11CMBD⊥；（Ⅱ）依题意，()2,0,0CA=是平面1BBE的一个法向量，()10,2,1EB=，()2,0,1ED=−．设

(),,nxyz=为平面1DBE的法向量，则100nEBnED==，即2020yzxz+=−=，不妨设1x=，可得()1,1,2n=−．26cos,626CCAnACnAn===，230sin,1

cos,6CAnCAn=−=．所以，二面角1BBED−−的正弦值为306；（Ⅲ）依题意，()2,2,0AB=−．由（Ⅱ）知()1,1,2n=−为平面1DBE的一个法向量，于是43cos,3226ABnABnABn−===−．所以，直线AB与平面1DBE

所成角的正弦值为33.【点睛】本题考查利用空间向量法证明线线垂直，求二面角和线面角的正弦值，考查推理能力与计算能力，属于中档题.15．（2020·浙江·高考真题）如图，三棱台ABC—DEF中，平面AC

FD⊥平面ABC，∠ACB=∠ACD=45°，DC=2BC．（I）证明：EF⊥DB；（II）求DF与面DBC所成角的正弦值．【答案】（I）证明见解析；（II）33【分析】（I）方法一：作DHAC⊥交AC于H，连接BH，

由题意可知DH⊥平面ABC，即有DHBC⊥，根据勾股定理可证得BCBH⊥，又//EFBC，可得DHEF⊥，BHEF⊥，即得EF⊥平面BHD，即证得EFDB⊥；（II）方法一：由//DFCH，所以DF与平面DBC所成角即为CH与平面DB

C所成角，作HGBD⊥于G，连接CG，即可知HCG即为所求角，再解三角形即可求出DF与平面DBC所成角的正弦值．【详解】（I）[方法一]：几何证法作DHAC⊥交AC于H，连接BH．∵平面ADFC⊥平面AB

C，而平面ADFC平面ABCAC=，DH平面ADFC，∴DH⊥平面ABC，而BC平面ABC，即有DHBC⊥．∵45ACBACD==，∴222CDCHBCCHBC===．在CBH中，22222cos45BHCHBCCHBCBC=+−=，即有222BHBCCH

+=，∴BHBC⊥．由棱台的定义可知，//EFBC，所以DHEF⊥，BHEF⊥，而BHDHH=，∴EF⊥平面BHD，而BD平面BHD，∴EFDB⊥．[方法二]【最优解】：空间向量坐标系方法作DOAC⊥交AC于O．∵平面ADFC⊥平面ABC，而平面ADFC平

面ABCAC=，DO平面ADFC，∴DO⊥平面ABC，以O为原点，建立空间直角坐标系如图所示.设OC=1,∵45ACBACD==，22DCBC==，∴22BC=,∴()()110,0,1,0,1,0,,,022DCB，∴11,,122BD=−−,11,,022B

C=−,11·044BDBC=−=,∴BC⊥BD,又∵棱台中BC//EF,∴EF⊥BD；[方法三]：三余弦定理法∵平面ACFD⊥平面ABC，∴1coscoscoscos45cos452BCDACBACD===,∴60BCD=，又∵DC

=2BC．∴90CBD=,即CBBD⊥,又∵//EFBC，∴EFDB⊥．（II）[方法一]：几何法因为//DFCH，所以DF与平面DBC所成角即为与CH平面DBC所成角．作HGBD⊥于G，连接CG，由（1）可知，BC⊥平面BHD，因为所以平面BCD⊥平面BHD，而平面BCD平面BH

DBD=，HG平面BHD，∴HG⊥平面BCD．即CH在平面DBC内的射影为CG，HCG即为所求角．在RtHGC△中，设BCa=，则2CHa=，2233BHDHaaHGaBDa===，∴13sin33HGHCGCH===．故DF与

平面DBC所成角的正弦值为33．[方法二]【最优解】：空间向量坐标系法设平面BCD的法向量为(),,nxyz=,由（I）得11,,122BD=−−,11,,022BC=−,∴11022,11022xyzxy−−+=−+=令1x=,则1y

=,2z=,()1,1,1n=,()0,1,0OC=，13cos,3111?1nOC==++,由于//DFOC，∴直线DF与平面DBC所成角的正弦值为33．[方法三]：空间向量法以{,,}CHCBCD为基底,不妨设22D

CBC==，则3,2,45,45,60DBCHHCBHCDDCB=====(由（I）的结论可得）．设平面DBC的法向量为nxCHyCBzCD=++，则由0,0,nCDnCB==得240,0,xyzxyz++=++=取1z=，得32nCHCBCD

=−++．设直线DF与平面DBC所成角为，则直线HC与平面DBC所成角也为，由公式得||23sin3||||26HCnHCn===．[方法四]：三余弦定理法由45ACBACD==，可知H在平面DBC的

射影G在DCB的角平分线上．设直线DF与平面DBC所成角为，则HC与平面DBC所成角也为．由由（I）的结论可得60BCD=，由三余弦定理，得cos45cos30cos=，6cos3=从而3sin3=．[方法五]：等体积法设H到平面

DBC的距离为h，设1DH=,则261,2,,22HCDCBCBD====,设直线DF与平面DBC所成角为，由已知得HC与平面DBC所成角也为．由HDBCDHBCVV−−=，1121122sin601451322322hsin=,求得33h=，所

以333sin13hHC===．【整体评价】（I）的方法一使用几何方法证明，方法二利用空间直角坐标系方法，简洁清晰，通性通法，确定为最优解；方法三使用了两垂直角的三余弦定理得到60BCD=，进而证明，过程简洁，确定为最优解（II）的方法一使用几何做法，方法二使

用空间坐标系方法，为通性通法，确定为最优解；方法三使用空间向量的做法，避开了辅助线的求作；方法四使用三余弦定理法，最为简洁，确定为最优解；方法五采用等体积转化法，避免了较复杂的辅助线.16．（2020·山东·高考真题）如图，四棱锥P-ABCD的底面为正方形，PD⊥底面ABC

D．设平面PAD与平面PBC的交线为l．（1）证明：l⊥平面PDC；（2）已知PD=AD=1，Q为l上的点，求PB与平面QCD所成角的正弦值的最大值．【答案】（1）证明见解析；（2）63.【分析】（1）利用线面垂直的判定定理证得AD⊥平面PDC，利用线面平行的判定

定理以及性质定理，证得//ADl，从而得到l⊥平面PDC；（2）方法一：根据题意，建立相应的空间直角坐标系，得到相应点的坐标，设出点(,0,1)Qm，之后求得平面QCD的法向量以及向量PB的坐标，求得cos

,nPB的最大值，即为直线PB与平面QCD所成角的正弦值的最大值.【详解】（1）证明：在正方形ABCD中，//ADBC，因为AD平面PBC，BC平面PBC，所以//AD平面PBC，又因为AD平面PAD，平面PAD

平面PBCl=，所以//ADl，因为在四棱锥PABCD−中，底面ABCD是正方形，所以,,ADDClDC⊥⊥且PD⊥平面ABCD，所以,,ADPDlPD⊥⊥因为CDPDD=，所以l⊥平面PDC．（2

）［方法一］【最优解】：通性通法因为,,DPDADC两两垂直，建立空间直角坐标系Dxyz−，如图所示：因为1PDAD==，设(0,0,0),(0,1,0),(1,0,0),(0,0,1),(1,1,0)DC

APB，设(,0,1)Qm，则有(0,1,0),(,0,1),(1,1,1)DCDQmPB===−，设平面QCD的法向量为(,,)nxyz=，则00DCnDQn==，即00ymxz=+=，令1x=，则zm=−，所以平面QCD的一个法向量为(1,0,)nm=−，则210cos,31n

PBmnPBnPBm++==+根据直线的方向向量与平面法向量所成角的余弦值的绝对值即为直线与平面所成角的正弦值，所以直线PB与平面QCD所成角的正弦值等于2|1||cos,|31mnPBm+=+ruur2231231mmm++=+223232||36

1111313133mmmm=+++=++，当且仅当1m=时取等号，所以直线PB与平面QCD所成角的正弦值的最大值为63.［方法二］：定义法如图2，因为l平面PBC，Ql，所以Q平面PBC．在平面PQC中，设P

BQCE=．在平面PAD中，过P点作PFQD⊥，交QD于F，连接EF．因为PD⊥平面,ABCDDC平面ABCD，所以DCPD⊥．又由,,DCADADPDDPD⊥=平面PAD，AD平面PAD，所以DC⊥平面PAD．又PF

平面PAD，所以DCPF⊥．又由,,PFQDQDDCDQD⊥=平面,QOCDC平面QDC，所以PF⊥平面QDC，从而FEP即为PB与平面QCD所成角．设PQa=，在PQD△中，易求21aPFa=+．由PQEV与BEC相似，得1PEPQaEBBC==，可得31aPEa=

+．所以22211226sin1313333aaFEPaa+==+=++，当且仅当1a=时等号成立．［方法三］：等体积法如图3，延长CB至G，使得BGPQ=，连接GQ，GD，则//PBQG，过G点作GM⊥平面

QDC，交平面QDC于M，连接QM，则GQM即为所求．设PQx=，在三棱锥QDCG−中，111()(1)326QDCGVPDCDCBBGx−=+=+．在三棱锥GQDC−中，2111113232GQDCVGMCDQDGMx−==+．由QDCGGQDCVV

−−=得2111(1)1632xGMx+=+，解得2222112212111xxxxGMxxx+++===++++，当且仅当1x=时等号成立．在RtPDB△中，易求3PBQG==，所以直线PB与平面QCD所成角的正弦值的最大值为2

6sin33MQG==．【整体点评】（2）方法一：根据题意建立空间直角坐标系，直线PB与平面QCD所成角的正弦值即为平面QCD的法向量n与向量PB的夹角的余弦值的绝对值，即cos,nPB，再根据基本不等式即可求出

，是本题的通性通法，也是最优解；方法二：利用直线与平面所成角的定义，作出直线PB与平面QCD所成角，再利用解三角形以及基本不等式即可求出；方法三：巧妙利用//PBQG，将线转移，再利用等体积法求得点面距，利用直

线PB与平面QCD所成角的正弦值即为点面距与线段长度的比值的方法，即可求出．17．（2020·全国·高考真题）如图，在长方体1111ABCDABCD−中，点E，F分别在棱1DD，1BB上，且12DEED=，12BFFB=．证明：（1）

当ABBC=时，EFAC⊥；（2）点1C在平面AEF内．【答案】（1）证明见解析；（2）证明见解析.【分析】（1）根据正方形性质得ACBD⊥，根据长方体性质得1ACBB⊥,进而可证AC⊥平面11BBDD,

即得结果；（2）只需证明1//ECAF即可，在1CC上取点M使得12CMMC=,再通过平行四边形性质进行证明即可.【详解】（1）因为长方体1111ABCDABCD−,所以1BB⊥平面ABCD1ACBB⊥,因为长方体1111,AB

CDABCDABBC−=,所以四边形ABCD为正方形ACBD⊥因为11,BBBDBBBBD=I、平面11BBDD,因此AC⊥平面11BBDD,因为EF平面11BBDD,所以ACEF⊥；（2）在1CC上取点M使得12CMMC=,连,DMMF

,因为111112,//,=DEEDDDCCDDCC=,所以11,//,EDMCEDMC=所以四边形1DMCE为平行四边形，1//DMEC因为//,=,MFDAMFDA所以MFAD、、、四点共面，所以四边形MFAD为平行四边形，1//,//DMAFECAF，所以

1ECAF、、、四点共面，因此1C在平面AEF内【点睛】本题考查线面垂直判定定理、线线平行判定，考查基本分析论证能力，属中档题.18．（2020·全国·高考真题）如图，D为圆锥的顶点，O是圆锥底面的圆心，ABC是底面的内接正三角形，P为D

O上一点，∠APC=90°．（1）证明：平面PAB⊥平面PAC；（2）设DO=2，圆锥的侧面积为3π，求三棱锥P−ABC的体积.【答案】（1）证明见解析；（2）68.【分析】（1）根据已知可得PAPBPC==，进而有PAC△≌PBC

，可得90APCBPC==，即PBPC⊥，从而证得PC⊥平面PAB，即可证得结论；（2）将已知条件转化为母线l和底面半径r的关系，进而求出底面半径，由正弦定理，求出正三角形ABC边长，在等腰直角三角形APC中求出AP，在RtAPO中，求出PO，即可求出结论.【详解】（1）连接,,O

AOBOC，D为圆锥顶点，O为底面圆心，OD⊥平面ABC，P在DO上，,OAOBOCPAPBPC====，ABC是圆内接正三角形，ACBC=，PAC△≌PBC，90APCBPC==，即,PBPCPAPC⊥⊥，,PAPBPPC=⊥平面,PABPC平面

PAC，平面PAB⊥平面PAC；（2）设圆锥的母线为l，底面半径为r，圆锥的侧面积为3,3rlrl==，2222ODlr=−=，解得1,3rl==，2sin603ACr==，在等腰直角三角形APC中，2622APAC==，在RtPAO中，2262142POAPOA=

−=−=，三棱锥−PABC的体积为11236333248PABCABCVPOS−===△.【点睛】本题考查空间线、面位置关系，证明平面与平面垂直，求锥体的体积，注意空间垂直间的相互转化，考查逻辑推理、直观想象、数学计算能力，属

于中档题.19．（2020·全国·高考真题）如图，D为圆锥的顶点，O是圆锥底面的圆心，AE为底面直径，AEAD=．ABC是底面的内接正三角形，P为DO上一点，66PODO=．（1）证明：PA⊥平面PBC；（2）求二面角BPCE−−的余弦值．【答案】（1）证明见解析；（2）255.【

分析】（1）要证明PA⊥平面PBC，只需证明PAPB⊥，PAPC⊥即可；（2）方法一：过O作ON∥BC交AB于点N，以O为坐标原点，OA为x轴，ON为y轴建立如图所示的空间直角坐标系，分别算出平面PCB的一个法

向量n，平面PCE的一个法向量为m，利用公式cos,||||nmmnnm=计算即可得到答案.【详解】（1）[方法一]：勾股运算法证明由题设，知DAE为等边三角形，设1AE=，则32DO=，1122COBOAE===，所以62

64PODO==，2264PCPOOCPBPA=+===又ABC为等边三角形，则2sin60BAOA=，所以32BA=，22234PAPBAB+==，则90APB=，所以PAPB⊥，同理PAPC⊥，又PCPBP=，所以PA⊥

平面PBC；[方法二]：空间直角坐标系法不妨设23AB=，则4sin60===ABAEAD，由圆锥性质知DO⊥平面ABC，所以22224223=−=−=DOADAO，所以626==PODO．因为O是ABC的外心，因此AEBC⊥．

在底面过O作BC的平行线与AB的交点为W，以O为原点，OW方向为x轴正方向，OE方向为y轴正方向，OD方向为z轴正方向，建立空间直角坐标系Oxyz−，则(0,2,0)A−，(3,1,0)B，(3,1,0

)C−，(0,2,0)E，(0,0,2)P．所以(0,2,2)AP=，(3,1,2)=−−BP，(3,1,2)=−CP．故0220=−+=APBP，0220=−+=APCP．所以APBP⊥，APCP⊥．又BPCPP=

，故AP⊥平面PBC．[方法三]：因为ABC是底面圆O的内接正三角形，且AE为底面直径，所以AEBC⊥．因为DO（即PO）垂直于底面，BC在底面内，所以POBC⊥．又因为PO平面PAE，AE平面PAE，PO

AEO=I，所以BC⊥平面PAE．又因为PA平面PAE，所以PABC⊥．设AEBCF=，则F为BC的中点，连结PF．设DOa=，且66PODO=，则32AFa=，22PAa=，12PFa=．因此222+=PAPFAF，从而PAPF⊥．又因为PFBCF=，所以PA⊥平面PBC．[方

法四]：空间基底向量法如图所示，圆锥底面圆O半径为R，连结DE，AEADDE==，易得3ODR=，因为66=POOD，所以22=POR．以,,OAOBOD为基底，OD⊥平面ABC，则66=+=−+APAOOPOAOD，66=+=−+BPBOOPOBOD，且212OAOBR=−，0OAO

DOBOD==所以6666=−+−+=APBPOAODOBOD26610666−−+=OAOBOAODOBODOD．故0APBP=．所以APBP⊥，即APBP⊥．同理APCP⊥．又BPCPP=，所以AP⊥平面PBC．（2）[方法一]：空

间直角坐标系法过O作ON∥BC交AB于点N，因为PO⊥平面ABC，以O为坐标原点，OA为x轴，ON为y轴建立如图所示的空间直角坐标系，则121313(,0,0),(0,0,),(,,0),(,,0)244444EPBC−−−−，132(,,)444PC=−

−−，132(,,)444PB=−−，12(,0,)24PE=−−，设平面PCB的一个法向量为111(,,)nxyz=，由00nPCnPB==，得111111320320xyzxyz−−−=−+−=

，令12x=，得111,0zy=−=，所以(2,0,1)n=−，设平面PCE的一个法向量为222(,,)mxyz=由00mPCmPE==，得22222320220xyzxz−−−=−−=，令21x=，得2232,3zy=−=，所以3(1,,2)3m

=−故2225cos,5||||1033nmmnnm===，设二面角BPCE−−的大小为，由图可知二面角为锐二面角，所以25cos5=.[方法二]【最优解】：几何法设=BCAEF，易知F是BC的中点，过F作∥FGAP交PE于G，取PC的中点H，联结

GH，则∥HFPB．由PA⊥平面PBC，得FG⊥平面PBC．由（1）可得，222BCPBPC=+，得PBPC⊥．所以FHPC⊥，根据三垂线定理，得GHPC⊥．所以GHF是二面角BPCE−−的平面角．设圆O的半

径为r，则3sin602==AFABr，2AEr=，12=EFr，13EFAF=，所以14=FGPA，1122==FHPBPA，12=FGFH．在RtGFH中，1tan2==FGGHFFH，25cos5=GHF．所以二面角BPCE−−的余弦值为255

．[方法三]：射影面积法如图所示，在PE上取点H，使14HEPE=，设BCAEN=，连结NH．由（1）知14NEAE=，所以∥NHPA．故NH⊥平面PBC．所以，点H在面PBC上的射影为N．故由射影面积法可知二面角BPCE−−的余弦值为cosPCNPC

HSθS=．在PCE中，令62==PCPE，则1CE=，易知54=PCES．所以335416PCHPCESS==．又1328PCNPBCSS==，故3258cos53516PCNPCHSθS===所以二面角BPCE−−

的余弦值为255．【整体点评】本题以圆锥为载体，隐含条件是圆锥的轴垂直于底面，（1）方法一：利用勾股数进行运算证明，是在给出数据去证明垂直时的常用方法；方法二：选择建系利用空间向量法，给空间立体感较弱的学生提

供了可行的途径；方法三：利用线面垂直，结合勾股定理可证出；方法四：利用空间基底解决问题，此解法在解答题中用的比较少；（2）方法一：建系利用空间向量法求解二面角，属于解答题中求角的常规方法；方法二：利用几何

法，通过三垂线法作出二面角，求解三角形进行求解二面角，适合立体感强的学生；方法三：利用射影面积法求解二面角，提高解题速度.20．（2020·全国·高考真题）如图，已知三棱柱ABC–A1B1C1的底面是正三角形，侧面BB1

C1C是矩形，M，N分别为BC，B1C1的中点，P为AM上一点．过B1C1和P的平面交AB于E，交AC于F．（1）证明：AA1//MN，且平面A1AMN⊥平面EB1C1F；（2）设O为△A1B1C1的中心，若AO=AB=6，AO//平面EB1C1F，且∠M

PN=π3，求四棱锥B–EB1C1F的体积．【答案】（1）证明见解析；（2）24.【分析】（1）由,MN分别为BC，11BC的中点，1//MNCC，根据条件可得11//AABB，可证1MNAA//，要证平面11EBCF

⊥平面1AAMN，只需证明EF⊥平面1AAMN即可；（2）根据已知条件求得11EBCFS四边形和M到PN的距离，根据锥体体积公式，即可求得11BEBCFV−.【详解】（1）,MN分别为BC，11BC的中点，1//MNBB又11//AABB1//MNAA在等边ABC中，M为BC中点，则B

CAM⊥又侧面11BBCC为矩形，1BCBB⊥1//MNBBMNBC⊥由MNAMM=，,MNAM平面1AAMNBC⊥平面1AAMN又11//BCBC，且11BC平面ABC，BC平面ABC，11//BC平面

ABC又11BC平面11EBCF，且平面11EBCF平面ABCEF=11//BCEF//EFBC又BC⊥平面1AAMNEF⊥平面1AAMNEF平面11EBCF平面11EBCF⊥平面1AAMN（2）过M作

PN垂线，交点为H，画出图形，如图//AO平面11EBCFAO平面1AAMN，平面1AAMN平面11EBCFNP=//AONP又//NOAP6AONP==O为111ABC△的中心.1111sin606sin60333ONAC===

故：3ONAP==，则333AMAP==，平面11EBCF⊥平面1AAMN，平面11EBCF平面1AAMNNP=，MH平面1AAMNMH⊥平面11EBCF又在等边ABC中EFAPBCAM=即36233APBCEFAM

===由（1）知，四边形11EBCF为梯形四边形11EBCF的面积为：111126=62422EBCFEFBCSNP++==四边形111113BEBCFEBCFVSh−=四边形，h为M到PN的距离23sin603MH==，1243243V==.【点睛】本题主

要考查了证明线线平行和面面垂直，及其求四棱锥的体积，解题关键是掌握面面垂直转为求证线面垂直的证法和棱锥的体积公式，考查了分析能力和空间想象能力，属于中档题.21．（2020·全国·高考真题）如图，已知三棱柱

ABC-A1B1C1的底面是正三角形，侧面BB1C1C是矩形，M，N分别为BC，B1C1的中点，P为AM上一点，过B1C1和P的平面交AB于E，交AC于F.（1）证明：AA1∥MN，且平面A1AMN⊥EB1C1F；（2）设O为△A1B1C1的中心，若AO∥平面EB1C1F，且AO=AB，求直线B1

E与平面A1AMN所成角的正弦值.【答案】（1）证明见解析；（2）1010.【分析】（1）由,MN分别为BC，11BC的中点，1//MNCC，根据条件可得11//AABB，可证1MNAA//，要证平面11EBCF⊥平

面1AAMN，只需证明EF⊥平面1AAMN即可；（2）连接NP，先求证四边形ONPA是平行四边形，根据几何关系求得EP，在11BC截取1BQEP=，由（1）BC⊥平面1AAMN，可得QPN为1BE与平面1AAMN所成角，即可求得答案.【详解】（1）,MN分别为BC，11BC的中点，1/

/MNBB，又11//AABB，1//MNAA，在ABC中，M为BC中点，则BCAM⊥，又侧面11BBCC为矩形，1BCBB⊥，1//MNBB，MNBC⊥，由MNAMM=，,MNAM平面1AAMN，BC⊥平面1AAMN，又11//BCBC，且11BC

平面ABC，BC平面ABC，11//BC平面ABC，又11BC平面11EBCF，且平面11EBCF平面ABCEF=11//BCEF，//EFBC，又BC⊥平面1AAMN，EF⊥平面1AAMN，EF平面11EBC

F，平面11EBCF⊥平面1AAMN.(2)[方法一]：几何法如图，过O作11BC的平行线分别交1111,ABAC于点11,EF，联结11,,,AEAOAFNP，由于//AO平面11EBCF，11//EF平面11

EBCF，11=AOEFO，AO平面11AEF，11EF平面11AEF，所以平面11//AEF平面11EBCF．又因平面11AEF平面111=AABBAE，平面11EBCF平面111=AABBEB，所以11∥EBAE．因为111BCAN⊥，11BCMN⊥，1ANMNN=，所以11BC⊥面

1AANM．又因1111∥EFBC，所以11⊥EF面1AANM，所以1AE与平面1AANM所成的角为1EAO．令2AB=，则11=NB，由于O为111ABC△的中心，故112233==OENB．在1RtAEO

中，122,3===AOABOE，由勾股定理得22112103=+=AEAOOE．所以11110sin10==EOEAOAE．由于11∥EBAE，直线1BE与平面1AAMN所成角的正弦值也为1010．[方法二]【最优解】：几何法因为//AO平面11EFCB，平

面11EFCB平面1=AMNANP，所以∥AONP．因为//ONAP，所以四边形OAPN为平行四边形．由（Ⅰ）知EF⊥平面1AMNA，则EF为平面1AMNA的垂线．所以1BE在平面1AMNA的射影为NP．从而1BE与

NP所成角的正弦值即为所求．在梯形11EFCB中，设1EF=，过E作11EGBC⊥，垂足为G，则3==PNEG．在直角三角形1BEG中，1110sin1010==BEG．[方法三]：向量法由（Ⅰ）知，11BC⊥平面1AAMN，则11BC为平面1AA

MN的法向量．因为∥AO平面11EBCF，AO平面1AAMN，且平面1AAMN平面11EBCFPN=，所以//AOPN．由（Ⅰ）知11,=∥AAMNAAMN，即四边形APNO为平行四边形，则==AONPAB．因为O为正111ABC△的中心，故13==APONAM．由面面平行

的性质得111111,33=∥EFBCEFBC，所以四边形11EFCB为等腰梯形．由P，N为等腰梯形两底的中点，得11PNBC⊥，则11110,==++=PNBCEBEPPNNB111111111623+−=−BCPNBCPNBC．设直线1BE与平面1AAMN所成角为，ABa=，

则2111211121103sin1013===+aEBBCEBBCaaa．所以直线1BE与平面1AAMN所成角的正弦值1010．[方法四]：基底法不妨设2===AOABAC，以向量1,,AAABAC为基底，从而11,,AAABAAAC=，,3=A

BAC．1111123=++=+EBEAAAABABAA，BCACAB=−，则12103=EB，||2BC=．所以112()3=+−=EBBCABAAACAB2224333−=−AB

ACAB．由（Ⅰ）知BC⊥平面1AAMN，所以向量BC为平面1AAMN的法向量．设直线1BE与平面1AAMN所成角，则11110sincos,10||===EBBCEBBCEBBC．故直线1BE与平面1AAMN所成角的正弦值为10sin10

=．[方法五]：坐标法过O过底面ABC的垂线，垂足为Q，以Q为坐标原点建立如图所示空间直角坐标系，设OAM=，AO=AB=2，则()()131,,2sin,0,2cos,0,1,32cos,03BAB−−，所以11313,,0,,2cos,033333AEA

BE==−，所以12,2cos,2sin,3BE=−−−易得()1,0,0n=r为平面A1AMN的一个法向量，则直线B1E与平面A1AMN所成角的正弦值为1112103cos,10449nBEnBEnBE==

=+【整体点评】(2)方法一：几何法的核心在于找到线面角，本题中利用平行关系进行等价转化是解决问题的关键；方法二：等价转化是解决问题的关键，构造直角三角形是求解角度的正弦值的基本方法；方法三：利用向量法的核心是找到平面的法向量和直线的方向向量，然后利用向量法求解即可；

方法四：基底法是立体几何的重要思想，它是平面向量基本定理的延伸，其关键之处在于找到平面的法向量和直线的方向向量.方法五：空间坐标系法是立体几何的重要方法，它是平面向量的延伸，其关键之处在于利用空间坐标系确定位置，找到平面的法向量和直线的方向向量.22．（2019·江苏·高考真题）如图，在

直三棱柱ABC－A1B1C1中，D，E分别为BC，AC的中点，AB=BC．求证：（1）A1B1∥平面DEC1；（2）BE⊥C1E．【答案】（1）见解析；（2）见解析.【分析】(1)由题意结合几何体的空间结构特征和线面平行的判定定理即可证得题中的结

论；(2)由题意首先证得线面垂直，然后结合线面垂直证明线线垂直即可.【详解】（1）因为D，E分别为BC，AC的中点，所以ED∥AB.在直三棱柱ABC-A1B1C1中，AB∥A1B1，所以A1B1∥ED.又因为ED⊂平面DEC1，A1B1平面DEC1，所以A1B1∥平面DEC1.（2）因为AB

=BC，E为AC的中点，所以BE⊥AC.因为三棱柱ABC-A1B1C1是直棱柱，所以CC1⊥平面ABC.又因为BE⊂平面ABC，所以CC1⊥BE.因为C1C⊂平面A1ACC1，AC⊂平面A1ACC1，C1C∩AC=C，所以BE⊥平

面A1ACC1.因为C1E⊂平面A1ACC1，所以BE⊥C1E.【点睛】本题主要考查直线与直线、直线与平面、平面与平面的位置关系等基础知识，考查空间想象能力和推理论证能力.23．（2019·北京·高考真题）如

图，在四棱锥PABCD−中，PA⊥平面ABCD，底部ABCD为菱形，E为CD的中点.（Ⅰ）求证：BD⊥平面PAC；（Ⅱ）若∠ABC=60°，求证：平面PAB⊥平面PAE；（Ⅲ）棱PB上是否存在点F，使得CF∥平面PAE？说明理由.【答案】（Ⅰ）见解

析；（Ⅱ）见解析；（Ⅲ）见解析.【分析】(Ⅰ)由题意利用线面垂直的判定定理即可证得题中的结论；(Ⅱ)由几何体的空间结构特征首先证得线面垂直，然后利用面面垂直的判断定理可得面面垂直；(Ⅲ)由题意，利用平行四边形的性质和线面

平行的判定定理即可找到满足题意的点.【详解】（Ⅰ）证明：因为PA⊥平面ABCD,所以PABD⊥；因为底面ABCD是菱形，所以ACBD⊥;因为PAACA=,,PAAC平面PAC,所以BD⊥平面PAC.（Ⅱ）证明：因为底面ABCD是菱形且60ABC=，所以ACD为正三角形，所以A

ECD⊥,因为//ABCD,所以AEAB⊥；因为PA⊥平面ABCD，AE平面ABCD,所以AEPA⊥；因为PAABA=所以⊥AE平面PAB，AE平面PAE,所以平面PAB⊥平面PAE.（Ⅲ）存在点F为PB中点时，满足//CF平面PAE；理由如下:分别取,PBPA的中点,FG，连接,,CFFGE

G,在三角形PAB中，//FGAB且12FGAB=；在菱形ABCD中，E为CD中点，所以//CEAB且12CEAB=，所以//CEFG且CEFG=，即四边形CEGF为平行四边形，所以//CFEG;又CF

平面PAE，EG平面PAE，所以//CF平面PAE.【点睛】本题主要考查线面垂直的判定定理，面面垂直的判定定理，立体几何中的探索问题等知识，意在考查学生的转化能力和计算求解能力.24．（2019·北

京·高考真题）如图，在四棱锥P–ABCD中，PA⊥平面ABCD，AD⊥CD，AD∥BC，PA=AD=CD=2，BC=3．E为PD的中点，点F在PC上，且13PFPC=．（Ⅰ）求证：CD⊥平面PAD；（Ⅱ）求二面角F–AE–P的余弦值；（

Ⅲ）设点G在PB上，且23PGPB=．判断直线AG是否在平面AEF内，说明理由．【答案】(Ⅰ)见解析；(Ⅱ)33；(Ⅲ)见解析.【分析】(Ⅰ)由题意利用线面垂直的判定定理即可证得题中的结论；(Ⅱ)建立空间直角坐标

系，结合两个半平面的法向量即可求得二面角F-AE-P的余弦值；(Ⅲ)首先求得点G的坐标，然后结合平面AEF的法向量和直线AG的方向向量可判断直线是否在平面内.【详解】(Ⅰ)由于PA⊥平面ABCD，CD平面ABCD，则PA⊥CD，由题意可知AD⊥C

D，且PA∩AD=A，由线面垂直的判定定理可得CD⊥平面PAD.(Ⅱ)以点A为坐标原点，平面ABCD内与AD垂直的直线为x轴，AD,AP方向为y轴，z轴建立如图所示的空间直角坐标系Axyz−，易知：()()()()0,0,0,0,0,2,2,2,0,0,2,0APCD，由13PFP

C=可得点F的坐标为224,,333F，由12PEPD=可得()0,1,1E，设平面AEF的法向量为：(),,mxyz=，则()()()224224,,,,0333333,,0,1,10mAFxyzxyzmAExyzyz

==++===+=，据此可得平面AEF的一个法向量为：()1,1,1m=−，很明显平面AEP的一个法向量为()1,0,0n=r，13cos,331mnmnmn===，二面角F-AE-P的平

面角为锐角，故二面角F-AE-P的余弦值为33.(Ⅲ)易知()()0,0,2,2,1,0PB−，由23PGPB=可得422,,333G−，则422,,333AG=−，注意到平面AEF的一个法向量为：

()1,1,1m=−，其0mAG=且点A在平面AEF内，故直线AG在平面AEF内.25．（2019·全国·高考真题）图1是由矩形,ADEBRtABC和菱形BFGC组成的一个平面图形，其中1,2ABBEBF===，60FBC=，将其沿,ABBC

折起使得BE与BF重合，连结DG，如图2.（1）证明图2中的,,,ACGD四点共面，且平面ABC⊥平面BCGE；（2）求图2中的四边形ACGD的面积.【答案】(1)见详解；(2)4.【分析】(1)因为折纸和粘合不改变矩形ABED，Rt

ABC和菱形BFGC内部的夹角，所以//ADBE，//BFCG依然成立，又因E和F粘在一起，所以得证.因为AB是平面BCGE垂线，所以易证.(2)欲求四边形ACGD的面积，需求出CG所对应的高，然后乘以CG即可．【详解】(1

)证：//ADBE，//BFCG，又因为E和F粘在一起.//ADCG，A，C，G，D四点共面.又,ABBEABBC⊥⊥.AB⊥平面BCGE，AB平面ABC，平面ABC⊥平面BCGE，得证.(2)取

CG的中点M，连结,EMDM.因为//ABDE，AB⊥平面BCGE，所以DE⊥平面BCGE，故DECG⊥，由已知，四边形BCGE是菱形，且60EBC=得EMCG⊥，故CG⊥平面DEM．因此DMCG⊥．在RtDEM△中，DE=1，3EM=，故2DM=．所以四边形ACGD的面积为4.【点睛

】很新颖的立体几何考题．首先是多面体粘合问题，考查考生在粘合过程中哪些量是不变的．再者粘合后的多面体不是直棱柱，最后将求四边形ACGD的面积考查考生的空间想象能力.26．（2019·全国·高考真题）图1是由矩形ADEB，Rt△AB

C和菱形BFGC组成的一个平面图形，其中AB=1，BE=BF=2，∠FBC=60°，将其沿AB，BC折起使得BE与BF重合，连结DG，如图2.（1）证明：图2中的A，C，G，D四点共面，且平面ABC⊥平面BCGE；（2）求图2中的二面角B−CG−A的大小.【答案】(1)见详解；(2

)30.【分析】(1)因为折纸和粘合不改变矩形ABED，RtABC和菱形BFGC内部的夹角，所以//ADBE，//BFCG依然成立，又因E和F粘在一起，所以得证.因为AB是平面BCGE垂线，所以易证.(2)在图中找到BCGA−−对应的平面角，再求此平面角即可.于是考虑B关于GC的垂线，发现

此垂足与A的连线也垂直于CG.按照此思路即证.【详解】(1)证：//ADBE，//BFCG，又因为E和F粘在一起.//ADCG，A，C，G，D四点共面.又,ABBEABBC⊥⊥.AB⊥平面BCGE，AB平面ABC，平面ABC⊥平面BCGE，得证.(2)过B作BHGC⊥延长线于H，连结AH

，因为AB⊥平面BCGE，所以ABGC⊥而又BHGC⊥，故GC⊥平面HAB，所以AHGC⊥.又因为BHGC⊥所以BHA是二面角BCGA−−的平面角，而在BHC△中90BHC=，又因为60FBC=故60BCH=，所以s

in603BHBC==.而在ABH中90ABH=,13tan33ABBHABH===，即二面角BCGA−−的度数为30.【点睛】很新颖的立体几何考题．首先是多面体粘合问题，考查考生在粘合过程中哪些量是不变的．再者粘合后的多面体不是直棱柱，建系的向量解法在本题中略显麻烦，突

出考查几何方法．最后将求二面角转化为求二面角的平面角问题考查考生的空间想象能力．27．（2019·天津·高考真题）如图，在四棱锥PABCD−中，底面ABCD为平行四边形，PCD为等边三角形，平面PAC⊥平面PCD，PACD⊥，2CD=，3AD=，（Ⅰ）设GH，分别为PBAC，的中点，求证：GH平面

PAD；（Ⅱ）求证：PA⊥平面PCD；（Ⅲ）求直线AD与平面PAC所成角的正弦值.【答案】（I）见解析；（II）见解析；（III）33.【分析】（I）连接BD，结合平行四边形的性质，以及三角形中位线的性质，得到GHPD，利用线面平行的判定定理证得结果；（II）取棱PC

的中点N，连接DN，依题意，得DNPC⊥，结合面面垂直的性质以及线面垂直的性质得到DNPA⊥，利用线面垂直的判定定理证得结果；（III）利用线面角的平面角的定义得到DAN为直线AD与平面PAC所成的角，放在直角三角形中求得结果.【详解】（I）证明：连接BD，易知ACBDH=，BHDH

=，又由BG=PG，故GHPD，又因为GH平面PAD，PD平面PAD，所以GH平面PAD.（II）证明：取棱PC的中点N，连接DN，依题意，得DNPC⊥，又因为平面PAC⊥平面PCD，平面PAC平面PCDPC=，所以DN⊥平面PAC，又PA平面PAC，故DNP

A⊥，又已知PACD⊥，CDDND=，所以PA⊥平面PCD.（III）解：连接AN，由（II）中DN⊥平面PAC，可知DAN为直线AD与平面PAC所成的角.因为PCD为等边三角形，2CD=且N为PC的中点，所以3DN=，又DNAN⊥，在RtAND中，3si

n3DNDANAD==，所以，直线AD与平面PAC所成角的正弦值为33.【点睛】本小题主要考查直线与平面平行、直线与平面垂直、平面与平面垂直、直线与平面所成的角等基础知识，考查空间想象能力和推理能力.28．（2019·浙江·高考真题）如图，已知三棱柱111ABCABC-，平面11AACC

⊥平面ABC,90ABC=，1130,,,BACAAACACEF===分别是11,ACAB的中点.（1）证明：EFBC⊥；（2）求直线EF与平面1ABC所成角的余弦值.【答案】（1）证明见解析；（2）35.【分析】(1)由题意首先证得线面垂

直，然后利用线面垂直的定义即可证得线线垂直；(2)建立空间直角坐标系，分别求得直线的方向向量和平面的法向量，然后结合线面角的正弦值和同角三角函数基本关系可得线面角的余弦值.【详解】(1)如图所示，连结11,AEBE，等边1AAC△中，AEEC=，则1AEAC⊥，平

面ABC⊥平面11AACC，且平面ABC∩平面11AACCAC=，由面面垂直的性质定理可得：1AE⊥平面ABC，故1AEBC⊥，由三棱柱的性质可知11ABAB∥，而ABBC⊥，故11ABBC⊥，且1111ABAEA=，由线面垂直的判定定理可得：BC⊥平面11

ABE，结合EF⊆平面11ABE，故EFBC⊥.(2)在底面ABC内作EH⊥AC，以点E为坐标原点，EH,EC,1EA方向分别为x,y,z轴正方向建立空间直角坐标系Exyz−.设1EH=，则3AEEC==，1123AACA==,3,3BCAB==，据

此可得：()()()1330,3,0,,,0,0,0,3,0,3,022ABAC−，由11ABAB=可得点1B的坐标为133,3,322B，利用中点坐标公式可得：33,3,344F，由于()0,0,0E，故直线EF的方向向量为：33,3,3

44EF=设平面1ABC的法向量为(),,mxyz=，则：()()13333,,,,33022223333,,,,002222mABxyzxyzmBCxyzxy=−=+−==−=−+=，据此可得平面1ABC的一个法向量为

()1,3,1m=，33,3,344EF=此时64cos,53552EFmEFmEFm===，设直线EF与平面1ABC所成角为，则43sincos,,cos55EFm===.【点睛】本题考查了立体几何中的线线垂

直的判定和线面角的求解问题，意在考查学生的空间想象能力和逻辑推理能力；解答本题关键在于能利用直线与直线、直线与平面、平面与平面关系的相互转化，通过严密推理，同时对于立体几何中角的计算问题，往往可以利用空间向量法，通过求解平面的法向量，利用向量的夹角公式求解.29．（

2019·全国·高考真题）如图，长方体ABCD–A1B1C1D1的底面ABCD是正方形，点E在棱AA1上，BE⊥EC1.（1）证明：BE⊥平面EB1C1；（2）若AE=A1E，AB=3，求四棱锥11EBBCC−的体积．【答案】（1）见详解；（2）18【

分析】（1）先由长方体得，11BC⊥平面11AABB，得到11BCBE⊥，再由1BEEC⊥，根据线面垂直的判定定理，即可证明结论成立；（2）先设长方体侧棱长为2a，根据题中条件求出3a=；再取1BB中点F，连结EF，证明EF⊥平面11BBCC，根据四棱锥的体积公式，即可求出结果.

【详解】（1）因为在长方体1111ABCDABCD−中，11BC⊥平面11AABB；BE平面11AABB，所以11BCBE⊥，又1BEEC⊥，1111BCECC=，且1EC平面11EBC，11BC平面11

EBC，所以BE⊥平面11EBC；（2）[方法一]【利用体积公式计算体积】如图6，设长方体的侧棱长为2a，则1AEAEa==．由（1）可得1EBBE⊥．所以22211EBBEBB+=，即2212BEBB=．又3AB

=，所以222122AEABBB+=，即222184aa+=，解得3a=．取1BB中点F，联结EF，因为1AEAE=，则EFAB∥，所以EF⊥平面11BBCC，从而四棱锥11EBBCC−的体积：11111133EBBCCBBCCVSEFBC

BB−==矩形1363183EF==．[方法二]【最优解：利用不同几何体之间体积的比例关系计算体积】取1BB的中点F，联结EF．由（Ⅰ）可知1BEEB⊥，所以1113,62EFBBABBB====．故11113361833EBBCCVV−===长

方体．【整体点评】(2)方法一：利用体积公式计算体积需要同时计算底面积和高，是计算体积的传统方法；方法二：利用不同几何体之间的比例关系计算体积是一种方便有效快速的计算体积的方法，核心思想为等价转化.30．（2019·全国·高考真题）如图，长方体ABCD–A1B1C

1D1的底面ABCD是正方形，点E在棱AA1上，BE⊥EC1.（1）证明：BE⊥平面EB1C1；（2）若AE=A1E，求二面角B–EC–C1的正弦值.【答案】（1）证明见解析；（2）32【分析】（1）利用长方体的性质，可以知道11BC⊥侧面11ABBA，利用线面垂直的性质可以证明出11BCEB⊥

，这样可以利用线面垂直的判定定理，证明出BE⊥平面11EBC；（2）以点B坐标原点，以1,,BCBABB分别为,,xyz轴，建立空间直角坐标系，设正方形ABCD的边长为a，1BBb=，求出相应点的坐标，利用1BEEC⊥，可以求出,ab之间的关系，分别求出平面EBC、平面1ECC的法向量，利用空间向

量的数量积公式求出二面角1BECC−−的余弦值的绝对值，最后利用同角的三角函数关系，求出二面角1BECC−−的正弦值.【详解】（1）证明：因为1111ABCDABCD−是长方体，所以11BC⊥侧面11ABBA，而BE平面11A

BBA，所以11BEBC⊥又1BEEC⊥，1111BCECC=，111,BCEC平面11EBC，因此BE⊥平面11EBC；（2）[方法一]【三垂线定理】由（1）知，1BEEB⊥，又E为1AA的中点，所以1B

EB，为等腰直角三角形，所以12AAAB=．如图2，联结AC，与BD相交于点O，因为1AA⊥平面ABCD，所以1AABO⊥．又BOAC⊥，所以BO⊥平面11ACCA．作OHCE⊥，垂足为H，联结BH，由三垂线定理可知BHCE⊥，则OHB为二面角1

BECC−−平面角的补角．设1AB=，则12,1,2,3AAAEACCE====，由OHAEOCCE=，得66OH=．在RtBOH中，2263BHOHOB=+=，所以3sin2OBOHBBH==，即二面角1BECC−−的正弦值为32．[方法二]【利用平面的法向量】设底面边长

为1，高为2x，所以222211,1BExBEx=+=+．因为BE⊥平面11EBC，所以190BEB=，即22211BEBEBB+=，所以22224xx+=，解得1x=．因为BC⊥平面11AABB，所以1BCBE⊥，又1BEBE⊥，所以1BE⊥平面BCE，故1BE为平面BCE的一个法向量

．因为平面1CCE与平面11AACC为同一平面，故11BD为平面1CCE的一个法向量，在11BDE中，因为11112BDDEBE===，故1BE与11BD成60角，所以二面角1BECC−−，的正弦值为3sin602=．[

方法三]【利用体积公式结合二面角的定义】设底面边长为1，高为2x，所以222211,1BExBEx=+=+．因为BE⊥平面11EBC，所以190BEB=，即22211BEBEBB+=，所以22224x

x+=，解得1x=．因为BCBE⊥，所以BCE是直角三角形，1,3,2BCECEB===．因为1BB∥平面1ECC，所以1,BB到平面1ECC的距离相等设为1h．同理，A，E到平面11BBC的距离相等

，都为1，所以1111EBBCBECCVV−−=，即11111133BBCBCCSABSh=VV，解得122h=．设点B到直线CE的距离为2h，在BCE中，由面积相等解得263h=．设为二面角1BECC−−的平面角，123sin2hh==，所以二面角1BECC−

−的正弦值为32．[方法四]【等价转化后利用射影面积计算】由（1）的结论知1BEEB⊥，又1AEAE=，易证11ABEABE≌，所以1145AEBAEB==，所以AEAB=，即二面角1BECC−

−的正弦值与二面角BECA−−的正弦值相等．设111,,BBCCDD的中点分别为F，G，H，显然ABCDEFGH−为正方体，所求问题转化为如图3所示，在正方体ABCDEFGH−中求二面角BECA−−的正弦值．设,ACBD相交于点O，易证BO⊥平面ACGE，所以EOC△是EBC在平面ACGE上的射

影．令正方体ABCDEFGH−的棱长2ABBCAE===，则22BE=，2OC=，122BDCSOCAE==V，1222EBCSBCBE==V．设二面角BECA−−为，由cosBDCEBCSS=VV，

则21cos222BDCEBCSS===VV，所以3sin2=．即二面角1BECC−−的正弦值为32．[方法五]【结合（1）的结论找到二面角的平面角进行计算】如图4，分别取111,,BBCCDD中点F，G，H，联结,,,EFFGGHGE．过G作GPEC⊥，垂足为P，联

结BP．易得E，F，G，H共面且平行于面ABCD．由（1）可得BE⊥面11EBC．因为1BE面11EBC，所以1BEBE⊥．又因为E为1AA中点，所以11ABEABE≌，且均为等腰三角形．设1AB=，则1AE=，四棱柱A

BCDEFGH−为正方体．在GEC及BEC中有1,2,3CGCBEGEBEC=====．所以EGCV与BEC均为直角三角形且全等．又因为GPEC⊥，所以,BPECBPG⊥为二面角BECG−−（即1BECC−−）的一个平面角．在BPG中，2,23G

PBPBG===．所以222222133cos2222233BPGPGBBPGBPGP+−+−===−，所以3sin2BPG=．故二面角1BECC−−的正弦值为32．[方法六]【最优解：空间向量法】以点B坐标原点，以1,,BCBABB分别为,,xyz轴，建立如下图所示的

空间直角坐标系，1(0,0,0),(,0,0),(,0,),(0,,)2bBCaCabEa，因为1BEEC⊥，所以2210(0,,)(,,)002224bbbBEECaaaaba=−=−+==，所以(0,,)Eaa，1(

,,),(0,0,2),(0,,)ECaaaCCaBEaa=−−==，设111(,,)mxyz=是平面BEC的法向量，所以111110,0,(0,1,1)0.0,ayazmBEmaxayazmEC+==

=−−−==，设222(,,)nxyz=是平面1ECC的法向量，所以2122220,0,(1,1,0)0.0,aznCCnaxayaznCE===−−==，二面角1BECC−−的余弦值的绝对值为11222mnmn=

=，所以二面角1BECC−−的正弦值为2131()22−=.【整体点评】(2)方法一：三垂线定理是立体几何中寻找垂直关系的核心定理；方法二：利用平面的法向量进行计算体现了等价转化的数学思想，是垂直关系的进一步应用；方法三：体积公式可以计算点面距离，结合点面距离可进一步计算二面角

的三角函数值；方法四：射影面积法体现等价转化的数学思想，是将角度问题转化为面积问题的一种方法；方法五：利用第一问的结论找到二面角，然后计算其三角函数值是一种常规的思想；方法六：空间向量是处理立体几何的常规方法，在二面角不好寻找的时候利用空间向量是一种更好的方法.31．（2018·江苏·高考真题）在

平行六面体1111ABCDABCD−中，1AAAB=,111ABBC⊥．求证：（1）11//ABABC平面；（2）111ABBAABC⊥平面平面．【答案】（1）见解析（2）见解析【详解】分析：（1）先根据平行六面体得线线平行，再根据线面平行判定

定理得结论；（2）先根据条件得菱形ABB1A1，再根据菱形对角线相互垂直，以及已知垂直条件，利用线面垂直判定定理得线面垂直，最后根据面面垂直判定定理得结论.详解：证明：（1）在平行六面体ABCD-A1B1C1D1中，AB∥A1B1．因为AB平面A1B1C，A

1B1平面A1B1C，所以AB∥平面A1B1C．（2）在平行六面体ABCD-A1B1C1D1中，四边形ABB1A1为平行四边形．又因为AA1=AB，所以四边形ABB1A1为菱形，因此AB1⊥A1B．又因为AB1⊥B1C1，BC∥B1C1，所以AB1⊥BC．又因为A1B∩BC=B

，A1B平面A1BC，BC平面A1BC，所以AB1⊥平面A1BC．因为AB1平面ABB1A1，所以平面ABB1A1⊥平面A1BC．点睛：本题可能会出现对常见几何体的结构不熟悉导致几何体中的位置关系无

法得到运用或者运用错误，如柱体的概念中包含“两个底面是全等的多边形，且对应边互相平行，侧面都是平行四边形”，再如菱形对角线互相垂直的条件，这些条件在解题中都是已知条件，缺少对这些条件的应用可导致无法证明.32．（20

18·北京·高考真题）如图，在三棱柱ABC−111ABC中，1CC⊥平面ABC，D，E，F，G分别为1AA，AC，11AC，1BB的中点，AB=BC=5，AC=1AA=2．（1）求证：AC⊥平面BEF；

（2）求二面角B−CD−C1的余弦值；（3）证明：直线FG与平面BCD相交．【答案】（1）证明见解析；（2）2121−；（3）证明见解析．【分析】（1）由等腰三角形性质得ACBE⊥，由线面垂直性质得1ACCC⊥,由三棱柱性质可得1//EFCC

，因此EFAC⊥，最后根据线面垂直判定定理得结论；（2）根据条件建立空间直角坐标系，设各点坐标，利用方程组解得平面BCD一个法向量，根据向量数量积求得两法向量夹角，再根据二面角与法向量夹角相等或互补关系求结果；（3）根据平面BCD一个法向量与直线

FG方向向量数量积不为零，可得结论.【详解】（1）在三棱柱ABC-A1B1C1中，∵CC1⊥平面ABC，∴四边形A1ACC1为矩形．又E，F分别为AC，A1C1的中点，∴AC⊥EF．∵AB=BC，E为AC的中点，

．∴AC⊥BE，而BEEFB=，∴AC⊥平面BEF．（2）［方法一］：【通性通法】向量法由（1）知AC⊥EF，AC⊥BE，EF∥CC1．又CC1⊥平面ABC，∴EF⊥平面ABC．∵BE平面ABC，∴EF⊥BE．如图建立空间直角坐称系E-xyz．由题意得B（0，2，0），C（-1，0，0），D（1

，0，1），F（0，0，2），G（0，2，1）．∴()()=201=120CDCB，，，，，，设平面BCD的法向量为()nabc=，，，∴00nCDnCB==，∴2020acab+=+

=，令a=2，则b=-1，c=-4，∴平面BCD的一个法向量()214n=−−，，，又∵平面CDC1的一个法向量为()=020EB，，，∴21cos=21EBEBEnBnn=−．由图可得二面角B-CD-C1为钝角，所以二面角B-CD-

C1的余弦值为2121−．［方法二］：【最优解】转化＋面积射影法考虑到二面角BCDA−−与二面角1BCDC--互补，设二面角1BCDC--为，易知5DC=，6DB=，所以121,22DCEDCBSS==△△．故1212cos21212DCEDC

BSS=−=−=−△△．［方法三］：转化＋三垂线法二面角BCDA−−与二面角1BCDC--互补，并设二面角BCDA−−为，易知BE⊥平面ACD．如图3，作EHCD⊥，垂足为H，联结BH．则BHE是二面角BCDA−−的平面角，所以BHE=，不难求出21cos21=，所以二面角1

BCDC--的余弦值为2121−．（3）［方法一］：【最优解】【通性通法】向量法平面BCD的一个法向量为()214n=−−，，，∵G（0，2，1），F（0，0，2），∴()=021GF−，，，∴2nGF=−，∴n与GF不垂直，∴GF与平面B

CD不平行且不在平面BCD内，∴GF与平面BCD相交．［方法二］：几何转化如图4，取11AB的中点G，分别在11,BBCC取点N，M，使11114,4BNBBCMCC==．联结,,,FGGNNMFM．则平面DCB∥

平面FGNM，又FM平面FGNM，FG平面FGNM，故直线FG与平面BCD相交．［方法三］：根据相交的平面定义如图5，设CD与EF交于P，联结PB．因为1EFBB，且1EFBB=，所以1,,,BEFB四点共面．因为131,42PFEFBGBB==，所以PFBG．又PFBG∥，所以四

边形PFGB是梯形，即直线FG与直线BP一定相交．因为BP平面BCD，所以直线FG与平面BCD相交．【整体点评】（2）方法一：直接利用向量法求出，属于通性通法；方法二：根据二面角BCDA−−与二面角1BCDC--互补，通过转化求二面角BCDA−−，利用面积射影

法求出，是该问的最优解；方法三：根据二面角BCDA−−与二面角1BCDC--互补，通过转化求二面角BCDA−−，利用三垂线法求出；（3）方法一：利用向量证明平面的法向量与直线的方向向量不垂直即可，既是该问的通性通法，也是最优解；方

法二：通过证明与平面BCD平行的平面与直线FG相交证出；方法三：构建过直线FG且与平面BCD相交的平面，通过证明直线FG与交线相交证出．33．（2018·北京·高考真题）如图，在四棱锥PABCD−中，底面ABCD为矩形，平面

PAD⊥平面ABCD，PAPD⊥，PAPD=，E、F分别为AD、PB的中点.（Ⅰ）求证：PEBC⊥；（Ⅱ）求证：平面PAB⊥平面PCD；（Ⅲ）求证：//EF平面PCD.【答案】（Ⅰ）见解析；（Ⅱ）见解析；（Ⅲ）见解析.【分析】（1）欲证PEBC⊥，只需证明PEAD⊥即可；（2）先证PD⊥平面P

AB，再证平面PAB⊥平面PCD；（3）取PC中点G，连接,FGDG，证明//EFDG，则//EF平面PCD.【详解】（Ⅰ）∵PAPD=，且E为AD的中点，∴PEAD⊥.∵底面ABCD为矩形，∴//BCAD，∴PEBC⊥；（Ⅱ）∵底面ABCD为矩形，∴ABAD⊥.∵平面PAD⊥

平面ABCD，平面PAD平面ABCDAD=，AB平面ABCD，∴AB⊥平面PAD，又PD平面PAD，∴ABPD⊥.又PAPD⊥，PAABA=，PA、AB平面PAB，PD⊥平面PAB，∵PD平面PCD，∴平面PAB⊥平面PCD

；（Ⅲ）如图，取PC中点G，连接,FGGD.∵,FG分别为PB和PC的中点，∴//FGBC，且12FGBC=.∵四边形ABCD为矩形，且E为AD的中点，∴1//,2EDBCDEBC=，∴//EDFG，且EDFG=，∴四边

形EFGD为平行四边形，∴//EFGD，又EF平面PCD，GD平面PCD，∴//EF平面PCD.【点睛】证明面面关系的核心是证明线面关系，证明线面关系的核心是证明线线关系.证明线线平行的方法：（1）线面平行的性质定理；（2）三角形中位线法；（3）平行四边形法.证明线线

垂直的常用方法：（1）等腰三角形三线合一；（2）勾股定理逆定理；（3）线面垂直的性质定理；（4）菱形对角线互相垂直.34．（2018·全国·高考真题）如图，边长为2的正方形ABCD所在的平面与半圆弧CD所在平面垂

直，M是CD上异于C，D的点．（1）证明：平面AMD⊥平面BMC；（2）当三棱锥MABC−体积最大时，求面MAB与面MCD所成二面角的正弦值．【答案】（1）证明见解析；（2）255．【分析】（1）方法一：先证BC⊥平面CMD,得BCDM⊥,再证CMDM⊥，由线面垂直的判定定理可得DM⊥平面BM

C，即可根据面面垂直的判定定理证出；（2）方法一：先建立空间直角坐标系，然后判断出M的位置，求出平面MAB和平面MCD的法向量，进而求得平面MAB与平面MCD所成二面角的正弦值．【详解】（1）［方法一］：【最优解】判定定理由题设知,平面

CMD⊥平面ABCD,交线为CD.因为BC⊥CD,BC平面ABCD,所以BC⊥平面CMD,故BC⊥DM.因为M为CD上异于C，D的点,且DC为直径，所以DM⊥CM.又BCCM=C,所以DM⊥平面BMC.而DM平面AMD,故平面AMD⊥平面BMC.［方法二］：判定

定理由题设知,平面CMD⊥平面ABCD,交线为CD.因为ADCD⊥，AD平面ABCD,所以AD⊥平面MCD，而CM平面MCD，所以AD⊥CM，因为M为CD上异于C，D的点,且DC为直径，所以DM⊥CM.又ADD

MD=，所以，CM⊥平面AMD，而CM平面BMC，所以平面AMD⊥平面BMC．［方法三］：向量法建立直角坐标系，如图2，设(0,,)Mab，()()()()0,0,0,2,0,0,2,2,0,0,2

,0,DABC所以()()2,0,0,0,,DADMab==，设平面AMD的一个法向量为()111,,mxyz=，所以=0=0nDAnDM，即1112=0+=0xaybz，取平面AMD的一个

法向量(0,,)mba=−，同理可得，平面BMC的一个法向量(0,,2)nba=−，因为点M在以()0,1,0为圆心，半径为1的圆上，所以，()2211ab−+=，即2220aba+−=，而2220banam+=−=，所以平面AMD⊥平面BMC．（2）

［方法一］：【通性通法】向量法以D为坐标原点,DA的方向为x轴正方向,建立如图所示的空间直角坐标系D−xyz.当三棱锥M−ABC体积最大时，M为CD的中点.由题设得()()()()()0,0,0,2,0,0,2,2,0,0,2,0,0,1,1DABCM，()()()2,1,1,0,

2,0,2,0,0AMABDA=−==设(),,nxyz=是平面MAB的法向量,则=0=0nAMnAB即2++=02=0xyzy−，可取()1,0,2n=.DA是平面MCD的一个法向量,

因此5cos,5DADDAnAnn==，25sin,5nDA=，所以面MAB与面MCD所成二面角的正弦值是255.［方法二］：几何法（作平行线找公共棱）如图3，当点M与圆心O连线MODC⊥时，三棱锥MABC−体积最大．过点M作,,

EFDCEDDCFCDC⊥⊥∥，易证BFC为所求二面角的平面角．在RtBCF△中，25sin5BCBFCBF==，即面MAB与面MCD所成二面角的正弦值是255．［方法三］：【最优解】面积射影法设平面MAB与平面MCD

所成二面角的平面角为．由题可得MAB△在MCD△平面上的射影图形正好是MCD△．取AB和CD的中点分别为N和O，则可得1OM=，5MN=，所以由射影面积公式有1cos5MCDMABSS==△△，所以25

sin5=，即面MAB与面MCD所成二面角的正弦值是255．［方法四］：定义法如图4，可知平面MAB与平面MCD的交线l过点M，可以证明,lABlCD∥∥．分别取,CDAB的中点O，E，联结,,OEMOME，可证得直线CD⊥平面OME，于是l⊥平面OME，所以,

lMOlME⊥⊥，故OME是面MAB与面MCD所成二面角的平面角．在OME△中，,1,2MOOEMOOE⊥==，则5ME=，所以25sin5OME=，即面MAB与面MCD所成二面角的正弦值为255．【整体点评】（1）方法一：利用面面垂直的判定定理寻找合适的线面垂直即可证出，是本题的最

优解；方法二：同方法一，只不过找的线面垂直不一样；方法三：利用向量法，计算两个平面的法向量垂直即可，思路简单，运算较繁．（2）方法一：直接利用向量法解决无棱二面角问题，是该类型题的通性通法；方法二：作平行线找公共棱，从而利用

二面角定义找到二面角的平面角，是传统解决无棱二面角问题的方式；方法三：面积射影法也是传统解决无棱二面角问题的方式，是本题的最优解；方法四：同方法二，通过找到二面角的公共棱，再利用定义找到平面角，即可解出．35．（2018·浙江·高考真题）如图，已知多面体111111,,,ABCABCAABB

CC−均垂直于平面111,120,4,1,2ABCABCAACCABBCBB======．（Ⅰ）求证：1AB⊥平面111ABC；（Ⅱ）求直线1AC与平面1ABB所成角的正弦值．【答案】（Ⅰ）证明见解析；（Ⅱ）3913.【分析】（Ⅰ）方法一：通过计算，根据勾股定理得111111,ABA

BABBC⊥⊥,再根据线面垂直的判定定理得结论；（Ⅱ）方法一：找出直线AC1与平面ABB1所成的角，再在直角三角形中求解即可.【详解】（Ⅰ）［方法一］：几何法由11112,4,2,,ABAABBAAABBBAB===⊥⊥得11122ABAB==，所以2221111ABABAA+

=，即有111ABAB⊥.由2BC=，112,1,BBCC==11,BBBCCCBC⊥⊥得115BC=，由2,120ABBCABC===得23AC=，由1CCAC⊥，得113AC=，所以2221111ABBCAC+=，即有111ABBC⊥，又11111ABBCB=，因此1A

B⊥平面111ABC.［方法二］：向量法如图，以AC的中点O为原点，分别以射线OB，OC为x，y轴的正半轴，建立空间直角坐标系O-xyz.由题意知各点坐标如下：()()()()()1110,3,0,1,0,0,0,3,4,1,0

,2,0,3,1,ABABC−−因此11111(1,3,2),(1,3,2),(0,23,3)ABABAC==−=−,由1110ABAB=得111ABAB⊥；由1110ABAC=得111ABAC⊥，所以

1AB⊥平面111ABC.（Ⅱ）［方法一］：定义法如图，过点1C作111CDAB⊥，交直线11AB于点D，连结AD.由1AB⊥平面111ABC得平面111ABC⊥平面1ABB，由111CDAB⊥得1CD⊥平面1ABB，所以1CAD是1AC与平面1ABB所成的角.由1111115,

22,21BCABAC===得11111161cos,sin77CABCAB==，所以13CD=，故11139sin13CDCADAC==.因此，直线1AC与平面1ABB所成的角的正弦值是3913.［方法二］：向量法设直线

1AC与平面1ABB所成的角为.由(I)可知11(0,23,1),(1,3,0),(0,0,2)ACABBB===,设平面1ABB的法向量(,,)nxyz=.由100nABnBB==即3020xyz+==，可取(3,1,0)n=−，

所以11139sincos,13||ACnACnACn===.因此，直线1AC与平面1ABB所成的角的正弦值是3913.［方法三］：【最优解】定义法+等积法设直线1AC与平面1ABB所成角为，点1C到平面1ABB距离为d（下同）．因为1CC∥平面1ABB，所

以点C到平面1ABB的距离等于点1C到平面1ABB的距离．由条件易得，点C到平面1ABB的距离等于点C到直线AB的距离，而点C到直线AB的距离为3，所以3d=．故1339sin1313dAC===．［方法四］：定义法+等积法设直线1AC

与平面1ABB所成的角为，由条件易得11111122,5,21ABBCAC===，所以222111111111111110cos25ABBCACABCABBC+−==−，因此11115sin5ABC=．于是得11111111111sin62ABCSABBCABC==△，

易得114AABS=△．由111111CAABAABCVV−−=得1111111133AABABCSdSAB=△△，解得3d=．故1339sin1313dAC===．［方法五］：三正弦定理的应用设直线1AC与平面

1ABB所成的角为，易知二面角11CAAB−−的平面角为6BAC=，易得1123sin13CAA=，所以由三正弦定理得1123139sinsinsin21313CAABAC===．［方法六］：三余弦定理的应用设直线1AC与平面1ABB所成的角为，如图2，过点C作CGAB⊥，垂足

为G，易得CG⊥平面1ABB，所以CG可看作平面1ABB的一个法向量．结合三余弦定理得1123339sincos,coscos131323ACCGCACGCA====．［方法七］：转化法＋定义法如图3，延长线段1AA至E，使得1AECC=．联结

CE，易得1ECAC∥，所以1AC与平面1ABB所成角等于直线EC与平面1ABB所成角．过点C作CGAB⊥，垂足为G，联结GE，易得CG⊥平面1ABB，因此EG为EC在平面1ABB上的射影，所以CEG为直线EC与平面1ABB所成的角．易得13CE=，3CG=，因此339sin1313CGCEG

CE===．［方法八］：定义法＋等积法如图4，延长11,ABAB交于点E，易知2BE=，又2ABBC==，所以ACCE⊥，故CE⊥面11AACC．设点1C到平面1ABB的距离为h，由1111EAACCAAEVV−−=得1111113232AAAEhA

AACCE=，解得3h=．又113AC=，设直线1AC与平面1ABB所成角为，所以339sin1313==．【整体点评】（Ⅰ）方法一：通过线面垂直的判定定理证出，是该题的通性通法；方法

二：通过建系，根据数量积为零，证出；（Ⅱ）方法一：根据线面角的定义以及几何法求线面角的步骤，“一作二证三计算”解出；方法二：根据线面角的向量公式求出；方法三：根据线面角的定义以及计算公式，由等积法求出点面距，即可求出

，该法是本题的最优解；方法四：基本解题思想同方法三，只是求点面距的方式不同；方法五：直接利用三正弦定理求出；方法六：直接利用三余弦定理求出；方法七：通过直线平移，利用等价转化思想和线面角的定义解出；方法八：通过等价转化以及线面角的定义，计算公式

，由等积法求出点面距，即求出．36．（2018·全国·高考真题）如图，在三棱锥PABC−中，22ABBC==，4PAPBPCAC====，O为AC的中点．（1）证明：PO⊥平面ABC；（2）若点M在棱BC上，且2MCMB=，求点C到平面POM的距离．

【答案】（1）证明见解析；（2）455．【分析】（1）连接OB，欲证PO⊥平面ABC，只需证明,POACPOOB⊥⊥即可；（2）方法一：过点C作CHOM⊥，垂足为M，只需论证CH的长即为所求，再利用平面几何知识求解即可.【

详解】（1）因为AP=CP=AC=4，O为AC的中点，所以OP⊥AC，且OP=23．连结OB．因为AB=BC=22AC，222ABBCAC+=，所以△ABC为等腰直角三角形，且OB⊥AC，OB=12AC

=2．由222OPOBPB+=知，OP⊥OB．由OP⊥OB，OP⊥AC，OBACO=，知PO⊥平面ABC．（2）［方法一］：【最优解】定义法作CH⊥OM，垂足为H．又由（1）易知OP⊥平面ABC，从而OP⊥CH，所以CH⊥平面POM．故CH的长为点C到平面POM

的距离．由题设可知OC=12AC=2，CM=23BC=423，∠ACB=45°．所以OM=253，CH=sinOCMCACBOM=455．所以点C到平面POM的距离为455．［方法二］：等积法设C到平面POM的距离为h，由（

1）知PO即为P到平面COM的距离，且POOM⊥．又23PO=，在OMC△中，2422,,4533OCCMBCACB====，则由余弦定理得253OM=，则CPOMPCOMVV−−=，即1133POMCOMShSPO=△△，则22123245

3251252323COMPOMSPOhS===△△．即点C到平面POM的距离为455．［方法三］：向量法如图，以O为原点，建立直角坐标系Oxyz，设(0,0,23)P，(2,0,0)B，(0

,0,0)O，42,,033M，(0,2,0)C，(0,0,23)OP=，42,,033OM=，(0,2,0)OC=．设平面POM的一个法向量(,,)nxyz=，则23=0=042+=0=033zOPnxyOMn，令1x=−，则(1,2

,0)n=−，所以，点C到平面POM的距离为||455||nOCn=．【整体点评】（2）方法一：根据定义法求点到面的距离，是解决点面距问题的首选方法，特别是题目中含有面面垂直的条件，计算简单，是该题的最优解；方法二：根据等积法求点到面的距离，也是解决点面距问

题的常用方法；方法三：当题目中有较好的建系条件，利用向量法解决点面距，思想简单，过程稍繁．37．（2018·全国·高考真题）如图，在平行四边形ABCM中，3ABAC==，90ACM=，以AC为折痕将△ACM折起，使点M

到达点D的位置，且ABDA⊥．（1）证明：平面ACD⊥平面ABC；（2）Q为线段AD上一点，P为线段BC上一点，且23BPDQDA==，求三棱锥QABP−的体积．【答案】(1)证明见解析；(2)1.【分析】(1)根据题意可得BAAC⊥，又BA⊥AD，利用线面垂直的判定定理证得AB

⊥平面ACD，再根据面面垂直的判定定理即可证得；(2)方法一：根据平面知识求出ABPS，再求得三棱锥的高，即可根据三棱锥的体积公式求出.【详解】（1）由已知可得，BAC=90°，BAAC⊥．又BA⊥AD，

且ACADA=，所以AB⊥平面ACD．又AB平面ABC，所以平面ACD⊥平面ABC．（2）［方法一］：定义法由已知可得，DC=CM=AB=3，DA=32．又23BPDQDA==，所以=22BP．作QE⊥AC，垂足为E，则QE=13DC．由已知及（1）可得DC⊥平面ABC，所以QE⊥平面ABC，Q

E=1．因此，三棱锥QABP−的体积为1111322sin451332QABPABPVQES−===．［方法二］：转化法由（1）知，DCAB⊥，又,DCCAABCAA⊥=，所以DC⊥平面ABC，则1932DABCABCVSDC−==△．因为2

1,33DQDAAQDA==，所以1332QABCDABCVV−−==．因为2233BPDABC==，所以213QABPQABCVV−−==．【整体点评】（2）方法一：根据三棱锥的体积公式求底面积和高，是求三

棱锥体积的通性通法；方法二：根据题目的等量关系转化为求易求的三棱锥体积，也是求三棱锥体积的通性通法．38．（2018·全国·高考真题）如图，在三棱锥PABC−中，22ABBC==，4PAPBPCAC====

，O为AC的中点．（1）证明：PO⊥平面ABC；（2）若点M在棱BC上，且二面角MPAC−−为30°，求PC与平面PAM所成角的正弦值．【答案】（1）证明见解析；（2）34.【分析】（1）根据等腰三角形性质得PO垂直AC，再通过计算，根据勾股定理得PO垂直OB，最后根据

线面垂直判定定理得结论；（2）方法一：根据条件建立空间直角坐标系，设各点坐标，根据方程组解出平面PAM一个法向量，利用向量数量积求出两个法向量夹角，根据二面角与法向量夹角相等或互补关系列方程，解得M坐标，再利用向量数量积求得向量PC与平面PAM法向量夹角，最后根据线面角与向量夹角互余得

结果．【详解】（1）因为4APCPAC===，O为AC的中点，所以OPAC⊥，且23OP=．连结OB．因为22ABBCAC==，所以ABC为等腰直角三角形，且1,22OBACOBAC⊥==，由222OPOBPB+=知POOB⊥．由,OPOBOPAC⊥⊥知，PO⊥平面ABC．（2）［方法一］：

【通性通法】向量法如图，以O为坐标原点，OB的方向为x轴正方向，建立空间直角坐标系Oxyz−．由已知得(0,0,0),(2,0,0),(0,2,0),(0,2,0),(0,0,23),(0,2,23)OBACPAP−=取平面PAC的法向

量(2,0,0)OB=．设(,2,0)(02)Maaa−，则(,4,0)AMaa=−．设平面PAM的法向量为(,,)nxyz=．由0,0APnAMn==得2+23=0+(4)=0yzaxay−，可取2(3(4),3,)naaa=−−所以22

223(4)cos23(4)3aOBnaaa−=−++．由已知得3cos2OBn=．所以22223|4|3223(4)3aaaa−=−++．解得4a=−(舍去)，43a=．所以83434,,333n=−−．又(0,2,23)P

C=−，所以3cos,4PCn=．所以PC与平面PAM所成角的正弦值为34．［方法二］：三垂线＋等积法由（1）知PO⊥平面ABC，可得平面PAC⊥平面ABC．如图5，在平面ABC内作MNAC⊥，垂足为N，则MN⊥平面PAC．在平面PAC内作NFAP⊥，垂足为F，联结MF，则

MFAP⊥，故MFN为二面角MPAC−−的平面角，即30MFN=．设MNa=，则,4NCaANa==−，在RtAFN△中，3(4)2FNa=−．在RtMFN△中，由33(4)32aa=−，得43a=，则823FMa==．设点

C到平面PAM的距离为h，由MAPCCAPMVV−−=，得213411844343323h=，解得3h=，则PC与平面PAM所成角的正弦值为34．［方法三］：三垂线＋线面角定义法由（1）知PO

⊥平面ABC，可得平面PAC⊥平面ABC．如图6，在平面ABC内作MNAC⊥，垂足为N，则MN⊥平面PAC．在平面PAC内作NFAP⊥，垂足为F，联结MF，则MFAP⊥，故MFN为二面角MPAC−−的平面角，即30MFN=．同解法1可得43MN

a==．在APC△中，过N作NEPC∥，在FNM△中，过N作NGFM⊥，垂足为G，联结EG．在RtNGM△中，334232233NGNM===．因为NEPC∥，所以843NENAa==−=．由PA⊥平面F

MN，可得平面PAM⊥平面FMN，交线为FM．在平面FMN内，由NGFM⊥，可得NG⊥平面PAM，则NEG为直线NE与平面PAM所成的角．设NEG=，则2333sin843NGNE===，又NEPC∥，所以直线PC与平面PAM所成角的正弦值

为34．［方法四］：【最优解】定义法如图7，取PA的中点H，联结CH，则23CH=．过C作平面PAM的垂线，垂足记为T（垂足T在平面PAM内）．联结HT，则CHT即为二面角MPAC−−的平面角，即30CHT=，得3CT=．联结PT，则CPT为直线PC与平面PAM所成的角．

在RtPCT△中，4,3PCCT==，所以3sin4CPT=．【整体点评】（2）方法一：根据题目条件建系，由二面角的向量公式以及线面角的向量公式硬算即可求出，是该类型题的通性通法；方法二：根据三垂线法找到二面角的平面角，再根据等积

法求出点到面的距离，由定义求出线面角，是几何法解决空间角的基本手段；方法三：根据三垂线法找到二面角的平面角，再利用线面角的等价转化，然后利用定义法找到线面角解出，是几何法解决线面角的基本思想，对于该题，略显麻烦；方法四：直接根据二面角的定义和线面角的定义解决，原理简单，计算简

单，是该题的最优解．39．（2018·全国·高考真题）如图，四边形ABCD为正方形，,EF分别为,ADBC的中点，以DF为折痕把DFC折起，使点C到达点P的位置，且PFBF⊥.（1）证明：平面PEF⊥平面ABFD；（2）求DP与平面ABFD所成角的正弦值.【答案】（1）

证明见解析；（2）34.【分析】（1）依题可知BFPF⊥，BFEF⊥，利用线面垂直的判定定理可得BF⊥平面PEF，再利用面面垂直的判定定理即可证出平面PEF⊥平面ABFD；（2）方法一：依题意建立相应的空间直角坐标系

，求得平面ABFD的法向量，设DP与平面ABFD所成角为，利用线面角的向量公式即可求出．【详解】（1）由已知可得，BFPF⊥，BFEF⊥，又PFEFF=，所以BF⊥平面PEF.又BF平面ABFD，所以平面PEF⊥平面ABFD；（2）[方法一]：向量法作PHEF⊥，垂足为H

.由（1）得，PH⊥平面ABFD.以H为坐标原点，HF的方向为y轴正方向，设1BF=，建立如图所示的空间直角坐标系Hxyz−.由（1）可得，DEPE⊥.又2DP=，1DE=，所以3PE=.又1PF=，2=

EF，故PEPF⊥，可得33,22PHEH==.则()33330,0,0,0,0,,1,,0,1,,,2222DHPDP−−=30,0,2HP=为平面ABFD的法向量.设DP与平面ABFD所成角为，则334sin43HDPDPH

PP===uuuuuruuuruuruur.所以DP与平面ABFD所成角的正弦值为34.[方法2]：向量法如图3所示以E为原点建系．设正方形边长为2，由（1）知，BF⊥平面PEF，则DE⊥平面PEF，故DEPE⊥．易求3PE=，则点P到直线EF的距离为32，从而330,,22P．

又(1,0,0)D−，故331,,22DP=，而平面ABFD的一个法向量(0,0,1)n=，故DP与平面ABFD所成角的正弦值332sin|cos,|24DPnDPnDPn====．[方法3]：【最优解】

定义法如图4，作PHEF⊥，垂足为H，联结DH．由（1）知，PH⊥平面ABFD,因此PDH为DP与平面ABFD所成的角．设正方形ABCD的边长为2，则1DE=，在RtPED△中，3PE=．又因为1,2PFEF==，由222PEPFEF+=知，390,2EPFPH=

=．又因为2PD=，所以在RtPHD△中，3sin4PHPDHPD==．所以DP与平面ABFD所成角的正弦值为34．[方法4]：等积法不妨设=2AB，则1,3,2DEPEDPEF====．PEPF⊥，又,PFPDPDPEP⊥=，所以PF⊥平面PDE．设点P到平面DEF的距离为d

，根据=FPDEPDEFVV−−，即1111131213232d=，解得32d=．于是PD与平面ABFD所成角的正弦值为34dDP=．【整体点评】（2）方法一：建立空间直角坐标系利用线面角的向量公式求解，可算作通

性通法；方法二：同方法一，只是建系方式不一样；方法三：利用线面角的定义求解，计算量小，是该题的最优解；方法四：利用等积法求出点P到平面DEF的距离，再根据线面角的正弦公式即可求出，是线面角的常见求法．40．（2018·天津·高考真题）

如图，在四面体ABCD中，△ABC是等边三角形，平面ABC⊥平面ABD，点M为棱AB的中点，AB=2，AD=23，∠BAD=90°．（Ⅰ）求证：AD⊥BC；（Ⅱ）求异面直线BC与MD所成角的余弦值；（Ⅲ）求直线CD与平面ABD所成角的正弦值．【答案】(Ⅰ

)证明见解析；(Ⅱ)1326；(Ⅲ)34．【详解】分析：（Ⅰ）由面面垂直的性质定理可得AD⊥平面ABC，则AD⊥BC．（Ⅱ）取棱AC的中点N，连接MN，ND．由几何关系可知∠DMN（或其补角）为异面直

线BC与MD所成的角．计算可得113226MNcosDMNDM==．则异面直线BC与MD所成角的余弦值为1326．（Ⅲ）连接CM．由题意可知CM⊥平面ABD．则∠CDM为直线CD与平面ABD所成的角．计算可得34CMsinCDMCD==．即直线CD与平面ABD所成角的正弦值

为34．详解：（Ⅰ）证明：由平面ABC⊥平面ABD，平面ABC∩平面ABD=AB，AD⊥AB，可得AD⊥平面ABC，故AD⊥BC．（Ⅱ）取棱AC的中点N，连接MN，ND．又因为M为棱AB的中点，故MN∥BC．所以∠DMN（或其补角）为异面直线BC与MD所成的角．在Rt△DAM中，

AM=1，故DM=22=13ADAM+．因为AD⊥平面ABC，故AD⊥AC．在Rt△DAN中，AN=1，故DN=22=13ADAN+．在等腰三角形DMN中，MN=1，可得1132cos26MNDMNDM==．所

以，异面直线BC与MD所成角的余弦值为1326．（Ⅲ）连接CM．因为△ABC为等边三角形，M为边AB的中点，故CM⊥AB，CM=3．又因为平面ABC⊥平面ABD，而CM平面ABC，故CM⊥平面ABD．所以，∠CDM为直线CD与平面ABD所成的角．在Rt△CAD中，

CD=22ACAD+=4．在Rt△CMD中，3sin4CMCDMCD==．所以，直线CD与平面ABD所成角的正弦值为34．点睛：本小题主要考查异面直线所成的角、直线与平面所成的角、平面与平面垂直等基础知识．考查空间想象能力、运算求解能力和推理论证能力．41．（2018·全国·高考真题

）如图，几何体是圆柱的一部分，它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的，G是DF的中点.(1)设P是CE上的一点，且AP⊥BE，求∠CBP的大小；(2)当AB＝3，AD＝2时，求二面角E－AG－C的大小.【答案】（1）30；（2）60【

分析】试题分析:(1)第(1)问,直接证明BE⊥平面ABP得到BE⊥BP,从而求出∠CBP的大小.(2)第（2）问，可以利用几何法求，也可以利用向量法求解.【详解】解：(1)因为AP⊥BE，AB⊥BE，AB，AP⊂平面ABP，AB∩AP＝A，所以BE⊥平面ABP.又BP⊂平面ABP，所以BE⊥

BP.又∠EBC＝120°，所以∠CBP＝30°.(2)方法一：如图，取EC的中点H，连接EH，GH，CH.因为∠EBC＝120°，所以四边形BEHC为菱形，所以AE＝GE＝AC＝GC＝223213+=.取AG的中点M，连接EM，CM，EC，则EM⊥AG，CM⊥AG，所以∠EMC为

所求二面角的平面角．又AM＝1，所以EM＝CM＝13123−=.在△BEC中，由于∠EBC＝120°，由余弦定理得EC2＝22＋22－2×2×2×cos120°＝12，所以EC＝23，所以△EMC为等边三角形，故所求的角为

60°.方法二：以B为坐标原点，分别以BE，BP，BA所在的直线为x，y，z轴，建立如图所示的空间直角坐标系B－xyz.由题意得A(0,0,3)，E(2,0,0)，G(1，3，3)，C(－1，3，0)，故AE＝(2,0，－3)，AG＝(1

，3，0)，CG＝(2,0,3)．设m＝(x1，y1，z1)是平面AEG的一个法向量，由00mAEmAG==可得111123030xzxy−=+=取z1＝2，可得平面AEG的一个法向量m＝(3，－3，2)．设n＝(x2，y2，z2)是平面ACG的一个法向量

．由00nAGnCG==可得222230230xyxz+=+=取z2＝－2，可得平面ACG的一个法向量n＝(3，－3，－2)．所以cos〈,mn〉＝||||mnmn＝12.故所求的角为60°.点睛：本题的难点主要是计算，由于空间向量的运算

，所以大家在计算时，务必仔细认真.42．（2017·全国·高考真题）（2017新课标全国Ⅲ理科）如图，四面体ABCD中，△ABC是正三角形，△ACD是直角三角形，∠ABD=∠CBD，AB=BD．（1）证明：

平面ACD⊥平面ABC；（2）过AC的平面交BD于点E，若平面AEC把四面体ABCD分成体积相等的两部分，求二面角D–AE–C的余弦值.【答案】（1）见解析；（2）77.【详解】试题分析：（1）利用题意证得二面角的平面角

为90°，则可得到面面垂直；（2）利用题意求得两个半平面的法向量，然后利用二面角的夹角公式可求得二面角D–AE–C的余弦值为77.试题解析：（1）由题设可得，ABDCBD≌△△，从而ADDC=.又ACD是直角三角形，所以

=90ADC.取AC的中点O，连接DO,BO,则DO⊥AC,DO=AO.又由于ABC是正三角形，故BOAC⊥.所以DOB为二面角DACB−−的平面角.在RtAOB中，222BOAOAB+=.又ABBD=，所以222222BODOBOAOABBD+=+==，故90DOB=.所以平面ACD⊥平

面ABC.（2）由题设及（1）知，,,OAOBOD两两垂直，以O为坐标原点，OA的方向为x轴正方向，OA为单位长，建立如图所示的空间直角坐标系Oxyz−.则()()()()1,0,0,0,3,0,1,

0,0,0,0,1ABCD−.由题设知，四面体ABCE的体积为四面体ABCD的体积的12，从而E到平面ABC的距离为D到平面ABC的距离的12，即E为DB的中点，得310,,22E.故()()311,0,1,2

,0,0,1,,22ADACAE=−=−=−.设(),,nxyz=是平面DAE的法向量，则00nADnAE==，，即0,310.22xzxyz−+=−++=可取31,,

13=n.设m是平面AEC的法向量，则00mACmAE==，，同理可取()0,1,3=−m.则7cos,7==nmnmnm.所以二面角D-AE-C的余弦值为77.【名师点睛】（1）求解本题要注

意两点：一是两平面的法向量的夹角不一定是所求的二面角，二是利用方程思想进行向量运算时，要认真细心，准确计算.（2）设m，n分别为平面α，β的法向量，则二面角θ与,mn互补或相等，故有coscos,mnmnmn==.求解时一定要注意结

合实际图形判断所求角是锐角还是钝角.43．（2017·全国·高考真题）如图，在四棱锥P−ABCD中，AB//CD，且90BAPCDP==.（1）证明：平面PAB⊥平面PAD；（2）若PA=PD=AB=DC，90APD=，求二面角A−PB−C的余弦值.【答案】（1）见解析；（

2）33−.【详解】（1）由已知90BAPCDP==，得AB⊥AP，CD⊥PD．由于AB//CD，故AB⊥PD，从而AB⊥平面PAD．又AB平面PAB，所以平面PAB⊥平面PAD．（2）在平面PAD内作PFAD⊥，垂足为

F，由（1）可知，AB⊥平面PAD，故ABPF⊥，可得PF⊥平面ABCD.以F为坐标原点，FA的方向为x轴正方向，AB为单位长，建立如图所示的空间直角坐标系Fxyz−.由（1）及已知可得2,0,02A

，20,0,2P，2,1,02B，2,1,02C−.所以22,1,22PC=−−，()2,0,0CB=，22,0,22PA=−

，()0,1,0AB=.设(),,nxyz=r是平面PCB的法向量，则0,0,nPCnCB==即220,2220,xyzx−+−==可取()0,1,2n=−−.设(),,mxyz=是平面PAB的法向量，则0,0,mPAmAB==即220,220.x

zy−==可取()1,0,1m=.则3cos,3nmnmnm==−，所以二面角APBC−−的余弦值为33−.【名师点睛】高考对空间向量与立体几何的考查主要体现在以下几个方面：①求异面直线所成的角，关键是转化为两直线的方向向量的夹角；②求直线与平面所成的角，关键是转

化为直线的方向向量和平面的法向量的夹角；③求二面角，关键是转化为两平面的法向量的夹角.建立空间直角坐标系和表示出所需点的坐标是解题的关键.44．（2017·天津·高考真题）如图，在四棱锥PABCD−中，AD⊥平面PDC，A

DBC，PDPB⊥，1AD=，3BC=，4CD=，2PD=.（I）求异面直线AP与BC所成角的余弦值；（II）求证：PD⊥平面PBC；（Ⅲ）求直线AB与平面PBC所成角的正弦值.【答案】（Ⅰ）55.（Ⅱ）见解析;（Ⅲ）55.【分析】（

Ⅰ）由已知AD//BC，故DAP或其补角即为异面直线AP与BC所成的角，然后在Rt△PDA中求解即可；（Ⅱ）因为AD⊥平面PDC，所以AD⊥PD，PD⊥BC，又PD⊥PB，所以PD⊥平面PBC；（Ⅲ）过点

D作AB的平行线交BC于点F，连结PF，则DF与平面PBC所成的角等于AB与平面PBC所成的角，且DFP为直线DF和平面PBC所成的角，然后在Rt△DPF中求解即可.【详解】解：（Ⅰ）如图，由已知AD//BC，故DAP或其补角即为异面直线AP与BC所成的角.因为A

D⊥平面PDC，所以AD⊥PD.在Rt△PDA中，由已知，得225APADPD=+=，故5cos5ADDAPAP==.所以，异面直线AP与BC所成角的余弦值为55.（Ⅱ）证明：因为AD⊥平面PDC，直线PD平面PDC，所以AD⊥PD.又

因为BC//AD，所以PD⊥BC，又PD⊥PB，BCPBB=所以PD⊥平面PBC.（Ⅲ）过点D作AB的平行线交BC于点F，连结PF，则DF与平面PBC所成的角等于AB与平面PBC所成的角.因为PD⊥平面PBC，故PF为DF在平面P

BC上的射影，所以DFP为直线DF和平面PBC所成的角.由于AD//BC，DF//AB，故BF=AD=1，由已知，得CF=BC–BF=2.又AD⊥DC，故BC⊥DC，在Rt△DCF中，可得2225D

FCDCF=+=,在Rt△DPF中，可得5sin5PDDFPDF==.所以，直线AB与平面PBC所成角的正弦值为55.考点：两条异面直线所成的角、直线与平面垂直、直线与平面所成的角【点睛】本小题主要考查两条异面直线所成的角、直线与平面垂直的证明、直线与平面所成的角，要求一定的空间想象能力、运算求

解能力和推理论证能力.求两条异面直线所成的角，首先要借助平行线找出异面直线所成的角，证明线面垂直只需寻求线线垂直，求线面角首先利用转化思想寻求直线与平面所成的角，然后再计算即可.45．（2017·全国·高考真题）如图，四面体

ABCD中，△ABC是正三角形，AD=CD．（1）证明：AC⊥BD；（2）已知△ACD是直角三角形，AB=BD．若E为棱BD上与D不重合的点，且AE⊥EC，求四面体ABCE与四面体ACDE的体积比．【答案】（1）见解析；（2

）1:1.【详解】试题分析：（1）取AC的中点O，由等腰三角形及等边三角形的性质得ACOD⊥，ACOB⊥，再根据线面垂直的判定定理得AC⊥平面OBD，即得AC⊥BD；（2）先由AE⊥EC，结合平面几何知识确定12EOAC=，再根据锥体的体积公式得所求体积之比为1:1.试题解析：（1）取

AC的中点O，连结DO，BO.因为AD=CD，所以AC⊥DO.又由于ABC是正三角形，所以AC⊥BO.从而AC⊥平面DOB，故AC⊥BD.（2）连结EO.由（1）及题设知∠ADC=90°，所以DO=AO.在RtAOB中，222BOAOAB+=.又AB=BD，所以2222

22BODOBOAOABBD+=+==，故∠DOB=90°.由题设知AEC△为直角三角形，所以12EOAC=.又ABC是正三角形，且AB=BD，所以12EOBD=.故E为BD的中点，从而E到平面ABC的距离为D到平面ABC的距离的

12，四面体ABCE的体积为四面体ABCD的体积的12，即四面体ABCE与四面体ACDE的体积之比为1:1.【名师点睛】垂直、平行关系证明中应用转化与化归思想的常见类型：（1）证明线面、面面平行，需转化为证明线线平

行.（2）证明线面垂直，需转化为证明线线垂直.（3）证明线线垂直，需转化为证明线面垂直.46．（2017·全国·高考真题）如图，在四棱锥PABCD−中，ABCD∥，且90BAPCDP==.（1）证明：平面PAB⊥平面PAD；（2）若PAPDABDC===，90APD=，且四棱锥P

ABCD−的体积为83，求该四棱锥的侧面积．【答案】（1）证明见解析；（2）623+.【详解】试题分析：（1）由90BAPCDP==，得ABAP⊥，CDPD⊥．从而得ABPD⊥，进而而AB⊥平面PAD，由面面垂直的判定定理可得平面PAB⊥平面PAD；（2）

设PAPDABDCa====，取AD中点O，连结PO，则PO⊥底面ABCD，且22,2ADaPOa==，由四棱锥PABCD−的体积为83，求出2a=，由此能求出该四棱锥的侧面积.试题解析：（1）由已知90BAP

CDP==，得ABAP⊥，CDPD⊥．由于ABCD∥，故ABPD⊥，从而AB⊥平面PAD．又AB平面PAB，所以平面PAB⊥平面PAD．（2）在平面PAD内作PEAD⊥，垂足为E．由（1）知，AB⊥面PAD，故ABPE⊥，可得PE⊥平面ABCD．

设ABx=，则由已知可得2ADx=，22PEx=．故四棱锥PABCD−的体积31133PABCDVABADPEx−==．由题设得31833x=，故2x=．从而2PAPD==，22ADBC==，22PBPC==．可得四棱锥PABCD−的侧面

积为111222PAPDPAABPDDC++21sin606232BC+=+．47．（2017·北京·高考真题）如图，在三棱锥P－ABC中，PA⊥AB，PA⊥BC，AB⊥BC，PA＝AB＝BC＝2，D为线段AC的中点，E为线段PC上一点.(1)求证：PA⊥BD；(

2)求证：平面BDE⊥平面PAC；(3)当PA∥平面BDE时，求三棱锥E－BCD的体积．【答案】（1）证明见解析；（2）证明见解析；（3）13【详解】试题分析：（Ⅰ）要证明线线垂直，一般转化为证明线面垂直；（Ⅱ）要证明面面垂直，一般转化为证明线面垂直、线线垂直；（Ⅲ）由13BCDVSDE

=即可求解.试题解析:（I）因为PAAB⊥，PABC⊥，所以PA⊥平面ABC，又因为BD平面ABC，所以PABD⊥.（II）因为ABBC=，D为AC中点，所以BDAC⊥，由（I）知，PABD⊥，所以

BD⊥平面PAC.所以平面BDE⊥平面PAC.（III）因为PA平面BDE，平面PAC平面BDEDE=，所以PADE.因为D为AC的中点，所以112DEPA==，2BDDC==.由（I）知，PA⊥平面ABC，所以DE⊥平面PAC.所以三棱锥EBCD−的

体积1163VBDDCDE==.【名师点睛】线线、线面的位置关系以及证明是高考的重点内容，而其中证明线面垂直又是重点和热点，要证明线面垂直，根据判定定理可转化为证明线与平面内的两条相交直线垂直，也可根据性质定理转化为证明面面垂直.48．（2017·江苏·高考真题）如图，在三棱

锥A­BCD中，AB⊥AD，BC⊥BD，平面ABD⊥平面BCD，点E，F(E与A，D不重合)分别在棱AD，BD上，且EF⊥AD.求证：(1)EF∥平面ABC；(2)AD⊥AC.【答案】（1）见解析（2）见解析【详解】试题分析：（1）先由平面几

何知识证明EFAB∥，再由线面平行判定定理得结论；（2）先由面面垂直性质定理得BC⊥平面ABD，则BC⊥AD，再由AB⊥AD及线面垂直判定定理得AD⊥平面ABC，即可得AD⊥AC．试题解析：证明：（1）在平面ABD内，因为AB⊥AD，EFAD⊥

，所以EFAB.又因为EF平面ABC，AB平面ABC，所以EF∥平面ABC.（2）因为平面ABD⊥平面BCD，平面ABD平面BCD=BD，BC平面BCD，BCBD⊥，所以BC⊥平面ABD.因为AD平面ABD，所以BC⊥AD.又AB⊥AD，BCABB=，AB

平面ABC，BC平面ABC，所以AD⊥平面ABC，又因为AC平面ABC，所以AD⊥AC.点睛:垂直、平行关系证明中应用转化与化归思想的常见类型：（1）证明线面、面面平行，需转化为证明线线平行；（2）证明线面垂直，需转化为证明线线垂直；（3）证明线线垂直

，需转化为证明线面垂直．49．（2016·浙江·高考真题）如图，在三棱台ABC–DEF中，平面BCFE⊥平面ABC，∠ACB=90°，BE=EF=FC=1，BC=2，AC=3.（Ⅰ）求证：BF⊥平面ACFD；（Ⅱ）求直线BD与平面ACFD所成角的余弦

值.【答案】（1）证明详见解析；（2）217.【详解】试题分析：本题主要考查空间点、线、面位置关系，线面角等基础知识，同时考查空间想象能力和运算求解能力．试题解析：（Ⅰ）延长,,ADBECF相交于一点K，如图所示.因为平面BCFE⊥平面ABC，且ACBC⊥，所以AC⊥平面BCK，因此，B

FAC⊥.又因为//EFBC，1BEEFFC===，2BC=，所以BCK为等边三角形，且F为CK的中点，则BFCK⊥所以BF⊥平面ACFD.（Ⅱ）因为BF⊥平面ACK，所以BDF是直线BD与平面ACFD所成的角.在RtBFD中，33,2BFDF==，得21cos7BD

F=.所以，直线BD与平面ACFD所成的角的余弦值为217.【考点】空间点、线、面位置关系、线面角.【方法点睛】解题时一定要注意直线与平面所成的角的范围，否则很容易出现错误．证明线面垂直的关键是证明线线垂直，证明线线垂直常用的方法是直角三角形、等腰三角形的“三线合一”和菱形、正方形的对角

线．50．（2016·北京·高考真题）如图，在四棱锥中，平面，,ABDCDCAC⊥∥.（Ⅰ）求证：DCPAC⊥平面；（Ⅱ）求证：PABPAC⊥平面平面；（Ⅲ）设点E为AB的中点，在棱PB上是否存在点F，使得//平面CΕF?说明理由.【答案】（Ⅰ）见解

析；（Ⅱ）见解析；（Ⅲ）存在.理由见解析.【分析】（Ⅰ）利用线面垂直判定定理证明；（Ⅱ）利用面面垂直判定定理证明；（Ⅲ）取PB中点F，连结EF，则F//，根据线面平行的判定定理证明//平面CΕF.【详

解】（Ⅰ）因为平面，所以CDC⊥．又因为DCC⊥，所以DC⊥平面ΡΑC．（Ⅱ）因为//DC，DCC⊥，所以C⊥．因为平面，所以C⊥．所以⊥平面ΡΑC．所以平面ΡΑΒ⊥平面ΡΑC．（Ⅲ）棱PB上存在点F，使得//平面CΕF．证明如下：取PB中点F，连结EF，C

，CF．又因为E为的中点，所以F//．又因为ΡΑ平面CΕF，所以//平面CΕF．51．（2016·全国·高考真题）如图，菱形ABCD的对角线AC与BD交于点O，点,EF分别在,ADCD上，,AECFEF=交BD于点H，将DEF沿EF折起到DEF的位置.（

Ⅰ）证明：ACHD⊥；（Ⅱ)若55,6,,224ABACAEOD====，求五棱锥DABCFE−的体积.【答案】（Ⅰ）详见解析；（Ⅱ）2322.【详解】试题分析：（1）由已知得，,ACBDADCD⊥=，AECF=AECFADCD=//ACEF,⊥⊥EF

HDEFHDACHD⊥；（2）由//EFAC14OHAEDOAD==，由5,6ABAC==224DOBOABAO==−=1,3OHDHDH===()22222219ODOHDH+=+==ODOH⊥，可证OD⊥平面ABC．又由EFDH

ACDO=得92EF=五边形ABCFE的面积1682S=19693224−=以五棱锥DABCEF−体积16923222342V==．试题解析：（1）由已知得，,ACBDADCD⊥=，又由AECF=得AECFADCD=，故//ACEF，由

此得,⊥⊥EFHDEFHD，所以ACHD⊥．（2）由//EFAC得14OHAEDOAD==，由5,6ABAC==得224DOBOABAO==−=，所以1,3OHDHDH===，于是()22222219ODOHDH+=+==，故ODOH⊥，由（1）知ACHD⊥

，又,⊥=ACBDBDHDH，所以AC⊥平面BHD，于是ACOD⊥，又由,⊥=ODOHACOHO，所以，OD⊥平面ABC．又由EFDHACDO=得92EF=．五边形ABCFE的面积119696832224S=

−=．所以五棱锥DABCEF−体积16923222342V==．考点：1、线线垂直；2、锥体的体积.52．（2016·北京·高考真题）如图，在四棱锥PABCD−中，平面PAD⊥平面ABCD，PAPD⊥，PAPD

=，ABAD⊥，1AB=，2AD=，5ACCD==.（1）求证：平面PAB；（2）求直线PA与平面PCD所成角的正弦值；（3）在棱上是否存在点，使得平面PCD？若存在，求的值；若不存在，说明理由.【答案】（1）见解析；（2）33；（3）存在，14AMAP=【详解】试题

分析：（1）由面面垂直性质定理知AB⊥平面；根据线面垂直性质定理可知，再由线面垂直判定定理可知平面；（2）取的中点，连结PO，CO，以为坐标原点建立空间直角坐标系Oxyz−，利用向量法可求出直线PB与平面PCD所成角的正弦值；（3）假设存在，根据A，P，M三点共线，设，根据//BM

平面PCD，即，求的值，即可求出AMAP的值.试题解析：（1）因为平面PAD⊥平面ABCD，ABAD⊥，所以平面，所以，又因为，所以平面；（2）取的中点，连结PO，CO，因为PAPD=，所以.又因为平面，

平面PAD⊥平面，所以平面.因为平面，所以CO.因为，所以.如图建立空间直角坐标系，由题意得，.设平面的法向量为，则即令，则.所以.又，所以.所以直线PB与平面所成角的正弦值为.（3）设是棱上一点，则存在使得.因此点.因为平面，所以BM∥平面当且仅当，即，解得.所以在棱上存

在点使得平面，此时.考点：1.空间垂直判定与性质；2.异面直线所成角的计算；3.空间向量的运用.53．（2016·山东·高考真题）在如图所示的几何体中，D是AC的中点，EF∥DB．（Ⅰ）已知AB=BC，AE=EC．求证：AC⊥FB；（Ⅱ）已知G,H分别是EC和FB的中点.求证：

GH∥平面ABC．【答案】（Ⅰ）证明：见解析；（Ⅱ）见解析.【详解】试题分析：（Ⅰ）根据，知与确定一个平面，连接，得到，，从而平面，证得.（Ⅱ）设的中点为，连，在CEF△，CFB中，由三角形中位线定理可得线线平行，证得平面

平面，进一步得到平面.试题解析：（Ⅰ）证明：因，所以与确定平面.连接，因为,AEECD=为的中点，所以，同理可得.又，所以平面，因为平面，所以.（Ⅱ）设的中点为，连.在CEF△中，因为是的中点，所以，又，所以.在CFB中，因为是的中点，所以，又，所以平面平面，因为平面，所以平面.【考点】平行

关系，垂直关系【名师点睛】本题主要考查直线与直线垂直、直线与平面平行.此类题目是立体几何中的基本问题.解答本题，关键在于能利用已知的直线与直线、直线与平面、平面与平面的位置关系，通过严密推理，给出规范的证明.本题能较好地考查考生的空间想象能力、逻辑推理能力及转化与

化归思想等.54．（2016·浙江·高考真题）如图,在三棱台ABCDEF−中,平面BCFE⊥平面ABC,90,2ACBBC==，3,1ACBEEFFC====.（Ⅰ）求证：BF⊥平面ACFD；（Ⅱ）求二面角BADF−−的平面角

的余弦值.【答案】（Ⅰ）见解析；（Ⅱ）34．【分析】（Ⅰ）延长AD，BE，CF相交于一点K，先证BFAC⊥，再证BFCK⊥，进而可证F⊥平面ACFD；（Ⅱ）方法一：先找二面角BADF−−的平面角，再在RtBQF△中计算，即

可得二面角BADF−−的平面角的余弦值；方法二：先建立空间直角坐标系，再计算平面ACK和平面ABK的法向量，进而可得二面角BADF−−的平面角的余弦值．【详解】（Ⅰ）延长AD，BE，CF相交于一点K，如图所示．因为平面BCFE

⊥平面ABC，平面BCFE平面ABCBC=，且ACBC⊥，所以AC⊥平面BCK，BF平面BCK，因此BFAC⊥．又因为//EFBC，1BEEFFC===，2BC=，所以BCK为等边三角形，且F为CK的中点，则,BFCKCKACC⊥=．所以BF⊥平面ACF

D．（Ⅱ）方法一：过点F作FQAK⊥于Q，连结BQ．因为BF⊥平面ACK，所以BFAK⊥，BFFQF=，则⊥AK平面BQF，所以BQAK⊥．所以BQF是二面角BADF−−的平面角．在RtACK中，3AC=，2CK=，得31313FQ=．在RtBQF△中，3

1313FQ=，3BF=，得3cos4BQF=．所以二面角BADF−−的平面角的余弦值为34．方法二：如图，延长,,ADBECF相交于一点K，则BCK为等边三角形．取BC的中点O，则KOBC⊥，又平面BCFE⊥平面ABC，所以，KO⊥平面ABC．以点O为原点，分别以射线OB

，OK的方向为x，z的正方向，建立空间直角坐标系Oxyz．由题意得()1,0,0B，()1,0,0C−，(0,0,3)K，()1,3,0A−−，13(,0,)22E，13(,0,)22F−．因此，()0,3,0AC=，()1,3

,3AK=，()2,3,0AB=．设平面ACK的法向量为111(,,)mxyz=，平面ABK的法向量为222(,,)nxyz=．由00ACmAKm==，得111130330yxyz=++=，取()3,0,1m=−；由00ABnAKn==，得22

222230330xyxyz+=++=取()3,2,3n=−．于是，3333cos,431943mnmnmn−===+++．所以，二面角BADF−−的平面角的余弦值为34．【点睛】解题时

一定要注意二面角的平面角是锐角还是钝角，否则很容易出现错误．证明线面垂直的关键是证明线线垂直，证明线线垂直常用的方法是直角三角形、等腰三角形的“三线合一”和菱形、正方形的对角线．55．（2016·天津·高考真题）如图，四边形ABCD是平行四边形，平面AED⊥平面ABCD，EF||AB，AB

=2，BC=EF=1，AE=6，DE=3，∠BAD=60º，G为BC的中点.（Ⅰ）求证：FG||平面BED；（Ⅱ）求证：平面BED⊥平面AED；（Ⅲ）求直线EF与平面BED所成角的正弦值.【答案】（Ⅰ）详见解析（Ⅱ）详见解析（Ⅲ）【详解】试题分析：（

Ⅰ）证明线面平行，一般利用线面平行判定定理，即从线线平行出发给予证明，而线线平行寻找与论证，往往结合平面几何知识，如本题构造一个平行四边形：取的中点为，可证四边形是平行四边形，从而得出（Ⅱ）面面垂直的证明，一般转化为证线面垂直，而线面垂直的证明，往往需

多次利用线面垂直判定与性质定理，而线线垂直的证明有时需要利用平面几何的知识，如本题可由余弦定理解出，即（Ⅲ）求线面角，关键作出射影，即面的垂线，可利用面面垂直的性质定理得到线面垂直，即面的垂线：过点作于点，则平

面，从而直线与平面所成角即为.再结合三角形可求得正弦值试题解析：（Ⅰ）证明：取的中点为，连接，在中，因为是的中点，所以且，又因为，所以且，即四边形是平行四边形，所以，又平面，平面，所以平面.（Ⅱ）证明：在中，，由余弦定理可，进而可得，即，又因为平面平面平面；平面平面，所以平面.又因为平面，所以平面

平面.（Ⅲ）解：因为，所以直线与平面所成角即为直线与平面所成角.过点作于点，连接，又因为平面平面，由（Ⅱ）知平面，所以直线与平面所成角即为.在中，，由余弦定理可得，所以，因此，在中，，所以直线与平面所成角的正弦值为考点：直线与平面平行和垂直、平面与平面垂直、直线与平面

所成角56．（2016·全国·高考真题）如图，菱形ABCD的对角线AC与BD交于点,5,6OABAC==，点,EF分别在,ADCD上，5,4AECFEF==交BD于点H，将DEF沿EF折到DEF位置，10OD=.（1）证明：DH⊥平面AB

CD；（2）求二面角BDAC−−的正弦值.【答案】（1）证明见解析；（2）29525.【详解】试题分析：(1)证明线面垂直，一般利用线面垂直判定定理，即利用线线垂直进行论证，而线线垂直的寻找与论证往往需要利用

平面几何条件，如本题需利用勾股定理经计算得出线垂直（2）一般可利用空间向量的数量积求二面角的大小，首先根据题意建立恰当的直角坐标系，设立各点坐标，利用方程组解出各面的法向量，再根据向量数量积求出两个法向量的夹角的余

弦值，最后根据二面角与法向量夹角关系确定二面角的余弦值.试题解析：(1)由已知得ACBD⊥，ADCD=,又由AECF=得AECFADCD=，故AC∥EF，因此EFHD⊥，从而EF⊥DH.由56ABAC==，得224DO

BOABAO==−=.由AC∥EF得14OHAEDOAD==.所以1OH=,3DHDH==.于是222223110DHOHDO+=+==,故DHOH⊥.又DHEF⊥,而OHEFH=,所以DH⊥平面ABCD.如图，以H为坐标原点，HF的方向为x轴的正方向，建立空间直角坐

标系Hxyz−，则()0,0,0H，()3,1,0A−−，()0,6,0B−，()3,1,0C−，()0,0,3D，()3,4,0AB=−，()6,0,0AC=，()3,1,3AD=.设()111,,mxyz=r是平面ABD的法向量，则0{0mA

BmAD==，即11111340{330xyxyz−=++=，可取()4,3,5m=−.设()222,,nxyz=r是平面ACD的法向量，则0{0nACnAD==，即222260{330xxyz=++=，可取()0,3,1n=−于是1475cos,255010mnm

nmn−===−，设二面角的大小为，295sin25=.因此二面角BDAC−−的正弦值是29525.点睛：利用法向量求解空间线面角的关键在于“四破”：第一，破“建系关”，构建恰当的空间直角坐标系；第二，破“求坐标关”，准确求解相关点的坐标；第三，破“求法向量关”，求出平面的法向量；第四，

破“应用公式关”.57．（2016·全国·高考真题）如图，在以A，B，C，D，E，F为顶点的五面体中，四边形ABEF为正方形，2AFFD=，90AFD=，且二面角DAFE−−与二面角CBEF−−都是60.（1）证明：平面ABEF⊥平面EFDC；（2）求二面角EBCA

−−的余弦值.【答案】（1）见解析；（2）21919−.【分析】（Ⅰ）证明AF⊥平面EFDC，结合AF平面ABEF，可得平面ABEF⊥平面EFDC．（Ⅱ）建立如图所示的空间坐标系，求出平面EBC的法向量和平面BCA的法向量的夹角的余弦值后可得所求的二面角的余弦值.【详解】（Ⅰ）因为四边形ABEF

为正方形，所以AFFE⊥，又AFDF⊥，DFFEF=，所以AF⊥平面EFDC．又AF平面ABEF，故平面ABEF⊥平面EFDC．（Ⅱ）过D作DGEF⊥，垂足为G，因为平面ABEF⊥平面EFDC，平面ABEF

平面EFDCEF=，DG平面EFDC，故DG⊥平面ABEF．以G为坐标原点，GF的方向为x轴正方向，GD的方向为z轴正向，建立如图所示的空间直角坐标系Gxyz−．由（Ⅰ）知DFE为二面角DAFE−−的平面角，故60DFE=，设()20DFaa

=，则3DGa=，FGa=，所以(),4,0Aaa，()3,4,0Baa−，()3,0,0Ea−，()0,0,3Da．由已知，//ABEF，而AB平面EFDC，EF平面EFDC，所以//AB平面EFDC，又平面ABCD平面EFDC

DC=，AB平面ABCD，故//ABCD，所以//CDEF．由//BEAF，可得BE⊥平面EFDC，同理CEF为二面角CBEF−−的平面角，所以60CEF=，从而可得()2,0,3Caa−．所以(),0,3ECaa=，()0,4,0EBa=，()3,4,

3ACaaa=−−，()4,0,0ABa=−．设(),,nxyz=是平面BCE的法向量，则00nECnEB==，即3040axazay+==，取3x=，则0,3yz==−，可取()3,0,3n=−．设m是平面

ABCD的法向量，则00mACmAB==，同理可取()0,3,4m=，则43219cos,192319nmnmnm==−=−．因为二面角EBCA−−的平面角为钝角，故二面角EBCA−−的余弦值为21919−．【点睛】立体几何解答题第一问通常考查线面位

置关系的证明,空间中线面位置关系的证明主要包括线线、线面、面面三者的平行与垂直关系,其中推理论证的关键是结合空间想象能力进行推理,注意防止步骤不完整或考虑不全致推理片面,该类题目难度不大,以中档题为主.第二问一般考

查角度问题,多用空间向量法解决.58．（2015·广东·高考真题）如图，三角形△PDC所在的平面与长方形ABCD所在的平面垂直，PD＝PC＝4，AB＝6，BC＝3，点E是CD的中点，点F、G分别在线段AB、BC上，且AF＝2FB，CG＝

2GB．（1）证明：PE⊥FG；（2）求二面角P﹣AD﹣C的正切值；（3）求直线PA与直线FG所成角的余弦值．【答案】（1）见解析；（2）73；（3）9525．【分析】（1）通过△PDC为等腰三角形可得PE⊥CD，利用线面垂直判定定理及性质定理即得结论；（2）通过（1）及面面垂直定理可

得PG⊥AD，则∠PDC为二面角P﹣AD﹣C的平面角，利用勾股定理即得结论；（3）连结AC，利用勾股定理及已知条件可得FG∥AC，在△PAC中，利用余弦定理即得直线PA与直线FG所成角的余弦值．【详解】（1）证明：在△PDC中PO＝PC且E为CD中

点，∴PE⊥CD，又∵平面PDC⊥平面ABCD，平面PDC∩平面ABCD＝CD，PE⊂平面PCD，∴PE⊥平面ABCD，又∵FG⊂平面ABCD，∴PE⊥FG；（2）解：由（1）知PE⊥平面ABCD，∴PE⊥AD，又∵CD⊥AD且PE∩CD＝

E，∴AD⊥平面PDC，又∵PD⊂平面PDC，∴AD⊥PD，又∵AD⊥CD，∴∠PDC为二面角P﹣AD﹣C的平面角，在Rt△PDE中，由勾股定理可得：PE2222437PDDE=−=−=，∴tan∠PD

C73PGDG==；（3）解：连结AC，则AC2263=+=35，在Rt△ADP中，AP222234ADDP=+=+=5，∵AF＝2FB，CG＝2GB，∴FG∥AC，∴直线PA与直线FG所成角即为直线PA与直线AC所成

角∠PAC，在△PAC中，由余弦定理得cos∠PAC2222PAACPCPAAC+−=2225(35)42535+−=9525=．【点睛】本题考查线线垂直的判定、二面角及线线角的三角函数值，涉及到勾股定理、余弦定理等知识，注意解题方法的积累，属于中档

题．59．（2015·江苏·高考真题）如图，在直三棱柱中，已知，，设的中点为，.求证：（1）；（2）.【答案】（1）详见解析（2）详见解析【详解】试题分析（1）由三棱锥性质知侧面11BBCC为平行四边形,因此点E为1BC的中点，从而由三角形中位线性质得//DEAC，再由线面平行判定定理得（2）因

为直三棱柱中，所以侧面11BBCC为正方形，因此11BCBC⊥，又，1ACCC⊥（可由直三棱柱推导），因此由线面垂直判定定理得11ACBBCC⊥平面,从而1ACBC⊥，再由线面垂直判定定理得11BCABC⊥平面,进而可得试题解析：（1）由题意知，为1C的中点，又D为1的中点

，因此D//C．又因为D平面11CC，C平面11CC，所以D//平面11CC．（2）因为棱柱111CC−是直三棱柱，所以1CC⊥平面C．因为C平面C，所以1CCC

⊥．又因为CC⊥，1CC平面11CC，C平面11CC，1CCCC=，所以C⊥平面11CC．又因为1C平面11CC，所以1CC⊥．因为1CCC=，所以矩形11CC是正方形，因此11CC⊥．因为C，1C平面1C，1

CCC=，所以1C⊥平面1C．又因为1平面1C，所以11C⊥．考点：线面平行判定定理，线面垂直判定定理60．（2015·重庆·高考真题）如图，三棱锥P-ABC中，平面PAC⊥平面ABC，ABC=2，点D、E在线段

AC上，且AD=DE=EC=2，PD=PC=4，点F在线段AB上，且EF//BC．(Ⅰ)证明：AB⊥平面PFE.(Ⅱ)若四棱锥P-DFBC的体积为7，求线段BC的长.【答案】(1)见解析(2)BC=3或BC=33【分析】（Ⅰ）先由已知易得PEAC⊥，再注意平面PAC

⊥平面ABC，且交线为AC，由面面垂直的性质可得PE⊥平面ABC，再由线面垂直的性质可得到ABPE⊥，再注意到//EFBC，而BCAB⊥，从而有ABEF⊥，那么由线面垂的判定定理可得AB⊥平面PFE，（Ⅱ）设BC=x则可用x将四棱锥PDFBC−的体积表示出来，由已知其体积等于

7，从而得到关于x的一个一元方程，解此方程，再注意到0x即可得到BC的长．【详解】证明：如题（20）图.由,DEECPDPC==知，E为等腰PDC中DC边的中点，故PEAC⊥，又平面PAC⊥平面ABC，平面P

AC平面ABCAC=，PE平面PAC，PEAC⊥，所以PE⊥平面ABC，从而PEAB⊥.因ABC=,,ABEF2EFBC⊥故.从而AB与平面PFE内两条相交直线PE，EF都垂直，所以AB⊥平面PFE.（2）解：设BC=x,则在

直角ABC中，222AB=AC=36BCx−−.从而211SABBC=3622ABCxx=−由EFBC∥，知23AFAEABAC==，得AEFABC,故224()S39AEFABCS==，即4S9AEFABCS=.由1AD=2AE,211421SS=SS36

22999AFBAFEABCABCxx===−,从而四边形DFBC的面积为22DFBC11SS-=363629ABCADFSxxxx=−−−273618xx=−由（1）知，PEPE⊥平面ABC，所以PE为四棱锥P-DFBC

的高.在直角PEC中，2222PE=PC4223EC−=−=,体积2DFBC117S362373318PDFBCVPExx−==−=,故得42362430xx−+=，解得29x=或227x=由于0x，可得333xx==或.所以3BC=或

33BC=.考点：1.空间线面垂直关系，2.锥体的体积，3.方程思想.61．（2015·重庆·高考真题）如图，三棱锥−PABC中，PC⊥平面ABC，3PC=，2ACB=．,DE分别为线段,ABBC上的点，且2

,22CDDECEEB====．(1)证明：DE⊥平面PCD；(2)求二面角APDC−−的余弦值．【答案】（1）见解析；（2）36【详解】试题分析：（1）要证线面垂直，就是要证线线垂直，题中由PC⊥平面ABC，可知PCDE⊥，再分析已知由2,2DCDECE===

得CDDE⊥，这样与DE垂直的两条直线都已找到，从而可得线面垂直；（2）求二面角的大小，可心根据定义作出二面角的平面角，求出这个平面角的大小，本题中，由于2ACB=，PC⊥平面ABC，因此,,CACBCP两两垂直，可以

他们为,,xyz轴建立空间直角坐标系，写出图中各点的坐标，求出平面APD和平面CPD的法向量12,nn，向量12,nn的夹角与二面角相等或互补，由此可得结论．试题解析：（1）证明：由PC⊥平面ABC，DE平面ＡＢＣ，故PC⊥DE由CE＝２，CD

=DE＝２得ＣＤＥ为等腰直角三角形，故CD⊥DE由PCCD=C，DE垂直于平面PCD内两条相交直线，故DE⊥平面PCD（2）解：由（１）知，CDE为等腰直角三角形，DCE＝4,，如（１９）图，过点Ｄ作DF垂直CE于Ｆ，易知DF＝FC＝EF＝１，又已知E

B＝１，故FB＝２．由ACB＝2,得DF//AC，23DFFBACBC==，故AC＝32DF＝32．以Ｃ为坐标原点，分别以,CACBCP，的方程为x轴，y轴，z轴的正方向建立空间直角坐标系，则Ｃ（0,0,0,），Ｐ（0,0,3），Ａ（32,0,0）,Ｅ（0,2,0），Ｄ（1

,1,0），(1,1,0),ED=−(1,1,3)(,1,0)DPDA１，２=−−=−设平面PAD的法向量111,,)nxyz１＝（，由0nDP=１，0nDA=１，得11111130{(2,1,10+)12xyznxy故可取−−==−=.由（1）可知DE⊥平面PCD，故平面PCD的

法向量2nuur可取为ED,即2(1,1,0)n=−.从而法向量1nur，2nuur的夹角的余弦值为1212123,=6||||nncosnnnn=，故所求二面角A-PD-C的余弦值为36.考点：考查线面垂直，二面角．考查空间想象能力和推理能力．62．（2015·浙江·高考真题）如图，

在三棱锥111ABCABC−中，11BAC90ABAC2,4,AAA====，在底面ABC的射影为BC的中点，D为11BC的中点.（1）证明：11DABCA⊥平面；（2）求直线1AB和平面11BCBC所成的角的正弦值.【答案】（1）见解析；（2）78【详解】（1）利用线面垂直的定义得到线线垂直，

根据线面垂直的判定证明直线与平面垂直；（2）通过添加辅助线，证明1AF⊥平面11BBCC，以此找到直线与平面所成角的平面角1ABF，在直角三角形1ABF中通过确定边长，计算1ABF的正弦值.试题解析：（1）设为C中点，由题意得1AE⊥平面C，所以1AEAE⊥.因为ABAC=，所

以AEBC⊥.所以⊥AE平面1ABC.由D，分别为11,BCBC的中点，得1//DEBB且1DEBB=，从而1//DEAA且1DEAA=，所以1AADE是平行四边形，所以1//ADAE.因为⊥AE平面1ABC，所以1AD⊥平面1ABC.（2）作1AFDE⊥，垂足为F，连结F.

因为⊥AE平面1ABC，所以1BCAE⊥.因为BCAE⊥，所以BC⊥平面1AADE.所以11,BCAFAF⊥⊥平面11BBCC.所以1ABF为直线1AB与平面11BBCC所成角的平面角.由2,90A

BACCAB===，得2EAEB==.由⊥AE平面1ABC，得1114,14AAABAE===.由1114,2,90DEBBDAEADAE=====，得172AF=.所以17sin8ABF=考点：1.空间直线、平面垂直关系的证明；2.直线与平面所成的角.63．（2015

·浙江·高考真题）如图，在三棱柱111ABCABC--中，90BAC=，2ABAC==，14AA=，1A在底面ABC的射影为BC的中点，D为11BC的中点.（1）证明：1AD⊥平面1ABC；（2）求二面角1A-BD-1B的平面角的余弦值.【答案】（1）详见解析；（2）18−.【详解】（1）根据条

件首先证得⊥AE平面1ABC，再证明1//ADAE，即可得证；（2）作1AFBD⊥，且，可证明11AFB为二面角11ABDB−−的平面角，再由余弦定理即可求得111cos8AFB=−，从而求解.试题解析：（1）设E为BC的中点，由题意得1AE⊥平面ABC，∴1AEA

E⊥，∵ABAC=，∴AEBC⊥，故⊥AE平面1ABC，由D，E分别11BC，BC的中点，得1//DEBB且1DEBB=，从而1//DEAA，∴四边形1AAED为平行四边形，故1//ADAE，又∵⊥AE平面11ABC，∴1AD

⊥平面11ABC；（2）作1AFBD⊥，且，连结1BF，由2AEEB==，1190AEAAEB==，得114ABAA==，由11ADBD=，11ABBB=，得11ADBBDB，由1AFBD⊥，得1BFBD⊥，因此11AFB为二面角11ABDB−−的平面角，由

12AD=，14AB=，190DAB=，得32BD=，1143AFBF==，由余弦定理得，111cos8AFB=−.考点：1.线面垂直的判定与性质；2.二面角的求解64．（2015·全国·高考真题）如图四边形ABCD为菱形，G为AC与BD交点，BEABCD⊥平面，（I）证明：平面AEC⊥平面

BED；（II）若120ABC=，,AEEC⊥三棱锥EACD−的体积为63，求该三棱锥的侧面积.【答案】（1）见解析（2）3+25【分析】（1）由四边形ABCD为菱形知AC⊥BD，由BE⊥平面ABCD知AC⊥BE，由线面垂直判定定理知AC⊥平面BED，

由面面垂直的判定定理知平面AEC⊥平面BED；（2）设AB=x，通过解直角三角形将AG、GC、GB、GD用x表示出来，在RtAEC中，用x表示EG，在RtEBG中，用x表示EB，根据条件三棱锥EACD−的体积为63求出x，即可求出三棱锥EACD

−的侧面积.【详解】（1）因为四边形ABCD为菱形，所以AC⊥BD，因为BE⊥平面ABCD，所以AC⊥BE，故AC⊥平面BED.又AC平面AEC，所以平面AEC⊥平面BED（2）设AB=x，在菱形ABCD中，由ABC=120°，可得AG=GC=32x,GB=GD=

2x.因为AE⊥EC，所以在RtAEC中，可得EG=32x.连接EG，由BE⊥平面ABCD，知EBG为直角三角形，可得BE=22x.由已知得，三棱锥E-ACD的体积3116632243EACDVACGDBEx−===.故x=2从而可得AE=E

C=ED=6.所以EAC的面积为3，EAD的面积与ECD的面积均为5.故三棱锥E-ACD的侧面积为3+25.【点睛】本题考查线面垂直的判定与性质；面面垂直的判定；三棱锥的体积与表面积的计算；逻辑推理能力；运算求解能力.65．（2015·全国·高考真题）（2015新课标全

国Ⅰ理科）如图，四边形ABCD为菱形，∠ABC=120°，E，F是平面ABCD同一侧的两点，BE⊥平面ABCD，DF⊥平面ABCD，BE=2DF，AE⊥EC．（1）证明：平面AEC⊥平面AFC；（2）求直线AE与直线CF所成角的余弦值

．【答案】（1）见解析；（2）33.【详解】试题分析：（Ⅰ）连接BD，设BD∩AC=G，连接EG，FG，EF，在菱形ABCD中，不妨设GB=1易证EG⊥AC，通过计算可证EG⊥FG，根据线面垂直判定定理可知EG⊥平面AFC，由面面垂直判定定理知平面AFC⊥平面AEC；（Ⅱ）以G为坐标原点，分别以

,GBGC的方向为x轴，y轴正方向，||GB为单位长度，建立空间直角坐标系G-xyz，利用向量法可求出异面直线AE与CF所成角的余弦值.试题解析：（Ⅰ）连接BD，设BD∩AC=G，连接EG，FG，EF，在菱形ABCD中，不妨设GB=1，由∠ABC=120°，可得AG=GC=3.由BE⊥平面ABC

D，AB=BC可知，AE=EC，又∵AE⊥EC，∴EG=3，EG⊥AC，在Rt△EBG中，可得BE=2，故DF=22.在Rt△FDG中，可得FG=62.在直角梯形BDFE中，由BD=2，BE=2，DF=22可得EF=322，∴222EGFGEF+=，∴EG⊥FG，∵AC∩FG=G，∴EG⊥

平面AFC，∵EG面AEC，∴平面AFC⊥平面AEC.（Ⅱ）如图，以G为坐标原点，分别以,GBGC的方向为x轴，y轴正方向，||GB为单位长度，建立空间直角坐标系G-xyz，由（Ⅰ）可得A（0，－3，0），E（1,0,2），F（－1,0，22），C（0，3，0），∴A

E=（1，3，2），CF=（-1，-3，22）.…10分故3cos,3AECFAECFAECF==−.所以直线AE与CF所成的角的余弦值为33.考点：空间垂直判定与性质；异面直线所成角的计算；空间想象能力，推理论证能力66．（2015

·天津·高考真题）如图,已知1AA⊥平面ABC,AB=AC=3,,,点E,F分别是BC,11AB的中点.（Ⅰ）求证:EF∥平面;（Ⅱ）求证:平面平面1BCB.（Ⅲ）求直线与平面1BCB所成角的大小.【答案】（Ⅰ）见试题解析;（Ⅱ）见试题解析;（Ⅲ）30.【详解】（Ⅰ

）要证明EF∥平面11ABBA,只需证明11ABN且EF平面11ABBA;（Ⅱ）要证明平面11ABN平面1BCB,可证明AEBC⊥,1BBAE^;（Ⅲ）取1AN中点N,连接11AB,则1AEA^就是直线

11AB与平面1BCB所成角,Rt△1ABC中,由11111sin,2ANABNAB==得直线11AB与平面1BCB所成角为30.试题解析:（Ⅰ）证明:如图,连接1AC,在△1BCB中,因为E和F分别是BC,1BB的中点,所以11ABN,又因为EF平面11AB

BA,所以EF∥平面11ABBA.（Ⅱ）因为AB=AC,E为BC中点,所以AEBC⊥,因为1AN⊥平面ABC,所以1AN⊥平面ABC,从而1BBAE^,又1130ABN=,所以⊥AE平面1BCB,又因为⊥AE平面1BCB

,所以平面11ABN平面1BCB.（Ⅲ）取1BC中点M和1AN中点N,连接1NEAA=,11AB因为N和E分别为1AN,BC中点,所以,,故,1ABBB⊥,所以,1ANAE=,又因为⊥AE平面1BCB,所以11AMB平面1BCB,从而1AEA^就是直线11AB与平

面1BCB所成角,在△中,可得AE=2,所以1ANAE==2,因为,所以又由,有,在Rt△中,可得,在Rt△1ABC中,11111sin,2ANABNAB==因此,所以,直线11AB与平面1BCB所成角为30.考点：本题主要考查空间中线面位置关系的证明,直线与平面所成的角等基

础知识,考查空间想象能力及推理论证能力.67．（2015·陕西·高考真题）如图1，在直角梯形CD中，D//C，D2=，C1==，D2=，是D的中点，是C与的交点．将沿折起到1的位置，如图2．（Ⅰ）

证明：CD⊥平面1C；（Ⅱ）若平面1⊥平面CD，求平面1C与平面1CD夹角的余弦值．【答案】（Ⅰ）证明见解析；（Ⅱ）63．【详解】试题分析：（Ⅰ）先证1⊥，C⊥，再可证⊥

平面1C，进而可证CD⊥平面1C；（Ⅱ）先建立空间直角坐标系，再算出平面1C和平面1CD的法向量，进而可得平面1C与平面1CD夹角的余弦值．试题解析：（Ⅰ）在图1中，因为C1==，D2=，是D的中点，D2

=，所以C⊥即在图2中，1⊥，C⊥从而⊥平面1AOC又CD//，所以CD⊥平面1AOC．（Ⅱ）由已知，平面1ABE⊥平面CD，又由（Ⅰ）知，1OA⊥，C⊥所以

1AOC为二面角1--CABE的平面角，所以1OC2A=．如图，以为原点，建立空间直角坐标系，因为11B=E=BC=ED=1AA，//BCED所以12222(,0,0),(,0,0),(0,0,),(0,,0),2

222BEAC−得22(,,0),22BC−122(0,,)22AC−，(2,0,0)CDBE==−．设平面1BCA的法向量1111(,,)nxyz=，平面1CDA的法向量2222(,,)nxyz=，平面1BCA与平面1CDA夹角为，则1110{0nBCnAC==

，得11110{0xyyz−+=−=，取1(1,1,1)n=，2210{0nCDnAC==，得2220{0xyz=−=，取2(0,1,1)n=，从而1226cos,332cosnn===，即平面1BC

A与平面1CDA夹角的余弦值为63．考点：1、线面垂直；2、二面角；3、空间直角坐标系；4、空间向量在立体几何中的应用．68．（2015·湖南·高考真题）如图，直三棱柱111ABCABC-的底面是边长为2的正三角形，,EF分别是1,BCCC的中点．（１）证明：平面AEF⊥

平面11BBCC；（２）若直线1AC与平面11AABB所成的角为45，求三棱锥FAEC−的体积．【答案】（Ⅰ）见解析；（Ⅱ）612.【详解】试题分析：（１）由面面垂直的判定定理很容易得结论；（２）所求三棱锥底面积容易求得，是本题转化为求三棱锥的高FC，利用直线1AC与平面11AABB所成的

角为，作出线面角，进而可求得的值，则可得的FC长．试题解析：（1）如图，因为三棱柱111ABCABC-是直三棱柱，所以1⊥，又是正三角形C的边C的中点，所以C⊥又1C=

，因此⊥平面11CC而平面F，所以平面F⊥平面11CC（2）设的中点为D，连结1D,CD因为C是正三角形，所以CD⊥又三棱柱111ABCABC-是直三棱柱，所以1CD⊥因此CD⊥平面11，于是1CD为直线1C与

平面11所成的角，由题设，1CD45=，所以13DCD32===在1RtD中，2211DD312=−=−=，所以112FC22==故三棱锥FC−的体积C11326VFC332212S

===考点：直线与平面垂直的判定定理；直线与平面所成的角；几何体的体积．69．（2015·湖南·高考真题）如图，已知四棱台1111ABCDABCD−的上、下底面分别是边长为3和6的正方形，16AA=，且1AA⊥底面ABCD，点,PQ分别在棱1,DDBC上．（1）若P是1DD的中

点，证明：1ABPQ⊥；（2）若//PQ平面11ABBA，二面角PQDA−−的余弦值为37，求四面体ADPQ的体积．【答案】（1）见解析（2）24V=【详解】根据已知条件知AB，AD，1AA三直线两两垂直，所以分别以这三直线为x，y，z轴，建立如图所示空间直角坐标系，则：

(0A，0，0)，(6B，0，0)，(0D，6，0)，1(0A，0，6)，1(3B，0，6)，1(0D，3，6)；Q在棱BC上，设(6Q，1y，0)，106y剟；（1）证明：若P是1DD的中点，则9(0,,3)2P；19(6,,3)2PQy=−−，

1(3,0,6)AB=；10ABPQ=；1ABPQ⊥；1ABPQ⊥；（2）设(0P，2y，2)z，2y，2[0z，6]，P在棱1DD上；1DPDD=，01剟；(0，26y−，2)(0z=，3−，6)；22636yz−=−=；221

22zy=−；(0P，2y，2122)y−；122(6,,212)PQyyy=−−；平面11ABBA的一个法向量为(0,6,0)AD=；//PQ平面11ABBA；126()0PQADyy=−=；12yy=；(6Q，2y，0

)；设平面PQD的法向量为(,,)nxyz=，则：226(212)06(6)0nPQxyznDQxyy=+−==+−=；2632yxzyz−==，取1z=，则26(,2,1)3yn−=；又平面AQD的一个法向量为1(0,0,6)AA=；又二

面角PQDA−−的余弦值为37；12263cos,766()53nAAy==−+；解得24y=，或28y=（舍去）；(0P，4，4)；三棱锥PADQ−的高为4，且166182ADQS==；1184243ADPQPADQVV−===四面体三棱锥．考点：1.空间

向量的运用；2.线面垂直的性质；3.空间几何体体积计算.【名师点睛】本题主要考查了线面垂直的性质以及空间几何体体积计算，属于中档题，由于空间向量工具的引入，使得立体几何问题除了常规的几何法之外，还可以考

虑利用向量工具来解决，因此有关立体几何的问题，可以建立空间直角坐标系，借助于向量知识来解决，在立体几何的线面关系中，中点是经常使用的一个特殊点，无论是试题本身的已知条件，还是在具体的解题中，通过找“中点”，连“中点”，即可出现平行

线而线线平行是平行关系的根本，在垂直关系的证明中线线垂直是核心，也可以根据已知的平面图形通过计算的方式证明线线垂直，也可以根据已知的垂直关系证明线线垂直.70．（2015·湖北·高考真题）《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称

之为鳖臑．如图，在阳马PABCD−中，侧棱PD⊥底面ABCD，且PDCD=，过棱PC的中点E，作EFPB⊥交PB于点F，连接,,,.DEDFBDBE（Ⅰ）证明：PBDEF⊥平面．试判断四面体DBEF是否为鳖臑，若

是，写出其每个面的直角（只需写出结论）；若不是，说明理由；（Ⅱ）若面DEF与面ABCD所成二面角的大小为π3，求DCBC的值．【答案】（Ⅰ）详见解析；（Ⅱ）．【详解】（解法1）（Ⅰ）因为PD⊥底面ABCD，所以PDBC⊥，由底面AB

CD为长方形，有BCCD⊥，而PDCDD=，所以．而DEPCD平面，所以BCDE⊥．又因为PDCD=，点E是PC的中点，所以DEPC⊥．而PCBCC=，所以DE⊥平面PBC．而PBPBC平面，所以PBDE⊥．又PBEF⊥，DEEFE=，所以PB⊥平面DEF．

由DE⊥平面PBC，PB⊥平面DEF，可知四面体BDEF的四个面都是直角三角形，即四面体BDEF是一个鳖臑，其四个面的直角分别为DEBDEF，，EFBDFB，．（Ⅱ）如图1，在面PBC内，延长

BC与FE交于点G，则DG是平面DEF与平面ABCD的交线．由（Ⅰ）知，PBDEF⊥平面，所以PBDG⊥．又因为PD⊥底面ABCD，所以PDDG⊥．而PDPBP=，所以DGPBD⊥平面．故BDF是面DEF与面ABCD所成二面角的平面角，设1PDDC==，BC=，有2

1BD=+，在Rt△PDB中,由DFPB⊥,得π3DPFFDB==,则2πtantan133BDDPFPD===+=,解得2=．所以12.2DCBC==故当面DEF与面ABCD所成二面角的大小为π3时，22DCBC=

．（解法2）（Ⅰ）如图2，以D为原点，射线,,DADCDP分别为,,xyz轴的正半轴，建立空间直角坐标系．设1PDDC==，BC=，则(0,0,0),(0,0,1),(,1,0),(0,1,0)DPBC，(,1,1)PB=−，点E是PC的中点，所以11(0,,)22E，，

于是0PBDE=，即PBDE⊥．又已知EFPB⊥，而DEEFE=，所以PBDEF⊥平面．因,0DEPC=,则DEPC⊥,所以．由DE⊥平面PBC，PB⊥平面DEF，可知四面体BDEF的四个面都是直角三角形，即四面体BDEF是一个鳖臑，其四个面的直角分别为DEBDEF，，EFBDFB

，．（Ⅱ）由PDABCD⊥平面，所以是平面ABCD的一个法向量；由（Ⅰ）知，PBDEF⊥平面，所以是平面DEF的一个法向量．若面DEF与面ABCD所成二面角的大小为π3，则2π11cos322BPDPB

PDP===+，解得2=．所以12.2DCBC==故当面DEF与面ABCD所成二面角的大小为π3时，22DCBC=．考点：四棱锥的性质，线、面垂直的性质与判定，二面角．71．（2015·福建·高考真题）如图，AB是圆O的直径，点C是圆

O上异于,AB的点，垂直于圆所在的平面，且1==．（Ⅰ）若D为线段AC的中点，求证C⊥平面D；（Ⅱ）求三棱锥−PABC体积的最大值；（Ⅲ）若2BC=，点E在线段PB上，求CEOE+的最小值．【答案】

（Ⅰ）详见解析；（Ⅱ）13；（Ⅲ）262+．【详解】（Ⅰ）在C中，因为C=，D为C的中点，所以CD⊥．又垂直于圆所在的平面，所以C⊥．因为D=，所以C⊥平面D．（Ⅱ）因

为点C在圆上，所以当C⊥时，C到的距离最大，且最大值为1．又2=，所以C面积的最大值为12112=．又因为三棱锥C−的高1=，故三棱锥C−体积的最大值为111133=．（Ⅲ）在中，1==，90=，所以22112

=+=．同理C2=，所以CC==．在三棱锥C−中，将侧面C绕旋转至平面C，使之与平面共面，如图所示．当，，C共线时，C+取得最小值．又因为=，CC=，所以C垂直平分，即为中点．从而2626222CC+=+

=+=，亦即C+的最小值为262+．考点：1、直线和平面垂直的判定；2、三棱锥体积．72．（2015·北京·高考真题）如图，在三棱锥VC−中，平面V⊥平面C，V为等边三角形，CC⊥且CC2==，，分别为，V的中点

．(1)求证：V//平面C；(2)求证：平面C⊥平面V；(3)求三棱锥VC−的体积．【答案】（1）见解析；（2）见解析；（3）33.【详解】试题分析：（Ⅰ）利用三角形的中位线得出OM∥VB，利用线面平行的判定定理证明VB∥平面MOC

；（Ⅱ）证明OC⊥平面VAB，即可证明平面MOC⊥平面VAB；（Ⅲ）利用等体积法求三棱锥A-MOC的体积即可试题解析：（Ⅰ）证明：∵O，M分别为AB，VA的中点，∴OM∥VB，∵VB⊄平面MOC，OM⊂平面MOC，∴VB∥平面MOC；（Ⅱ）证明：∵AC=BC，O为AB的中点，∴OC

⊥AB，又∵平面VAB⊥平面ABC，平面ABC∩平面VAB=AB，且OC⊂平面ABC，∴OC⊥平面VAB，∵OC⊂平面MOC，∴平面MOC⊥平面VAB（Ⅲ）在等腰直角三角形ACB中，2ACBC==，所以2,1ABOC==.所以等边三角形V的面积3VABS=.

又因为OC⊥平面V，所以三棱锥CV−的体积等于1333VABOCS=.又因为三棱锥VC−的体积与三棱锥CV−的体积相等，所以三棱锥VC−的体积为33.考点：平面与平面垂直的判定；直线与

平面平行的判定；用向量证明平行73．（2015·北京·高考真题）如图，在四棱锥AEFCB−中，AEF△为等边三角形，平面AEF⊥平面EFCB，EFBC∥，4BC=，2EFa=，60EBCFCB==，O为EF的中点．（1）求证：A

OBE⊥．（2）求二面角FAEB−−的余弦值．（3）若BE⊥平面AOC，求a的值．【答案】（1）见解析；（2）余弦为55−；（2）43a=.【详解】试题分析：（1）要证AOBE⊥，可以先证明AO垂直于BE所在的平面E

FCB；（2）可以用向量法解决，取CB的中点D，连接OD，以O为原点，分别以OEODOA、、为xyz、、轴建立空间直角坐标系，分别求出两平面AEF、平面AEB的法向量，并求出法向量的夹角的余弦值，进而得

到二面角FAEB−−的余弦值；（3）因为BE⊥平面AOC，只需BEOC⊥，利用0BEOC=即可求出a的值.试题解析：（1）由于平面AEF⊥平面EFCB，为等边三角形，O为EF的中点，则AOEF⊥，根据面面垂直性质定理，所以AO⊥平面EF

CB，又BE平面EFCB，则AOBE⊥．（2）取CB的中点D，连接OD，以O为原点，分别以OEODOA、、为xyz、、轴建立空间直角坐标系，，由于平面AEF与y轴垂直，则设平面AEF的法向量为，设平面AEB的法向量，则，二面角FAEB−−的余弦值12121215cos,55nnnnn

n−===−，由二面角FAEB−−为钝二面角，所以二面角FAEB−−的余弦值为55−．（3）有（1）知AO⊥平面EFCB，则AOBE⊥，若BE⊥平面AOC，只需BEOC⊥，，又()()2222330BEOCaa=−−+−=，解得2

a=或43a=，由于2a，则43a=．考点：1、线线垂直；2、线面垂直；3、二面角.【思路点晴】本题是一个有关线线垂直、线面垂直、二面角方面的综合性问题，解决本题的基本思路是：对于（1）要证AOBE⊥，可以先证明AO垂直于BE所在的平面；对于（3）在建立直角坐标系之后，解决问题的关键是要正确

求出平面AEF的法向量和平面AEB的法向量，之后再根据向量夹角的公式就可求出二面角FAEB−−的余弦值；对于（3）在前两问的基础上，只需由BEOC⊥即可求出a的值.考点03求空间中的线段长度、点面距的值及最值或范围1．（2024·全国甲卷·高考真题）如图，

//,//ABCDCDEF，2ABDEEFCF====，104,CDADBC===，AE23=,M为CD的中点.(1)证明：//EM平面BCF；(2)求点M到ADE的距离.【答案】(1)证明见详解；(2)61313【分析】（1）结合已知易证四边

形EFCM为平行四边形，可证//EMFC，进而得证；（2）先证明OA⊥平面EDM，结合等体积法MADEAEDMVV−−=即可求解.【详解】（1）由题意得，//EFMC，且EFMC=，所以四边形EFCM是平行四边形，所以/

/EMFC，又CF平面,BCFEM平面BCF，所以//EM平面BCF；（2）取DM的中点O，连接OA，OE，因为//ABMC，且ABMC=，所以四边形AMCB是平行四边形，所以10AMBC==，又10AD=，故ADM△是等腰三角形，同理EDM△是等腰三角形，可得2

222,,3,322DMDMOADMOEDMOAADOEED⊥⊥=−==−=，又AE23=，所以222OAOEAE+=，故OAOE⊥.又,,,OADMOEDMOOEDM⊥=平

面EDM，所以OA⊥平面EDM，易知12332EDMS==.在ADEV中，412103cos42223DEA+−==，所以1311339sin,2234242DEADEAS===.设点M到

平面ADE的距离为d，由MADEAEDMVV−−=，得1133ADEEDMSdSOA=，得61313d=，故点M到平面ADE的距离为61313.2．（2024·天津·高考真题）已知四棱柱1111ABCDABCD−中，底面

ABCD为梯形，//ABCD，1AA⊥平面ABCD，ADAB⊥，其中12,1ABAAADDC====．N是11BC的中点，M是1DD的中点．(1)求证1//DN平面1CBM；(2)求平面1CBM与平面11BBCC的夹角余弦值；(3)求点B到平面1C

BM的距离．【答案】(1)证明见解析(2)22211(3)21111【分析】（1）取1CB中点P，连接NP，MP，借助中位线的性质与平行四边形性质定理可得1N//DMP，结合线面平行判定定理即可得证；（2

）建立适当空间直角坐标系，计算两平面的空间向量，再利用空间向量夹角公式计算即可得解；（3）借助空间中点到平面的距离公式计算即可得解.【详解】（1）取1CB中点P，连接NP，MP，由N是11BC的中点，故1//NPCC，且112NPCC=，由M是1DD的中点，故1111122DMDDCC==，且1

1//DMCC，则有1//DMNP、1DMNP=，故四边形1DMPN是平行四边形，故1//DNMP，又MP平面1CBM，1DN平面1CBM，故1//DN平面1CBM；（2）以A为原点建立如图所示空间直角坐标系，有

()0,0,0A、()2,0,0B、()12,0,2B、()0,1,1M、()1,1,0C、()11,1,2C，则有()11,1,2CB=−、()1,0,1CM=−、()10,0,2BB=，设平面1CBM与平面11BBCC的法向量分别为()111

,,mxyz=、()222,,nxyz=，则有111111200mCBxyzmCMxz=−+==−+=，1222122020nCBxyznBBz=−+===，分别取121xx==，则有13y=、11z=、21y=，20z=

，即()1,3,1m=、()1,1,0n=，则13222cos,1119111mnmnmn+===+++，故平面1CBM与平面11BBCC的夹角余弦值为22211；（3）由()10,0,2BB=，平面1CBM的法向量为()1,3,1m=，则有122111119

1BBmm==++，即点B到平面1CBM的距离为21111.3．（2023·全国甲卷·高考真题）如图，在三棱柱111ABCABC-中，1AC⊥平面,90ABCACB=．(1)证明：平面11ACCA⊥平面11BBCC；(2)设11,2ABABAA==，

求四棱锥111ABBCC−的高．【答案】(1)证明见解析.(2)1【分析】(1)由1AC⊥平面ABC得1ACBC⊥，又因为ACBC⊥，可证BC⊥平面11ACCA，从而证得平面11ACCA⊥平面11BCCB；(2)过点1A作11AOCC⊥，可证四棱锥的高为1AO,由三角形全等可证1ACAC=，从

而证得O为1CC中点，设1ACACx==，由勾股定理可求出x，再由勾股定理即可求1AO.【详解】（1）证明：因为1AC⊥平面ABC，BC平面ABC,所以1ACBC⊥,又因为90ACB=，即ACBC⊥，1,ACAC平面1

1ACCA，1ACACC=,所以BC⊥平面11ACCA，又因为BC平面11BCCB,所以平面11ACCA⊥平面11BCCB.（2）如图，过点1A作11AOCC⊥，垂足为O.因为平面11ACCA⊥平面11BCCB，平面11ACCA平面11

1BCCBCC=，1AO平面11ACCA，所以1AO⊥平面11BCCB，所以四棱锥111ABBCC−的高为1AO.因为1AC⊥平面ABC，,ACBC平面ABC,所以1ACBC⊥,1ACAC⊥,又因为1AB

AB=，BC为公共边，所以ABC与1ABC全等，所以1ACAC=.设1ACACx==，则11ACx=，所以O为1CC中点，11112OCAA==,又因为1ACAC⊥,所以22211ACACAA+=,即2222xx+=，解得2x=，所以()22221111

211AOACOC=−=−=，所以四棱锥111ABBCC−的高为1．4．（2022·全国新Ⅰ卷·高考真题）如图，直三棱柱111ABCABC-的体积为4，1ABC的面积为22．(1)求A到平面1ABC的距离；(2)设D为1AC的中点，1AAAB=，平面1ABC⊥平面11AB

BA，求二面角ABDC−−的正弦值．【答案】(1)2(2)32【分析】（1）由等体积法运算即可得解；（2）由面面垂直的性质及判定可得BC⊥平面11ABBA，建立空间直角坐标系，利用空间向量法即可得解.【详解】（1）在直三

棱柱111ABCABC-中，设点A到平面1ABC的距离为h，则111111112211433333AABCAAABCAABCABBCCCBVShhVSAAV−−−======，解得2h=，所以点A到平面1ABC的距离为2；（2）取1AB的中点E,连接AE,如图，因为

1AAAB=，所以1AEAB⊥,又平面1ABC⊥平面11ABBA，平面1ABC平面111ABBAAB=，且AE平面11ABBA，所以⊥AE平面1ABC，在直三棱柱111ABCABC-中，1BB⊥平面ABC，由BC平面1

ABC，BC平面ABC可得AEBC⊥，1BBBC⊥，又1,AEBB平面11ABBA且相交，所以BC⊥平面11ABBA，所以1,,BCBABB两两垂直，以B为原点，建立空间直角坐标系，如图，由（1）得2AE=，所以12AAAB==，

122AB=，所以2BC=，则()()()()10,2,0,0,2,2,0,0,0,2,0,0AABC,所以1AC的中点()1,1,1D，则()1,1,1BD=，()()0,2,0,2,0,0BABC==,设平面ABD的一个法向量(),,mxyz=，则020mB

DxyzmBAy=++===，可取()1,0,1m=−，设平面BDC的一个法向量(),,nabc=，则020nBDabcnBCa=++===，可取()0,1,1n=−r，则11cos,222mnmnmn===，所以二面角ABDC−−的正弦值为2

13122−=.5．（2021·全国乙卷·高考真题）如图，四棱锥PABCD−的底面是矩形，PD⊥底面ABCD，1PDDC==，M为BC的中点，且PBAM⊥．（1）求BC；（2）求二面角APMB−−的正弦值．【答案】（1）2；（2）70

14【分析】（1）以点D为坐标原点，DA、DC、DP所在直线分别为x、y、z轴建立空间直角坐标系，设2BCa=，由已知条件得出0PBAM=，求出a的值，即可得出BC的长；（2）求出平面PAM、PBM的法向量，利用空间向量法结合同角三角函数的基本关系可求得结果.【详解】（1

）[方法一]：空间坐标系+空间向量法PD⊥平面ABCD，四边形ABCD为矩形，不妨以点D为坐标原点，DA、DC、DP所在直线分别为x、y、z轴建立如下图所示的空间直角坐标系Dxyz−，设2BCa=，则()0,0,0D、()0,0,1P、()2,1,0Ba、(),1,0Ma、()2,0,0A

a，则()2,1,1PBa=−，(),1,0AMa=−，PBAM⊥，则2210PBAMa=−+=，解得22a=，故22BCa==；[方法二]【最优解】：几何法+相似三角形法如图，连结BD．因为PD⊥底面ABCD，且AM底面ABCD，

所以PDAM⊥．又因为PBAM⊥，PBPDP=，所以AM⊥平面PBD．又BD平面PBD，所以AMBD⊥．从而90ADBDAM+=．因为90+=MABDAM，所以=MABADB．所以∽ADBBAM，于是=ADBAABBM．所以2112BC=．所以2BC=．[方法三

]：几何法+三角形面积法如图，联结BD交AM于点N．由[方法二]知⊥AMDB．在矩形ABCD中，有∽DANBMN，所以2==ANDAMNBM，即23ANAM=．令2(0)=BCtt，因为M为BC的中点，则BMt=

，241=+DBt，21=+AMt．由1122==DABSDAABDBAN，得221241123=++ttt，解得212t=，所以22==BCt．（2）[方法一]【最优解】：空间坐标系+空间向量法设平面PAM的法向量

为()111,,mxyz=，则2,1,02AM=−，()2,0,1AP=−，由111120220mAMxymAPxz=−+==−+=，取12x=，可得()2,1,2m=，设平面PBM的法向量为()222,,

nxyz=，2,0,02BM=−，()2,1,1BP=−−，由222220220nBMxnBPxyz=−==−−+=，取21y=，可得()0,1,1n=，3314cos,1472mnmnmn===，所以，270sin,1cos,14mnmn=−=，因

此，二面角APMB−−的正弦值为7014.[方法二]：构造长方体法+等体积法如图，构造长方体1111ABCDABCD−，联结11,ABAB，交点记为H，由于11ABAB⊥，1ABBC⊥，所以AH⊥平面11ABCD．过H作1DM的垂

线，垂足记为G．联结AG，由三垂线定理可知1⊥AGDM，故AGH为二面角APMB−−的平面角．易证四边形11ABCD是边长为2的正方形，联结1DH，HM．111111111,2DHMDHMDAHHBMMCDABCDSDMHGSSSSS==−−−正方形，由等积法解得31010=HG．在

RtAHG中，2310,210==AHHG，由勾股定理求得355=AG．所以，70sin14AHAGHAG==，即二面角APMB−−的正弦值为7014．【整体点评】（1）方法一利用空坐标系和空间向量的坐标运算求解；方法二利

用线面垂直的判定定理，结合三角形相似进行计算求解，运算简洁，为最优解；方法三主要是在几何证明的基础上，利用三角形等面积方法求得.（2）方法一，利用空间坐标系和空间向量方法计算求解二面角问题是常用的方法，思路清晰，

运算简洁，为最优解；方法二采用构造长方体方法+等体积转化法，技巧性较强，需注意进行严格的论证.6．（2019·全国·高考真题）如图，直四棱柱ABCD–A1B1C1D1的底面是菱形，AA1=4，AB=2，∠BAD=60°，E，M，N分别是BC，BB1，A1D的中

点.（1）证明：MN∥平面C1DE；（2）求点C到平面C1DE的距离．【答案】（1）见解析；（2）41717.【分析】（1）利用三角形中位线和11//ADBC可证得//MEND，证得四边形MNDE为平行四边形，进而证得//MNDE，根据线面平行判定定理可证得结

论；（2）根据题意求得三棱锥1CCDE−的体积，再求出1CDE的面积，利用11CCDECCDEVV−−=求得点C到平面1CDE的距离，得到结果.【详解】（1）连接ME，1BCM，E分别为1BB，BC中点ME为1BBC的中位线1

//MEBC且112MEBC=又N为1AD中点，且11//ADBC1//NDBC且112NDBC=//MEND四边形MNDE为平行四边形//MNDE，又MN平面1CDE，DE平面1CDE//MN平面1CDE（2）在菱形ABCD中，E为BC中点，所以DEBC⊥，根据题意有3DE=

，117CE=，因为棱柱为直棱柱，所以有DE⊥平面11BCCB，所以1DEEC⊥，所以113172DECS=，设点C到平面1CDE的距离为d，根据题意有11CCDECCDEVV−−=，则有11113171343232d=，解得44171717d==，所

以点C到平面1CDE的距离为41717.【点睛】该题考查的是有关立体几何的问题，涉及到的知识点有线面平行的判定，点到平面的距离的求解，在解题的过程中，注意要熟记线面平行的判定定理的内容，注意平行线的寻找思路，再者就是利用等积法求点到平面的距离是文科生常考的内容.7．（2018·全国·高考真题）如图

，在三棱锥PABC−中，22ABBC==，4PAPBPCAC====，O为AC的中点．（1）证明：PO⊥平面ABC；（2）若点M在棱BC上，且2MCMB=，求点C到平面POM的距离．【答案】（1）证明见解析；（2）455．【分析】（1）连接OB，欲证PO⊥平面ABC，只

需证明,POACPOOB⊥⊥即可；（2）方法一：过点C作CHOM⊥，垂足为M，只需论证CH的长即为所求，再利用平面几何知识求解即可.【详解】（1）因为AP=CP=AC=4，O为AC的中点，所以OP⊥AC，且OP=23．连

结OB．因为AB=BC=22AC，222ABBCAC+=，所以△ABC为等腰直角三角形，且OB⊥AC，OB=12AC=2．由222OPOBPB+=知，OP⊥OB．由OP⊥OB，OP⊥AC，OBACO=，知PO⊥平面ABC．（2）［方法一］：【最优解】定义法作CH⊥

OM，垂足为H．又由（1）易知OP⊥平面ABC，从而OP⊥CH，所以CH⊥平面POM．故CH的长为点C到平面POM的距离．由题设可知OC=12AC=2，CM=23BC=423，∠ACB=45°．所以OM=253，CH

=sinOCMCACBOM=455．所以点C到平面POM的距离为455．［方法二］：等积法设C到平面POM的距离为h，由（1）知PO即为P到平面COM的距离，且POOM⊥．又23PO=，在OMC△中，2422,

,4533OCCMBCACB====，则由余弦定理得253OM=，则CPOMPCOMVV−−=，即1133POMCOMShSPO=△△，则221232453251252323COMPOMSPOhS===△△．即点C到平面POM的距离为455．［方法三］：向量法如图，

以O为原点，建立直角坐标系Oxyz，设(0,0,23)P，(2,0,0)B，(0,0,0)O，42,,033M，(0,2,0)C，(0,0,23)OP=，42,,033OM=，(0,2,0)OC=．设平面POM的一个法向量(,,)nxyz=，则23=0=042+=0=

033zOPnxyOMn，令1x=−，则(1,2,0)n=−，所以，点C到平面POM的距离为||455||nOCn=．【整体点评】（2）方法一：根据定义法求点到面的距离，是解决点面距问题的首选方法，特别是题目中含有面面垂直的条件，计算简单，是

该题的最优解；方法二：根据等积法求点到面的距离，也是解决点面距问题的常用方法；方法三：当题目中有较好的建系条件，利用向量法解决点面距，思想简单，过程稍繁．考点04求空间中的体积、表面积的值及最值或范围1．（2024·上海·高考真题）如图为正四棱锥,

PABCDO−为底面ABCD的中心．(1)若5,32APAD==，求POA绕PO旋转一周形成的几何体的体积；(2)若,APADE=为PB的中点，求直线BD与平面AEC所成角的大小．【答案】(1)12π(

2)π4【分析】（1）根据正四棱锥的数据，先算出直角三角形POA的边长，然后求圆锥的体积；（2）连接,,EAEOEC，可先证BE⊥平面ACE，根据线面角的定义得出所求角为BOE，然后结合题目数量关系求解.【详解】（1）正四棱锥满足且PO⊥平面ABCD，由AO平面ABCD，则POA

O⊥，又正四棱锥底面ABCD是正方形，由32=AD可得，3AO=，故224POPAAO=−=，根据圆锥的定义，POA绕PO旋转一周形成的几何体是以PO为轴，AO为底面半径的圆锥，即圆锥的高为4PO=，底面半径为3AO=，根据圆锥的体积公式，所得圆锥的体积是21π3412π3

=（2）连接,,EAEOEC，由题意结合正四棱锥的性质可知，每个侧面都是等边三角形，由E是PB中点，则,AEPBCEPB⊥⊥，又,,AECEEAECE=平面ACE，故PB⊥平面ACE，即BE⊥平面ACE，又BD平面ACE

O=，于是直线BD与平面AEC所成角的大小即为BOE，不妨设6APAD==，则32,3BOBE==，32sin232BOE==，又线面角的范围是π0,2，故π4BOE=.即为所求.2．（2023·全国乙

卷·高考真题）如图，在三棱锥−PABC中，ABBC⊥，2AB=，22BC=，6PBPC==，,,BPAPBC的中点分别为,,DEO，点F在AC上，BFAO⊥．(1)求证：EF//平面ADO；(2)若12

0POF=，求三棱锥−PABC的体积．【答案】(1)证明见解析(2)263【分析】（1）根据给定条件，证明四边形ODEF为平行四边形，再利用线面平行的判定推理作答.（2）作出并证明PM为棱锥的高，利用三棱锥的体积公式直接可求体积.【详解】（1）连接,DEOF，设AFtAC=

，则(1)BFBAAFtBAtBC=+=−+，12AOBABC=−+，BFAO⊥，则2211[(1)]()(1)4(1)4022BFAOtBAtBCBABCtBAtBCtt=−+−+=−+=−+=，解得12t=，则F为AC的中点，由,,,DEOF

分别为,,,PBPABCAC的中点，于是11//,,//,22DEABDEABOFABOFAB==，即,//DEOFDEOF=，则四边形ODEF为平行四边形，//,EFDOEFDO=，又EF平面,ADODO平面ADO

，所以//EF平面ADO.（2）过P作PM垂直FO的延长线交于点M，因为,PBPCO=是BC中点，所以POBC⊥，在RtPBO△中，16,22PBBOBC===，所以22622POPBOB=−=−=，因为,//ABBCOFAB⊥，

所以OFBC⊥，又POOFO=，,POOF平面POF，所以BC⊥平面POF，又PM平面POF，所以BCPM⊥，又BCFMO=，,BCFM平面ABC，所以PM⊥平面ABC，即三棱锥−PABC的高为

PM，因为120POF=，所以60POM=，所以3sin60232PMPO===，又112222222ABCSABBC===△，所以1126223333PABCABCVSPM−===△.3．（2022

·全国甲卷·高考真题）小明同学参加综合实践活动，设计了一个封闭的包装盒，包装盒如图所示：底面ABCD是边长为8（单位：cm）的正方形，,,,EABFBCGCDHDA均为正三角形，且它们所在的平面都与平面ABCD垂直．(1)证明：//EF平面ABCD；(2)求该包装盒的容积（不

计包装盒材料的厚度）．【答案】(1)证明见解析；(2)64033．【分析】（1）分别取,ABBC的中点,MN，连接MN，由平面知识可知,EMABFNBC⊥⊥，EMFN=，依题从而可证EM⊥平面ABCD，FN⊥平面ABCD，根据线面垂直的性质定理可知//EMFN，

即可知四边形EMNF为平行四边形，于是//EFMN，最后根据线面平行的判定定理即可证出；（2）再分别取,ADDC中点,KL，由（1）知，该几何体的体积等于长方体KMNLEFGH−的体积加上四棱锥BMNFE−体积的4倍，即可解

出．【详解】（1）如图所示：分别取,ABBC的中点,MN，连接MN，因为,EABFBC为全等的正三角形，所以,EMABFNBC⊥⊥，EMFN=，又平面EAB⊥平面ABCD，平面EAB平面ABCDAB=，E

M平面EAB，所以EM⊥平面ABCD，同理可得FN⊥平面ABCD，根据线面垂直的性质定理可知//EMFN，而EMFN=，所以四边形EMNF为平行四边形，所以//EFMN，又EF平面ABCD，MN平面ABCD，所以//E

F平面ABCD．（2）[方法一]：分割法一如图所示：分别取,ADDC中点,KL，由（1）知，//EFMN且EFMN=，同理有，//,HEKMHEKM=，//,HGKLHGKL=，//,GFLNGFLN=，由平面知识可知

，BDMN⊥，MNMK⊥，KMMNNLLK===，所以该几何体的体积等于长方体KMNLEFGH−的体积加上四棱锥BMNFE−体积的4倍．因为42MNNLLKKM====，8sin6043EM==，点B到平面MNFE的距离即为点B到直线M

N的距离d，22d=，所以该几何体的体积()2125664042434424322128333333V=+=+=．[方法二]：分割法二如图所示：连接AC,BD,交于O，连接OE,OF,OG,OH.则该几何体的体积等于四棱锥O-EFGH的体积加上三棱锥A-

OEH的4倍,再加上三棱锥E-OAB的四倍．容易求得，OE=OF=OG=OH=8,取EH的中点P，连接AP,OP.则EH垂直平面APO.由图可知，三角形APO,四棱锥O-EFGH与三棱锥E-OAB的高均为EM的长.所以该

几何体的体积()2111116403434244242434434242.332323V=++=4．（2022·全国乙卷·高考真题）如图，四面体ABCD中，,,ADCDADCDADBBDC⊥==，E为AC的中点．(1)证明：平面BED⊥平面ACD；(2)设2,

60ABBDACB===，点F在BD上，当AFC△的面积最小时，求三棱锥FABC−的体积．【答案】(1)证明详见解析(2)34【分析】（1）通过证明AC⊥平面BED来证得平面BED⊥平面ACD.（2）首先判断出三角形AFC的面积最小时F点的位置，然后求得F到平面ABC的距

离，从而求得三棱锥FABC−的体积.【详解】（1）由于ADCD=，E是AC的中点，所以ACDE⊥.由于ADCDBDBDADBCDB===，所以ADBCDB△△，所以ABCB=，故ACBE⊥，由于DEBEE=，,

DEBE平面BED，所以AC⊥平面BED，由于AC平面ACD，所以平面BED⊥平面ACD.（2）[方法一]：判别几何关系依题意2ABBDBC===，60ACB=，三角形ABC是等边三角形，所以2,1,3ACAECEBE====，由于,ADCDADCD=⊥，所以三角形ACD是等腰直角三角

形，所以1DE=.222DEBEBD+=，所以DEBE⊥，由于ACBEE=，,ACBE平面ABC，所以DE⊥平面ABC.由于ADBCDB△△，所以FBAFBC=，由于BFBFFBAFBCABCB===，所以FBAFBC，所以AFCF

=，所以EFAC⊥，由于12AFCSACEF=，所以当EF最短时，三角形AFC的面积最小过E作EFBD⊥，垂足为F，在RtBED△中，1122BEDEBDEF=，解得32EF=，所以223131,2222DF

BFDF=−==−=，所以34BFBD=过F作FHBE⊥，垂足为H，则//FHDE，所以FH⊥平面ABC，且34FHBFDEBD==，所以34FH=，所以111332333244FABCABCVSFH−===.[方法二]：等体积

转换ABBC=，60ACB=，2AB=ABC是边长为2的等边三角形，3BE=连接EFADBCDBAFCFEFACBEDEFBD=⊥⊥在中，当时，AFC面积最小222,,2,3,BEDEF2ADCDADCDACEACDEB

EBDBEEDBEDEEFBDBD⊥==+=⊥⊥==为中点DE=1若在中，223211333322228BEFBFBEEFSBFEF=−====1133323384FABCABEFCBEFBEFVVVSAC−−−=+===5．（2021·

全国新Ⅰ卷·高考真题）如图，在三棱锥ABCD−中，平面ABD⊥平面BCD，ABAD=，O为BD的中点.（1）证明：OACD⊥；（2）若OCD是边长为1的等边三角形，点E在棱AD上，2DEEA=，且二面角EBCD−−的大小为45，求三棱锥ABCD−的体积.【答案】(1)证明见解析；(2

)36.【分析】(1)由题意首先证得线面垂直，然后利用线面垂直的定义证明线线垂直即可；(2)方法二：利用几何关系找到二面角的平面角，然后结合相关的几何特征计算三棱锥的体积即可.【详解】（1）因为ABAD=，O是BD中点，所以OABD⊥，因为OA平面ABD，平面ABD⊥平面BC

D，且平面ABD平面BCDBD=，所以OA⊥平面BCD．因为CD平面BCD，所以OACD⊥.（2）[方法一]：通性通法—坐标法如图所示，以O为坐标原点，OA为z轴，OD为y轴，垂直OD且过O的直线为x轴，建立空间直角坐标系Oxy

z−，则31(,,0),(0,1,0),(0,1,0)22CDB−，设12(0,0,),(0,,)33AmEm,所以4233(0,,),(,,0)3322EBmBC=−−=，设(),,nxyz=r为平面EBC的法向量，则由00EBnBCn==可求得平面EBC的一个法向量为2

(3,1,)nm=−−．又平面BCD的一个法向量为()0,0,OAm=，所以222cos,244nOAmm−==+，解得1m=．又点C到平面ABD的距离为32，所以1133213226ABCDCABDVV−−===，所以三棱锥ABCD−的体积为36．[方法二]【最优解】：作出二面角的

平面角如图所示，作EGBD⊥，垂足为点G．作GFBC⊥，垂足为点F，连结EF，则OAEG∥．因为OA⊥平面BCD，所以EG⊥平面BCD，EFG为二面角EBCD−−的平面角．因为45EFG=，所以EGFG=．由

已知得1OBOD==，故1OBOC==．又30OBCOCB==，所以3BC=．因为24222,,,,133333GDGBFGCDEGOA======，11113322(11)1333226ABCDBCDBOCVSOSOAA−====．[方法三]：三面角公

式考虑三面角BEDC−，记EBD为，EBC为，30DBC=，记二面角EBCD−−为．据题意，得45=．对使用三面角的余弦公式，可得coscoscos30=，化简可得3coscos2=．①使用三面角的正弦公式，可得sinsinsin=，化简可得sin2

sin=．②将①②两式平方后相加，可得223cos2sin14+=，由此得221sincos4=，从而可得1tan2=．如图可知π(0,)2，即有1tan2=，根据三角形相似知，点G为OD的三等分点，即可得43BG=，结合的

正切值，可得2,13EGOA==从而可得三棱锥ABCD−的体积为36．【整体点评】(2)方法一：建立空间直角坐标系是解析几何中常用的方法，是此类题的通性通法，其好处在于将几何问题代数化，适合于复杂图形的处理；方法二：找到二面角的平面角是立体几何的基本

功，在找出二面角的同时可以对几何体的几何特征有更加深刻的认识，该法为本题的最优解.方法三：三面角公式是一个优美的公式，在很多题目的解析中灵活使用三面角公式可以使得问题更加简单、直观、迅速.6．（2021·全国甲卷·高考真题）已知直三

棱柱111ABCABC-中，侧面11AABB为正方形，2ABBC==，E，F分别为AC和1CC的中点，11BFAB⊥.（1）求三棱锥FEBC−的体积；（2）已知D为棱11AB上的点，证明：BFDE⊥.【答案】(1)13；(2)证明见解析.【分析】（1）先证明ABC为等腰直角三

角形，然后利用体积公式可得三棱锥的体积；（2）将所给的几何体进行补形，从而把线线垂直的问题转化为证明线面垂直，然后再由线面垂直可得题中的结论.【详解】（1）由于11BFAB⊥，11//ABAB，所以ABBF⊥，又AB⊥BB1，1BBBFB=，故AB⊥平面11BCCB，则ABBC⊥，ABC为

等腰直角三角形，111221222BCEABCSS===△△，11111333FEBCBCEVSCF−===△.（2）由（1）的结论可将几何体补形为一个棱长为2的正方体1111ABCMAB

CM−，如图所示，取棱,AMBC的中点,HG，连结11,,AHHGGB，正方形11BCCB中，,GF为中点，则1BFBG⊥，又111111,BFABABBGB⊥=，故BF⊥平面11ABGH，而DE平面11ABGH，从而BF⊥DE.【点睛】求三棱锥的体积时要注意三棱锥的每个面都可以

作为底面，例如三棱锥的三条侧棱两两垂直，我们就选择其中的一个侧面作为底面，另一条侧棱作为高来求体积．对于空间中垂直关系（线线、线面、面面）的证明经常进行等价转化.7．（2021·全国乙卷·高考真题）如图，四

棱锥PABCD−的底面是矩形，PD⊥底面ABCD，M为BC的中点，且PBAM⊥．（1）证明：平面PAM⊥平面PBD；（2）若1PDDC==，求四棱锥PABCD−的体积．【答案】（1）证明见解析；（2）23．【分析】（1）由PD⊥底面ABCD

可得PDAM⊥，又PBAM⊥，由线面垂直的判定定理可得AM⊥平面PBD，再根据面面垂直的判定定理即可证出平面PAM⊥平面PBD；（2）由（1）可知，AMBD⊥，由平面知识可知，~DABABM，由相似比可求出AD，再根据四棱

锥PABCD−的体积公式即可求出．【详解】（1）因为PD⊥底面ABCD，AM平面ABCD，所以PDAM⊥，又PBAM⊥，PBPDP=，所以AM⊥平面PBD，而AM平面PAM，所以平面PAM⊥平面PBD．（2）[方法一]：相似三角形法由（1）可知AMBD

⊥．于是∽ABDBMA，故=ADABABBM．因为1,,12===BMBCADBCAB，所以2112BC=，即2BC=．故四棱锥PABCD−的体积1233==VABBCPD．[方法二]：平面直角坐标系垂直垂直法

由（2）知⊥AMDB,所以1=−AMBDkk．建立如图所示的平面直角坐标系，设2(0)BCaa=．因为1DC=，所以(0,0)A，(1,0)B，(0,2)Da，()1,Ma．从而2020(2)211001−−==−=−=−−−AMBDaakkaaa．

所以22a=，即2DA=．下同方法一.[方法三]【最优解】：空间直角坐标系法建立如图所示的空间直角坐标系Dxyz−，设||=DAt，所以(0,0,0)D，(0,1,0)C，(0,0,1)P，(,0,0)At，(,1,0)

Bt．所以,1,02tM，(,1,1)PBt=−，,1,02tAM=−．所以2110(1)1022ttPBAMt=−++−=−+=．所以2t=，即||2=DA．下同方法一.[方法四]：空间向量

法由PBAM⊥，得0PBAM=．所以()0++=PDDAABAM．即0++=PDAMDAAMABAM．又PD⊥底面ABCD，AM在平面ABCD内，因此PDAM⊥，所以0=PDAM．所以0+

=DAAMABAM，由于四边形ABCD是矩形，根据数量积的几何意义，得221||||02−+=DAAB，即21||102−+=BC．所以||2BC=，即2BC=．下同方法一.【整体点评】(2)方法一利用相似三角形求出求出矩形的另一个边长，从而求

得该四棱锥的体积；方法二构建平面直角坐标系，利用直线垂直的条件得到矩形的另一个边长，从而求得该四棱锥的体积；方法三直接利用空间直角坐标系和空间向量的垂直的坐标运算求得矩形的另一个边长,为最常用的通性通法，为最优解；方法四利用空间向量转化求得矩形的另一边长.8．（

2020·全国·高考真题）如图，D为圆锥的顶点，O是圆锥底面的圆心，ABC是底面的内接正三角形，P为DO上一点，∠APC=90°．（1）证明：平面PAB⊥平面PAC；（2）设DO=2，圆锥的侧面积为3π，求三棱锥P−

ABC的体积.【答案】（1）证明见解析；（2）68.【分析】（1）根据已知可得PAPBPC==，进而有PAC△≌PBC，可得90APCBPC==，即PBPC⊥，从而证得PC⊥平面PAB，即可证得结论；（2）将已知条件转化为母线l和底

面半径r的关系，进而求出底面半径，由正弦定理，求出正三角形ABC边长，在等腰直角三角形APC中求出AP，在RtAPO中，求出PO，即可求出结论.【详解】（1）连接,,OAOBOC，D为圆锥顶点，O为底面圆心，OD⊥平面ABC，P在DO上，,OAOBOCPAPBPC====，ABC是圆内接正

三角形，ACBC=，PAC△≌PBC，90APCBPC==，即,PBPCPAPC⊥⊥，,PAPBPPC=⊥平面,PABPC平面PAC，平面PAB⊥平面PAC；（2）设圆锥的母线为l，底面半径为r，圆锥的侧面积为3,3rlr

l==，2222ODlr=−=，解得1,3rl==，2sin603ACr==，在等腰直角三角形APC中，2622APAC==，在RtPAO中，2262142POAPOA=−=−=，三棱锥−PABC的体积为11236333248PABCABCVPOS−===△.【点睛】本题考

查空间线、面位置关系，证明平面与平面垂直，求锥体的体积，注意空间垂直间的相互转化，考查逻辑推理、直观想象、数学计算能力，属于中档题.9．（2020·全国·高考真题）如图，已知三棱柱ABC–A1B1C1的底面是正三角形，侧面BB1C1C是矩形，M，N分别为BC，B1C1的中点，P为AM上一点．

过B1C1和P的平面交AB于E，交AC于F．（1）证明：AA1//MN，且平面A1AMN⊥平面EB1C1F；（2）设O为△A1B1C1的中心，若AO=AB=6，AO//平面EB1C1F，且∠MPN=π3，求四棱锥B–EB1C1F的体积．【答案】（1）证明见解析；（2）24.【分析】（1）由

,MN分别为BC，11BC的中点，1//MNCC，根据条件可得11//AABB，可证1MNAA//，要证平面11EBCF⊥平面1AAMN，只需证明EF⊥平面1AAMN即可；（2）根据已知条件求得11EBCFS四边形和M到PN的距离，根据锥

体体积公式，即可求得11BEBCFV−.【详解】（1）,MN分别为BC，11BC的中点，1//MNBB又11//AABB1//MNAA在等边ABC中，M为BC中点，则BCAM⊥又侧面11BBCC为矩形，1BCBB⊥1//MNBBMNB

C⊥由MNAMM=，,MNAM平面1AAMNBC⊥平面1AAMN又11//BCBC，且11BC平面ABC，BC平面ABC，11//BC平面ABC又11BC平面11EBCF，且平面11EBCF平面

ABCEF=11//BCEF//EFBC又BC⊥平面1AAMNEF⊥平面1AAMNEF平面11EBCF平面11EBCF⊥平面1AAMN（2）过M作PN垂线，交点为H，画出图形，如图//AO平面11EBCFAO平面1AAMN，平面1AAMN平面11EBCFNP=/

/AONP又//NOAP6AONP==O为111ABC△的中心.1111sin606sin60333ONAC===故：3ONAP==，则333AMAP==，平面11EBCF⊥平面1AAMN，平面11EBCF平面1AAMNNP=，MH平面1AAMNMH⊥平面11E

BCF又在等边ABC中EFAPBCAM=即36233APBCEFAM===由（1）知，四边形11EBCF为梯形四边形11EBCF的面积为：111126=62422EBCFEFBCSNP++==四边形1111

13BEBCFEBCFVSh−=四边形，h为M到PN的距离23sin603MH==，1243243V==.【点睛】本题主要考查了证明线线平行和面面垂直，及其求四棱锥的体积，解题关键是掌握面面垂直转为求证线面垂直的证法和棱锥的体积公式，考查了分析能力和空间想象能力，属于中档题.1

0．（2019·全国·高考真题）图1是由矩形,ADEBRtABC和菱形BFGC组成的一个平面图形，其中1,2ABBEBF===，60FBC=，将其沿,ABBC折起使得BE与BF重合，连结DG，如图2.（1

）证明图2中的,,,ACGD四点共面，且平面ABC⊥平面BCGE；（2）求图2中的四边形ACGD的面积.【答案】(1)见详解；(2)4.【分析】(1)因为折纸和粘合不改变矩形ABED，RtABC和菱形BFGC内部的夹角，所以//ADBE，//B

FCG依然成立，又因E和F粘在一起，所以得证.因为AB是平面BCGE垂线，所以易证.(2)欲求四边形ACGD的面积，需求出CG所对应的高，然后乘以CG即可．【详解】(1)证：//ADBE，//BFCG，又因为E和F粘在一起.//ADCG，A，C，G，D四点共面.又,ABB

EABBC⊥⊥.AB⊥平面BCGE，AB平面ABC，平面ABC⊥平面BCGE，得证.(2)取CG的中点M，连结,EMDM.因为//ABDE，AB⊥平面BCGE，所以DE⊥平面BCGE，故DECG⊥，由已知，四边形BCGE是菱

形，且60EBC=得EMCG⊥，故CG⊥平面DEM．因此DMCG⊥．在RtDEM△中，DE=1，3EM=，故2DM=．所以四边形ACGD的面积为4.【点睛】很新颖的立体几何考题．首先是多面体粘合问题，考查考生在粘合过程中哪些量是不变的．再者粘合后的多面体不是直棱柱，最后将求四边形

ACGD的面积考查考生的空间想象能力.11．（2019·全国·高考真题）如图，长方体ABCD–A1B1C1D1的底面ABCD是正方形，点E在棱AA1上，BE⊥EC1.（1）证明：BE⊥平面EB1C1；（2）若AE=A1E，AB=3，求四棱锥11EBBCC−的体积．【答案】（1）见详

解；（2）18【分析】（1）先由长方体得，11BC⊥平面11AABB，得到11BCBE⊥，再由1BEEC⊥，根据线面垂直的判定定理，即可证明结论成立；（2）先设长方体侧棱长为2a，根据题中条件求出3a=；再取1BB中点F，连结EF，证明EF⊥平面11BBCC，根据四棱锥的体积

公式，即可求出结果.【详解】（1）因为在长方体1111ABCDABCD−中，11BC⊥平面11AABB；BE平面11AABB，所以11BCBE⊥，又1BEEC⊥，1111BCECC=，且1EC平面11EBC，11BC平

面11EBC，所以BE⊥平面11EBC；（2）[方法一]【利用体积公式计算体积】如图6，设长方体的侧棱长为2a，则1AEAEa==．由（1）可得1EBBE⊥．所以22211EBBEBB+=，即2212BEBB=．又3AB=，所以222122AEABBB+=

，即222184aa+=，解得3a=．取1BB中点F，联结EF，因为1AEAE=，则EFAB∥，所以EF⊥平面11BBCC，从而四棱锥11EBBCC−的体积：11111133EBBCCBBCCVSEFBCBB−==矩形136318

3EF==．[方法二]【最优解：利用不同几何体之间体积的比例关系计算体积】取1BB的中点F，联结EF．由（Ⅰ）可知1BEEB⊥，所以1113,62EFBBABBB====．故11113361833EBBCCVV−===长方体．【整体点评】(2)方法一：利用体积公式计算体积

需要同时计算底面积和高，是计算体积的传统方法；方法二：利用不同几何体之间的比例关系计算体积是一种方便有效快速的计算体积的方法，核心思想为等价转化.12．（2018·全国·高考真题）如图，在平行四边形ABCM中，3A

BAC==，90ACM=，以AC为折痕将△ACM折起，使点M到达点D的位置，且ABDA⊥．（1）证明：平面ACD⊥平面ABC；（2）Q为线段AD上一点，P为线段BC上一点，且23BPDQDA==，求三棱锥QABP−的体积．【答案】(1)证明见解析；(2)1.

【分析】(1)根据题意可得BAAC⊥，又BA⊥AD，利用线面垂直的判定定理证得AB⊥平面ACD，再根据面面垂直的判定定理即可证得；(2)方法一：根据平面知识求出ABPS，再求得三棱锥的高，即可根据三棱锥的体积公式求出.【详解】（1）由已知可得，BAC=90°，BAAC⊥

．又BA⊥AD，且ACADA=，所以AB⊥平面ACD．又AB平面ABC，所以平面ACD⊥平面ABC．（2）［方法一］：定义法由已知可得，DC=CM=AB=3，DA=32．又23BPDQDA==，所以=22BP．作QE⊥A

C，垂足为E，则QE=13DC．由已知及（1）可得DC⊥平面ABC，所以QE⊥平面ABC，QE=1．因此，三棱锥QABP−的体积为1111322sin451332QABPABPVQES−===．［方法二

］：转化法由（1）知，DCAB⊥，又,DCCAABCAA⊥=，所以DC⊥平面ABC，则1932DABCABCVSDC−==△．因为21,33DQDAAQDA==，所以1332QABCDABCVV−−==．因为2233BPDABC==，所以213QABPQAB

CVV−−==．【整体点评】（2）方法一：根据三棱锥的体积公式求底面积和高，是求三棱锥体积的通性通法；方法二：根据题目的等量关系转化为求易求的三棱锥体积，也是求三棱锥体积的通性通法．13．（2017·上海·高考真题）如图，直三棱柱111ABCABC-的底面为直角三角形，两

直角边AB和AC的长分别为4和2，侧棱1AA的长为5.（1）求三棱柱111ABCABC-的体积；（2）设M是BC中点，求直线1AM与平面ABC所成角的大小.【答案】（1）20;（2）arctan5【分析】（1）三棱柱111ABCABC−的体积11ABC

VSAAACAA=，由此能求出结果；（2）连结1,AMAMA是直线1AM与平面ABC所成角，由此能求出直线1AM与平面ABC所成角的大小.【详解】解：（1）∵直三棱柱ABC﹣A1B1C1的底面为直角三角形

，两直角边AB和AC的长分别为4和2，侧棱AA1的长为5．∴三棱柱ABC﹣A1B1C1的体积：V＝S△ABC×AA1112ABACAA=14252==20．（2）连结AM，∵直三棱柱ABC﹣

A1B1C1的底面为直角三角形，两直角边AB和AC的长分别为4和2，侧棱AA1的长为5，M是BC中点，∴AA1⊥底面ABC，AM11164522BC==+=，∴∠A1MA是直线A1M与平面ABC所成角，tan∠A1MA1555AAAM===

，∴直线A1M与平面ABC所成角的大小为arctan5．【点睛】本题考查三棱柱的体积的求法，考查线面角的大小的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查推理论证能力、运算求解能力、空间想象能力，考查化归与转化思想、函数与方程思想、数形结合思想，是中档题．14．（201

7·全国·高考真题）如图，在四棱锥PABCD−中，ABCD∥，且90BAPCDP==.（1）证明：平面PAB⊥平面PAD；（2）若PAPDABDC===，90APD=，且四棱锥PABCD−的体积为

83，求该四棱锥的侧面积．【答案】（1）证明见解析；（2）623+.【详解】试题分析：（1）由90BAPCDP==，得ABAP⊥，CDPD⊥．从而得ABPD⊥，进而而AB⊥平面PAD，由面面垂直的判定定

理可得平面PAB⊥平面PAD；（2）设PAPDABDCa====，取AD中点O，连结PO，则PO⊥底面ABCD，且22,2ADaPOa==，由四棱锥PABCD−的体积为83，求出2a=，由此能求出该四棱锥的侧面积.试题解析：（1）由已知90BAP

CDP==，得ABAP⊥，CDPD⊥．由于ABCD∥，故ABPD⊥，从而AB⊥平面PAD．又AB平面PAB，所以平面PAB⊥平面PAD．（2）在平面PAD内作PEAD⊥，垂足为E．由（1）知，AB⊥面PAD，故ABPE⊥，可得PE⊥平面ABCD．设ABx=，则由已知可

得2ADx=，22PEx=．故四棱锥PABCD−的体积31133PABCDVABADPEx−==．由题设得31833x=，故2x=．从而2PAPD==，22ADBC==，22PBPC==．可得四棱锥PABCD−的侧面积为111222PAPD

PAABPDDC++21sin606232BC+=+．15．（2017·北京·高考真题）如图，在三棱锥P－ABC中，PA⊥AB，PA⊥BC，AB⊥BC，PA＝AB＝BC＝2，D为线段AC的中点，E为线段PC上一点.(1)求证：PA⊥BD；(2)求证：平面BDE⊥平面PAC；(3)当PA∥平

面BDE时，求三棱锥E－BCD的体积．【答案】（1）证明见解析；（2）证明见解析；（3）13【详解】试题分析：（Ⅰ）要证明线线垂直，一般转化为证明线面垂直；（Ⅱ）要证明面面垂直，一般转化为证明线面垂直、线线垂直；（Ⅲ）由1

3BCDVSDE=即可求解.试题解析:（I）因为PAAB⊥，PABC⊥，所以PA⊥平面ABC，又因为BD平面ABC，所以PABD⊥.（II）因为ABBC=，D为AC中点，所以BDAC⊥，由（I）知，PABD⊥，所以BD⊥平面PAC.所以平面BDE⊥平面PA

C.（III）因为PA平面BDE，平面PAC平面BDEDE=，所以PADE.因为D为AC的中点，所以112DEPA==，2BDDC==.由（I）知，PA⊥平面ABC，所以DE⊥平面PAC.所以三棱锥EBCD−的体积1163VBDDCDE==.【

名师点睛】线线、线面的位置关系以及证明是高考的重点内容，而其中证明线面垂直又是重点和热点，要证明线面垂直，根据判定定理可转化为证明线与平面内的两条相交直线垂直，也可根据性质定理转化为证明面面垂直.16．（2017·全国·高考真题）四棱锥PABCD−中，侧面PAD为等边三角形且垂

直于底面ABCD,01,90.2ABBCADBADABC====（1）证明：直线//BC平面PAD;（2）若△PCD面积为27，求四棱锥PABCD−的体积.【答案】（Ⅰ）见解析（Ⅱ）43【分析】试题分析：证明线面平有两种思路，一是寻求线线平行，二是寻求面面平行；取AD中点M，由于平面PAD为

等边三角形，则PMAD⊥，利用面面垂直的性质定理可推出PM⊥底面ABCD，设BCx=，表示相关的长度，利用PCD的面积为27，求出四棱锥的体积.试题解析：（1）在平面内，因为,所以又平面平面故平面（2）取的中点，连接由及得四边形为正方形，则.因为侧面为等边三角形且

垂直于底面，平面平面，所以底面因为底面，所以,设，则，取的中点，连接，则,所以，因为的面积为，所以，解得（舍去），于是所以四棱锥的体积【详解】17．（2016·江苏·高考真题）现需要设计一个仓库，它由上下两部分组成，上部分的形状是正四棱

锥1111PABCD−，下部分的形状是正四棱柱1111ABCDABCD−（如图所示），并要求正四棱柱的高1OO是正四棱锥的高1PO的4倍.（1）若16,2,ABmPOm==则仓库的容积是多少？（2）若正四棱锥的侧棱长为6m，则当1PO为多少时，仓库的

容积最大？【答案】（1）312（2）123PO=【详解】试题分析：（1）明确柱体与锥体积公式的区别，分别代入对应公式求解；（2）先根据体积关系建立函数解析式，()()32636063VVVhhh=+=−锥柱，然后利用导数求其最值.试题解析：解：（1）由PO1=2知OO1=4PO1=

8.因为A1B1=AB=6，所以正四棱锥P-A1B1C1D1的体积()22311111=6224m;33VABPO==锥正四棱柱ABCD-A1B1C1D1的体积()2231=68288m.VABOO==柱所以仓库的容积V=V锥+V柱=24+288=312（m3）.（2）设A1

B1=a（m），PO1=h（m），则0<h<6，OO1=4h.连结O1B1.因为在Rt11POB中，2221111OBPOPB，+=所以222362ah+=（），即()22236.ah=−于是仓库的容积()()22231132643606333VVVahahahhhh=+=+==−柱

锥，从而()()2226'36326123Vhh=−=−.令'0V=，得23h=或23h=−（舍）.当023h时，'0V，V是单调增函数；当236h时，'0V，V是单调减函数.故23h=时，V取得极大值，也是最大值.因此，当123PO=m时

，仓库的容积最大.【考点】函数的概念、导数的应用、棱柱和棱锥的体积【名师点睛】对应用题的训练，一般从读题、审题、剖析题目、寻找切入点等方面进行强化，注重培养将文字语言转化为数学语言的能力，强化构建数学模型的几种

方法.而江苏高考的应用题往往需结合导数知识解决相应的最值问题，因此掌握利用导数求最值方法是一项基本要求，需熟练掌握.18．（2016·全国·高考真题）如图，菱形ABCD的对角线AC与BD交于点O，点,EF分别在,ADCD上

，,AECFEF=交BD于点H，将DEF沿EF折起到DEF的位置.（Ⅰ）证明：ACHD⊥；（Ⅱ)若55,6,,224ABACAEOD====，求五棱锥DABCFE−的体积.【答案】（Ⅰ）详见解析；（Ⅱ）2322.【详解】试题分析：（1）由已知得，,ACBDA

DCD⊥=，AECF=AECFADCD=//ACEF,⊥⊥EFHDEFHDACHD⊥；（2）由//EFAC14OHAEDOAD==，由5,6ABAC==224DOBOABAO==−=1,3OHDHDH===()2222

2219ODOHDH+=+==ODOH⊥，可证OD⊥平面ABC．又由EFDHACDO=得92EF=五边形ABCFE的面积1682S=19693224−=以五棱锥DABCEF−体积16923222342V==．

试题解析：（1）由已知得，,ACBDADCD⊥=，又由AECF=得AECFADCD=，故//ACEF，由此得,⊥⊥EFHDEFHD，所以ACHD⊥．（2）由//EFAC得14OHAEDOAD==，由5,6AB

AC==得224DOBOABAO==−=，所以1,3OHDHDH===，于是()22222219ODOHDH+=+==，故ODOH⊥，由（1）知ACHD⊥，又,⊥=ACBDBDHDH，所以AC⊥平面B

HD，于是ACOD⊥，又由,⊥=ODOHACOHO，所以，OD⊥平面ABC．又由EFDHACDO=得92EF=．五边形ABCFE的面积119696832224S=−=．所以五棱锥DABCEF−体积16923222342V==．考点：1、线线

垂直；2、锥体的体积.19．（2016·上海·高考真题）将边长为1的正方形11AAOO（及其内部）绕1OO旋转一周形成圆柱，如图，AC长为23，11AB长为3，其中1B与C在平面11AAOO的同侧.(1)求三棱锥111COAB−的体积；(2)求异面直线1BC

与1AA所成的角的大小.【答案】(1)312(2)4.【详解】试题分析：（1）由题意可知，圆柱的高1h=，底面半径1r=，1113=，再由三角形面积公式计算111S后即得.（2）设过点1的母线与下底面交于点，根据11//，知1CΒΒ或其补角为直线1

ΒC与1所成的角，再结合题设条件确定π3CΟΒ=，1CΒ=．得出1π4CΒΒ=即可．试题解析：（1）由题意可知，圆柱的高1h=，底面半径1r=．由11AB的长为π3，可知1113=．111111111113

sin24ΟΑΒSΟΑΟΒAΟΒ==△，11111113V312COABSh−==．（2）设过点1的母线与下底面交于点，则11//，所以1CΒΒ或其补角为直线1ΒC与1所成的角．由AC长为2π3，可知2π3ΑΟC=，又111π3ΑΟΒΑΟΒ==，

所以π3CΟΒ=，从而CΟΒ△为等边三角形，得1CΒ=．因为1⊥平面ΑΟC，所以1ΒΒCΒ⊥．在1CΒΒ△中，因为1π2ΒΒC=，1CΒ=，11=，所以1π4CΒΒ=，从而直线1ΒC与1所成的角的大小为π4．

【考点】几何体的体积、空间角【名师点睛】此类题目是立体几何中的常见问题.解答本题时，关键在于能利用直线与直线、直线与平面、平面与平面位置关系的相互转化，将空间问题转化成平面问题.立体几何中的角与距离的计算问题，往往可以利用几何法、空间向量方法求解，应根据题目条件，灵活选择方法.本题能较好地

考查考生的空间想象能力、逻辑推理能力、转化与化归思想及基本运算能力等.20．（2016·上海·高考真题）将边长为1的正方形AA1O1O（及其内部）绕OO1旋转一周形成圆柱，如图，AC长为56，11AB长为3

，其中B1与C在平面AA1O1O的同侧．（1）求圆柱的体积与侧面积；（2）求异面直线O1B1与OC所成的角的大小．【答案】（1）,2；（2）2．【详解】（1）由题意可知，圆柱的母线长1l=，底面半径1r=．圆柱的体积2211Vrl==

=，圆柱的侧面积22112Srl===．（2）设过点B1的母线与下底面交于点B，则11//OBOB，所以COB或其补角为11OB与OC所成的角．由11AB长为3，可知1113AOBAOB==，由AC长为56，可知5π6AOC=

，2COBAOCAOB=−=，所以异面直线11OB与OC所成的角的大小为2．21．（2016·全国·高考真题）如图，四棱锥PABCD−中，PA⊥平面ABCD，ADBC∥，3ABADAC===，4PABC==，M为线段AD上一点，2AMMD=，N为P

C的中点．（I）证明MN∥平面PAB；（II）求四面体NBCM−的体积.【答案】(Ⅰ)证明见解析；(Ⅱ)453.【详解】试题分析：（Ⅰ）取PB的中点T，然后结合条件中的数据证明四边形AMNT为平行四边形，从而得到MNAT∥，由此结合线面平行的判断定理可证；（Ⅱ）由条件可知四面体N-BCM的

高，即点N到底面的距离为棱PA的一半，由此可顺利求得结果．试题解析：（Ⅰ）由已知得，取的中点T，连接，由N为中点知，.又，故平行且等于，四边形AMNT为平行四边形，于是.因为平面，平面，所以平面.（Ⅱ）因为平面，N为的中点，所以N到平面的距离为.取的中点，连结.由得，.由得到的

距离为，故145252BCMS==△.所以四面体的体积145323NBCMBCMPAVS−==△.【考点】直线与平面间的平行与垂直关系、三棱锥的体积【技巧点拨】（1）证明立体几何中的平行关系，常常是通过线线平行来实现，而线线平行常常利用三角形的中位线、平行四边形与梯形的平行关系来推证；

（2）求三棱锥的体积关键是确定其高，而高的确定关键又找出顶点在底面上的射影位置，当然有时也采取割补法、体积转换法求解．22．（2016·全国·高考真题）如图，已知正三棱锥P-ABC的侧面是直角三角形，PA=6，顶点P在平面ABC内的正投影为点D，D在平面PAB

内的正投影为点E，连结PE并延长交AB于点G.（Ⅰ）证明：G是AB的中点；（Ⅱ）在图中作出点E在平面PAC内的正投影F（说明作法及理由），并求四面体PDEF的体积．【答案】（Ⅰ）见解析；（Ⅱ）作图见解析，体积为43.【详解】试题分析：证明.ABPG⊥由PAPB=可得G

是AB的中点.（Ⅱ）在平面PAB内，过点E作PB的平行线交PA于点F，F即为E在平面PAC内的正投影.根据正三棱锥的侧面是直角三角形且6PA=，可得2,22.==DEPE在等腰直角三角形EFP中，可得2.==EFPF四面体PDEF的体积1

14222.323==V试题解析：（Ⅰ）因为P在平面ABC内的正投影为D，所以.ABPD⊥因为D在平面PAB内的正投影为E，所以.ABDE⊥所以AB⊥平面PED，故.ABPG⊥又由已知可得，PAPB=，从而G是AB的中点.（Ⅱ）

在平面PAB内，过点E作PB的平行线交PA于点F，F即为E在平面PAC内的正投影.理由如下：由已知可得PBPA⊥，PBPC⊥，又//EFPB,所以EFPAEFPC，⊥⊥,因此EF⊥平面PAC，即点F为E在平面PAC内的正投影.

连结CG，因为P在平面ABC内的正投影为D，所以D是正三角形ABC的中心.由（Ⅰ）知，G是AB的中点，所以D在CG上，故2.3=CDCG由题设可得PC⊥平面PAB，DE⊥平面PAB，所以//DPC，因此21,.33==PEPGDEPC由已知，正三棱锥的侧面是直角三角形且6PA=，可得2,

22.==DEPE在等腰直角三角形EFP中，可得2.==EFPF所以四面体PDEF的体积114222.323==V【考点】线面位置关系及几何体体积的计算【名师点睛】文科立体几何解答题主要考查线面位

置关系的证明及几何体体积的计算,空间中线面位置关系的证明主要包括线线、线面、面面三者的平行与垂直关系,其中推理论证的关键是结合空间想象能力进行推理,注意防止步骤不完整或考虑不全致推理片面,该类题目难度不大,以中档题为主.23．（2015·重庆·高考真题）如图，三棱锥P-ABC

中，平面PAC⊥平面ABC，ABC=2，点D、E在线段AC上，且AD=DE=EC=2，PD=PC=4，点F在线段AB上，且EF//BC．(Ⅰ)证明：AB⊥平面PFE.(Ⅱ)若四棱锥P-DFBC的体积为7，

求线段BC的长.【答案】(1)见解析(2)BC=3或BC=33【分析】（Ⅰ）先由已知易得PEAC⊥，再注意平面PAC⊥平面ABC，且交线为AC，由面面垂直的性质可得PE⊥平面ABC，再由线面垂直的性质可得到ABPE⊥，再注意到//EFBC，而BCAB⊥，从而有ABEF⊥

，那么由线面垂的判定定理可得AB⊥平面PFE，（Ⅱ）设BC=x则可用x将四棱锥PDFBC−的体积表示出来，由已知其体积等于7，从而得到关于x的一个一元方程，解此方程，再注意到0x即可得到BC的长．【详解】证明：如题（20）图.由,DEECPDPC==

知，E为等腰PDC中DC边的中点，故PEAC⊥，又平面PAC⊥平面ABC，平面PAC平面ABCAC=，PE平面PAC，PEAC⊥，所以PE⊥平面ABC，从而PEAB⊥.因ABC=,,ABEF2EFBC⊥故.从而AB与平面PFE内两条相交直线PE，EF都垂直，所以AB⊥平面P

FE.（2）解：设BC=x,则在直角ABC中，222AB=AC=36BCx−−.从而211SABBC=3622ABCxx=−由EFBC∥，知23AFAEABAC==，得AEFABC,故224()S39AEFABCS==，即4S9

AEFABCS=.由1AD=2AE,211421SS=SS3622999AFBAFEABCABCxx===−,从而四边形DFBC的面积为22DFBC11SS-=363629ABCADFSxxxx=−−−273618xx=−由

（1）知，PEPE⊥平面ABC，所以PE为四棱锥P-DFBC的高.在直角PEC中，2222PE=PC4223EC−=−=,体积2DFBC117S362373318PDFBCVPExx−==−=,故得42362430xx−+=，解得29x=或227x=由于0x，可得333xx==或.所以

3BC=或33BC=.考点：1.空间线面垂直关系，2.锥体的体积，3.方程思想.24．（2015·全国·高考真题）如图四边形ABCD为菱形，G为AC与BD交点，BEABCD⊥平面，（I）证明：平面AEC⊥平面BED；（II）

若120ABC=，,AEEC⊥三棱锥EACD−的体积为63，求该三棱锥的侧面积.【答案】（1）见解析（2）3+25【分析】（1）由四边形ABCD为菱形知AC⊥BD，由BE⊥平面ABCD知AC⊥BE，由线面垂直判定定理知AC⊥平面BED，由面面垂直的判

定定理知平面AEC⊥平面BED；（2）设AB=x，通过解直角三角形将AG、GC、GB、GD用x表示出来，在RtAEC中，用x表示EG，在RtEBG中，用x表示EB，根据条件三棱锥EACD−的体积为63求出x，即可求出三棱锥EACD−的侧面积.【详解】（1）因为四

边形ABCD为菱形，所以AC⊥BD，因为BE⊥平面ABCD，所以AC⊥BE，故AC⊥平面BED.又AC平面AEC，所以平面AEC⊥平面BED（2）设AB=x，在菱形ABCD中，由ABC=120°，可得

AG=GC=32x,GB=GD=2x.因为AE⊥EC，所以在RtAEC中，可得EG=32x.连接EG，由BE⊥平面ABCD，知EBG为直角三角形，可得BE=22x.由已知得，三棱锥E-ACD的体积3116632243EACDVACGDBEx−===.故x=2从而可得AE=EC=ED=

6.所以EAC的面积为3，EAD的面积与ECD的面积均为5.故三棱锥E-ACD的侧面积为3+25.【点睛】本题考查线面垂直的判定与性质；面面垂直的判定；三棱锥的体积与表面积的计算；逻辑推理能力；运算求解能力.25．（2015·湖南·高考真题）如图，直三棱柱111ABCABC-

的底面是边长为2的正三角形，,EF分别是1,BCCC的中点．（１）证明：平面AEF⊥平面11BBCC；（２）若直线1AC与平面11AABB所成的角为45，求三棱锥FAEC−的体积．【答案】（Ⅰ）见解析；（Ⅱ）612.【详解】试题分

析：（１）由面面垂直的判定定理很容易得结论；（２）所求三棱锥底面积容易求得，是本题转化为求三棱锥的高FC，利用直线1AC与平面11AABB所成的角为，作出线面角，进而可求得的值，则可得的FC长．试题解析：（

1）如图，因为三棱柱111ABCABC-是直三棱柱，所以1⊥，又是正三角形C的边C的中点，所以C⊥又1C=，因此⊥平面11CC而平面F，所以平面F⊥平面11CC（2）设

的中点为D，连结1D,CD因为C是正三角形，所以CD⊥又三棱柱111ABCABC-是直三棱柱，所以1CD⊥因此CD⊥平面11，于是1CD为直线1C与平面11所成的角，由题设，1CD45=，所以13DCD32===在1RtD

中，2211DD312=−=−=，所以112FC22==故三棱锥FC−的体积C11326VFC332212S===考点：直线与平面垂直的判定定理；直线与平面所成的角；几何体的体积．

26．（2015·湖南·高考真题）如图，已知四棱台1111ABCDABCD−的上、下底面分别是边长为3和6的正方形，16AA=，且1AA⊥底面ABCD，点,PQ分别在棱1,DDBC上．（1）若P是1DD的中点，证明：1ABPQ⊥；（2）若//PQ平面11ABBA，二面角

PQDA−−的余弦值为37，求四面体ADPQ的体积．【答案】（1）见解析（2）24V=【详解】根据已知条件知AB，AD，1AA三直线两两垂直，所以分别以这三直线为x，y，z轴，建立如图所示空间直角坐标系，则：(0A，0，0)，(6B，0，0)，(

0D，6，0)，1(0A，0，6)，1(3B，0，6)，1(0D，3，6)；Q在棱BC上，设(6Q，1y，0)，106y剟；（1）证明：若P是1DD的中点，则9(0,,3)2P；19(6,,3)2PQy=−−，1(3,0

,6)AB=；10ABPQ=；1ABPQ⊥；1ABPQ⊥；（2）设(0P，2y，2)z，2y，2[0z，6]，P在棱1DD上；1DPDD=，01剟；(0，26y−，2)(0z=，3−，6)；22636yz

−=−=；22122zy=−；(0P，2y，2122)y−；122(6,,212)PQyyy=−−；平面11ABBA的一个法向量为(0,6,0)AD=；//PQ平面11ABBA；12

6()0PQADyy=−=；12yy=；(6Q，2y，0)；设平面PQD的法向量为(,,)nxyz=，则：226(212)06(6)0nPQxyznDQxyy=+−==+−=；2632

yxzyz−==，取1z=，则26(,2,1)3yn−=；又平面AQD的一个法向量为1(0,0,6)AA=；又二面角PQDA−−的余弦值为37；12263cos,766()53nAAy==−+；解得24y=，或28y=（舍去）；(0P，4，4)；三棱锥PADQ−的

高为4，且166182ADQS==；1184243ADPQPADQVV−===四面体三棱锥．考点：1.空间向量的运用；2.线面垂直的性质；3.空间几何体体积计算.【名师点睛】本题主要考查了线面垂直的性质以及空间几何体体积

计算，属于中档题，由于空间向量工具的引入，使得立体几何问题除了常规的几何法之外，还可以考虑利用向量工具来解决，因此有关立体几何的问题，可以建立空间直角坐标系，借助于向量知识来解决，在立体几何的线面关系中，中点是经常使用的一

个特殊点，无论是试题本身的已知条件，还是在具体的解题中，通过找“中点”，连“中点”，即可出现平行线而线线平行是平行关系的根本，在垂直关系的证明中线线垂直是核心，也可以根据已知的平面图形通过计算的方式证明线线垂直，也可以根据已知的垂直关系证明线线垂直.27．（2015·湖北·高

考真题）《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖臑．在如图所示的阳马PABCD−中，侧棱PD⊥底面ABCD，且PDCD=，点E是PC的中点，连接,,DEBDBE．（Ⅰ）

证明：DE⊥平面PBC．试判断四面体EBCD是否为鳖臑，若是，写出其每个面的直角（只需写出结论）；若不是，请说明理由；（Ⅱ）记阳马PABCD−的体积为1V，四面体EBCD的体积为2V，求12VV的值．【答案】（Ⅰ）因为PD⊥底面ABCD，所以PDBC⊥．由底面ABCD为长方形，有BC

CD⊥，而PDCDD=，所以BC⊥平面PCD．DE平面PCD，所以BCDE⊥．又因为PDCD=，点E是PC的中点，所以DEPC⊥．而PCBCC=，所以DE⊥平面PBC．四面体EBCD是一个鳖臑；（Ⅱ）124.VV=【详解】（Ⅰ）因为PD⊥底面ABCD，所以P

DBC⊥．由底面ABCD为长方形，有BCCD⊥，而PDCDD=，所以BC⊥平面PCD．DE平面PCD，所以BCDE⊥．又因为PDCD=，点E是PC的中点，所以DEPC⊥．而PCBCC=，所以DE⊥平面PBC．由BC⊥平面PCD，DE⊥平面PBC，可知四

面体EBCD的四个面都是直角三角形，即四面体EBCD是一个鳖臑，其四个面的直角分别是,,,.BCDBCEDECDEB（Ⅱ）由已知，PD是阳马PABCD−的高，所以11133ABCDVSPDBCC

DPD==；由（Ⅰ）知，DE是鳖臑DBCE−的高，BCCE⊥，所以21136BCEVSDEBCCEDE==．在Rt△PDC中，因为PDCD=，点E是PC的中点，所以22DECECD==，于是121234.1

6BCCDPDVCDPDVCEDEBCCEDE===考点：本题考查直线与平面垂直的判定定理、直线与平面垂直的性质定理和简单几何体的体积，属中高档题．28．（2015·福建·高考真题）如图，AB是圆O的直径，点

C是圆O上异于,AB的点，垂直于圆所在的平面，且1==．（Ⅰ）若D为线段AC的中点，求证C⊥平面D；（Ⅱ）求三棱锥−PABC体积的最大值；（Ⅲ）若2BC=，点E在线段PB上，求CEOE+的最小值．【答案】（Ⅰ

）详见解析；（Ⅱ）13；（Ⅲ）262+．【详解】（Ⅰ）在C中，因为C=，D为C的中点，所以CD⊥．又垂直于圆所在的平面，所以C⊥．因为D=，所以C⊥平面D．（

Ⅱ）因为点C在圆上，所以当C⊥时，C到的距离最大，且最大值为1．又2=，所以C面积的最大值为12112=．又因为三棱锥C−的高1=，故三棱锥C−体积的最大值为111133=．（Ⅲ）在中，1

==，90=，所以22112=+=．同理C2=，所以CC==．在三棱锥C−中，将侧面C绕旋转至平面C，使之与平面共面，如图所示．当，，C共线时，C+取得最小值．又因为=，CC=，所以C垂直平分，即为

中点．从而2626222CC+=+=+=，亦即C+的最小值为262+．考点：1、直线和平面垂直的判定；2、三棱锥体积．29．（2015·北京·高考真题）如图，在三棱锥VC−中，平面V⊥平面C，V为等边三角形，CC⊥且CC2==，

，分别为，V的中点．(1)求证：V//平面C；(2)求证：平面C⊥平面V；(3)求三棱锥VC−的体积．【答案】（1）见解析；（2）见解析；（3）33.【详解】试题分析：（Ⅰ）利用三角形的中位线得出OM∥

VB，利用线面平行的判定定理证明VB∥平面MOC；（Ⅱ）证明OC⊥平面VAB，即可证明平面MOC⊥平面VAB；（Ⅲ）利用等体积法求三棱锥A-MOC的体积即可试题解析：（Ⅰ）证明：∵O，M分别为AB，VA的中点，∴OM∥VB，∵VB⊄平面MOC，OM⊂平面MO

C，∴VB∥平面MOC；（Ⅱ）证明：∵AC=BC，O为AB的中点，∴OC⊥AB，又∵平面VAB⊥平面ABC，平面ABC∩平面VAB=AB，且OC⊂平面ABC，∴OC⊥平面VAB，∵OC⊂平面MOC，∴平面MOC⊥平

面VAB（Ⅲ）在等腰直角三角形ACB中，2ACBC==，所以2,1ABOC==.所以等边三角形V的面积3VABS=.又因为OC⊥平面V，所以三棱锥CV−的体积等于1333VABOCS

=.又因为三棱锥VC−的体积与三棱锥CV−的体积相等，所以三棱锥VC−的体积为33.考点：平面与平面垂直的判定；直线与平面平行的判定；用向量证明平行考点05异面直线所成角及最值或范围1．（2018·天津·高考真题）如图，在四面体ABCD中，△ABC是等边三角形，平面AB

C⊥平面ABD，点M为棱AB的中点，AB=2，AD=23，∠BAD=90°．（Ⅰ）求证：AD⊥BC；（Ⅱ）求异面直线BC与MD所成角的余弦值；（Ⅲ）求直线CD与平面ABD所成角的正弦值．【答案】(Ⅰ)证明见解析；(Ⅱ)1326；(Ⅲ)34．【详解】分析：（Ⅰ）由面面垂直的性质

定理可得AD⊥平面ABC，则AD⊥BC．（Ⅱ）取棱AC的中点N，连接MN，ND．由几何关系可知∠DMN（或其补角）为异面直线BC与MD所成的角．计算可得113226MNcosDMNDM==．则异面直线BC

与MD所成角的余弦值为1326．（Ⅲ）连接CM．由题意可知CM⊥平面ABD．则∠CDM为直线CD与平面ABD所成的角．计算可得34CMsinCDMCD==．即直线CD与平面ABD所成角的正弦值为34．详解：（Ⅰ

）证明：由平面ABC⊥平面ABD，平面ABC∩平面ABD=AB，AD⊥AB，可得AD⊥平面ABC，故AD⊥BC．（Ⅱ）取棱AC的中点N，连接MN，ND．又因为M为棱AB的中点，故MN∥BC．所以∠DMN（或其补角）为异面直线BC与MD所成的角．在Rt

△DAM中，AM=1，故DM=22=13ADAM+．因为AD⊥平面ABC，故AD⊥AC．在Rt△DAN中，AN=1，故DN=22=13ADAN+．在等腰三角形DMN中，MN=1，可得1132cos26MNDMNDM==．所以，

异面直线BC与MD所成角的余弦值为1326．（Ⅲ）连接CM．因为△ABC为等边三角形，M为边AB的中点，故CM⊥AB，CM=3．又因为平面ABC⊥平面ABD，而CM平面ABC，故CM⊥平面ABD．所以，∠CDM为直线CD与平面ABD所成的角．在Rt△CAD中，CD=22ACAD+=4

．在Rt△CMD中，3sin4CMCDMCD==．所以，直线CD与平面ABD所成角的正弦值为34．点睛：本小题主要考查异面直线所成的角、直线与平面所成的角、平面与平面垂直等基础知识．考查空间想象能力、运算求解能力和推理

论证能力．2．（2017·天津·高考真题）如图，在四棱锥PABCD−中，AD⊥平面PDC，ADBC，PDPB⊥，1AD=，3BC=，4CD=，2PD=.（I）求异面直线AP与BC所成角的余弦值；（II）求证：PD⊥平面PBC；（Ⅲ）求直线AB与平面PBC所成角的正弦值.【答

案】（Ⅰ）55.（Ⅱ）见解析;（Ⅲ）55.【分析】（Ⅰ）由已知AD//BC，故DAP或其补角即为异面直线AP与BC所成的角，然后在Rt△PDA中求解即可；（Ⅱ）因为AD⊥平面PDC，所以AD⊥PD，PD⊥BC，又PD⊥PB，所以PD⊥平面PBC；（Ⅲ）过点D作AB的

平行线交BC于点F，连结PF，则DF与平面PBC所成的角等于AB与平面PBC所成的角，且DFP为直线DF和平面PBC所成的角，然后在Rt△DPF中求解即可.【详解】解：（Ⅰ）如图，由已知AD//BC，故DAP或其补角即为异面直线AP与BC所成的角.

因为AD⊥平面PDC，所以AD⊥PD.在Rt△PDA中，由已知，得225APADPD=+=，故5cos5ADDAPAP==.所以，异面直线AP与BC所成角的余弦值为55.（Ⅱ）证明：因为AD⊥平面PDC，直线PD平面PDC，所以A

D⊥PD.又因为BC//AD，所以PD⊥BC，又PD⊥PB，BCPBB=所以PD⊥平面PBC.（Ⅲ）过点D作AB的平行线交BC于点F，连结PF，则DF与平面PBC所成的角等于AB与平面PBC所成的角.因为PD⊥平面PBC，故PF为DF在平面PBC上的射影，所以DFP为直线DF和平面P

BC所成的角.由于AD//BC，DF//AB，故BF=AD=1，由已知，得CF=BC–BF=2.又AD⊥DC，故BC⊥DC，在Rt△DCF中，可得2225DFCDCF=+=,在Rt△DPF中，可得5sin5PDDFPDF==.所以，直线AB与平面PBC所成角的正弦值为55.考点：两条

异面直线所成的角、直线与平面垂直、直线与平面所成的角【点睛】本小题主要考查两条异面直线所成的角、直线与平面垂直的证明、直线与平面所成的角，要求一定的空间想象能力、运算求解能力和推理论证能力.求两条异面直线所成的角，首先要借助平行线找出异面直线所成的角，证明线面垂直只需寻求线线垂直，求

线面角首先利用转化思想寻求直线与平面所成的角，然后再计算即可.3．（2016·上海·高考真题）将边长为1的正方形11AAOO（及其内部）绕1OO旋转一周形成圆柱，如图，AC长为23，11AB长为3，其中1B与C在平面11AAOO的同侧.(

1)求三棱锥111COAB−的体积；(2)求异面直线1BC与1AA所成的角的大小.【答案】(1)312(2)4.【详解】试题分析：（1）由题意可知，圆柱的高1h=，底面半径1r=，1113=，再由三角形面积公式计算111

S后即得.（2）设过点1的母线与下底面交于点，根据11//，知1CΒΒ或其补角为直线1ΒC与1所成的角，再结合题设条件确定π3CΟΒ=，1CΒ=．得出1π4CΒΒ=即可．试题解析：（1）由题意可知，圆柱的高1h=，底面半径1r=．由11AB的长为π3，可知1113

=．111111111113sin24ΟΑΒSΟΑΟΒAΟΒ==△，11111113V312COABSh−==．（2）设过点1的母线与下底面交于点，则11//，所以1CΒΒ或其补角为直线1ΒC与1所成的角．由AC长为

2π3，可知2π3ΑΟC=，又111π3ΑΟΒΑΟΒ==，所以π3CΟΒ=，从而CΟΒ△为等边三角形，得1CΒ=．因为1⊥平面ΑΟC，所以1ΒΒCΒ⊥．在1CΒΒ△中，因为1π2ΒΒC=，1CΒ

=，11=，所以1π4CΒΒ=，从而直线1ΒC与1所成的角的大小为π4．【考点】几何体的体积、空间角【名师点睛】此类题目是立体几何中的常见问题.解答本题时，关键在于能利用直线与直线、直线与平面、平面与平面位置关系的相互转化，将空间问题转化成平面问题.立体几

何中的角与距离的计算问题，往往可以利用几何法、空间向量方法求解，应根据题目条件，灵活选择方法.本题能较好地考查考生的空间想象能力、逻辑推理能力、转化与化归思想及基本运算能力等.4．（2015·广东·高考真题）如图，三角形△PDC所在的平面与长方形

ABCD所在的平面垂直，PD＝PC＝4，AB＝6，BC＝3，点E是CD的中点，点F、G分别在线段AB、BC上，且AF＝2FB，CG＝2GB．（1）证明：PE⊥FG；（2）求二面角P﹣AD﹣C的正切值；（3）求直线PA与直线FG所成角的余弦值．【答案】（1）见解析；（2）73；（3）9525．【

分析】（1）通过△PDC为等腰三角形可得PE⊥CD，利用线面垂直判定定理及性质定理即得结论；（2）通过（1）及面面垂直定理可得PG⊥AD，则∠PDC为二面角P﹣AD﹣C的平面角，利用勾股定理即得结论；（3）连结AC，利用勾股定理及已知条件可得FG∥AC，在△PAC中，利用余弦定理即得直线PA与

直线FG所成角的余弦值．【详解】（1）证明：在△PDC中PO＝PC且E为CD中点，∴PE⊥CD，又∵平面PDC⊥平面ABCD，平面PDC∩平面ABCD＝CD，PE⊂平面PCD，∴PE⊥平面ABCD，又∵FG⊂平面ABCD，∴PE⊥FG；（2）解：由（1）知PE⊥平面ABCD，∴

PE⊥AD，又∵CD⊥AD且PE∩CD＝E，∴AD⊥平面PDC，又∵PD⊂平面PDC，∴AD⊥PD，又∵AD⊥CD，∴∠PDC为二面角P﹣AD﹣C的平面角，在Rt△PDE中，由勾股定理可得：PE2222437PDDE=−=−=，∴tan∠PDC73PGDG==；（3）解：连结AC，则AC226

3=+=35，在Rt△ADP中，AP222234ADDP=+=+=5，∵AF＝2FB，CG＝2GB，∴FG∥AC，∴直线PA与直线FG所成角即为直线PA与直线AC所成角∠PAC，在△PAC中，由余弦定理得cos∠PAC2222PAACPCPAAC+−=2225(35)42535+−=95

25=．【点睛】本题考查线线垂直的判定、二面角及线线角的三角函数值，涉及到勾股定理、余弦定理等知识，注意解题方法的积累，属于中档题．5．（2015·全国·高考真题）（2015新课标全国Ⅰ理科）如图，四边形ABCD为菱形，∠ABC=

120°，E，F是平面ABCD同一侧的两点，BE⊥平面ABCD，DF⊥平面ABCD，BE=2DF，AE⊥EC．（1）证明：平面AEC⊥平面AFC；（2）求直线AE与直线CF所成角的余弦值．【答案】（1）见解析；（2）33.【详解】试题分析：（Ⅰ）连接BD，设BD∩AC=G，连接EG，

FG，EF，在菱形ABCD中，不妨设GB=1易证EG⊥AC，通过计算可证EG⊥FG，根据线面垂直判定定理可知EG⊥平面AFC，由面面垂直判定定理知平面AFC⊥平面AEC；（Ⅱ）以G为坐标原点，分别以,GBGC的方向为x轴，y轴正方向，||GB为单位长度，建立空间直角坐标系G-

xyz，利用向量法可求出异面直线AE与CF所成角的余弦值.试题解析：（Ⅰ）连接BD，设BD∩AC=G，连接EG，FG，EF，在菱形ABCD中，不妨设GB=1，由∠ABC=120°，可得AG=GC=3.由BE⊥平面ABCD，AB=BC可知，AE=EC

，又∵AE⊥EC，∴EG=3，EG⊥AC，在Rt△EBG中，可得BE=2，故DF=22.在Rt△FDG中，可得FG=62.在直角梯形BDFE中，由BD=2，BE=2，DF=22可得EF=322，∴222EGFG

EF+=，∴EG⊥FG，∵AC∩FG=G，∴EG⊥平面AFC，∵EG面AEC，∴平面AFC⊥平面AEC.（Ⅱ）如图，以G为坐标原点，分别以,GBGC的方向为x轴，y轴正方向，||GB为单位长度，建立空间直角坐标系G-xyz，由（Ⅰ）可得A（0，－3，0），E（1,0,

2），F（－1,0，22），C（0，3，0），∴AE=（1，3，2），CF=（-1，-3，22）.…10分故3cos,3AECFAECFAECF==−.所以直线AE与CF所成的角的余弦值为33.考点：空间垂直判定与性质；异面直线所成角的计算；空间想象能力，推理论证能力6．（2015·上海·高考真

题）如图，圆锥的顶点为，底面的一条直径为，为半圆弧的中点，为劣弧的中点.已知，，求三棱锥的体积，并求异面直线与所成角的大小.【答案】【详解】因为，，所以三棱锥的体积．因为，所以异面直线与所成的角就是与的夹角.在中，，，过作，则，在中，，所以异面直线与所成角的大小.

考点：圆锥的性质，异面直线的夹角.7．（2015·山东·高考真题）如下图，在四棱锥SABCD−中，底面ABCD是正方形，平面SAD⊥平面ABCD，2SASD==，3AB=．（1）求SA与BC所成角的余弦值；（2）求证：ABSD⊥．【答案】（1）34；（2）证明见解析．【分析】(1)由题意可得S

AD即为SA与BC所成的角，根据余弦定理计算即可；(2)结合面面垂直的性质和线面垂直的性质即可证明.【详解】【考查内容】异面直线所成的角，直线与平面垂直的判定和性质【解】（1）因为//ADBC，因此SAD即为SA与B

C所成的角，在SAD中，2SASD==，又在正方形ABCD中3ADAB==，因此2222222323cos22234SAADSDSADSAAD+−+−===，因此SA与BC所成角的余弦值是34．（2）因为平面SAD⊥平面ABCD，平面S

AD平面ABCDAD=，在正方形ABCD中，ABAD⊥，因此AB⊥平面SAD，又因为SD平面SAD，因此ABSD⊥．考点06求线面角及最值或范围1．（2024·天津·高考真题）已知四棱柱1111ABCDABCD−中，底面ABCD为梯形，//ABCD，1AA⊥

平面ABCD，ADAB⊥，其中12,1ABAAADDC====．N是11BC的中点，M是1DD的中点．(1)求证1//DN平面1CBM；(2)求平面1CBM与平面11BBCC的夹角余弦值；(3)求点B到平面1CBM的距离．【答案】(1)

证明见解析(2)22211(3)21111【分析】（1）取1CB中点P，连接NP，MP，借助中位线的性质与平行四边形性质定理可得1N//DMP，结合线面平行判定定理即可得证；（2）建立适当空间直角坐标系，计算两平面的空间向

量，再利用空间向量夹角公式计算即可得解；（3）借助空间中点到平面的距离公式计算即可得解.【详解】（1）取1CB中点P，连接NP，MP，由N是11BC的中点，故1//NPCC，且112NPCC=，由M是1DD的中点，故1111122DMDDCC==，且11//DMCC，则有1//DMNP、1DM

NP=，故四边形1DMPN是平行四边形，故1//DNMP，又MP平面1CBM，1DN平面1CBM，故1//DN平面1CBM；（2）以A为原点建立如图所示空间直角坐标系，有()0,0,0A、()2,0,0B、()12,0,2B、()0,1,1M、()1,1,0C、()11,1,2C，则

有()11,1,2CB=−、()1,0,1CM=−、()10,0,2BB=，设平面1CBM与平面11BBCC的法向量分别为()111,,mxyz=、()222,,nxyz=，则有111111200mCBxyzmCMxz=−+==−+=，1222122020nCBxyzn

BBz=−+===，分别取121xx==，则有13y=、11z=、21y=，20z=，即()1,3,1m=、()1,1,0n=，则13222cos,1119111mnmnmn+===+++，故平面1

CBM与平面11BBCC的夹角余弦值为22211；（3）由()10,0,2BB=，平面1CBM的法向量为()1,3,1m=，则有1221111191BBmm==++，即点B到平面1CBM的距离为21111.2．（2024·上海·高考真题）如图为正四棱锥,PABCDO−为底面

ABCD的中心．(1)若5,32APAD==，求POA绕PO旋转一周形成的几何体的体积；(2)若,APADE=为PB的中点，求直线BD与平面AEC所成角的大小．【答案】(1)12π(2)π4【分析】（1）根据正四棱锥的数据，先算出

直角三角形POA的边长，然后求圆锥的体积；（2）连接,,EAEOEC，可先证BE⊥平面ACE，根据线面角的定义得出所求角为BOE，然后结合题目数量关系求解.【详解】（1）正四棱锥满足且PO⊥平面ABCD，由AO平面ABCD，则POA

O⊥，又正四棱锥底面ABCD是正方形，由32=AD可得，3AO=，故224POPAAO=−=，根据圆锥的定义，POA绕PO旋转一周形成的几何体是以PO为轴，AO为底面半径的圆锥，即圆锥的高为4PO=，底面半径为3AO=，根据圆锥的体积公式，所得圆锥的体积是21π3412π3=（2

）连接,,EAEOEC，由题意结合正四棱锥的性质可知，每个侧面都是等边三角形，由E是PB中点，则,AEPBCEPB⊥⊥，又,,AECEEAECE=平面ACE，故PB⊥平面ACE，即BE⊥平面ACE，又BD平面AC

EO=，于是直线BD与平面AEC所成角的大小即为BOE，不妨设6APAD==，则32,3BOBE==，32sin232BOE==，又线面角的范围是π0,2，故π4BOE=.即为所求.3．（2023·全国甲卷·高考真题）如图，在三棱柱111ABCABC-中，1AC⊥

底面ABC，190,2ACBAA==，1A到平面11BCCB的距离为1．(1)证明：1ACAC=；(2)已知1AA与1BB的距离为2，求1AB与平面11BCCB所成角的正弦值．【答案】(1)证明见解析(2)1313【分析】（1）根据

线面垂直，面面垂直的判定与性质定理可得1AO⊥平面11BCCB，再由勾股定理求出O为中点，即可得证；（2）利用直角三角形求出1AB的长及点A到面的距离，根据线面角定义直接可得正弦值.【详解】（1）如图，1AC⊥底面ABC，B

C面ABC，1ACBC⊥，又BCAC⊥，1,ACAC平面11ACCA，1ACACC=,BC⊥平面ACC1A1，又BC平面11BCCB，平面11ACCA⊥平面11BCCB，过1A作11AOCC⊥交1CC于O，又平面11ACC

A平面111BCCBCC=，1AO平面11ACCA，1AO⊥平面11BCCB1A到平面11BCCB的距离为1，11=AO，在11RtACC△中，111112,ACACCCAA⊥==，设COx=，则12COx=−，11

111,,AOCAOCACC△△△为直角三角形，且12CC=，22211COAOAC+=，2221111AOOCCA+=，2221111ACACCC+=，2211(2)4xx+++−=，解得1x=，1112ACACAC==

=，1ACAC=（2）111,,ACACBCACBCAC=⊥⊥，1RtRtACBACB△≌△1BABA=，过B作1BDAA⊥，交1AA于D，则D为1AA中点，由直线1AA与1BB距离为2，所以2B

D=11AD=，2BD=，15ABAB==，在RtABC△，223BCABAC=−=，延长AC，使ACCM=，连接1CM，由1111,CMACCMAC=∥知四边形11ACMC为平行四边形，11CMAC∥，1CM⊥平面ABC，又AM平面ABC，1CMAM⊥则在1RtACM△中，112,

AMACCMAC==，2211(2)ACACAC=+，在11RtABC△中，2211(2)ACACAC=+，113BCBC==，2221(22)(2)(3)13AB=++=,又A到平面11BCCB距离也为1，所

以1AB与平面11BCCB所成角的正弦值为1131313=.4．（2022·全国甲卷·高考真题）在四棱锥PABCD−中，PD⊥底面,,1,2,3ABCDCDABADDCCBABDP=====∥．(1)证明：BDPA⊥；(2)求PD与平面PAB所成的角的正弦值．【答案】(1)证明见解析；(2

)55.【分析】（1）作DEAB⊥于E，CFAB⊥于F，利用勾股定理证明ADBD⊥，根据线面垂直的性质可得PDBD⊥，从而可得BD⊥平面PAD，再根据线面垂直的性质即可得证；（2）以点D为原点建立空间直角坐标系，利用向量法即可得出答案.【详解】（1）证明：在四边形A

BCD中，作DEAB⊥于E，CFAB⊥于F，因为//,1,2CDABADCDCBAB====，所以四边形ABCD为等腰梯形，所以12AEBF==，故32DE=，223BDDEBE=+=，所以222ADBDAB+=，所以ADBD⊥，因为PD⊥平面ABCD，BD平面

ABCD，所以PDBD⊥，又=PDADD，所以BD⊥平面PAD，又因为PA平面PAD，所以BDPA⊥；（2）解：如图，以点D为原点建立空间直角坐标系，3BD=，则()()()1,0,0,0,3,0,0,0,3ABP，则()()()1,0,3,0,3,3,0,0,3APBPDP=−=−=

，设平面PAB的法向量(),,nxyz=，则有30{330nAPxznBPyz=−+==−+=，可取()3,1,1n=，则5cos,5nDPnDPnDP==，所以PD与平面PAB所成角的正弦值为55.5．（2022·全国乙卷·高考真题）如图，四面体ABCD中，,,ADC

DADCDADBBDC⊥==，E为AC的中点．(1)证明：平面BED⊥平面ACD；(2)设2,60ABBDACB===，点F在BD上，当AFC△的面积最小时，求CF与平面ABD所成的角的正弦值．【答案】(1)证明过程见解析(2)CF与平面AB

D所成的角的正弦值为437【分析】（1）根据已知关系证明ABDCBD≌△△，得到ABCB=，结合等腰三角形三线合一得到垂直关系，结合面面垂直的判定定理即可证明；（2）根据勾股定理逆用得到BEDE⊥，从而建立空间直角坐

标系，结合线面角的运算法则进行计算即可.【详解】（1）因为ADCD=，E为AC的中点，所以ACDE⊥；在ABD△和CBD△中，因为,,BACDCDADBDBDBD===，所以ABDCBD≌△△，所以ABCB=，又因为E为AC的中点，所以A

CBE⊥；又因为,DEBE平面BED，DEBEE=，所以AC⊥平面BED，因为AC平面ACD，所以平面BED⊥平面ACD.（2）连接EF，由（1）知，AC⊥平面BED，因为EF平面BED，所以ACEF⊥，所以1=2AFCSACEF△，当EFBD⊥时，E

F最小，即AFC△的面积最小.因为ABDCBD≌△△，所以2CBAB==，又因为60ACB=，所以ABC是等边三角形，因为E为AC的中点，所以1AEEC==，3BE=，因为ADCD⊥，所以112DEAC==,在DEB中，222DEBEBD+=，所以BEDE⊥.以E为坐标原点建立如

图所示的空间直角坐标系Exyz−，则()()()1,0,0,0,3,0,0,0,1ABD，所以()()1,0,1,1,3,0ADAB=−=−，设平面ABD的一个法向量为(),,nxyz=，则030nADxznA

Bxy=−+==−+=，取3y=，则()3,3,3n=，又因为()331,0,0,0,,44CF−，所以331,,44CF=，所以643cos,77214nCFnCFnCF===，设CF与平面ABD

所成的角为02，所以43sincos,7nCF==，所以CF与平面ABD所成的角的正弦值为437.6．（2022·浙江·高考真题）如图，已知ABCD和CDEF都是直角梯形，//ABD

C，//DCEF，5AB=，3DC=，1EF=，60BADCDE==，二面角FDCB−−的平面角为60．设M，N分别为,AEBC的中点．(1)证明：FNAD⊥；(2)求直线BM与平面ADE所成角的正弦值．【答案】(1)证明见解析；(2)5714．【分析】（1）过点E

、D分别做直线DC、AB的垂线EG、DH并分别交于点G、H，由平面知识易得FCBC=，再根据二面角的定义可知，60BCF=，由此可知，FNBC⊥，FNCD⊥，从而可证得FN⊥平面ABCD，即得FNAD⊥；（2）由（1）可知FN⊥平面ABCD，过点N做AB平行线NK，所以可以以点N

为原点，NK，NB、NF所在直线分别为x轴、y轴、z轴建立空间直角坐标系Nxyz−，求出平面ADE的一个法向量，以及BM，即可利用线面角的向量公式解出．【详解】（1）过点E、D分别做直线DC、AB的垂线EG、DH并分别交于点G、H．∵四边形ABCD和EFCD都

是直角梯形，//,//,5,3,1ABDCCDEFABDCEF===，60BADCDE==，由平面几何知识易知，2,90DGAHEFCDCFDCBABC======，则四边形EFCG和四边形DCBH

是矩形，∴在RtEGD和RtDHA，23EGDH==，∵,DCCFDCCB⊥⊥，且CFCBC=，∴DC⊥平面,BCFBCF是二面角FDCB−−的平面角，则60BCF=，∴BCF△是正三角形，由DC平面ABCD，得平面ABCD⊥平面BCF，∵N是BC的中点，FNBC⊥，又DC⊥平面

BCF，FN平面BCF，可得FNCD⊥，而BCCDC=，∴FN⊥平面ABCD，而AD平面ABCDFNAD⊥．（2）因为FN⊥平面ABCD，过点N做AB平行线NK，所以以点N为原点，NK，NB、NF所在直线

分别为x轴、y轴、z轴建立空间直角坐标系Nxyz−，设(5,3,0),(0,3,0),(3,3,0),(1,0,3)ABDE−，则333,,22M，333,,,(2,23,0),(2,3,3)22BMADDE=−=−−=−设平面ADE的法向量为(

,,)nxyz=由00nADnDE==，得22302330xyxyz−−=−++=，取(3,1,3)n=−，设直线BM与平面ADE所成角为，∴3333322||5357sincos,14|||39723313944nBMnBMnBM++=====++++．7

．（2022·天津·高考真题）直三棱柱111ABCABC-中，112,,AAABACAAABACAB===⊥⊥，D为11AB的中点，E为1AA的中点，F为CD的中点．(1)求证：//EF平面ABC；(2)求直线BE与平面1CCD所成角的正弦值；(3)求平面1ACD与平面

1CCD夹角的余弦值．【答案】(1)证明见解析(2)45(3)1010【分析】（1）以点1A为坐标原点，1AA、11AB、11AC所在直线分别为x、y、z轴建立空间直角坐标系，利用空间向量法可证得结论成立；（2）利用空间向量法

可求得直线BE与平面1CCD夹角的正弦值；（3）利用空间向量法可求得平面1ACD与平面1CCD夹角的余弦值.【详解】（1）证明：在直三棱柱111ABCABC-中，1AA⊥平面111ABC，且ACAB⊥，则1111ACAB⊥以点1A为坐标原点，1AA、11AB、11AC所在直线分别为x、y

、z轴建立如下图所示的空间直角坐标系，则()2,0,0A、()2,2,0B、()2,0,2C、()10,0,0A、()10,2,0B、()10,0,2C、()0,1,0D、()1,0,0E、11,,12F，则10,,12EF=，易知平面ABC的一个法

向量为()1,0,0m=，则0EFm=，故EFm⊥，EF平面ABC，故//EF平面ABC.（2）解：()12,0,0CC=，()10,1,2CD=−，()1,2,0EB=，设平面1CCD的法向量为()111,,uxyz=，则111112020uCCxuCDyz===−=

，取12y=，可得()0,2,1u=，4cos,5EBuEBuEBu==.因此，直线BE与平面1CCD夹角的正弦值为45.（3）解：()12,0,2AC=，()10,1,0AD=，设平面1ACD的法向量为

()222,,vxyz=，则122122200vACxzvADy=+===，取21x=，可得()1,0,1v=−，则110cos,1052uvuvuv==−=−，因此，平面1ACD与平面1CCD夹角的余弦值为1010.8．（2021·浙江·

高考真题）如图，在四棱锥PABCD−中，底面ABCD是平行四边形，120,1,4,15ABCABBCPA====，M，N分别为,BCPC的中点，,PDDCPMMD⊥⊥.（1）证明：ABPM⊥；（2）求直线AN与平面PDM

所成角的正弦值.【答案】（1）证明见解析；（2）156．【分析】（1）要证ABPM⊥，可证DCPM⊥，由题意可得，PDDC⊥，易证DMDC⊥，从而DC⊥平面PDM，即有DCPM⊥，从而得证；（2）取AD中点E，根据题意可知，,,MEDMPM两两垂直，所以

以点M为坐标原点，建立空间直角坐标系，再分别求出向量AN和平面PDM的一个法向量，即可根据线面角的向量公式求出．【详解】（1）在DCM△中，1DC=，2CM=，60DCM=，由余弦定理可得3DM=，所以222DMDCCM

+=，DMDC⊥．由题意DCPD⊥且PDDMD=，DC⊥平面PDM，而PM平面PDM，所以DCPM⊥，又//ABDC，所以ABPM⊥．（2）由PMMD⊥，ABPM⊥，而AB与DM相交，所以PM⊥平面ABCD，因为7AM=，所以22PM=，取AD中点E，连接ME，则,

,MEDMPM两两垂直，以点M为坐标原点，如图所示，建立空间直角坐标系,则(3,2,0),(0,0,22),(3,0,0)APD−,(0,0,0),(3,1,0)MC−又N为PC中点，所以31335,,2,,,22222NAN−=−.由（1）得C

D⊥平面PDM，所以平面PDM的一个法向量(0,1,0)n=从而直线AN与平面PDM所成角的正弦值为5||152sin6||2725244ANnANn===++‖．【点睛】本题第一问主要考查线面垂直的相互转化，要证明ABPM⊥，可以考虑DCPM⊥，题中与DC有垂直关系的直线较

多，易证DC⊥平面PDM，从而使问题得以解决；第二问思路直接，由第一问的垂直关系可以建立空间直角坐标系，根据线面角的向量公式即可计算得出．9．（2020·海南·高考真题）如图，四棱锥P-ABCD的底面为正方形，PD⊥底面ABCD

．设平面PAD与平面PBC的交线为l．（1）证明：l⊥平面PDC；（2）已知PD=AD=1，Q为l上的点，QB=2，求PB与平面QCD所成角的正弦值．【答案】（1）证明见解析；（2）63.【分析】（1）利用线面平行的判定定理以及性质定理，证得//ADl，利用线面垂直的判定定

理证得AD⊥平面PDC，从而得到l⊥平面PDC；（2）根据题意，建立相应的空间直角坐标系，得到相应点的坐标，设出点(,0,1)Qm，之后求得平面QCD的法向量以及向量PB的坐标，求得cos,nPB，即可得到直线PB与平面QCD所成角的正弦值.【详解】（1）证明：在

正方形ABCD中，//ADBC，因为AD平面PBC，BC平面PBC，所以//AD平面PBC，又因为AD平面PAD，平面PAD平面PBCl=，所以//ADl，因为在四棱锥PABCD−中，底面ABCD是正方形，所以,,ADDClDC

⊥⊥且PD⊥平面ABCD，所以,,ADPDlPD⊥⊥因为CDPDD=所以l⊥平面PDC；（2）如图建立空间直角坐标系Dxyz−，因为1PDAD==，则有(0,0,0),(0,1,0),(1,0,0),(0,0,1),(1,1,0)DCAPB，设(,0

,1)Qm，则有(0,1,0),(,0,1),(1,1,1)DCDQmPB===−，因为QB=2，所以有222(1)(01)(10)21mm−+−+−==设平面QCD的法向量为(,,)nxyz=，则00DCnDQn

==，即00yxz=+=，令1x=，则1z=−，所以平面QCD的一个法向量为(1,0,1)n=−，则22222210126cos,.32310(1)111nPBnPBnPB++====++−++根据直线的方向向量与平面法向量所成角的余弦值的绝对值

即为直线与平面所成角的正弦值，所以直线与平面所成角的正弦值等于6|cos,|3nPB=ruur所以直线PB与平面QCD所成角的正弦值为63.【点睛】该题考查的是有关立体几何的问题，涉及到的知识点有线面平行的判定和性质，线面垂直的判定和性质，利用空间向量求

线面角，利用基本不等式求最值，属于中档题目.10．（2020·天津·高考真题）如图，在三棱柱111ABCABC-中，1CC⊥平面,,2ABCACBCACBC⊥==，13CC=，点,DE分别在棱1AA和棱1CC上，且12,ADCEM==为棱11AB的中点．（Ⅰ）求

证：11CMBD⊥；（Ⅱ）求二面角1BBED−−的正弦值；（Ⅲ）求直线AB与平面1DBE所成角的正弦值．【答案】（Ⅰ）证明见解析；（Ⅱ）306；（Ⅲ）33.【分析】以C为原点，分别以1,,CACBCC的方向为x轴，y轴，z轴的正方向建立空间直角坐标系.

（Ⅰ）计算出向量1CM和1BD的坐标，得出110CMBD=，即可证明出11CMBD⊥；（Ⅱ）可知平面1BBE的一个法向量为CA，计算出平面1BED的一个法向量为n，利用空间向量法计算出二面角1BBED−

−的余弦值，利用同角三角函数的基本关系可求解结果；（Ⅲ）利用空间向量法可求得直线AB与平面1DBE所成角的正弦值.【详解】依题意，以C为原点，分别以CA、CB、1CC的方向为x轴、y轴、z轴的正方向建立空间直角坐标系（如图），可

得()0,0,0C、()2,0,0A、()0,2,0B、()10,0,3C、()12,0,3A、()10,2,3B、()2,0,1D、()0,0,2E、()1,1,3M.（Ⅰ）依题意，()11,1,0CM=，()12,2,2BD=−−，从而112200CMBD=−+=，所以11CMBD

⊥；（Ⅱ）依题意，()2,0,0CA=是平面1BBE的一个法向量，()10,2,1EB=，()2,0,1ED=−．设(),,nxyz=为平面1DBE的法向量，则100nEBnED==，即2020yzxz+=−=

，不妨设1x=，可得()1,1,2n=−．26cos,626CCAnACnAn===，230sin,1cos,6CAnCAn=−=．所以，二面角1BBED−−的正弦值为306；（Ⅲ）依题意，()2,2,0AB=−．由（Ⅱ）知()1

,1,2n=−为平面1DBE的一个法向量，于是43cos,3226ABnABnABn−===−．所以，直线AB与平面1DBE所成角的正弦值为33.【点睛】本题考查利用空间向量法证明线线垂直，求二面角和线面角的正弦值，考查推理能力与计算能力，属于中档题.11．（2020·北

京·高考真题）如图，在正方体1111ABCDABCD−中，E为1BB的中点．（Ⅰ）求证：1//BC平面1ADE；（Ⅱ）求直线1AA与平面1ADE所成角的正弦值．【答案】（Ⅰ）证明见解析；（Ⅱ）23.【分析】（Ⅰ）证明

出四边形11ABCD为平行四边形，可得出11//BCAD，然后利用线面平行的判定定理可证得结论；也可利用空间向量计算证明；（Ⅱ）可以将平面扩展，将线面角转化，利用几何方法作出线面角，然后计算；也可以建立空间直角坐标

系，利用空间向量计算求解.【详解】（Ⅰ）[方法一]：几何法如下图所示：在正方体1111ABCDABCD−中，11//ABAB且11ABAB=，1111//ABCD且1111ABCD=，11//ABCD

且11ABCD=，所以，四边形11ABCD为平行四边形，则11//BCAD，1BC平面1ADE，1AD平面1ADE，1//BC平面1ADE；[方法二]:空间向量坐标法以点A为坐标原点，AD、AB、1AA所在直线分

别为x、y、z轴建立如下图所示的空间直角坐标系Axyz−，设正方体1111ABCDABCD−的棱长为2，则()0,0,0A、()10,0,2A、()12,0,2D、()0,2,1E，()12,0,2AD=，()0,2,1AE=

，设平面1ADE的法向量为(),,nxyz=，由100nADnAE==，得22020xzyz+=+=，令2z=−，则2x=，1y=，则()2,1,2n=−.又∵向量()12,0,2B

C=,()1·2201220BCn=++−=,又1BC平面1ADE，1//BC平面1ADE；（Ⅱ）[方法一]：几何法延长1CC到F，使得1CFBE=，连接EF，交11BC于G，又∵1//CFBE，∴四边形1BEFC为平行四边形，∴1//BCEF，又∵11//BCAD,∴1/

/ADEF,所以平面1ADE即平面1ADFE,连接1DG，作11CHDG⊥,垂足为H,连接FH,∵1FC⊥平面1111DCBA,1DG平面1111DCBA,∴11FCDG⊥，又∵111FCCHC=,∴直线1DG⊥平面1CFH,又∵直线1DG平面1DGF,∴平面1DGF⊥平面1CFH,∴

1C在平面1DGF中的射影在直线FH上,∴直线FH为直线1FC在平面1DGF中的射影，∠1CFH为直线1FC与平面1DGF所成的角，根据直线1//FC直线1AA，可知∠1CFH为直线1AA与平面1ADG所成的角.设正方体的棱长为2，则111CGCF==,15DG=,∴12

1255CH==,∴223155FH=+=,∴112sin3CHCFHFH==,即直线1AA与平面1ADE所成角的正弦值为23.[方法二]：向量法接续（I)的向量方法，求得平面平面1ADE的法向量()2,1,2n=−，又∵()10,0,

2AA=,∴11142cos,323nAAnAAnAA==−=−，∴直线1AA与平面1ADE所成角的正弦值为23.[方法三]：几何法+体积法如图，设11BC的中点为F，延长111,,ABAEDF，易证三线交于一点P．因为111,BBAAEFAD∥∥，所以直线1AA

与平面1ADE所成的角，即直线1BE与平面PEF所成的角．设正方体的棱长为2，在PEF!中，易得5,2PEPFEF===，可得32PEFS=．由11BPEFPBEFVV−−=三棱锥三棱锥，得113111123232BH=，整

理得123BH=．所以1112sin3BHBEHBE==．所以直线1AA与平面1ADE所成角的正弦值为23．[方法四]：纯体积法设正方体的棱长为2，点1A到平面1AED的距离为h，在1AED△中，115,22,3AEADDE===，22211119585cos25235DEAEADAEDDE

AE+−+−===，所以125sin5AED=，易得13AEDS=．由1111EAADAAEDVV−−=，得111111133ADAAEDSABSh=，解得43h=，设直线1AA与平面1AED所成

的角为，所以12sin3hAA==．【整体点评】（Ⅰ）的方法一使用线面平行的判定定理证明，方法二使用空间向量坐标运算进行证明；（II）第一种方法中使用纯几何方法，适合于没有学习空间向量之前的方法，有利用培养学生的集合论证和空间想象能力，第二种方法使用空间向量方法，两小题前后连贯，利用计算

论证和求解，定为最优解法；方法三在几何法的基础上综合使用体积方法，计算较为简洁；方法四不作任何辅助线，仅利用正余弦定理和体积公式进行计算，省却了辅助线和几何的论证，不失为一种优美的方法.12．（2020·浙江·高考真题）如

图，三棱台ABC—DEF中，平面ACFD⊥平面ABC，∠ACB=∠ACD=45°，DC=2BC．（I）证明：EF⊥DB；（II）求DF与面DBC所成角的正弦值．【答案】（I）证明见解析；（II）33【分析】（I）方法一：作DHAC⊥交

AC于H，连接BH，由题意可知DH⊥平面ABC，即有DHBC⊥，根据勾股定理可证得BCBH⊥，又//EFBC，可得DHEF⊥，BHEF⊥，即得EF⊥平面BHD，即证得EFDB⊥；（II）方法一：由//DFCH，所以DF与平面DBC所成角即为CH与平面DBC所成

角，作HGBD⊥于G，连接CG，即可知HCG即为所求角，再解三角形即可求出DF与平面DBC所成角的正弦值．【详解】（I）[方法一]：几何证法作DHAC⊥交AC于H，连接BH．∵平面ADFC⊥平面ABC，而平面ADFC平面ABCAC=，DH平面ADFC，∴DH⊥平面AB

C，而BC平面ABC，即有DHBC⊥．∵45ACBACD==，∴222CDCHBCCHBC===．在CBH中，22222cos45BHCHBCCHBCBC=+−=，即有222BHBCCH+=，∴BHBC⊥．由棱台的定

义可知，//EFBC，所以DHEF⊥，BHEF⊥，而BHDHH=，∴EF⊥平面BHD，而BD平面BHD，∴EFDB⊥．[方法二]【最优解】：空间向量坐标系方法作DOAC⊥交AC于O．∵平面ADFC⊥平面ABC，而平面ADFC平

面ABCAC=，DO平面ADFC，∴DO⊥平面ABC，以O为原点，建立空间直角坐标系如图所示.设OC=1,∵45ACBACD==，22DCBC==，∴22BC=,∴()()110,0,1,0,1,0,,,022DCB，∴11,,122BD=−

−,11,,022BC=−,11·044BDBC=−=,∴BC⊥BD,又∵棱台中BC//EF,∴EF⊥BD；[方法三]：三余弦定理法∵平面ACFD⊥平面ABC，∴1coscoscoscos45cos452BCDACBACD===,∴60BCD=

，又∵DC=2BC．∴90CBD=,即CBBD⊥,又∵//EFBC，∴EFDB⊥．（II）[方法一]：几何法因为//DFCH，所以DF与平面DBC所成角即为与CH平面DBC所成角．作HGBD⊥于G，连接CG，由（1）可知，

BC⊥平面BHD，因为所以平面BCD⊥平面BHD，而平面BCD平面BHDBD=，HG平面BHD，∴HG⊥平面BCD．即CH在平面DBC内的射影为CG，HCG即为所求角．在RtHGC△中，设BCa=，则2CHa=，2233BHDHaaHGaBDa===，∴13s

in33HGHCGCH===．故DF与平面DBC所成角的正弦值为33．[方法二]【最优解】：空间向量坐标系法设平面BCD的法向量为(),,nxyz=,由（I）得11,,122BD=−−,11

,,022BC=−,∴11022,11022xyzxy−−+=−+=令1x=,则1y=,2z=,()1,1,1n=,()0,1,0OC=，13cos,3111?1nOC==++,由于//DFOC，∴直线DF与平面DBC所成角的正弦值为33．[方法三]：空间向

量法以{,,}CHCBCD为基底,不妨设22DCBC==，则3,2,45,45,60DBCHHCBHCDDCB=====(由（I）的结论可得）．设平面DBC的法向量为nxCHyCBzCD=++，则由0,0,nCDnCB==得240

,0,xyzxyz++=++=取1z=，得32nCHCBCD=−++．设直线DF与平面DBC所成角为，则直线HC与平面DBC所成角也为，由公式得||23sin3||||26HCnHCn===．[方法四]：三余弦定理法由45ACBACD==，可知

H在平面DBC的射影G在DCB的角平分线上．设直线DF与平面DBC所成角为，则HC与平面DBC所成角也为．由由（I）的结论可得60BCD=，由三余弦定理，得cos45cos30cos=，6cos3=从而3sin3=．[方法五]：等体积法

设H到平面DBC的距离为h，设1DH=,则261,2,,22HCDCBCBD====,设直线DF与平面DBC所成角为，由已知得HC与平面DBC所成角也为．由HDBCDHBCVV−−=，1121122sin601451322322hsin=,求得33

h=，所以333sin13hHC===．【整体评价】（I）的方法一使用几何方法证明，方法二利用空间直角坐标系方法，简洁清晰，通性通法，确定为最优解；方法三使用了两垂直角的三余弦定理得到60BCD=，进而证明，过程简洁，确定为最优解（II）的方法一使用几何做法，方法二

使用空间坐标系方法，为通性通法，确定为最优解；方法三使用空间向量的做法，避开了辅助线的求作；方法四使用三余弦定理法，最为简洁，确定为最优解；方法五采用等体积转化法，避免了较复杂的辅助线.13．（2020·山东·高考真题）如图，四棱锥P-ABCD的底面为正方形，PD⊥底面ABCD

．设平面PAD与平面PBC的交线为l．（1）证明：l⊥平面PDC；（2）已知PD=AD=1，Q为l上的点，求PB与平面QCD所成角的正弦值的最大值．【答案】（1）证明见解析；（2）63.【分析】（1）利用线面垂直的判定定理证得AD

⊥平面PDC，利用线面平行的判定定理以及性质定理，证得//ADl，从而得到l⊥平面PDC；（2）方法一：根据题意，建立相应的空间直角坐标系，得到相应点的坐标，设出点(,0,1)Qm，之后求得平面QCD的法向量以及向量PB的坐标，求得cos,nPB的最大值，即

为直线PB与平面QCD所成角的正弦值的最大值.【详解】（1）证明：在正方形ABCD中，//ADBC，因为AD平面PBC，BC平面PBC，所以//AD平面PBC，又因为AD平面PAD，平面PAD平面PBCl=，所以//ADl，因为在

四棱锥PABCD−中，底面ABCD是正方形，所以,,ADDClDC⊥⊥且PD⊥平面ABCD，所以,,ADPDlPD⊥⊥因为CDPDD=，所以l⊥平面PDC．（2）［方法一］【最优解】：通性通法因为,,DPDADC两两垂直，建立空间直角坐标系Dxyz

−，如图所示：因为1PDAD==，设(0,0,0),(0,1,0),(1,0,0),(0,0,1),(1,1,0)DCAPB，设(,0,1)Qm，则有(0,1,0),(,0,1),(1,1,1)DCDQmPB===−，设平面

QCD的法向量为(,,)nxyz=，则00DCnDQn==，即00ymxz=+=，令1x=，则zm=−，所以平面QCD的一个法向量为(1,0,)nm=−，则210cos,31nPBmnPBnPBm++

==+根据直线的方向向量与平面法向量所成角的余弦值的绝对值即为直线与平面所成角的正弦值，所以直线PB与平面QCD所成角的正弦值等于2|1||cos,|31mnPBm+=+ruur223123

1mmm++=+223232||361111313133mmmm=+++=++，当且仅当1m=时取等号，所以直线PB与平面QCD所成角的正弦值的最大值为63.［方法二］：定义法如图2，因为l平面PBC，Ql，所以Q平面PBC．在平面PQ

C中，设PBQCE=．在平面PAD中，过P点作PFQD⊥，交QD于F，连接EF．因为PD⊥平面,ABCDDC平面ABCD，所以DCPD⊥．又由,,DCADADPDDPD⊥=平面PAD，AD平面PAD，所以DC⊥平面PAD．又PF平面PAD，所以D

CPF⊥．又由,,PFQDQDDCDQD⊥=平面,QOCDC平面QDC，所以PF⊥平面QDC，从而FEP即为PB与平面QCD所成角．设PQa=，在PQD△中，易求21aPFa=+．由PQEV与BEC相似，得1PEPQaEBBC==，可得31aPEa=+．所以22211226si

n1313333aaFEPaa+==+=++，当且仅当1a=时等号成立．［方法三］：等体积法如图3，延长CB至G，使得BGPQ=，连接GQ，GD，则//PBQG，过G点作GM⊥平面QDC，交平面QDC于M，连接QM，则GQM即为

所求．设PQx=，在三棱锥QDCG−中，111()(1)326QDCGVPDCDCBBGx−=+=+．在三棱锥GQDC−中，2111113232GQDCVGMCDQDGMx−==+．由QDCGGQDCVV−−=得2111(1)1632xGMx+=+，解得222211

2212111xxxxGMxxx+++===++++，当且仅当1x=时等号成立．在RtPDB△中，易求3PBQG==，所以直线PB与平面QCD所成角的正弦值的最大值为26sin33MQG==．【整体点评】（2）方法一：

根据题意建立空间直角坐标系，直线PB与平面QCD所成角的正弦值即为平面QCD的法向量n与向量PB的夹角的余弦值的绝对值，即cos,nPB，再根据基本不等式即可求出，是本题的通性通法，也是最优解；方法二：利用直线与平

面所成角的定义，作出直线PB与平面QCD所成角，再利用解三角形以及基本不等式即可求出；方法三：巧妙利用//PBQG，将线转移，再利用等体积法求得点面距，利用直线PB与平面QCD所成角的正弦值即为点面距与线段长度的比值的方法，即可求出．14．（2020·全国·高考真题）

如图，已知三棱柱ABC-A1B1C1的底面是正三角形，侧面BB1C1C是矩形，M，N分别为BC，B1C1的中点，P为AM上一点，过B1C1和P的平面交AB于E，交AC于F.（1）证明：AA1∥MN，且

平面A1AMN⊥EB1C1F；（2）设O为△A1B1C1的中心，若AO∥平面EB1C1F，且AO=AB，求直线B1E与平面A1AMN所成角的正弦值.【答案】（1）证明见解析；（2）1010.【分析】（1）由,MN分别为BC，11BC的中点，1//

MNCC，根据条件可得11//AABB，可证1MNAA//，要证平面11EBCF⊥平面1AAMN，只需证明EF⊥平面1AAMN即可；（2）连接NP，先求证四边形ONPA是平行四边形，根据几何关系求得EP，在11BC截取1BQEP=，由（1）BC⊥平面1AAMN，可得QPN为1B

E与平面1AAMN所成角，即可求得答案.【详解】（1）,MN分别为BC，11BC的中点，1//MNBB，又11//AABB，1//MNAA，在ABC中，M为BC中点，则BCAM⊥，又侧面11BBCC为矩形，1BCBB⊥，1//MNBB，MNBC⊥，由

MNAMM=，,MNAM平面1AAMN，BC⊥平面1AAMN，又11//BCBC，且11BC平面ABC，BC平面ABC，11//BC平面ABC，又11BC平面11EBCF，且平面11EBCF平面ABCEF=11//BCEF，//EFBC，又BC⊥平面1AAMN，EF⊥平

面1AAMN，EF平面11EBCF，平面11EBCF⊥平面1AAMN.(2)[方法一]：几何法如图，过O作11BC的平行线分别交1111,ABAC于点11,EF，联结11,,,AEAOAFNP，由于//

AO平面11EBCF，11//EF平面11EBCF，11=AOEFO，AO平面11AEF，11EF平面11AEF，所以平面11//AEF平面11EBCF．又因平面11AEF平面111=AABBAE，平面1

1EBCF平面111=AABBEB，所以11∥EBAE．因为111BCAN⊥，11BCMN⊥，1ANMNN=，所以11BC⊥面1AANM．又因1111∥EFBC，所以11⊥EF面1AANM，所以1AE与平面1AANM所成的角为1EAO．令2AB=，则11=NB，由于O为111ABC△的

中心，故112233==OENB．在1RtAEO中，122,3===AOABOE，由勾股定理得22112103=+=AEAOOE．所以11110sin10==EOEAOAE．由于11∥EBAE，直线1BE与平面1AAMN所成角的正弦值也为101

0．[方法二]【最优解】：几何法因为//AO平面11EFCB，平面11EFCB平面1=AMNANP，所以∥AONP．因为//ONAP，所以四边形OAPN为平行四边形．由（Ⅰ）知EF⊥平面1AMNA，则EF为平面1AMNA的垂线．所以1BE在平面1AMNA的射影为NP

．从而1BE与NP所成角的正弦值即为所求．在梯形11EFCB中，设1EF=，过E作11EGBC⊥，垂足为G，则3==PNEG．在直角三角形1BEG中，1110sin1010==BEG．[方法三]：向量法由（Ⅰ）知，11

BC⊥平面1AAMN，则11BC为平面1AAMN的法向量．因为∥AO平面11EBCF，AO平面1AAMN，且平面1AAMN平面11EBCFPN=，所以//AOPN．由（Ⅰ）知11,=∥AAMNAAMN，即四边形APNO为平行四边形，则==AONPAB

．因为O为正111ABC△的中心，故13==APONAM．由面面平行的性质得111111,33=∥EFBCEFBC，所以四边形11EFCB为等腰梯形．由P，N为等腰梯形两底的中点，得11PNBC⊥，则11110,==++=PNBCEBEPPN

NB111111111623+−=−BCPNBCPNBC．设直线1BE与平面1AAMN所成角为，ABa=，则2111211121103sin1013===+aEBBCEBBCaaa．所以直线1BE与平面1AAMN所成角的正弦值1

010．[方法四]：基底法不妨设2===AOABAC，以向量1,,AAABAC为基底，从而11,,AAABAAAC=，,3=ABAC．1111123=++=+EBEAAAABABAA，BCACAB=−，则12103=EB，||2BC=．所以112()3=+−=EBBCAB

AAACAB2224333−=−ABACAB．由（Ⅰ）知BC⊥平面1AAMN，所以向量BC为平面1AAMN的法向量．设直线1BE与平面1AAMN所成角，则11110sincos,10||===EBBCEBBCEBBC．故直线1BE与平面1A

AMN所成角的正弦值为10sin10=．[方法五]：坐标法过O过底面ABC的垂线，垂足为Q，以Q为坐标原点建立如图所示空间直角坐标系，设OAM=，AO=AB=2，则()()131,,2sin,0,2

cos,0,1,32cos,03BAB−−，所以11313,,0,,2cos,033333AEABE==−，所以12,2cos,2sin,3BE=−−−易得

()1,0,0n=r为平面A1AMN的一个法向量，则直线B1E与平面A1AMN所成角的正弦值为1112103cos,10449nBEnBEnBE===+【整体点评】(2)方法一：几何法的核心在于找到线面角，本题中利用平行关系进行等价转化是解决问题的关键；方法二：等价转化是解决问题的关键

，构造直角三角形是求解角度的正弦值的基本方法；方法三：利用向量法的核心是找到平面的法向量和直线的方向向量，然后利用向量法求解即可；方法四：基底法是立体几何的重要思想，它是平面向量基本定理的延伸，其关键之处在于找到平面的法向量

和直线的方向向量.方法五：空间坐标系法是立体几何的重要方法，它是平面向量的延伸，其关键之处在于利用空间坐标系确定位置，找到平面的法向量和直线的方向向量.15．（2019·天津·高考真题）如图，在四棱锥PABCD−中，底面ABCD

为平行四边形，PCD为等边三角形，平面PAC⊥平面PCD，PACD⊥，2CD=，3AD=，（Ⅰ）设GH，分别为PBAC，的中点，求证：GH平面PAD；（Ⅱ）求证：PA⊥平面PCD；（Ⅲ）求直线AD与平面PAC所成角的正弦值.【答案】（I）见解析

；（II）见解析；（III）33.【分析】（I）连接BD，结合平行四边形的性质，以及三角形中位线的性质，得到GHPD，利用线面平行的判定定理证得结果；（II）取棱PC的中点N，连接DN，依题意，得DNPC⊥，结合面

面垂直的性质以及线面垂直的性质得到DNPA⊥，利用线面垂直的判定定理证得结果；（III）利用线面角的平面角的定义得到DAN为直线AD与平面PAC所成的角，放在直角三角形中求得结果.【详解】（I）证明：连接BD，易知ACBDH=，BHDH=，又由BG=PG，故GHPD，又因为GH平

面PAD，PD平面PAD，所以GH平面PAD.（II）证明：取棱PC的中点N，连接DN，依题意，得DNPC⊥，又因为平面PAC⊥平面PCD，平面PAC平面PCDPC=，所以DN⊥平面PAC，又PA平面PAC，故D

NPA⊥，又已知PACD⊥，CDDND=，所以PA⊥平面PCD.（III）解：连接AN，由（II）中DN⊥平面PAC，可知DAN为直线AD与平面PAC所成的角.因为PCD为等边三角形，2CD=且N为PC的中点，所以3DN=，又DNAN⊥，在RtAND中

，3sin3DNDANAD==，所以，直线AD与平面PAC所成角的正弦值为33.【点睛】本小题主要考查直线与平面平行、直线与平面垂直、平面与平面垂直、直线与平面所成的角等基础知识，考查空间想象能力和推

理能力.16．（2019·浙江·高考真题）如图，已知三棱柱111ABCABC-，平面11AACC⊥平面ABC,90ABC=，1130,,,BACAAACACEF===分别是11,ACAB的中点.（1）证明：EFBC⊥；（2）求直线EF与平面1ABC所成角的余弦值.【答案】（1）证明见解析

；（2）35.【分析】(1)由题意首先证得线面垂直，然后利用线面垂直的定义即可证得线线垂直；(2)建立空间直角坐标系，分别求得直线的方向向量和平面的法向量，然后结合线面角的正弦值和同角三角函数基本关系可得线面角的余弦值.【

详解】(1)如图所示，连结11,AEBE，等边1AAC△中，AEEC=，则1AEAC⊥，平面ABC⊥平面11AACC，且平面ABC∩平面11AACCAC=，由面面垂直的性质定理可得：1AE⊥平面ABC，故1AEBC⊥，由三棱柱的性质可知11ABAB∥，而ABBC⊥，故

11ABBC⊥，且1111ABAEA=，由线面垂直的判定定理可得：BC⊥平面11ABE，结合EF⊆平面11ABE，故EFBC⊥.(2)在底面ABC内作EH⊥AC，以点E为坐标原点，EH,EC,1EA方向分别为x,y,z轴正方向建立空间直角坐标系Exyz−.设

1EH=，则3AEEC==，1123AACA==,3,3BCAB==，据此可得：()()()1330,3,0,,,0,0,0,3,0,3,022ABAC−，由11ABAB=可得点1B的坐标为133,3,322B，利用中点坐标公式可得：33,3

,344F，由于()0,0,0E，故直线EF的方向向量为：33,3,344EF=设平面1ABC的法向量为(),,mxyz=，则：()()13333,,,,33022223333,,,,002222mABxyzxyzmBCxyzxy=−=+−=

=−=−+=，据此可得平面1ABC的一个法向量为()1,3,1m=，33,3,344EF=此时64cos,53552EFmEFmEFm===，设直线EF与平面1ABC所成角

为，则43sincos,,cos55EFm===.【点睛】本题考查了立体几何中的线线垂直的判定和线面角的求解问题，意在考查学生的空间想象能力和逻辑推理能力；解答本题关键在于能利用直线与直线、直线与平面、平面与平面关系的相互转化，通过严密推理，同时对于立体几何中角的

计算问题，往往可以利用空间向量法，通过求解平面的法向量，利用向量的夹角公式求解.17．（2018·江苏·高考真题）如图，在正三棱柱ABC-A1B1C1中，AB=AA1=2，点P，Q分别为A1B1，BC的中点。（1）求异面直线BP与AC1所成角的余弦值；（2）求直线CC1与平面A

QC1所成角的正弦值【答案】（1）31020（2）55【详解】分析：（1）先建立空间直角坐标系，设立各点坐标，根据向量数量积求得向量1,BPAC的夹角，再根据向量夹角与异面直线所成角的关系得结果；（2）利用平面的方向量的求法列方程组解得平面1AQC的

一个法向量，再根据向量数量积得向量夹角，最后根据线面角与所求向量夹角之间的关系得结果.详解：如图，在正三棱柱ABC−A1B1C1中，设AC，A1C1的中点分别为O，O1，则OB⊥OC，OO1⊥OC，OO1⊥OB，以1,,OBOCOO为基底，建立

空间直角坐标系O−xyz．因为AB=AA1=2，所以()()()()()()1110,1,0,3,0,0,0,1,0,0,1,2,3,0,2,0,1,2ABCABC−−．（1）因为P为A1B1的中点，所以31,,222P−，从而()131,,2,0,2,222BPAC=−

−=，故11114310,20522BPACcosBPACBPAC−+===．因此，异面直线BP与AC1所成角的余弦值为31020．（2）因为Q为BC的中点，所以31,,022Q，因此33,,022AQ=，()()110,2,2,0,0,2ACCC

==．设n=（x，y，z）为平面AQC1的一个法向量，则10,0,AQnACn==即330,22220.xyyz+=+=不妨取()3,1,1n=−，设直线CC1与平面AQC1所成角为，则11125sin,55

2CCncosCCnCCn====，所以直线CC1与平面AQC1所成角的正弦值为55．点睛：本题考查空间向量、异面直线所成角和线面角等基础知识，考查运用空间向量解决问题的能力.利用法向量求解空间线面角的关键在于“四破”：第一，破“

建系关”，构建恰当的空间直角坐标系；第二，破“求坐标关”，准确求解相关点的坐标；第三，破“求法向量关”，求出平面的法向量；第四，破“应用公式关”.18．（2018·浙江·高考真题）如图，已知多面体111111,,,ABCABCAABBCC−均垂直于平面111,120,4,1,2ABCAB

CAACCABBCBB======．（Ⅰ）求证：1AB⊥平面111ABC；（Ⅱ）求直线1AC与平面1ABB所成角的正弦值．【答案】（Ⅰ）证明见解析；（Ⅱ）3913.【分析】（Ⅰ）方法一：通过计算，根据勾股定理得111111,ABABABBC⊥⊥,再根据线面垂直的判定定理得结论；

（Ⅱ）方法一：找出直线AC1与平面ABB1所成的角，再在直角三角形中求解即可.【详解】（Ⅰ）［方法一］：几何法由11112,4,2,,ABAABBAAABBBAB===⊥⊥得11122ABAB==，所以2221111ABABAA+=，即有111ABAB⊥.由2BC=，112,1,BBCC==11,

BBBCCCBC⊥⊥得115BC=，由2,120ABBCABC===得23AC=，由1CCAC⊥，得113AC=，所以2221111ABBCAC+=，即有111ABBC⊥，又11111ABBCB=，因此1AB⊥平面111ABC.［方法二］：

向量法如图，以AC的中点O为原点，分别以射线OB，OC为x，y轴的正半轴，建立空间直角坐标系O-xyz.由题意知各点坐标如下：()()()()()1110,3,0,1,0,0,0,3,4,1,0,2,0,3,1,ABABC

−−因此11111(1,3,2),(1,3,2),(0,23,3)ABABAC==−=−,由1110ABAB=得111ABAB⊥；由1110ABAC=得111ABAC⊥，所以1AB⊥平面111ABC.（Ⅱ）［方法一］：定义法如图，过点1C作111CDAB⊥，交直

线11AB于点D，连结AD.由1AB⊥平面111ABC得平面111ABC⊥平面1ABB，由111CDAB⊥得1CD⊥平面1ABB，所以1CAD是1AC与平面1ABB所成的角.由1111115,22,21BCABAC===得11111161cos,sin77CABCAB=

=，所以13CD=，故11139sin13CDCADAC==.因此，直线1AC与平面1ABB所成的角的正弦值是3913.［方法二］：向量法设直线1AC与平面1ABB所成的角为.由(I)可知11(0,23,1),(1

,3,0),(0,0,2)ACABBB===,设平面1ABB的法向量(,,)nxyz=.由100nABnBB==即3020xyz+==，可取(3,1,0)n=−，所以11139si

ncos,13||ACnACnACn===.因此，直线1AC与平面1ABB所成的角的正弦值是3913.［方法三］：【最优解】定义法+等积法设直线1AC与平面1ABB所成角为，点1C到平面1ABB距离为d（下同）．因为1

CC∥平面1ABB，所以点C到平面1ABB的距离等于点1C到平面1ABB的距离．由条件易得，点C到平面1ABB的距离等于点C到直线AB的距离，而点C到直线AB的距离为3，所以3d=．故1339sin1313dAC===．［方法四］：定义法+等积法设直线1AC与平面1A

BB所成的角为，由条件易得11111122,5,21ABBCAC===，所以222111111111111110cos25ABBCACABCABBC+−==−，因此11115sin5ABC=．于是得111

11111111sin62ABCSABBCABC==△，易得114AABS=△．由111111CAABAABCVV−−=得1111111133AABABCSdSAB=△△，解得3d=．故1339sin

1313dAC===．［方法五］：三正弦定理的应用设直线1AC与平面1ABB所成的角为，易知二面角11CAAB−−的平面角为6BAC=，易得1123sin13CAA=，所以由三正弦定理得1123139sinsinsin21313C

AABAC===．［方法六］：三余弦定理的应用设直线1AC与平面1ABB所成的角为，如图2，过点C作CGAB⊥，垂足为G，易得CG⊥平面1ABB，所以CG可看作平面1ABB的一个法向量．结合三余弦定理得1123339sinco

s,coscos131323ACCGCACGCA====．［方法七］：转化法＋定义法如图3，延长线段1AA至E，使得1AECC=．联结CE，易得1ECAC∥，所以1AC与平面1ABB所成角等于直线EC与平面1ABB所成角．过点C作CGAB⊥，垂足为G，联结GE，易得CG⊥平面1A

BB，因此EG为EC在平面1ABB上的射影，所以CEG为直线EC与平面1ABB所成的角．易得13CE=，3CG=，因此339sin1313CGCEGCE===．［方法八］：定义法＋等积法如图4，延

长11,ABAB交于点E，易知2BE=，又2ABBC==，所以ACCE⊥，故CE⊥面11AACC．设点1C到平面1ABB的距离为h，由1111EAACCAAEVV−−=得1111113232AAAEhAAACCE=，解得3h

=．又113AC=，设直线1AC与平面1ABB所成角为，所以339sin1313==．【整体点评】（Ⅰ）方法一：通过线面垂直的判定定理证出，是该题的通性通法；方法二：通过建系，根据数量积为零，证出；（Ⅱ）方法一：根据线面角的定义以及几何法求线面角的步骤，“一作二证三计算”解出；方法二：根

据线面角的向量公式求出；方法三：根据线面角的定义以及计算公式，由等积法求出点面距，即可求出，该法是本题的最优解；方法四：基本解题思想同方法三，只是求点面距的方式不同；方法五：直接利用三正弦定理求出；方法六：直接利用三

余弦定理求出；方法七：通过直线平移，利用等价转化思想和线面角的定义解出；方法八：通过等价转化以及线面角的定义，计算公式，由等积法求出点面距，即求出．19．（2018·全国·高考真题）如图，四边形ABCD为正方形，,EF分别为,

ADBC的中点，以DF为折痕把DFC折起，使点C到达点P的位置，且PFBF⊥.（1）证明：平面PEF⊥平面ABFD；（2）求DP与平面ABFD所成角的正弦值.【答案】（1）证明见解析；（2）34.【分析】（1）依题可知BFPF⊥

，BFEF⊥，利用线面垂直的判定定理可得BF⊥平面PEF，再利用面面垂直的判定定理即可证出平面PEF⊥平面ABFD；（2）方法一：依题意建立相应的空间直角坐标系，求得平面ABFD的法向量，设DP与平面ABFD所成角为，利用线面角的向量公式即可求出．【详解】（1）由已知可得，BFPF

⊥，BFEF⊥，又PFEFF=，所以BF⊥平面PEF.又BF平面ABFD，所以平面PEF⊥平面ABFD；（2）[方法一]：向量法作PHEF⊥，垂足为H.由（1）得，PH⊥平面ABFD.以H为坐标原点，HF的方向为y轴正方向，设1BF=，建立如图所示的空间直角坐标系Hxyz−.由（1）可得，DE

PE⊥.又2DP=，1DE=，所以3PE=.又1PF=，2=EF，故PEPF⊥，可得33,22PHEH==.则()33330,0,0,0,0,,1,,0,1,,,2222DHPDP−−=30,0,2HP=为平面ABFD的法向量.设D

P与平面ABFD所成角为，则334sin43HDPDPHPP===uuuuuruuuruuruur.所以DP与平面ABFD所成角的正弦值为34.[方法2]：向量法如图3所示以E为原点建系．设正方形边长为2，由（1）知，BF⊥平面PEF，则DE⊥平面PEF，故DEPE⊥

．易求3PE=，则点P到直线EF的距离为32，从而330,,22P．又(1,0,0)D−，故331,,22DP=，而平面ABFD的一个法向量(0,0,1)n=，故DP与平面ABFD所成角的正弦值332sin|cos,|24DPnDPnDPn=

===．[方法3]：【最优解】定义法如图4，作PHEF⊥，垂足为H，联结DH．由（1）知，PH⊥平面ABFD,因此PDH为DP与平面ABFD所成的角．设正方形ABCD的边长为2，则1DE=，在RtPED△中，3PE=．又因为1,2PF

EF==，由222PEPFEF+=知，390,2EPFPH==．又因为2PD=，所以在RtPHD△中，3sin4PHPDHPD==．所以DP与平面ABFD所成角的正弦值为34．[方法4]：等积法不妨设=2AB，则1,3,2DEPEDPEF====

．PEPF⊥，又,PFPDPDPEP⊥=，所以PF⊥平面PDE．设点P到平面DEF的距离为d，根据=FPDEPDEFVV−−，即1111131213232d=，解得32d=．于是PD与平面ABFD所成角的正弦值为34dDP=．【整体点评

】（2）方法一：建立空间直角坐标系利用线面角的向量公式求解，可算作通性通法；方法二：同方法一，只是建系方式不一样；方法三：利用线面角的定义求解，计算量小，是该题的最优解；方法四：利用等积法求出点P到平面DEF的距离，再根据线面角的正弦公式即可求出，是线面角的常见求法．20．（

2018·天津·高考真题）如图，在四面体ABCD中，△ABC是等边三角形，平面ABC⊥平面ABD，点M为棱AB的中点，AB=2，AD=23，∠BAD=90°．（Ⅰ）求证：AD⊥BC；（Ⅱ）求异面直线BC与MD所成角的余

弦值；（Ⅲ）求直线CD与平面ABD所成角的正弦值．【答案】(Ⅰ)证明见解析；(Ⅱ)1326；(Ⅲ)34．【详解】分析：（Ⅰ）由面面垂直的性质定理可得AD⊥平面ABC，则AD⊥BC．（Ⅱ）取棱AC的中点N，连接MN，ND．由几何关系可知∠DMN

（或其补角）为异面直线BC与MD所成的角．计算可得113226MNcosDMNDM==．则异面直线BC与MD所成角的余弦值为1326．（Ⅲ）连接CM．由题意可知CM⊥平面ABD．则∠CDM为直线CD与平面ABD所成的角．计算可得34CMsinCDMC

D==．即直线CD与平面ABD所成角的正弦值为34．详解：（Ⅰ）证明：由平面ABC⊥平面ABD，平面ABC∩平面ABD=AB，AD⊥AB，可得AD⊥平面ABC，故AD⊥BC．（Ⅱ）取棱AC的中点N，连接

MN，ND．又因为M为棱AB的中点，故MN∥BC．所以∠DMN（或其补角）为异面直线BC与MD所成的角．在Rt△DAM中，AM=1，故DM=22=13ADAM+．因为AD⊥平面ABC，故AD⊥AC．在Rt△DAN中，AN=1，故DN=22=13ADAN+．在等腰三角形DMN中，MN=1，可

得1132cos26MNDMNDM==．所以，异面直线BC与MD所成角的余弦值为1326．（Ⅲ）连接CM．因为△ABC为等边三角形，M为边AB的中点，故CM⊥AB，CM=3．又因为平面ABC⊥平面A

BD，而CM平面ABC，故CM⊥平面ABD．所以，∠CDM为直线CD与平面ABD所成的角．在Rt△CAD中，CD=22ACAD+=4．在Rt△CMD中，3sin4CMCDMCD==．所以，直线CD与平面ABD所成角的正弦值为34．点睛：本小题主要考查异面直线所成的角、直线与

平面所成的角、平面与平面垂直等基础知识．考查空间想象能力、运算求解能力和推理论证能力．21．（2017·上海·高考真题）如图，直三棱柱111ABCABC-的底面为直角三角形，两直角边AB和AC的长分别为4和2，侧棱1AA的长为5.（1）求三棱柱111ABCABC-的体积；（2）设M

是BC中点，求直线1AM与平面ABC所成角的大小.【答案】（1）20;（2）arctan5【分析】（1）三棱柱111ABCABC−的体积11ABCVSAAACAA=，由此能求出结果；（2）连结1,AMAMA是直线1AM与平面ABC所成角

，由此能求出直线1AM与平面ABC所成角的大小.【详解】解：（1）∵直三棱柱ABC﹣A1B1C1的底面为直角三角形，两直角边AB和AC的长分别为4和2，侧棱AA1的长为5．∴三棱柱ABC﹣A1B1C1的体积：V＝S△ABC×AA1112

ABACAA=14252==20．（2）连结AM，∵直三棱柱ABC﹣A1B1C1的底面为直角三角形，两直角边AB和AC的长分别为4和2，侧棱AA1的长为5，M是BC中点，∴AA1⊥底面ABC，AM11164522BC==+=，∴∠A1MA是直线A1

M与平面ABC所成角，tan∠A1MA1555AAAM===，∴直线A1M与平面ABC所成角的大小为arctan5．【点睛】本题考查三棱柱的体积的求法，考查线面角的大小的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查

推理论证能力、运算求解能力、空间想象能力，考查化归与转化思想、函数与方程思想、数形结合思想，是中档题．22．（2017·天津·高考真题）如图，在四棱锥PABCD−中，AD⊥平面PDC，ADBC，PDPB

⊥，1AD=，3BC=，4CD=，2PD=.（I）求异面直线AP与BC所成角的余弦值；（II）求证：PD⊥平面PBC；（Ⅲ）求直线AB与平面PBC所成角的正弦值.【答案】（Ⅰ）55.（Ⅱ）见解析;（Ⅲ）55.【分析】（Ⅰ）由已知AD//BC，故DAP或其补角即为异面直线AP与B

C所成的角，然后在Rt△PDA中求解即可；（Ⅱ）因为AD⊥平面PDC，所以AD⊥PD，PD⊥BC，又PD⊥PB，所以PD⊥平面PBC；（Ⅲ）过点D作AB的平行线交BC于点F，连结PF，则DF与平面PBC所成的角等于AB与平面PBC所成的角，且DFP

为直线DF和平面PBC所成的角，然后在Rt△DPF中求解即可.【详解】解：（Ⅰ）如图，由已知AD//BC，故DAP或其补角即为异面直线AP与BC所成的角.因为AD⊥平面PDC，所以AD⊥PD.在Rt△PDA中，由已知，

得225APADPD=+=，故5cos5ADDAPAP==.所以，异面直线AP与BC所成角的余弦值为55.（Ⅱ）证明：因为AD⊥平面PDC，直线PD平面PDC，所以AD⊥PD.又因为BC//AD，所以PD⊥BC

，又PD⊥PB，BCPBB=所以PD⊥平面PBC.（Ⅲ）过点D作AB的平行线交BC于点F，连结PF，则DF与平面PBC所成的角等于AB与平面PBC所成的角.因为PD⊥平面PBC，故PF为DF在平面P

BC上的射影，所以DFP为直线DF和平面PBC所成的角.由于AD//BC，DF//AB，故BF=AD=1，由已知，得CF=BC–BF=2.又AD⊥DC，故BC⊥DC，在Rt△DCF中，可得2225DFCDCF=+=,在Rt△DPF中，可得5sin5PDDFPDF==

.所以，直线AB与平面PBC所成角的正弦值为55.考点：两条异面直线所成的角、直线与平面垂直、直线与平面所成的角【点睛】本小题主要考查两条异面直线所成的角、直线与平面垂直的证明、直线与平面所成的角，要求一定的空间想象能力、运算求解能力和推理论证能力.求两

条异面直线所成的角，首先要借助平行线找出异面直线所成的角，证明线面垂直只需寻求线线垂直，求线面角首先利用转化思想寻求直线与平面所成的角，然后再计算即可.23．（2017·浙江·高考真题）如图，已知四棱锥P-ABCD，△PAD是以AD为斜边的等腰直角三角形，BC∥

AD，CD⊥AD，PC=AD=2DC=2CB,E为PD的中点.（I）证明：CE∥平面PAB；（II）求直线CE与平面PBC所成角的正弦值【答案】（I）见解析；（II）28.【详解】试题分析：本题主要考查空间点、线、面位置关系，直线与平面所成的角等基础知识，同时考查空间想象能力和运算求解能

力．满分15分．（Ⅰ）取PA中点F，构造平行四边形BCEF，可证明；（Ⅱ）由题意，取BC，AD的中点M，N，可得AD⊥平面PBN，即BC⊥平面PBN，过点Q作PB的垂线，垂足为H，连结MH．可知MH是MQ在平面PBC上的射影，所以∠QMH是直线CE与平面PBC所成的角．依此可在R

t△MQH中，求∠QMH的正弦值．试题解析：（Ⅰ）如图，设PA中点为F，连接EF，FB．因为E，F分别为PD，PA中点，所以//EFAD且12EFAD=，又因为//BCAD，12BCAD=，所以//EFBC且EFBC=，即四边形BCEF为平行四边形，所以//CEBF，因此//CE平面PAB．（

Ⅱ）分别取BC，AD的中点为M，N．连接PN交EF于点Q，连接MQ．因为E，F，N分别是PD，PA，AD的中点，所以Q为EF中点，在平行四边形BCEF中，MQ//CE．由△PAD为等腰直角三角形得PN⊥AD．由DC⊥AD，N是AD的中点得BN⊥AD．所以AD⊥平面PBN，由BC//AD得BC⊥

平面PBN，那么平面PBC⊥平面PBN．过点Q作PB的垂线，垂足为H，连接MH．MH是MQ在平面PBC上的射影，所以∠QMH是直线CE与平面PBC所成的角．设CD=1．在△PCD中，由PC=2，CD=1，PD=2得CE=2，在△PBN中，由PN=BN=1，PB

=3得QH=14，在Rt△MQH中，QH=14，MQ=2，所以sin∠QMH=28，所以直线CE与平面PBC所成角的正弦值是28．【名师点睛】本题主要考查线面平行的判定定理、线面垂直的判定定理及面面垂直的判定定理，属于中档题．证明线面平行的常用方法：①利用线面平行的判定定理，使用

这个定理的关键是设法在平面内找到一条与已知直线平行的直线，可利用几何体的特征，合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行．②利用面面平行的性质，即两平面平行，在其中一平面内的直线平行于另一平面．本题（

1）是就是利用方法①证明的．另外，本题也可利用空间向量求解线面角．24．（2017·北京·高考真题）如图，在四棱锥PABCD−中，底面ABCD为正方形，平面PAD⊥平面ABCD，点M在线段PB上，PD平面MAC，6PAPD==，4AB=．（1）求证：M为PB的中点；（2）

求二面角BPDA−−的大小；（3）求直线MC与平面BDP所成角的正弦值．【答案】（1）证明见解析；（2）3；（3）269．【分析】（1）设AC，BD的交点为E，由线面平行性质定理得PDME，再根据三角形中位线性质得M为PB的中点．（2）先根据条件

建立空间直角坐标系，设立各点坐标，列方程组解各面法向量，根据向量数量积求向量夹角，最后根据二面角与向量夹角相等或互补关系求二面角大小（3）先根据条件建立空间直角坐标系，设立各点坐标，列方程组解各面法向量，根据向量数量积求向量夹角，最后根据线

面角与向量夹角互余关系求线面角大小【详解】（1）设AC，BD的交点为E，连接ME．因为PD平面MAC，平面MAC平面PDBME=，所以PDME．因为ABCD是正方形，所以E为BD的中点，所以M为PB的中点．（2）取AD的中点O，连接OP，OE．因为P

APD=，所以OPAD⊥．又平面PAD⊥平面ABCD，且OP平面PAD，所以OP⊥平面ABCD．因为OE平面ABCD，所以OPOE⊥．因为ABCD是正方形，所以OEAD⊥．如图，建立空间直角坐标系Oxy

z−，则()0,0,2P，()2,0,0D，()2,4,0B−，所以()4,4,0BD=−，()2,0,2PD=−．设平面BDP的法向量为(),,nxyz=，则00nBDnPD==，即440220xyxz−=−=

．令1x=，则1y=，2z=，于是()1,1,2n=．平面PAD的法向量为()0,1,0p=，所以1cos,2npnpnp==．由题知二面角BPDA−−为锐角，所以它的大小为3．（3）由题意知21,2,2M−，()2,4,0C

，23,2,2MC=−．设直线MC与平面BDP所成角为，则26sincos,9nMCnMCnMC===．所以直线MC与平面BDP所成角的正弦值为269．25．（2016·浙江·高考真题）如图，在三棱台ABC–DEF中，平

面BCFE⊥平面ABC，∠ACB=90°，BE=EF=FC=1，BC=2，AC=3.（Ⅰ）求证：BF⊥平面ACFD；（Ⅱ）求直线BD与平面ACFD所成角的余弦值.【答案】（1）证明详见解析；（2）217.【详解】试题分析：本题主要考查空

间点、线、面位置关系，线面角等基础知识，同时考查空间想象能力和运算求解能力．试题解析：（Ⅰ）延长,,ADBECF相交于一点K，如图所示.因为平面BCFE⊥平面ABC，且ACBC⊥，所以AC⊥平面BCK，因此，BFAC⊥.又因为//EFBC，1BEEFFC===，2BC=，所

以BCK为等边三角形，且F为CK的中点，则BFCK⊥所以BF⊥平面ACFD.（Ⅱ）因为BF⊥平面ACK，所以BDF是直线BD与平面ACFD所成的角.在RtBFD中，33,2BFDF==，得21cos7BDF=.所以，直线BD与平面ACFD所成的角的余弦值为217

.【考点】空间点、线、面位置关系、线面角.【方法点睛】解题时一定要注意直线与平面所成的角的范围，否则很容易出现错误．证明线面垂直的关键是证明线线垂直，证明线线垂直常用的方法是直角三角形、等腰三角形的“三线合一”和菱形、正方形的对角线．26．（2016·天津·高考真题）如图，正方形

ABCD的中心为O，四边形OBEF为矩形，平面OBEF⊥平面ABCD，点G为AB的中点，AB=BE=2.（Ⅰ）求证：EG∥平面ADF；（Ⅱ）求二面角O−EF−C的正弦值；（Ⅲ）设H为线段AF上的点，且AH=23HF，求直线BH和平面CE

F所成角的正弦值.【答案】（Ⅰ）详见解析；（Ⅱ）33；（Ⅲ）721.【详解】试题分析：（Ⅰ）利用空间向量证明线面平行，关键是求出平面的法向量，利用法向量与直线方向向量垂直进行论证；（Ⅱ）利用空间向量求二面角，关键是求出平面的法向量，再利用向量数量积求出法向量夹角，最后根据向量夹角与二面角相等或互

补关系求正弦值；（Ⅲ）利用空间向量求线面角，关键是求出平面的法向量，再利用向量数量积求出向量夹角，最后根据向量夹角与线面角互余关系求正弦值.试题解析：依题意，OFABCD⊥平面，如图，以O为点，分别以,,ADBAOF的方向为

x轴、y轴、z轴的正方向建立空间直角坐标系，依题意可得(0,0,0)O，()1,1,0,(1,1,0),(1,1,0),(11,0),(1,1,2),(0,0,2),(1,0,0)ABCDEFG−−−−−−−，.（Ⅰ）证明：依题意，()(2,0,0),1,1,2ADAF==−.设()1,,n

xyz=为平面ADF的法向量，则110{0nADnAF==，即20{20xxyz=−+=.不妨设1z=，可得()102,1n=,，又()0,1,2EG=−，可得10EGn=，又因为直线EGADF平面，所以//EGADF平面.（Ⅱ）

解：易证，()1,1,0OA=−为平面OEF的一个法向量.依题意，()()1,1,0,1,1,2EFCF==−.设()2,,nxyz=为平面CEF的法向量，则220{0nEFnCF==，即0{20xyxyz+=−+

+=.不妨设1x=，可得()21,1,1n=−.因此有2226cos,3OAnOAnOAn==−，于是23sin,3OAn=，所以，二面角OEFC−−的正弦值为33.（Ⅲ）解：由23AHHF=，得25AHAF=.因为，所以2224,,5555AHAF

==−，进而有334,,555H−，从而284,,555BH=，因此2227cos,21BHnBHnBHn==−.所以，直线BH和平面CEF所成角的正弦值为721.【考点】利用空间向量解决立体几何问题27．（201

6·全国·高考真题）如图，四棱锥P−ABCD中，PA⊥底面ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，N为PC的中点.（Ⅰ）证明MN∥平面PAB;（Ⅱ）求直线AN与平面PMN所成角的正弦值.

【答案】（Ⅰ）详见解析；（Ⅱ）8525．【详解】（Ⅰ）由已知得223AMAD==.取BP的中点T，连接,ATTN，由N为PC中点知TN//BC，122TNBC==.又//ADBC，故//TNAM，TNAM=，四边形AMNT为平行四边形，于是MNAT.因为AT平面PAB，MN平面PAB，所以/

/MN平面PAB.（Ⅱ）取BC的中点E，连结AE.由ABAC=得AEBC⊥，从而AEAD⊥，且222252BCAEABBEAB=−=−=.以A为坐标原点，AE的方向为x轴正方向，建立如图所示的空间直角坐标系|Axyz−.由题意知，(0),0,4P，(0

),2,0M，()50,2,C，522,1,N，(0,2,4)PM=−，5(,1,2)2PN=−，5(,1,2)2AN=.设(,,)nxyz=为平面PMN的一个法向量，则0,0,nPMnPN==即240,520,2yzxyz−=+−=可取(0,2,1)n

=.于是85cos,25nANnANnAN==.【考点】空间线面间的平行关系，空间向量法求线面角．【技巧点拨】（1）证明立体几何中的平行关系，常常是通过线线平行来实现，而线线平行常常利用三角形的中位线、平

行四边形与梯形的平行关系来推证；（2）求解空间中的角和距离常常可通过建立空间直角坐标系，利用空间向量中的夹角与距离来处理．28．（2016·北京·高考真题）如图，在四棱锥PABCD−中，平面PAD⊥平面ABCD，PAPD⊥，PAPD=，ABAD⊥，1AB=，2AD=

，5ACCD==.（1）求证：平面PAB；（2）求直线PA与平面PCD所成角的正弦值；（3）在棱上是否存在点，使得平面PCD？若存在，求的值；若不存在，说明理由.【答案】（1）见解析；（2）33；（3）存在，14AMAP=【详解】

试题分析：（1）由面面垂直性质定理知AB⊥平面；根据线面垂直性质定理可知，再由线面垂直判定定理可知平面；（2）取的中点，连结PO，CO，以为坐标原点建立空间直角坐标系Oxyz−，利用向量法可求出直线PB与平面PCD所成角的正弦值；（3）假设存在

，根据A，P，M三点共线，设，根据//BM平面PCD，即，求的值，即可求出AMAP的值.试题解析：（1）因为平面PAD⊥平面ABCD，ABAD⊥，所以平面，所以，又因为，所以平面；（2）取的中点，连结PO，CO，因为

PAPD=，所以.又因为平面，平面PAD⊥平面，所以平面.因为平面，所以CO.因为，所以.如图建立空间直角坐标系，由题意得，.设平面的法向量为，则即令，则.所以.又，所以.所以直线PB与平面所成角的正弦值为.（3）设是

棱上一点，则存在使得.因此点.因为平面，所以BM∥平面当且仅当，即，解得.所以在棱上存在点使得平面，此时.考点：1.空间垂直判定与性质；2.异面直线所成角的计算；3.空间向量的运用.29．（2016·天津·高考真题）如图

，四边形ABCD是平行四边形，平面AED⊥平面ABCD，EF||AB，AB=2，BC=EF=1，AE=6，DE=3，∠BAD=60º，G为BC的中点.（Ⅰ）求证：FG||平面BED；（Ⅱ）求证：平面BED⊥平面AED；（Ⅲ）求直线EF与平面BED所成角的正弦值.【答案】（Ⅰ）

详见解析（Ⅱ）详见解析（Ⅲ）【详解】试题分析：（Ⅰ）证明线面平行，一般利用线面平行判定定理，即从线线平行出发给予证明，而线线平行寻找与论证，往往结合平面几何知识，如本题构造一个平行四边形：取的中点为，可证四边形是平

行四边形，从而得出（Ⅱ）面面垂直的证明，一般转化为证线面垂直，而线面垂直的证明，往往需多次利用线面垂直判定与性质定理，而线线垂直的证明有时需要利用平面几何的知识，如本题可由余弦定理解出，即（Ⅲ）求线面

角，关键作出射影，即面的垂线，可利用面面垂直的性质定理得到线面垂直，即面的垂线：过点作于点，则平面，从而直线与平面所成角即为.再结合三角形可求得正弦值试题解析：（Ⅰ）证明：取的中点为，连接，在中，因为

是的中点，所以且，又因为，所以且，即四边形是平行四边形，所以，又平面，平面，所以平面.（Ⅱ）证明：在中，，由余弦定理可，进而可得，即，又因为平面平面平面；平面平面，所以平面.又因为平面，所以平面平面.（Ⅲ）解：因为，所以直线与平面所成角即为直线与平面所成角.过点作于点，连接，又因为平面平面，由（

Ⅱ）知平面，所以直线与平面所成角即为.在中，，由余弦定理可得，所以，因此，在中，，所以直线与平面所成角的正弦值为考点：直线与平面平行和垂直、平面与平面垂直、直线与平面所成角30．（2015·广东·高考真题）如图，三角形△PDC所在的平面与长方形ABCD所在的平面垂直，PD＝PC

＝4，AB＝6，BC＝3，点E是CD的中点，点F、G分别在线段AB、BC上，且AF＝2FB，CG＝2GB．（1）证明：PE⊥FG；（2）求二面角P﹣AD﹣C的正切值；（3）求直线PA与直线FG所成角的余弦值．【答案】（1）见解析；（2）73；（3）9525．【

分析】（1）通过△PDC为等腰三角形可得PE⊥CD，利用线面垂直判定定理及性质定理即得结论；（2）通过（1）及面面垂直定理可得PG⊥AD，则∠PDC为二面角P﹣AD﹣C的平面角，利用勾股定理即得结论；（3）连结AC，利用勾股定理及已知条件可得FG∥AC，在△P

AC中，利用余弦定理即得直线PA与直线FG所成角的余弦值．【详解】（1）证明：在△PDC中PO＝PC且E为CD中点，∴PE⊥CD，又∵平面PDC⊥平面ABCD，平面PDC∩平面ABCD＝CD，PE⊂平面

PCD，∴PE⊥平面ABCD，又∵FG⊂平面ABCD，∴PE⊥FG；（2）解：由（1）知PE⊥平面ABCD，∴PE⊥AD，又∵CD⊥AD且PE∩CD＝E，∴AD⊥平面PDC，又∵PD⊂平面PDC，∴AD⊥PD，又∵AD⊥CD，∴∠PDC为二面角P﹣AD﹣C的平

面角，在Rt△PDE中，由勾股定理可得：PE2222437PDDE=−=−=，∴tan∠PDC73PGDG==；（3）解：连结AC，则AC2263=+=35，在Rt△ADP中，AP222234ADDP=+=+=5，

∵AF＝2FB，CG＝2GB，∴FG∥AC，∴直线PA与直线FG所成角即为直线PA与直线AC所成角∠PAC，在△PAC中，由余弦定理得cos∠PAC2222PAACPCPAAC+−=2225(35)42535+−=9525=．【点睛】本题考查线线垂直的判定、

二面角及线线角的三角函数值，涉及到勾股定理、余弦定理等知识，注意解题方法的积累，属于中档题．31．（2015·浙江·高考真题）如图，在三棱锥111ABCABC−中，11BAC90ABAC2,4,AAA====，在底面ABC的射影为BC的中点，D为11

BC的中点.（1）证明：11DABCA⊥平面；（2）求直线1AB和平面11BCBC所成的角的正弦值.【答案】（1）见解析；（2）78【详解】（1）利用线面垂直的定义得到线线垂直，根据线面垂直的判定证明直线与平面

垂直；（2）通过添加辅助线，证明1AF⊥平面11BBCC，以此找到直线与平面所成角的平面角1ABF，在直角三角形1ABF中通过确定边长，计算1ABF的正弦值.试题解析：（1）设为C中点，由题意得1AE⊥平面C，所以1AEAE⊥.因为

ABAC=，所以AEBC⊥.所以⊥AE平面1ABC.由D，分别为11,BCBC的中点，得1//DEBB且1DEBB=，从而1//DEAA且1DEAA=，所以1AADE是平行四边形，所以1//ADAE.因为⊥AE平面1ABC，所以1AD⊥平面1A

BC.（2）作1AFDE⊥，垂足为F，连结F.因为⊥AE平面1ABC，所以1BCAE⊥.因为BCAE⊥，所以BC⊥平面1AADE.所以11,BCAFAF⊥⊥平面11BBCC.所以1ABF为直线1AB与平面11BBCC所成角的平面

角.由2,90ABACCAB===，得2EAEB==.由⊥AE平面1ABC，得1114,14AAABAE===.由1114,2,90DEBBDAEADAE=====，得172AF=.所以17sin8ABF=考点：1.空间直线、平面垂直关系的证明；2.直线与平面所成的角.32．（2015·天津

·高考真题）如图,已知1AA⊥平面ABC,AB=AC=3,,,点E,F分别是BC,11AB的中点.（Ⅰ）求证:EF∥平面;（Ⅱ）求证:平面平面1BCB.（Ⅲ）求直线与平面1BCB所成角的大小.【答案】（Ⅰ

）见试题解析;（Ⅱ）见试题解析;（Ⅲ）30.【详解】（Ⅰ）要证明EF∥平面11ABBA,只需证明11ABN且EF平面11ABBA;（Ⅱ）要证明平面11ABN平面1BCB,可证明AEBC⊥,1BB

AE^;（Ⅲ）取1AN中点N,连接11AB,则1AEA^就是直线11AB与平面1BCB所成角,Rt△1ABC中,由11111sin,2ANABNAB==得直线11AB与平面1BCB所成角为30.试题解析:（Ⅰ）证明:如图,连接1AC,在△1BCB中,因为E和F分别是BC,

1BB的中点,所以11ABN,又因为EF平面11ABBA,所以EF∥平面11ABBA.（Ⅱ）因为AB=AC,E为BC中点,所以AEBC⊥,因为1AN⊥平面ABC,所以1AN⊥平面ABC,从而1BBAE^,又1130ABN=,所以⊥AE平

面1BCB,又因为⊥AE平面1BCB,所以平面11ABN平面1BCB.（Ⅲ）取1BC中点M和1AN中点N,连接1NEAA=,11AB因为N和E分别为1AN,BC中点,所以,,故,1ABBB⊥,所以,1

ANAE=,又因为⊥AE平面1BCB,所以11AMB平面1BCB,从而1AEA^就是直线11AB与平面1BCB所成角,在△中,可得AE=2,所以1ANAE==2,因为,所以又由,有,在Rt△中,可得,在Rt△1ABC中,11111sin,2ANABNAB==因此,所以,直线

11AB与平面1BCB所成角为30.考点：本题主要考查空间中线面位置关系的证明,直线与平面所成的角等基础知识,考查空间想象能力及推理论证能力.33．（2015·上海·高考真题）如图，在长方体1111CDCD−中，11=，D2==，、F分别是、C的中点

．证明1、1C、F、四点共面，并求直线1CD与平面11CF所成的角的大小.【答案】【详解】解：如图，以为原点建立空间直角坐标系，可得有关点的坐标为()12,0,1、()1C0,2,1、()2,1,0、()F1,2,0、()C0,2,0、()1D0,

0,1．因为()11C2,2,0=−，()F1,1,0=−，所以11C//F，因此直线11C与F共面，即1、1C、F、共面．设平面的法向量为(,,)nuyw=，则Fn⊥，1FCn⊥，又()F1,1,0=−，()1FC1,0,1=−，故0{0uvuw−+=−+=，

解得uvw==．取1u=，得平面11CF的一个法向量．又()1CD0,2,1=−，故11CD1515CDnn=−．因此直线与平面所成的角的大小为．考点：空间向量求线面角34．（2015·全国·高考真题）如图，长方体1111ABCDABCD−中,

=16AB，=10BC，18AA=，点E，F分别在11AB，11CD上，114AEDF==．过点E，F的平面与此长方体的面相交，交线围成一个正方形．（Ⅰ）在图中画出这个正方形（不必说出画法和理由）；

（Ⅱ）求直线AF与平面所成角的正弦值．【答案】（Ⅰ）详见解析；（Ⅱ）4515．【详解】（Ⅰ）交线围成的正方形EHGF如图：（Ⅱ）作EMAB⊥，垂足为M，则14AMAE==，18EMAA==，因为EHGF为正方形，所以10EHEFBC===．于是226MHEHEM=−=，所以10AH=．以D为

坐标原点，DA的方向为x轴的正方向，建立如图所示的空间直角坐标系Dxyz−，则(10,0,0)A，(10,10,0)H，(10,4,8)E，(0,4,8)F，(10,0,0)FE=，(0,6,8)HE=−．设(,,)nxyz=是平面EHGF的法向量，则0,{0,nFEnHE==即所

以可取(0,4,3)n=．又(10,4,8)AF=−，故45cos,15nAFnAFnAF==．所以直线AF与平面所成角的正弦值为4515．考点：1、直线和平面平行的性质；2、直线和平面所成的角．考点07求二面角及最值或范围1．（2024

·全国新Ⅱ卷·高考真题）如图，平面四边形ABCD中，8AB=，3CD=，53AD=，90ADC=，30BAD=，点E，F满足25AEAD=，12AFAB=，将AEF△沿EF翻折至PEF!，使得43PC=．(1)证明：EFPD⊥；(2)求

平面PCD与平面PBF所成的二面角的正弦值．【答案】(1)证明见解析(2)86565【分析】（1）由题意，根据余弦定理求得2EF=，利用勾股定理的逆定理可证得EFAD⊥，则,EFPEEFDE⊥⊥，结合线面

垂直的判定定理与性质即可证明；（2）由（1），根据线面垂直的判定定理与性质可证明PEED⊥，建立如图空间直角坐标系Exyz−，利用空间向量法求解面面角即可.【详解】（1）由218,53,,52ABADAEADAFAB====，得23,4AEAF==，又30BAD=，在AEF△中，由余

弦定理得2232cos1612242322EFAEAFAEAFBAD=+−=+−=,所以222AEEFAF+=，则AEEF⊥，即EFAD⊥，所以,EFPEEFDE⊥⊥，又,PEDEEPEDE=、平面PDE，

所以EF⊥平面PDE，又PD平面PDE，故EF⊥PD；（2）连接CE，由90,33,3ADCEDCD===，则22236CEEDCD=+=，在PEC中，43,23,6PCPEEC===，得222ECPEPC+=，所以PEE

C⊥，由（1）知PEEF⊥，又,ECEFEECEF=、平面ABCD，所以PE⊥平面ABCD，又ED平面ABCD，所以PEED⊥，则,,PEEFED两两垂直，建立如图空间直角坐标系Exyz−，则(0,0,0),(0,0,23),(0,33,0),(3,33,0),(2,0,0),(0,

23,0)EPDCFA−，由F是AB的中点，得(4,23,0)B，所以(3,33,23),(0,33,23),(4,23,23),(2,0,23)PCPDPBPF=−=−=−=−，设平面PCD和平面PBF的一个法向量分别为1

11222(,,),(,,)nxyzmxyz==，则1111133323033230nPCxyznPDyz=+−==−=，222224232302230mPBxyzmPFxz=+−==−=，令122,3yx==，得11220,3,1,1xzyz==

=−=，所以(0,2,3),(3,1,1)nm==−，所以165cos,65513mnmnmn===，设平面PCD和平面PBF所成角为，则2865sin1cos65=−=，即平面PCD和平面PBF所成角的正弦值为86565.2．（202

4·全国甲卷·高考真题）如图，在以A，B，C，D，E，F为顶点的五面体中，四边形ABCD与四边形ADEF均为等腰梯形，//,//EFADBCAD，4,2ADABBCEF====，10,23EDFB==，M为AD的中点．(1)证明：//BM平面

CDE；(2)求二面角FBME−−的正弦值．【答案】(1)证明见详解；(2)4313【分析】（1）结合已知易证四边形BCDM为平行四边形，可证//BMCD，进而得证；（2）作BOAD⊥交AD于O，连接OF，易证,,OBO

DOF三垂直，采用建系法结合二面角夹角余弦公式即可求解.【详解】（1）因为//,2,4,BCADEFADM==为AD的中点，所以//,BCMDBCMD=，四边形BCDM为平行四边形，所以//BMCD，又因为B

M平面CDE，CD平面CDE，所以//BM平面CDE；（2）如图所示，作BOAD⊥交AD于O，连接OF，因为四边形ABCD为等腰梯形，//,4,BCADAD=2ABBC==，所以2CD=，结合（1）BCD

M为平行四边形，可得2BMCD==，又2AM=，所以ABM为等边三角形，O为AM中点，所以3OB=，又因为四边形ADEF为等腰梯形，M为AD中点，所以,//EFMDEFMD=，四边形EFMD为平行四边形，FMEDAF==，所以AFM△为等腰三

角形，ABM与AFM△底边上中点O重合，OFAM⊥，223OFAFAO=−=，因为222OBOFBF+=，所以OBOF⊥，所以,,OBODOF互相垂直，以OB方向为x轴，OD方向为y轴，OF方向为z轴，建立Oxyz−空间直角坐标系，()0,0,3F，()()()3,0,0,0,1,0,0,2,3B

ME，()()3,1,0,3,0,3BMBF=−=−，()3,2,3BE=−，设平面BFM的法向量为()111,,mxyz=，平面EMB的法向量为()222,,nxyz=，则00mBMmBF==，即1111

30330xyxz−+=−+=，令13x=，得113,1yz==，即()3,3,1m=，则00nBMnBE==，即22222303230xyxyz−+=−++=，令23x=，得223,1yz==−，即()3,3,1n=−，1111cos,

131313mnmnmn===，则43sin,13mn=，故二面角FBME−−的正弦值为4313.3．（2024·北京·高考真题）如图，在四棱锥PABCD−中，//BCAD，1ABBC==，3AD=,点E

在AD上，且PEAD⊥，2PEDE==．(1)若F为线段PE中点，求证：//BF平面PCD．(2)若AB⊥平面PAD，求平面PAB与平面PCD夹角的余弦值．【答案】(1)证明见解析(2)3030【分析】（1）取PD的中点为S，接,S

FSC，可证四边形SFBC为平行四边形，由线面平行的判定定理可得//BF平面PCD.（2）建立如图所示的空间直角坐标系，求出平面APB和平面PCD的法向量后可求夹角的余弦值.【详解】（1）取PD的中点为S，接,SFSC，则1//,12SFED

SFED==，而//,2EDBCEDBC=，故//,SFBCSFBC=，故四边形SFBC为平行四边形，故//BFSC，而BF平面PCD，SC平面PCD，所以//BF平面PCD.（2）因为2ED=，故1AE=，故//,=AEBCAEBC，故四边形AECB为平行四边形，故//CEAB，所以CE

⊥平面PAD，而,PEED平面PAD，故,CEPECEED⊥⊥，而PEED⊥，故建立如图所示的空间直角坐标系，则()()()()()0,1,0,1,1,0,1,0,0,0,2,0,0,0,2ABCDP−−，则()()()()0,1,2,

1,1,2,1,0,2,0,2,2,PAPBPCPD=−−=−−=−=−设平面PAB的法向量为(),,mxyz=，则由00mPAmPB==可得2020yzxyz−−=−−=，取()0,2,1m=−，设平面PCD的法向量为(),,nabc=，则由00nPCnPD

==可得20220abbc−=−=，取()2,1,1n=，故130cos,3056mn−==−，故平面PAB与平面PCD夹角的余弦值为30304．（2024·天津·高考真题）已知四棱柱1111ABCDABCD−中，底面ABCD为梯形，//ABCD，1AA⊥平面ABC

D，ADAB⊥，其中12,1ABAAADDC====．N是11BC的中点，M是1DD的中点．(1)求证1//DN平面1CBM；(2)求平面1CBM与平面11BBCC的夹角余弦值；(3)求点B到平面1CBM的距离

．【答案】(1)证明见解析(2)22211(3)21111【分析】（1）取1CB中点P，连接NP，MP，借助中位线的性质与平行四边形性质定理可得1N//DMP，结合线面平行判定定理即可得证；（2）建立适当空间

直角坐标系，计算两平面的空间向量，再利用空间向量夹角公式计算即可得解；（3）借助空间中点到平面的距离公式计算即可得解.【详解】（1）取1CB中点P，连接NP，MP，由N是11BC的中点，故1//NPCC，且112NPCC=，由M是1DD的中点，故1111122DMDDC

C==，且11//DMCC，则有1//DMNP、1DMNP=，故四边形1DMPN是平行四边形，故1//DNMP，又MP平面1CBM，1DN平面1CBM，故1//DN平面1CBM；（2）以A为原点建

立如图所示空间直角坐标系，有()0,0,0A、()2,0,0B、()12,0,2B、()0,1,1M、()1,1,0C、()11,1,2C，则有()11,1,2CB=−、()1,0,1CM=−、()10

,0,2BB=，设平面1CBM与平面11BBCC的法向量分别为()111,,mxyz=、()222,,nxyz=，则有111111200mCBxyzmCMxz=−+==−+=，12221

22020nCBxyznBBz=−+===，分别取121xx==，则有13y=、11z=、21y=，20z=，即()1,3,1m=、()1,1,0n=，则13222cos,1119111mnmnmn+===+++，故平面1CBM与平面11BBCC的夹

角余弦值为22211；（3）由()10,0,2BB=，平面1CBM的法向量为()1,3,1m=，则有1221111191BBmm==++，即点B到平面1CBM的距离为21111.5．（2023·全国新Ⅱ卷·高考真题）如图，三棱锥ABCD−中，DADBDC==，BDCD⊥，60A

DBADC==，E为BC的中点．(1)证明：BCDA⊥；(2)点F满足EFDA=，求二面角DABF−−的正弦值．【答案】(1)证明见解析；(2)33．【分析】（1）根据题意易证BC⊥平面ADE，从而证得B

CDA⊥；（2）由题可证⊥AE平面BCD，所以以点E为原点，,,EDEBEA所在直线分别为,,xyz轴，建立空间直角坐标系，再求出平面,ABDABF的一个法向量，根据二面角的向量公式以及同角三角函数关系即可解出．【详解】（1）连接,AEDE，因为E为BC中点，DBDC=，所以D

EBC⊥①，因为DADBDC==，60ADBADC==，所以ACD与ABD△均为等边三角形，ACAB=，从而AEBC⊥②，由①②，AEDEE=，,AEDE平面ADE，所以，BC⊥平面ADE，而AD平面ADE，所以BCDA⊥．（2）不

妨设2DADBDC===，BDCD⊥，22,2BCDEAE===．2224AEDEAD+==，AEDE⊥，又,AEBCDEBCE⊥=，,DEBC平面BCDAE⊥平面BCD．以点E为原点，,,EDEBEA所在直线分别为,,xyz轴，

建立空间直角坐标系，如图所示：设(2,0,0),(0,0,2),(0,2,0),(0,0,0)DABE，设平面DAB与平面ABF的一个法向量分别为()()11112222,,,,,nxyznxyz==，二面角DABF−−平面角为,而(

)0,2,2AB=−，因为()2,0,2EFDA==−，所以()2,0,2F−，即有()2,0,0AF=−，1111220220xzyz−+=−=，取11x=，所以1(1,1,1)n=；22222020

yzx−=−=，取21y=，所以2(0,1,1)n=，所以，121226cos332nnnn===，从而63sin193=−=．所以二面角DABF−−的正弦值为33．6．（2023·全国乙卷·高考真题）如图，在三棱锥−PABC中，ABBC⊥，2AB=

，22BC=，6PBPC==，BP，AP，BC的中点分别为D，E，O，5ADDO=，点F在AC上，BFAO⊥.(1)证明：//EF平面ADO；(2)证明：平面ADO⊥平面BEF；(3)求二面角DAOC−−的正弦值.【答案】

(1)证明见解析；(2)证明见解析；(3)22.【分析】（1）根据给定条件，证明四边形ODEF为平行四边形，再利用线面平行的判定推理作答.（2）法一：由（1）的信息，结合勾股定理的逆定理及线面垂直、面面垂直的判定推理作答.法二：过点B作z轴⊥平面BAC，建立如图所示的空间直角

坐标系，设(),,Pxyz，所以由1466PAPBPC===求出P点坐标，再求出平面ADO与平面BEF的法向量12,nn，由120nn=即可证明；（3）法一：由（2）的信息作出并证明二面角的平面角，再结合三角形重心及余弦定理求解作答.法二：求出平面ADO与平面ACO

的法向量，由二面角的向量公式求解即可.【详解】（1）连接,DEOF，设AFtAC=，则(1)BFBAAFtBAtBC=+=−+，12AOBABC=−+，BFAO⊥，则2211[(1)]()(1)4(1)4022BFAOtBAtBCBABCtBAtBCtt=−+−+=−+=−

+=，解得12t=，则F为AC的中点，由,,,DEOF分别为,,,PBPABCAC的中点，于是11//,,//,22DEABDEABOFABOFAB==，即,//DEOFDEOF=，则四边形ODEF为平行四边形

，//,EFDOEFDO=，又EF平面,ADODO平面ADO，所以//EF平面ADO.（2）法一：由（1）可知//EFOD，则66,2AODO==，得3052ADDO==，因此222152ODAOAD+==，则ODAO⊥，有EFAO⊥，又,AOBFBFEFF⊥=，,BFEF平面BE

F，则有AO⊥平面BEF，又AO平面ADO，所以平面ADO⊥平面BEF.法二：因为ABBC⊥，过点B作z轴⊥平面BAC，建立如图所示的空间直角坐标系，()()()2,0,0,,0,0,0,0,22,0ABC，在BDA

△中，2223154122cos266222DBABDAPBADBAB+−+−===−，在PBA△中，22212cos64262146PAPBABPBABPBA=+−=+−−=，设(),,Pxyz，所以由1466PAPBPC==

=可得：()()2222222222146226xyzxyzxyz−++=++=+−+=，可得：1,2,3xyz=−==，所以()1,2,3P−，则123,,222D−，所以123,,222

E，()1,2,0F，()5232,2,0,,,222AOAD=−=−设平面ADO的法向量为()1111,,nxyz=，则1100nAOnAD==，得111112205230222xyxyz−+=−++=，令11x=，则112,3yz==，

所以()11,2,3n=，()123,,,1,2,0222BEBF==设平面BEF的法向量为()2222,,nxyz=，则2200nBEnBF==，得22222123022220xyzxy++=+=，令22x=，则222,0yz=−=，所以(

)22,2,0n=−，()12212200nn=+−+=，所以平面ADO⊥平面BEF；（3）法一：过点O作//OHBF交AC于点H，设ADBEG=，由AOBF⊥，得HOAO⊥，且13FHAH=，又由（2）知，ODAO⊥，则DOH为二面角DAOC−−的平面角，因为,DE

分别为,PBPA的中点，因此G为PAB的重心，即有11,33DGADGEBE==，又13FHAH=，即有32DHGF=，231544622cos6226222PAABD+−+−==，解得14PA=，同理得62BE=，于是2223BEE

FBF+==，即有BEEF⊥，则22216653223GF=+=，从而153GF=，31515232DH==，在DOH△中，13615,,2222OHBFODDH====，于是63152444cos263222DOH+−=

=−，222sin122DOH=−−=，所以二面角DAOC−−的正弦值为22.法二：平面ADO的法向量为()11,2,3n=，平面ACO的法向量为()30,0,1n=，所以13131332c

os,2123nnnnnn===++，因为13,0,πnn，所以213132sin,1cos,2nnnn=−=，故二面角DAOC−−的正弦值为22.7．（2023·北京·高考真题）如图，在三棱锥−PABC中，PA⊥平面ABC

，13PAABBCPC====，．(1)求证：BC⊥平面PAB；(2)求二面角APCB−−的大小．【答案】(1)证明见解析(2)π3【分析】（1）先由线面垂直的性质证得PABC⊥，再利用勾股定理证得BCPB⊥，从而利用线面垂直的判定定理即可得证；（2）结合（

1）中结论，建立空间直角坐标系，分别求得平面PAC与平面PBC的法向量，再利用空间向量夹角余弦的坐标表示即可得解.【详解】（1）因为PA⊥平面,ABCBC平面ABC，所以PABC⊥，同理PAAB⊥，所以PAB为直角

三角形，又因为222PBPAAB=+=，1,3BCPC==，所以222PBBCPC+=，则PBC为直角三角形，故BCPB⊥，又因为BCPA⊥，PAPBP=，所以BC⊥平面PAB.（2）由（1）BC⊥平面PAB，又AB平面PAB，则BC

AB⊥，以A为原点，AB为x轴，过A且与BC平行的直线为y轴，AP为z轴，建立空间直角坐标系，如图，则(0,0,0),(0,0,1),(1,1,0),(1,0,0)APCB，所以(0,0,1),(1,1,0),(0,1,0),(1,1,1)A

PACBCPC====−，设平面PAC的法向量为()111,,mxyz=，则00mAPmAC==，即1110,0,zxy=+=令11x=，则11y=−，所以(1,1,0)m=−，设平面PBC的法向量为()222,,xnyz=，则00nBCnPC

==，即222200yxyz=+−=，令21x=，则21z=，所以(1,0,1)n=，所以11cos,222mnmnmn===，又因为二面角APCB−−为锐二面角，所以二面角APCB−−的大小为π3.8．（2023·天津·高考真题）如图，在三棱

台111ABCABC-中，1AA⊥平面111,,2,1ABCABACABACAAAC⊥====，M为BC中点.，N为AB的中点，(1)求证：1AN//平面1AMC；(2)求平面1AMC与平面11ACCA所成夹角的余弦值；(3)求点C到平面1AMC的距

离．【答案】(1)证明见解析(2)23(3)43【分析】（1）先证明四边形11MNAC是平行四边形，然后用线面平行的判定解决；（2）利用二面角的定义，作出二面角的平面角后进行求解；（3）方法一是利用线面垂直的关系，找到垂线段的长，方法二无需找垂线

段长，直接利用等体积法求解【详解】（1）连接1,MNCA.由,MN分别是,BCBA的中点，根据中位线性质，MN//AC，且12ACMN==，由棱台性质，11AC//AC，于是MN//11AC，由111MNAC==可知，四边形11MNAC是平行四边形，则1AN//1MC，又1AN平面

1CMA，1MC平面1CMA，于是1AN//平面1AMC.（2）过M作MEAC⊥，垂足为E，过E作1EFAC⊥，垂足为F,连接1,MFCE.由ME面ABC，1AA⊥面ABC，故1AAME⊥，又MEAC⊥，1ACAAA=∩，1,ACAA平面11ACCA

，则ME⊥平面11ACCA.由1AC平面11ACCA，故1MEAC⊥，又1EFAC⊥，MEEFE=，,MEEF平面MEF，于是1AC⊥平面MEF，由MF平面MEF，故1ACMF⊥.于是平面1AMC与平面1

1ACCA所成角即MFE.又12ABME==，11cos5CAC=，则12sin5CAC=，故121sin5EFCAC==，在RtMEF中，90MEF=，则43155MF=+=，于是2cos3EFMFEMF==（3）[方法一：几何法]过1

C作1CPAC⊥，垂足为P，作1CQAM⊥，垂足为Q，连接,PQPM，过P作1PRCQ⊥，垂足为R.由题干数据可得，115CACC==，22115CMCPPM=+=，根据勾股定理，21232522CQ=−

=，由1CP⊥平面AMC，AM平面AMC，则1CPAM⊥，又1CQAM⊥，111CQCPC=，11,CQCP平面1CPQ，于是AM⊥平面1CPQ.又PR平面1CPQ，则PRAM⊥，又1PRCQ⊥，1CQAMQ=，1,CQAM平面1CMA，故PR⊥平面1CMA.在1RtCPQ

中，1122223322PCPQPRQC===，又2CAPA=，故点C到平面1CMA的距离是P到平面1CMA的距离的两倍，即点C到平面1AMC的距离是43.[方法二：等体积法]辅助线同方法一.设点C到平面1AM

C的距离为h.()1211112223323CAMCAMCVCPS−===，1111132233222CCMAAMChVhSh−===.由11223CAMCCCMAhVV−−==，即

43h=.9．（2022·全国新Ⅰ卷·高考真题）如图，直三棱柱111ABCABC-的体积为4，1ABC的面积为22．(1)求A到平面1ABC的距离；(2)设D为1AC的中点，1AAAB=，平面1ABC⊥平面11ABBA，求二面角ABDC−−的正弦值．

【答案】(1)2(2)32【分析】（1）由等体积法运算即可得解；（2）由面面垂直的性质及判定可得BC⊥平面11ABBA，建立空间直角坐标系，利用空间向量法即可得解.【详解】（1）在直三棱柱111ABCABC-

中，设点A到平面1ABC的距离为h，则111111112211433333AABCAAABCAABCABBCCCBVShhVSAAV−−−======，解得2h=，所以点A到平面1ABC的距离为2；（2）取1AB的中点E,连接AE,如图，因为1AAAB=，所

以1AEAB⊥,又平面1ABC⊥平面11ABBA，平面1ABC平面111ABBAAB=，且AE平面11ABBA，所以⊥AE平面1ABC，在直三棱柱111ABCABC-中，1BB⊥平面ABC，由BC平面1ABC，BC平面ABC可得AEBC⊥，1BBBC⊥，又1,AEBB平面11AB

BA且相交，所以BC⊥平面11ABBA，所以1,,BCBABB两两垂直，以B为原点，建立空间直角坐标系，如图，由（1）得2AE=，所以12AAAB==，122AB=，所以2BC=，则()()()()10,2,0,0,2,2,0,0,0,2,0,0AABC,所以

1AC的中点()1,1,1D，则()1,1,1BD=，()()0,2,0,2,0,0BABC==,设平面ABD的一个法向量(),,mxyz=，则020mBDxyzmBAy=++===，可取()1,0,1m=−，设平面BDC的一个法向量(),,nabc=，则020nBDabcnBCa

=++===，可取()0,1,1n=−r，则11cos,222mnmnmn===，所以二面角ABDC−−的正弦值为213122−=.10．（2022·全国新Ⅱ卷·高考真题）如图，PO是三棱锥−PABC的高，PAPB=，ABAC

⊥，E是PB的中点．(1)证明：//OE平面PAC；(2)若30ABOCBO==，3PO=，5PA=，求二面角CAEB−−的正弦值．【答案】(1)证明见解析(2)1113【分析】（1）连接BO并延长交AC于点D，连接O

A、PD，根据三角形全等得到OAOB=，再根据直角三角形的性质得到AODO=，即可得到O为BD的中点从而得到//OEPD，即可得证；（2）建立适当的空间直角坐标系，利用空间向量法求出二面角的余弦的绝对值，再根据同角三角函数的基本关系计算可得.【详解】（1

）证明：连接BO并延长交AC于点D，连接OA、PD，因为PO是三棱锥−PABC的高，所以PO⊥平面ABC，,AOBO平面ABC，所以POAO⊥、POBO⊥，又PAPB=，所以POAPOB△△，即OAOB=，所以OABOBA=

，又ABAC⊥，即90BAC=，所以90OABOAD+=，90OBAODA+=，所以ODAOAD=所以AODO=，即AODOOB==，所以O为BD的中点，又E为PB的中点，所以//OEPD，又OE平面PAC，PD平面PAC，所以//O

E平面PAC（2）解：过点A作//AzOP，如图建立空间直角坐标系，因为3PO=，5AP=，所以224OAAPPO=−=，又30OBAOBC==，所以28BDOA==，则4=AD，43AB=，所以12AC=，所以()23,2,0O，()43,0,0B，()23,2,3P，()0

,12,0C，所以333,1,2E，则333,1,2AE=，()43,0,0AB=，()0,12,0AC=，设平面AEB的法向量为(),,nxyz=，则33302430nAExyznABx=++===，令2z

=，则=3y−，0x=，所以()0,3,2n=−；设平面AEC的法向量为(),,mabc=，则33302120mAEabcmACb=++===，令3a=，则6c=−，0b=，所以()3,0,6m=−；所以1243cos,131339nmnmnm−

===−.设二面角CAEB−−的大小为，则43coscos,=13nm=，所以211sin1cos13=−=，即二面角CAEB−−的正弦值为1113.11．（2022·天津·高考真题）直三棱柱111ABCABC-中，112,,AAABACAAABACAB===⊥⊥，D为11AB的中点，E

为1AA的中点，F为CD的中点．(1)求证：//EF平面ABC；(2)求直线BE与平面1CCD所成角的正弦值；(3)求平面1ACD与平面1CCD夹角的余弦值．【答案】(1)证明见解析(2)45(3)10

10【分析】（1）以点1A为坐标原点，1AA、11AB、11AC所在直线分别为x、y、z轴建立空间直角坐标系，利用空间向量法可证得结论成立；（2）利用空间向量法可求得直线BE与平面1CCD夹角的正弦值；（3）利用空间向量法可求得平面1ACD

与平面1CCD夹角的余弦值.【详解】（1）证明：在直三棱柱111ABCABC-中，1AA⊥平面111ABC，且ACAB⊥，则1111ACAB⊥以点1A为坐标原点，1AA、11AB、11AC所在直线分别为x、y、z轴建立如下图所示的空间直角坐标系，则()2,0,0A、()2,2,0B、()2,0

,2C、()10,0,0A、()10,2,0B、()10,0,2C、()0,1,0D、()1,0,0E、11,,12F，则10,,12EF=，易知平面ABC的一个法向量为()1,0,0m=，则0EF

m=，故EFm⊥，EF平面ABC，故//EF平面ABC.（2）解：()12,0,0CC=，()10,1,2CD=−，()1,2,0EB=，设平面1CCD的法向量为()111,,uxyz=，则111112020uCCxuCDyz===−=，取12y=，可

得()0,2,1u=，4cos,5EBuEBuEBu==.因此，直线BE与平面1CCD夹角的正弦值为45.（3）解：()12,0,2AC=，()10,1,0AD=，设平面1ACD的法向量为()222,,vxyz=，则122122200vACxzvADy=+

===，取21x=，可得()1,0,1v=−，则110cos,1052uvuvuv==−=−，因此，平面1ACD与平面1CCD夹角的余弦值为1010.12．（2021·全国新Ⅱ卷·高考真题）在

四棱锥QABCD−中，底面ABCD是正方形，若2,5,3ADQDQAQC====．（1）证明：平面QAD⊥平面ABCD；（2）求二面角BQDA−−的平面角的余弦值．【答案】（1）证明见解析；（2）23.【分析】（

1）取AD的中点为O，连接,QOCO，可证QO⊥平面ABCD，从而得到面QAD⊥面ABCD.（2）在平面ABCD内，过O作//OTCD，交BC于T，则OTAD⊥，建如图所示的空间坐标系，求出平面QAD、平面BQD的法向量后可求二面角的余弦值.【详解】（1）取AD的中点为O，连接,QO

CO.因为QAQD=，OAOD=，则QO⊥AD，而2,5ADQA==，故512QO=−=.在正方形ABCD中，因为2AD=，故1DO=，故5CO=，因为3QC=，故222QCQOOC=+，故QOC为直角三角形且QOOC⊥，因为OCADO=，故QO⊥平面ABCD，因为QO平面QAD，故平面Q

AD⊥平面ABCD.（2）在平面ABCD内，过O作//OTCD，交BC于T，则OTAD⊥，结合（1）中的QO⊥平面ABCD，故可建如图所示的空间坐标系.则()()()0,1,0,0,0,2,2,1,0DQB−，故()()2,1,2,2,2,0BQBD=−=−.设平面Q

BD的法向量(),,nxyz=，则00nBQnBD==即220220xyzxy−++=−+=，取1x=，则11,2yz==，故11,1,2n=.而平面QAD的法向量为()1,0,0m=，故12cos,3312mn==.二面角BQD

A−−的平面角为锐角，故其余弦值为23.13．（2021·全国甲卷·高考真题）已知直三棱柱111ABCABC-中，侧面11AABB为正方形，2ABBC==，E，F分别为AC和1CC的中点，D为棱11AB上的点．11BFAB⊥（1）证明：BFDE⊥；（2）当1

BD为何值时，面11BBCC与面DFE所成的二面角的正弦值最小?【答案】（1）证明见解析；（2）112BD=【分析】（1）方法二：通过已知条件，确定三条互相垂直的直线，建立合适的空间直角坐标系，借助空间向量证明线线垂直；（

2）方法一：建立空间直角坐标系，利用空间向量求出二面角的平面角的余弦值最大，进而可以确定出答案；【详解】（1）[方法一]：几何法因为1111,//BFABABAB⊥，所以BFAB⊥．又因为1ABBB⊥，1BFBBB=，所以AB⊥平面11BCCB．又因为2ABBC==，构

造正方体1111ABCGABCG−，如图所示，过E作AB的平行线分别与AGBC，交于其中点,MN，连接11,AMBN，因为E，F分别为AC和1CC的中点，所以N是BC的中点，易证1RtRtBCFBBN，则1CBFBBN=．又因

为1190BBNBNB+=，所以1190CBFBNBBFBN+=⊥，．又因为111111,BFABBNABB⊥=，所以BF⊥平面11AMNB．又因为ED平面11AMNB，所以BFDE⊥．[方法二]【最优解】：向量法因为三棱柱111ABC

ABC-是直三棱柱，1BB⊥底面ABC，1BBAB⊥11//ABAB，11BFAB⊥，BFAB⊥，又1BBBFB=，AB⊥平面11BCCB．所以1,,BABCBB两两垂直．以B为坐标原点，分别以1,,BABCBB所在直线为,,xyz轴建立空间直角坐标系，如图

．()()()0,0,0,2,0,0,0,2,0,BAC()()()1110,0,2,2,0,2,0,2,2BAC，()()1,1,0,0,2,1EF．由题设(),0,2Da（02a）．因为()

()0,2,1,1,1,2BFDEa==−−，所以()()0121120BFDEa=−++−=，所以BFDE⊥．[方法三]：因为11BFAB⊥，11//ABAB，所以BFAB⊥，故110BFAB=，0BFAB=，所以()11BFEDBFEBBBBD=

++()11=BFBDBFEBBB++1BFEBBFBB=+11122BFBABCBFBB=−−+11122BFBABFBCBFBB=−−+112BFBCBFBB=−+111coscos2BFBCFBCBFB

BFBB=−+121=52520255−+=，所以BFED⊥．（2）[方法一]【最优解】：向量法设平面DFE的法向量为(),,mxyz=，因为()()1,1,1,1,1,2EFDEa=−=−−，所以00mEFmDE

==，即()0120xyzaxyz−++=−+−=．令2za=−，则()3,1,2maa=+−因为平面11BCCB的法向量为()2,0,0BA=，设平面11BCCB与平面DEF的二面角的平面角为，则cosmBAmBA=262

2214aa=−+232214aa=−+．当12a=时，22214aa−+取最小值为272，此时cos取最大值为363272=．所以()2min63sin133=−=，此时112BD=．[方法二]：几何法如图所示，延长EF交1

1AC的延长线于点S，联结DS交11BC于点T，则平面DFE平面11BBCCFT=．作1BHFT⊥，垂足为H，因为1DB⊥平面11BBCC，联结DH，则1DHB为平面11BBCC与平面DFE所成二面角的平面角．设1,BDt=[0,2],t1BTs=，过1C作111//CGA

B交DS于点G．由111113CSCGSAAD==得11(2)3CGt=−．又1111BDBTCGCT=，即12(2)3tsst=−−，所以31tst=+．又111BHBTCFFT=，即1211(2)BHss=+−，所以121(2)sBHs=+−．所以2211DHBHBD=+22

21(2)sts=++−2229225tttt=+−+．则11sinBDDHBDH=2229225ttttt=+−+219119222t=+−+，所以，当12t=时，()1min3sin3DHB=．[方法三]：投影法如图，联结1,FBFN，DEF在平面11BB

CC的投影为1BNF，记面11BBCC与面DFE所成的二面角的平面角为，则1cosBNFDEFSS=．设1(02)BDtt=，在1RtDBF中，222115DFBDBFt=+=+．在RtECF中，223EFECFC=+=，过D作1

BN的平行线交EN于点Q．在RtDEQ△中，2225(1)DEQDEQt=+=+−．在DEF中，由余弦定理得222cos2DFEFDEDFEDFEF+−=()22315(1)35ttt++=+，()222214sin35ttDFEt−+=+，1sin2DFESDFEFDFE=21221

42tt=−+，13,2BNFS=1cosBNFDFESS=232214tt=−+，()29sin127tt=−−+，当12t=，即112BD=，面11BBCC与面DFE所成的二面角的正弦值最小，最小值为33．【整体点评】第

一问，方法一为常规方法，不过这道题常规方法较为复杂，方法二建立合适的空间直角坐标系，借助空间向量求解是最简单，也是最优解；方法三利用空间向量加减法则及数量积的定义运算进行证明不常用，不过这道题用这种方法过程也很简单，可以开拓学生的思维.第二问：方法一建立空间直角坐标系，利用空间

向量求出二面角的平面角是最常规的方法，也是最优方法；方法二：利用空间线面关系找到，面11BBCC与面DFE所成的二面角，并求出其正弦值的最小值，不是很容易找到；方法三：利用面DFE在面11BBCC上的投影三角形的面积与DFE△面积之比即为面11BBCC与面DFE所成的二面角的余

弦值，求出余弦值的最小值，进而求出二面角的正弦值最小，非常好的方法，开阔学生的思维．14．（2021·全国乙卷·高考真题）如图，四棱锥PABCD−的底面是矩形，PD⊥底面ABCD，1PDDC==，M为BC的中点，且PBAM⊥．（1）求BC；（

2）求二面角APMB−−的正弦值．【答案】（1）2；（2）7014【分析】（1）以点D为坐标原点，DA、DC、DP所在直线分别为x、y、z轴建立空间直角坐标系，设2BCa=，由已知条件得出0PBAM=，求出a的值，即可得出BC的长；（2）求出平面P

AM、PBM的法向量，利用空间向量法结合同角三角函数的基本关系可求得结果.【详解】（1）[方法一]：空间坐标系+空间向量法PD⊥平面ABCD，四边形ABCD为矩形，不妨以点D为坐标原点，DA、DC、DP所在直线分别

为x、y、z轴建立如下图所示的空间直角坐标系Dxyz−，设2BCa=，则()0,0,0D、()0,0,1P、()2,1,0Ba、(),1,0Ma、()2,0,0Aa，则()2,1,1PBa=−，(),1,0

AMa=−，PBAM⊥，则2210PBAMa=−+=，解得22a=，故22BCa==；[方法二]【最优解】：几何法+相似三角形法如图，连结BD．因为PD⊥底面ABCD，且AM底面ABCD，所以PDAM⊥．又因为PBAM⊥，PBPDP=，所以

AM⊥平面PBD．又BD平面PBD，所以AMBD⊥．从而90ADBDAM+=．因为90+=MABDAM，所以=MABADB．所以∽ADBBAM，于是=ADBAABBM．所以2112B

C=．所以2BC=．[方法三]：几何法+三角形面积法如图，联结BD交AM于点N．由[方法二]知⊥AMDB．在矩形ABCD中，有∽DANBMN，所以2==ANDAMNBM，即23ANAM=．令2(0)=BCtt，因为M为BC的中点，则BMt=，241=+DBt，21=+AMt．由11

22==DABSDAABDBAN，得221241123=++ttt，解得212t=，所以22==BCt．（2）[方法一]【最优解】：空间坐标系+空间向量法设平面PAM的法向量为()111,,mxyz=，则2,1,02AM=−，()2,0,1AP=−，由111120

220mAMxymAPxz=−+==−+=，取12x=，可得()2,1,2m=，设平面PBM的法向量为()222,,nxyz=，2,0,02BM=−，()2,1,1BP=−−，由22

2220220nBMxnBPxyz=−==−−+=，取21y=，可得()0,1,1n=，3314cos,1472mnmnmn===，所以，270sin,1cos,14mnmn=−=，因此，二面角

APMB−−的正弦值为7014.[方法二]：构造长方体法+等体积法如图，构造长方体1111ABCDABCD−，联结11,ABAB，交点记为H，由于11ABAB⊥，1ABBC⊥，所以AH⊥平面11ABCD．过H作1DM的垂线，垂足记为G．联结AG，由三垂线定理可知1⊥AGDM，故AGH为二面

角APMB−−的平面角．易证四边形11ABCD是边长为2的正方形，联结1DH，HM．111111111,2DHMDHMDAHHBMMCDABCDSDMHGSSSSS==−−−正方形，由等积法解得31010=HG．在R

tAHG中，2310,210==AHHG，由勾股定理求得355=AG．所以，70sin14AHAGHAG==，即二面角APMB−−的正弦值为7014．【整体点评】（1）方法一利用空坐标系和空间向量的坐标运算求解；方法二利用线面垂直

的判定定理，结合三角形相似进行计算求解，运算简洁，为最优解；方法三主要是在几何证明的基础上，利用三角形等面积方法求得.（2）方法一，利用空间坐标系和空间向量方法计算求解二面角问题是常用的方法，思路清晰，运算简洁，为最优解；方法二采用构造长方体方法+等体积转化法，技巧性较强，需注意进行严格的论证

.15．（2021·天津·高考真题）如图，在棱长为2的正方体1111ABCDABCD−中，E为棱BC的中点，F为棱CD的中点．（I）求证：1//DF平面11AEC；（II）求直线1AC与平面11AEC所成角的正弦值．（III）求二面角1

1AACE−−的正弦值．【答案】（I）证明见解析；（II）39；（III）13.【分析】（I）建立空间直角坐标系，求出1DF及平面11AEC的一个法向量m，证明1mDF⊥，即可得证；（II）求出1AC，由1sincos,AmC=运算即可得解；（III）求得平面11AA

C的一个法向量DB，由cos,DBmDBmDBm=结合同角三角函数的平方关系即可得解.【详解】（I）以A为原点，1,,ABADAA分别为,,xyz轴，建立如图空间直角坐标系，则()0,0,0A,()10,0,2A,()2,0,0B,()2,2,0C,()0,2,0D,()12,2

,2C,()10,2,2D，因为E为棱BC的中点，F为棱CD的中点，所以()2,1,0E，()1,2,0F，所以()11,0,2DF=−,()112,2,0AC=,()12,1,2AE=−,设平面11AEC的一个法向量为()111

,,mxyz=，则11111111202202mxymxyAAEzC+=+−===，令12x=，则()2,2,1m=−，因为1220mDF=−=，所以1mDF⊥，因为1DF平面11AEC，所以1//DF平面11AEC；（II）由（1）得，()12,2,2AC=，设直线1AC与

平面11AEC所成角为，则11123sincos,9323mACACmmCA====；（III）由正方体的特征可得，平面11AAC的一个法向量为()2,2,0DB=−，则822cos,3322DBmDB

mDBm===，所以二面角11AACE−−的正弦值为211cos,3DBm−=.16．（2020·天津·高考真题）如图，在三棱柱111ABCABC-中，1CC⊥平面,,2ABCACBCACBC⊥==，13CC=，点,DE分别在棱

1AA和棱1CC上，且12,ADCEM==为棱11AB的中点．（Ⅰ）求证：11CMBD⊥；（Ⅱ）求二面角1BBED−−的正弦值；（Ⅲ）求直线AB与平面1DBE所成角的正弦值．【答案】（Ⅰ）证明见解析；（Ⅱ）306；（Ⅲ）33.【分析】以C为原点，分别以1,,CACBCC的方向为x轴，y轴，z轴的

正方向建立空间直角坐标系.（Ⅰ）计算出向量1CM和1BD的坐标，得出110CMBD=，即可证明出11CMBD⊥；（Ⅱ）可知平面1BBE的一个法向量为CA，计算出平面1BED的一个法向量为n，利用空间向量法计算出二面角1BBED−−的余弦值，利用

同角三角函数的基本关系可求解结果；（Ⅲ）利用空间向量法可求得直线AB与平面1DBE所成角的正弦值.【详解】依题意，以C为原点，分别以CA、CB、1CC的方向为x轴、y轴、z轴的正方向建立空间直角坐标系（如图），可得()0,0,0C、()2,0,0A

、()0,2,0B、()10,0,3C、()12,0,3A、()10,2,3B、()2,0,1D、()0,0,2E、()1,1,3M.（Ⅰ）依题意，()11,1,0CM=，()12,2,2BD=−−，从而112200CMBD=−+=，所以11CM

BD⊥；（Ⅱ）依题意，()2,0,0CA=是平面1BBE的一个法向量，()10,2,1EB=，()2,0,1ED=−．设(),,nxyz=为平面1DBE的法向量，则100nEBnED==，即2020yzxz+=

−=，不妨设1x=，可得()1,1,2n=−．26cos,626CCAnACnAn===，230sin,1cos,6CAnCAn=−=．所以，二面角1BBED−−的正弦值为306；（Ⅲ）依题意，()2,2,0AB=−．由（Ⅱ）知()1,1,2n=−为平面1DBE的

一个法向量，于是43cos,3226ABnABnABn−===−．所以，直线AB与平面1DBE所成角的正弦值为33.【点睛】本题考查利用空间向量法证明线线垂直，求二面角和线面角的正弦值，考查推理能力与计算能力，属于中档题.1

7．（2020·江苏·高考真题）在三棱锥A—BCD中，已知CB=CD=5,BD=2，O为BD的中点，AO⊥平面BCD，AO=2，E为AC的中点．（1）求直线AB与DE所成角的余弦值；（2）若点F在BC上，满足

BF=14BC，设二面角F—DE—C的大小为θ，求sinθ的值．【答案】（1）1515（2）23913【分析】（1）建立空间直角坐标系，利用向量数量积求直线向量夹角，即得结果；（2）先求两个平面法向量，根据向量数量积求法向量夹角，最后根据二面角与向量夹角关系得结

果.【详解】（1）连,COBCCDBOODCOBD==⊥Q以,,OBOCOA为,,xyz轴建立空间直角坐标系，则(0,0,2),(1,0,0),(0,2,0),(1,0,0)(0,1,1)ABCDE−115(1,0,2

),(1,1,1)cos,1553ABDEABDE−=−===−uuuruuuruuuruuur从而直线AB与DE所成角的余弦值为1515（2）设平面DEC一个法向量为1(,,),nxyz=11200(1,2,0),00xynDCDCxyznDE

+===++==令112,1(2,1,1)yxzn==−==−ur设平面DEF一个法向量为2111(,,),nxyz=uur11221117100171(,,0),4244200xynDFDFDBBFDBBCnDExyz+==

=+=+==++=令111272,5(2,7,5)yxzn=−===−uur1261cos,67813nn−==−uruur因此12239sin1313==【点睛】本题考查利用向量求线线角与二面角，考查基本分析求解能力，属中档题.18．（2020·全国·高

考真题）如图，在长方体1111ABCDABCD−中，点,EF分别在棱11,DDBB上，且12DEED=，12BFFB=．（1）证明：点1C在平面AEF内；（2）若2AB=，1AD=，13AA=，求二面角1AEFA−−的正弦值．【答案】（1）证明见解析；（2）427.【分析】

（1）方法一:连接1CE、1CF，证明出四边形1AECF为平行四边形，进而可证得点1C在平面AEF内；（2）方法一：以点1C为坐标原点，11CD、11CB、1CC所在直线分别为x、y、z轴建立空间直角坐标系1Cxyz−，

利用空间向量法可计算出二面角1AEFA−−的余弦值，进而可求得二面角1AEFA−−的正弦值.【详解】（1）［方法一］【最优解】：利用平面基本事实的推论在棱1CC上取点G，使得112CGCG=，连接DG、FG、1CE、1CF，如图1所示.在长方体1111ABCDABCD−中，//,BFCGBFCG

=，所以四边形BCGF为平行四边形，则//,BCFGBCFG=，而,//BCADBCAD=，所以//,ADFGADFG=，所以四边形DAFG为平行四边形，即有//AFDG，同理可证四边形1DECG为平行四边形，1//CEDG，1//CEAF，因此点1C在平面AEF内.［方法二

］：空间向量共线定理以11111,,CDCBCC分别为x轴，y轴，z轴，建立空间直角坐标系，如图2所示．设11111,,3CDaCBbCCc===，则1(0,0,0),(,0,2),(0,,),(,,3)CEacFbcAabc．所以1(,

0,2),(,0,2)CEacFAac==．故1CEFA=．所以1AFCE∥，点1C在平面AEF内．［方法三］：平面向量基本定理同方法二建系，并得1(0,0,0),(,0,2),(0,,),(,,3)CEacFbcAabc，所以1

11(,0,2),(0,,),(,,3)CEacCFbcCAabc===．故111CACECF=+．所以点1C在平面AEF内．［方法四］：根据题意，如图3，设11111,2,3ADaABbAAc===．在平面11ABBA内，因为12BFFB=，所以111

1133BFBBAA==．延长AF交11AB于G，AF平面AEF，11AB平面1111DCBA．11,GAFGAB，所以G平面,AEFG平面1111DCBA①．延长AE交11AD于H，同理H平面,AEFH平面1111DCBA②．由

①②得，平面AEF平面1111ABCDGH=．连接11,,GHGCHC，根据相似三角形知识可得11,2GBbDHa==．在11RtCBG中，221CGab=+．同理，在11RtCDH中，2212CHab=+．如图4，在1RtAGH中，223GHab=+．所以11GHCGCH=+，即G，1C，H

三点共线．因为GHÌ平面AEF，所以1C平面AEF，得证．［方法五］：如图5，连接11,,DFEBDB，则四边形1DEBF为平行四边形，设1DB与EF相交于点O，则O为1,EFDB的中点．联结1AC，由长方体知识知，体对角线交于一点，且为它们的中点，即11ACBDO=，

则1AC经过点O，故点1C在平面AEF内．（2）［方法一］【最优解】：坐标法以点1C为坐标原点，11CD、11CB、1CC所在直线分别为x、y、z轴建立如下图所示的空间直角坐标系1Cxyz−，如图2.则()2,1

,3A、()12,1,0A、()2,0,2E、()0,1,1F，()0,1,1AE=−−，()2,0,2AF=−−，()10,1,2AE=−，()12,0,1AF=−，设平面AEF的一个法向量为()111,,mxyz=，由00mAEmAF==

，得11110220yzxz−−=−−=取11z=−，得111xy==，则()1,1,1m=−，设平面1AEF的一个法向量为()222,,nxyz=，由1100nAEnAF==，得22222020yzxz−+=−

+=，取22z=，得21x=，24y=，则()1,4,2n=，37cos,7321mnmnmn===，设二面角1AEFA−−的平面角为，则7cos7=，242sin1cos7=−=.因此，二面角1AEFA−−的正弦值为427.［方法二］：定义法在

AEF△中，2,22,516AEAFEF===+=，即222AEEFAF+=，所以AEEF⊥．在1AEF中，115AEAF==，如图6，设,EFAF的中点分别为M，N，连接11,,AMMNAN，则1,AMEFMNEF⊥⊥，所以1AMN为

二面角1AEFA−−的平面角．在1AMN中，22111214,,522MNAMAFMFAN==−==．所以1175722cos7214222AMN+−==−，则1142sin177AMN=−=．［方法三］：向量法由题意得112,8,5,6AEAFAFAEEF====

=，由于222AEEFAF+=，所以AEEF⊥．如图7，在平面1AEF内作1AGEF⊥，垂足为G，则EA与1GA的夹角即为二面角1AEFA−−的大小．由11AAAEEGGA=++，得22221111222AAAEEGGAAEEGEGGAAEGA=++++

+．其中，1614,22EGAG==，解得11AEGA=，11cos,7AEGA=．所以二面角1AEFA−−的正弦值427．［方法四］：三面角公式由题易得，112,22,6,5,5EAFAFEEAFA=====．所以2222221

111(2)(5)310cos210225EAEAAAAEAEAEA+−+−−===．222222(2)(6)(22)cos0,sin12226EAEFAFAEFAEFEAEF+−+−====．22222211111(5)(6)

(5)3070cos,sin21010256EAEFAFAEFAEFEAEF+−+−====．设为二面角1AEFA−−的平面角，由二面角的三个面角公式，得111coscoscos107cossinsin770AEAAEFAEFA

EFAEF−−−===，所以42sin7=．【整体点评】（1）方法一：通过证明直线1//CEAF，根据平面的基本事实二的推论即可证出，思路直接，简单明了，是通性通法，也是最优解；方法二：利用空间向量基本定理证明；方法三：利用平面向量基本定理；方法四：利

用平面的基本事实三通过证明三点共线说明点在平面内；方法五：利用平面的基本事实以及平行四边形的对角线和长方体的体对角线互相平分即可证出．（2）方法一：利用建立空间直角坐标系，由两个平面的法向量的夹角和二面角的关系求

出；方法二：利用二面角的定义结合解三角形求出；方法三：利用和二面角公共棱垂直的两个向量夹角和二面角的关系即可求出，为最优解；方法四：利用三面角的余弦公式即可求出．19．（2020·全国·高考真题）如图，D为圆锥的顶点，O是圆锥底面的圆心，AE为底面直径，AEAD=．ABC是底面的内接正三角形，P

为DO上一点，66PODO=．（1）证明：PA⊥平面PBC；（2）求二面角BPCE−−的余弦值．【答案】（1）证明见解析；（2）255.【分析】（1）要证明PA⊥平面PBC，只需证明PAPB⊥，PAPC⊥即可；（2）方

法一：过O作ON∥BC交AB于点N，以O为坐标原点，OA为x轴，ON为y轴建立如图所示的空间直角坐标系，分别算出平面PCB的一个法向量n，平面PCE的一个法向量为m，利用公式cos,||||nmmnnm=计算即可得到答案.【详解】（1）[方法一

]：勾股运算法证明由题设，知DAE为等边三角形，设1AE=，则32DO=，1122COBOAE===，所以6264PODO==，2264PCPOOCPBPA=+===又ABC为等边三角形，则2sin60BAOA=，所以32BA=，22234PAPBAB+==，则90APB

=，所以PAPB⊥，同理PAPC⊥，又PCPBP=，所以PA⊥平面PBC；[方法二]：空间直角坐标系法不妨设23AB=，则4sin60===ABAEAD，由圆锥性质知DO⊥平面ABC，所以22224223=−=−=DOADAO，所以626==POD

O．因为O是ABC的外心，因此AEBC⊥．在底面过O作BC的平行线与AB的交点为W，以O为原点，OW方向为x轴正方向，OE方向为y轴正方向，OD方向为z轴正方向，建立空间直角坐标系Oxyz−，则(0,2,0)A−，(

3,1,0)B，(3,1,0)C−，(0,2,0)E，(0,0,2)P．所以(0,2,2)AP=，(3,1,2)=−−BP，(3,1,2)=−CP．故0220=−+=APBP，0220=−+=APCP．所以APBP

⊥，APCP⊥．又BPCPP=，故AP⊥平面PBC．[方法三]：因为ABC是底面圆O的内接正三角形，且AE为底面直径，所以AEBC⊥．因为DO（即PO）垂直于底面，BC在底面内，所以POBC⊥．又因为PO平面PAE，AE平面PAE，POAEO=I，所以BC

⊥平面PAE．又因为PA平面PAE，所以PABC⊥．设AEBCF=，则F为BC的中点，连结PF．设DOa=，且66PODO=，则32AFa=，22PAa=，12PFa=．因此222+=PAPFAF，从而PAPF⊥．又因为PFBCF=，所以PA⊥平

面PBC．[方法四]：空间基底向量法如图所示，圆锥底面圆O半径为R，连结DE，AEADDE==，易得3ODR=，因为66=POOD，所以22=POR．以,,OAOBOD为基底，OD⊥平面ABC，则66=+=−+APAOOPOAOD，66=+=

−+BPBOOPOBOD，且212OAOBR=−，0OAODOBOD==所以6666=−+−+=APBPOAODOBOD26610666−−+=OAOBOAODOBODOD．故0APBP=．所以APBP⊥，即APBP⊥．同理APCP

⊥．又BPCPP=，所以AP⊥平面PBC．（2）[方法一]：空间直角坐标系法过O作ON∥BC交AB于点N，因为PO⊥平面ABC，以O为坐标原点，OA为x轴，ON为y轴建立如图所示的空间直角坐标系，则121313(,0,0),(0,0,),(,,0),(,,0)244444EPBC−

−−−，132(,,)444PC=−−−，132(,,)444PB=−−，12(,0,)24PE=−−，设平面PCB的一个法向量为111(,,)nxyz=，由00nPCnPB==，得111111320320xyzxyz−

−−=−+−=，令12x=，得111,0zy=−=，所以(2,0,1)n=−，设平面PCE的一个法向量为222(,,)mxyz=由00mPCmPE==，得22222320220xyzxz−−−=−−=，令21x=，得

2232,3zy=−=，所以3(1,,2)3m=−故2225cos,5||||1033nmmnnm===，设二面角BPCE−−的大小为，由图可知二面角为锐二面角，所以25cos5=.[方法二]【最优解】：

几何法设=BCAEF，易知F是BC的中点，过F作∥FGAP交PE于G，取PC的中点H，联结GH，则∥HFPB．由PA⊥平面PBC，得FG⊥平面PBC．由（1）可得，222BCPBPC=+，得PBPC⊥．所以FHPC⊥，根据三垂线定理，得GHPC⊥．所以GHF是二面角BPCE−

−的平面角．设圆O的半径为r，则3sin602==AFABr，2AEr=，12=EFr，13EFAF=，所以14=FGPA，1122==FHPBPA，12=FGFH．在RtGFH中，1tan2==FGGHFFH，25cos5=GHF．所以二面角BPCE−−的余弦值为255

．[方法三]：射影面积法如图所示，在PE上取点H，使14HEPE=，设BCAEN=，连结NH．由（1）知14NEAE=，所以∥NHPA．故NH⊥平面PBC．所以，点H在面PBC上的射影为N．故由射影面积法可知二面角BPCE

−−的余弦值为cosPCNPCHSθS=．在PCE中，令62==PCPE，则1CE=，易知54=PCES．所以335416PCHPCESS==．又1328PCNPBCSS==，故3258cos53516PCNPCHS

θS===所以二面角BPCE−−的余弦值为255．【整体点评】本题以圆锥为载体，隐含条件是圆锥的轴垂直于底面，（1）方法一：利用勾股数进行运算证明，是在给出数据去证明垂直时的常用方法；方法二：选择建系利用空间向量法，给空间立体感较弱的学生提供了

可行的途径；方法三：利用线面垂直，结合勾股定理可证出；方法四：利用空间基底解决问题，此解法在解答题中用的比较少；（2）方法一：建系利用空间向量法求解二面角，属于解答题中求角的常规方法；方法二：利用几何法

，通过三垂线法作出二面角，求解三角形进行求解二面角，适合立体感强的学生；方法三：利用射影面积法求解二面角，提高解题速度.20．（2019·北京·高考真题）如图，在四棱锥P–ABCD中，PA⊥平面ABCD，AD⊥CD，AD∥BC，PA

=AD=CD=2，BC=3．E为PD的中点，点F在PC上，且13PFPC=．（Ⅰ）求证：CD⊥平面PAD；（Ⅱ）求二面角F–AE–P的余弦值；（Ⅲ）设点G在PB上，且23PGPB=．判断直线AG是否在平面AEF内，说明理由．【答案】

(Ⅰ)见解析；(Ⅱ)33；(Ⅲ)见解析.【分析】(Ⅰ)由题意利用线面垂直的判定定理即可证得题中的结论；(Ⅱ)建立空间直角坐标系，结合两个半平面的法向量即可求得二面角F-AE-P的余弦值；(Ⅲ)首先求得点G的坐标，然后结合平面AEF的法向量和直线AG

的方向向量可判断直线是否在平面内.【详解】(Ⅰ)由于PA⊥平面ABCD，CD平面ABCD，则PA⊥CD，由题意可知AD⊥CD，且PA∩AD=A，由线面垂直的判定定理可得CD⊥平面PAD.(Ⅱ)以点A为坐标原点，平面ABCD内与AD垂直的直线为x轴，AD,AP方

向为y轴，z轴建立如图所示的空间直角坐标系Axyz−，易知：()()()()0,0,0,0,0,2,2,2,0,0,2,0APCD，由13PFPC=可得点F的坐标为224,,333F，由1

2PEPD=可得()0,1,1E，设平面AEF的法向量为：(),,mxyz=，则()()()224224,,,,0333333,,0,1,10mAFxyzxyzmAExyzyz==++===+=，据此可得平面AE

F的一个法向量为：()1,1,1m=−，很明显平面AEP的一个法向量为()1,0,0n=r，13cos,331mnmnmn===，二面角F-AE-P的平面角为锐角，故二面角F-AE-P的余弦值为33.(Ⅲ)易知

()()0,0,2,2,1,0PB−，由23PGPB=可得422,,333G−，则422,,333AG=−，注意到平面AEF的一个法向量为：()1,1,1m=−，其0mAG=且点A在平面AEF内，故直线AG在平面AEF内.2

1．（2019·全国·高考真题）图1是由矩形ADEB，Rt△ABC和菱形BFGC组成的一个平面图形，其中AB=1，BE=BF=2，∠FBC=60°，将其沿AB，BC折起使得BE与BF重合，连结DG，如图2.（1）证明：图2中的

A，C，G，D四点共面，且平面ABC⊥平面BCGE；（2）求图2中的二面角B−CG−A的大小.【答案】(1)见详解；(2)30.【分析】(1)因为折纸和粘合不改变矩形ABED，RtABC和菱形BFGC内部的夹角，所以//ADBE，//BFCG依然成立，又因E

和F粘在一起，所以得证.因为AB是平面BCGE垂线，所以易证.(2)在图中找到BCGA−−对应的平面角，再求此平面角即可.于是考虑B关于GC的垂线，发现此垂足与A的连线也垂直于CG.按照此思路即证.【详解】(1)证：//ADBE，//BFCG，又

因为E和F粘在一起.//ADCG，A，C，G，D四点共面.又,ABBEABBC⊥⊥.AB⊥平面BCGE，AB平面ABC，平面ABC⊥平面BCGE，得证.(2)过B作BHGC⊥延长线于H，连结AH，因为A

B⊥平面BCGE，所以ABGC⊥而又BHGC⊥，故GC⊥平面HAB，所以AHGC⊥.又因为BHGC⊥所以BHA是二面角BCGA−−的平面角，而在BHC△中90BHC=，又因为60FBC=故60BCH=，所以si

n603BHBC==.而在ABH中90ABH=,13tan33ABBHABH===，即二面角BCGA−−的度数为30.【点睛】很新颖的立体几何考题．首先是多面体粘合问题，考查考生在粘合过程中哪些量是不变的．再者粘合后的多面体不是直棱柱，建系的向量

解法在本题中略显麻烦，突出考查几何方法．最后将求二面角转化为求二面角的平面角问题考查考生的空间想象能力．22．（2019·全国·高考真题）如图，长方体ABCD–A1B1C1D1的底面ABCD是正方形，点E在棱AA1上，BE⊥EC1.（1）证明：BE⊥平

面EB1C1；（2）若AE=A1E，求二面角B–EC–C1的正弦值.【答案】（1）证明见解析；（2）32【分析】（1）利用长方体的性质，可以知道11BC⊥侧面11ABBA，利用线面垂直的性质可以证明出11BCEB⊥

，这样可以利用线面垂直的判定定理，证明出BE⊥平面11EBC；（2）以点B坐标原点，以1,,BCBABB分别为,,xyz轴，建立空间直角坐标系，设正方形ABCD的边长为a，1BBb=，求出相应点的坐标，

利用1BEEC⊥，可以求出,ab之间的关系，分别求出平面EBC、平面1ECC的法向量，利用空间向量的数量积公式求出二面角1BECC−−的余弦值的绝对值，最后利用同角的三角函数关系，求出二面角1BECC−−的正弦值.【详解】（1）证明：因为1111ABCDABCD−是长方体，所以11BC⊥侧

面11ABBA，而BE平面11ABBA，所以11BEBC⊥又1BEEC⊥，1111BCECC=，111,BCEC平面11EBC，因此BE⊥平面11EBC；（2）[方法一]【三垂线定理】由（1）知，1BEEB⊥，又E为1AA的中点，

所以1BEB，为等腰直角三角形，所以12AAAB=．如图2，联结AC，与BD相交于点O，因为1AA⊥平面ABCD，所以1AABO⊥．又BOAC⊥，所以BO⊥平面11ACCA．作OHCE⊥，垂足为H，联结BH，由三垂线定理可知BHCE⊥，则O

HB为二面角1BECC−−平面角的补角．设1AB=，则12,1,2,3AAAEACCE====，由OHAEOCCE=，得66OH=．在RtBOH中，2263BHOHOB=+=，所以3sin2OBOHBBH==，即二面角1BECC−−的正弦值为32．[方法二]【利用平面的

法向量】设底面边长为1，高为2x，所以222211,1BExBEx=+=+．因为BE⊥平面11EBC，所以190BEB=，即22211BEBEBB+=，所以22224xx+=，解得1x=．因为BC⊥平面11AA

BB，所以1BCBE⊥，又1BEBE⊥，所以1BE⊥平面BCE，故1BE为平面BCE的一个法向量．因为平面1CCE与平面11AACC为同一平面，故11BD为平面1CCE的一个法向量，在11BDE中，因

为11112BDDEBE===，故1BE与11BD成60角，所以二面角1BECC−−，的正弦值为3sin602=．[方法三]【利用体积公式结合二面角的定义】设底面边长为1，高为2x，所以222211,1B

ExBEx=+=+．因为BE⊥平面11EBC，所以190BEB=，即22211BEBEBB+=，所以22224xx+=，解得1x=．因为BCBE⊥，所以BCE是直角三角形，1,3,2BCECEB===．因为1B

B∥平面1ECC，所以1,BB到平面1ECC的距离相等设为1h．同理，A，E到平面11BBC的距离相等，都为1，所以1111EBBCBECCVV−−=，即11111133BBCBCCSABSh=VV，解得122h=．设点B到直线CE的距离为2h，在BCE中，

由面积相等解得263h=．设为二面角1BECC−−的平面角，123sin2hh==，所以二面角1BECC−−的正弦值为32．[方法四]【等价转化后利用射影面积计算】由（1）的结论知1BEEB⊥，又1AEAE=

，易证11ABEABE≌，所以1145AEBAEB==，所以AEAB=，即二面角1BECC−−的正弦值与二面角BECA−−的正弦值相等．设111,,BBCCDD的中点分别为F，G，H，显然ABCDEFGH−为正方体，所求问题转化为如图3所示，在正方体ABCDEFGH−

中求二面角BECA−−的正弦值．设,ACBD相交于点O，易证BO⊥平面ACGE，所以EOC△是EBC在平面ACGE上的射影．令正方体ABCDEFGH−的棱长2ABBCAE===，则22BE=，2OC=，122BDCSOCAE==V

，1222EBCSBCBE==V．设二面角BECA−−为，由cosBDCEBCSS=VV，则21cos222BDCEBCSS===VV，所以3sin2=．即二面角1BECC−−的正弦值为32．[方法五]【结合（1）的结论找到二面角的平面角进行计算】如图4，分别

取111,,BBCCDD中点F，G，H，联结,,,EFFGGHGE．过G作GPEC⊥，垂足为P，联结BP．易得E，F，G，H共面且平行于面ABCD．由（1）可得BE⊥面11EBC．因为1BE面11EBC，所以1BEBE⊥．又

因为E为1AA中点，所以11ABEABE≌，且均为等腰三角形．设1AB=，则1AE=，四棱柱ABCDEFGH−为正方体．在GEC及BEC中有1,2,3CGCBEGEBEC=====．所以EGCV与BEC均为直角三角形且全等．又因为GPEC⊥，所以

,BPECBPG⊥为二面角BECG−−（即1BECC−−）的一个平面角．在BPG中，2,23GPBPBG===．所以222222133cos2222233BPGPGBBPGBPGP+−+−===−，所以3sin2BPG

=．故二面角1BECC−−的正弦值为32．[方法六]【最优解：空间向量法】以点B坐标原点，以1,,BCBABB分别为,,xyz轴，建立如下图所示的空间直角坐标系，1(0,0,0),(,0,0),(,0,),(0,,

)2bBCaCabEa，因为1BEEC⊥，所以2210(0,,)(,,)002224bbbBEECaaaaba=−=−+==，所以(0,,)Eaa，1(,,),(0,0,2),(0,,)ECaaaCCaBEaa=−−==，设111(,,)mxyz=是平面BEC的法向量，所以11111

0,0,(0,1,1)0.0,ayazmBEmaxayazmEC+===−−−==，设222(,,)nxyz=是平面1ECC的法向量，所以2122220,0,(1,1,0)0.0,aznCCnaxayaznCE===−−==，二面角1BECC−

−的余弦值的绝对值为11222mnmn==，所以二面角1BECC−−的正弦值为2131()22−=.【整体点评】(2)方法一：三垂线定理是立体几何中寻找垂直关系的核心定理；方法二：利用平面的法向量进行计算体

现了等价转化的数学思想，是垂直关系的进一步应用；方法三：体积公式可以计算点面距离，结合点面距离可进一步计算二面角的三角函数值；方法四：射影面积法体现等价转化的数学思想，是将角度问题转化为面积问题的一种方法；方法五：利用第一问的结

论找到二面角，然后计算其三角函数值是一种常规的思想；方法六：空间向量是处理立体几何的常规方法，在二面角不好寻找的时候利用空间向量是一种更好的方法.23．（2019·全国·高考真题）如图，直四棱柱ABCD–A1B1C1D1的底面是菱形，AA1=4，AB=2，∠BAD=60°，E，M，N分别

是BC，BB1，A1D的中点．（1）证明：MN∥平面C1DE；（2）求二面角A-MA1-N的正弦值．【答案】（1）见解析；（2）105.【分析】（1）利用三角形中位线和11//ADBC可证得//MEND，证得四边形MNDE为平行四边形，进而证得//MNDE，根据线面平

行判定定理可证得结论；（2）以菱形ABCD对角线交点为原点可建立空间直角坐标系，通过取AB中点F，可证得DF⊥平面1AMA，得到平面1AMA的法向量DF；再通过向量法求得平面1MAN的法向量n，利用向量夹角公式求得两个法向量夹角的余弦值，进而可求得所求二面角的正弦值.【详解】（1）连接ME，1B

CM，E分别为1BB，BC中点ME为1BBC的中位线1//MEBC且112MEBC=又N为1AD中点，且11//ADBC1//NDBC且112NDBC=//MEND四边形MNDE为平行四边形//MNDE，又MN平面1CDE，DE平面1CDE

//MN平面1CDE（2）设ACBDO=，11111ACBDO=由直四棱柱性质可知：1OO⊥平面ABCD四边形ABCD为菱形ACBD⊥则以O为原点，可建立如下图所示的空间直角坐标系：则：()3,0,0A，()0,1,

2M，()13,0,4A，D（0，-1,0）31,,222N−取AB中点F，连接DF，则31,,022F四边形ABCD为菱形且60BAD=BAD为等边三角形DFAB⊥又1AA⊥平面ABCD，DF平面ABCD1DFAA⊥D

F⊥∴平面11ABBA，即DF⊥平面1AMADF为平面1AMA的一个法向量，且33,,022DF=设平面1MAN的法向量(),,nxyz=r，又()13,1,2MA=−，33,,022MN=−

132033022nMAxyznMNxy=−+==−=，令3x=，则1y=，1z=−()3,1,1n=−315cos,515DFnDFnDFn===10sin,5

DFn=二面角1AMAN−−的正弦值为：105【点睛】本题考查线面平行关系的证明、空间向量法求解二面角的问题.求解二面角的关键是能够利用垂直关系建立空间直角坐标系，从而通过求解法向量夹角的余弦值来得到

二面角的正弦值，属于常规题型.24．（2018·北京·高考真题）如图，在三棱柱ABC−111ABC中，1CC⊥平面ABC，D，E，F，G分别为1AA，AC，11AC，1BB的中点，AB=BC=5，AC=1AA=2．（1）求证：AC⊥平面BEF；（2）求二面

角B−CD−C1的余弦值；（3）证明：直线FG与平面BCD相交．【答案】（1）证明见解析；（2）2121−；（3）证明见解析．【分析】（1）由等腰三角形性质得ACBE⊥，由线面垂直性质得1ACCC⊥,由

三棱柱性质可得1//EFCC，因此EFAC⊥，最后根据线面垂直判定定理得结论；（2）根据条件建立空间直角坐标系，设各点坐标，利用方程组解得平面BCD一个法向量，根据向量数量积求得两法向量夹角，再根据二面角与法向量夹角相等或互补关系求结果；（3）根据平面B

CD一个法向量与直线FG方向向量数量积不为零，可得结论.【详解】（1）在三棱柱ABC-A1B1C1中，∵CC1⊥平面ABC，∴四边形A1ACC1为矩形．又E，F分别为AC，A1C1的中点，∴AC⊥EF．∵AB=BC，E为AC的中点，．∴AC⊥BE，而BEEFB=，∴AC⊥

平面BEF．（2）［方法一］：【通性通法】向量法由（1）知AC⊥EF，AC⊥BE，EF∥CC1．又CC1⊥平面ABC，∴EF⊥平面ABC．∵BE平面ABC，∴EF⊥BE．如图建立空间直角坐称系E-xyz．由题意得B（0，2，0），C（-1，0，0），D（1

，0，1），F（0，0，2），G（0，2，1）．∴()()=201=120CDCB，，，，，，设平面BCD的法向量为()nabc=，，，∴00nCDnCB==，∴2020acab+=+=，令a=2，则b=-1，c=-4，∴平面BCD的一个法向量()21

4n=−−，，，又∵平面CDC1的一个法向量为()=020EB，，，∴21cos=21EBEBEnBnn=−．由图可得二面角B-CD-C1为钝角，所以二面角B-CD-C1的余弦值为2121−．［方法二］：【最优解】转化＋面积射影法考虑到二面角

BCDA−−与二面角1BCDC--互补，设二面角1BCDC--为，易知5DC=，6DB=，所以121,22DCEDCBSS==△△．故1212cos21212DCEDCBSS=−=−=−△△．［方法三］：转化＋三垂线法二面角BCDA−−与二面角1BCDC--互补，并设二面角

BCDA−−为，易知BE⊥平面ACD．如图3，作EHCD⊥，垂足为H，联结BH．则BHE是二面角BCDA−−的平面角，所以BHE=，不难求出21cos21=，所以二面角1BCDC--的余弦值为2121−．（3）［方法一］：【最优解】【通性通法】向量

法平面BCD的一个法向量为()214n=−−，，，∵G（0，2，1），F（0，0，2），∴()=021GF−，，，∴2nGF=−，∴n与GF不垂直，∴GF与平面BCD不平行且不在平面BCD内，∴GF与平面BCD相交．［方法二］：几何转

化如图4，取11AB的中点G，分别在11,BBCC取点N，M，使11114,4BNBBCMCC==．联结,,,FGGNNMFM．则平面DCB∥平面FGNM，又FM平面FGNM，FG平面FGNM，故直线FG

与平面BCD相交．［方法三］：根据相交的平面定义如图5，设CD与EF交于P，联结PB．因为1EFBB，且1EFBB=，所以1,,,BEFB四点共面．因为131,42PFEFBGBB==，所以PFBG．又PFBG∥，所以四边形P

FGB是梯形，即直线FG与直线BP一定相交．因为BP平面BCD，所以直线FG与平面BCD相交．【整体点评】（2）方法一：直接利用向量法求出，属于通性通法；方法二：根据二面角BCDA−−与二面角1BCDC--互补，通过转化求二面角BCDA−−，利用面积射影法求出，是该问的

最优解；方法三：根据二面角BCDA−−与二面角1BCDC--互补，通过转化求二面角BCDA−−，利用三垂线法求出；（3）方法一：利用向量证明平面的法向量与直线的方向向量不垂直即可，既是该问的通性通法，也是最优解；方法二：通过证明与平面BCD平行的平面与直线FG相交证出；方法三：

构建过直线FG且与平面BCD相交的平面，通过证明直线FG与交线相交证出．25．（2018·全国·高考真题）如图，边长为2的正方形ABCD所在的平面与半圆弧CD所在平面垂直，M是CD上异于C，D的点．（1）证明：平面AMD⊥平面BMC；（2）当三棱

锥MABC−体积最大时，求面MAB与面MCD所成二面角的正弦值．【答案】（1）证明见解析；（2）255．【分析】（1）方法一：先证BC⊥平面CMD,得BCDM⊥,再证CMDM⊥，由线面垂直的判定定理可得DM⊥平面BMC，即可根

据面面垂直的判定定理证出；（2）方法一：先建立空间直角坐标系，然后判断出M的位置，求出平面MAB和平面MCD的法向量，进而求得平面MAB与平面MCD所成二面角的正弦值．【详解】（1）［方法一］：【最优解

】判定定理由题设知,平面CMD⊥平面ABCD,交线为CD.因为BC⊥CD,BC平面ABCD,所以BC⊥平面CMD,故BC⊥DM.因为M为CD上异于C，D的点,且DC为直径，所以DM⊥CM.又BCCM=C,所以DM⊥平面BMC.而DM平面AMD,故平面A

MD⊥平面BMC.［方法二］：判定定理由题设知,平面CMD⊥平面ABCD,交线为CD.因为ADCD⊥，AD平面ABCD,所以AD⊥平面MCD，而CM平面MCD，所以AD⊥CM，因为M为CD上异于C，D的点,且

DC为直径，所以DM⊥CM.又ADDMD=，所以，CM⊥平面AMD，而CM平面BMC，所以平面AMD⊥平面BMC．［方法三］：向量法建立直角坐标系，如图2，设(0,,)Mab，()()()()0,0,0,2,0,0,2,2,0,0,2,0,DABC所以()(

)2,0,0,0,,DADMab==，设平面AMD的一个法向量为()111,,mxyz=，所以=0=0nDAnDM，即1112=0+=0xaybz，取平面AMD的一个法向量(0,,)mba=−，同理可得，平面BMC的一个法向量(0,,2)nba=−，因为点M在以()0,1,0

为圆心，半径为1的圆上，所以，()2211ab−+=，即2220aba+−=，而2220banam+=−=，所以平面AMD⊥平面BMC．（2）［方法一］：【通性通法】向量法以D为坐标原点,DA的方向为x轴正方向,建立如图所示的空间直角坐标系D−xyz.当

三棱锥M−ABC体积最大时，M为CD的中点.由题设得()()()()()0,0,0,2,0,0,2,2,0,0,2,0,0,1,1DABCM，()()()2,1,1,0,2,0,2,0,0AMABDA=−==设(),,nxyz=是平面MAB的法向

量,则=0=0nAMnAB即2++=02=0xyzy−，可取()1,0,2n=.DA是平面MCD的一个法向量,因此5cos,5DADDAnAnn==，25sin,5nDA=

，所以面MAB与面MCD所成二面角的正弦值是255.［方法二］：几何法（作平行线找公共棱）如图3，当点M与圆心O连线MODC⊥时，三棱锥MABC−体积最大．过点M作,,EFDCEDDCFCDC⊥⊥∥，易证BFC为所求二面角的平面角．在RtBCF

△中，25sin5BCBFCBF==，即面MAB与面MCD所成二面角的正弦值是255．［方法三］：【最优解】面积射影法设平面MAB与平面MCD所成二面角的平面角为．由题可得MAB△在MCD△平面上的射影图形正好是MCD△．取AB和CD的中点分别

为N和O，则可得1OM=，5MN=，所以由射影面积公式有1cos5MCDMABSS==△△，所以25sin5=，即面MAB与面MCD所成二面角的正弦值是255．［方法四］：定义法如图4，可知平面MAB与平面MCD的交线l过点M，可以证明,lABlCD∥

∥．分别取,CDAB的中点O，E，联结,,OEMOME，可证得直线CD⊥平面OME，于是l⊥平面OME，所以,lMOlME⊥⊥，故OME是面MAB与面MCD所成二面角的平面角．在OME△中，,1,2MOOEMOOE⊥==，则5ME=，所以25sin5OME=，即面MAB与面MCD所成

二面角的正弦值为255．【整体点评】（1）方法一：利用面面垂直的判定定理寻找合适的线面垂直即可证出，是本题的最优解；方法二：同方法一，只不过找的线面垂直不一样；方法三：利用向量法，计算两个平面的法向量垂直即可，思路简单，运算较繁．（2）方法一

：直接利用向量法解决无棱二面角问题，是该类型题的通性通法；方法二：作平行线找公共棱，从而利用二面角定义找到二面角的平面角，是传统解决无棱二面角问题的方式；方法三：面积射影法也是传统解决无棱二面角问题的方式，是本题的最优解；方法四：同方法二

，通过找到二面角的公共棱，再利用定义找到平面角，即可解出．26．（2017·山东·高考真题）如图，几何体是圆柱的一部分，它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的，G是DF的中点.(1)设P是CE上的一点，且AP⊥BE，求∠CBP的大小；(2)当

AB＝3，AD＝2时，求二面角E－AG－C的大小.【答案】（1）30；（2）60【分析】试题分析:(1)第(1)问,直接证明BE⊥平面ABP得到BE⊥BP,从而求出∠CBP的大小.(2)第（2）问，可以利用几何法求，也可以利用向量法求解.【详解】解：(1)因为

AP⊥BE，AB⊥BE，AB，AP⊂平面ABP，AB∩AP＝A，所以BE⊥平面ABP.又BP⊂平面ABP，所以BE⊥BP.又∠EBC＝120°，所以∠CBP＝30°.(2)方法一：如图，取EC的中点H，连接EH，GH，CH.因为∠EBC＝120°，所以四边

形BEHC为菱形，所以AE＝GE＝AC＝GC＝223213+=.取AG的中点M，连接EM，CM，EC，则EM⊥AG，CM⊥AG，所以∠EMC为所求二面角的平面角．又AM＝1，所以EM＝CM＝13123−=.在△BEC中，由于∠EBC＝12

0°，由余弦定理得EC2＝22＋22－2×2×2×cos120°＝12，所以EC＝23，所以△EMC为等边三角形，故所求的角为60°.方法二：以B为坐标原点，分别以BE，BP，BA所在的直线为x，y，z轴，建立如图所示的空间直角坐标系B－xyz.由题意得A(0,0,3)，E(2,0,0)

，G(1，3，3)，C(－1，3，0)，故AE＝(2,0，－3)，AG＝(1，3，0)，CG＝(2,0,3)．设m＝(x1，y1，z1)是平面AEG的一个法向量，由00mAEmAG==可得11112

3030xzxy−=+=取z1＝2，可得平面AEG的一个法向量m＝(3，－3，2)．设n＝(x2，y2，z2)是平面ACG的一个法向量．由00nAGnCG==可得222230230xyxz+=+=取z2＝－2，可得平面ACG的一个法向量n＝(3，－3

，－2)．所以cos〈,mn〉＝||||mnmn＝12.故所求的角为60°.点睛：本题的难点主要是计算，由于空间向量的运算，所以大家在计算时，务必仔细认真.27．（2017·全国·高考真题）（2017新课标全国Ⅲ理科）如图，四面

体ABCD中，△ABC是正三角形，△ACD是直角三角形，∠ABD=∠CBD，AB=BD．（1）证明：平面ACD⊥平面ABC；（2）过AC的平面交BD于点E，若平面AEC把四面体ABCD分成体积相等的两部分，求二面角D–AE–C的余弦值.【答案】（1）见解析；（2）77.【详解】试

题分析：（1）利用题意证得二面角的平面角为90°，则可得到面面垂直；（2）利用题意求得两个半平面的法向量，然后利用二面角的夹角公式可求得二面角D–AE–C的余弦值为77.试题解析：（1）由题设可得，ABDCBD≌△△，从而ADDC=.

又ACD是直角三角形，所以=90ADC.取AC的中点O，连接DO,BO,则DO⊥AC,DO=AO.又由于ABC是正三角形，故BOAC⊥.所以DOB为二面角DACB−−的平面角.在RtAOB中，222BOAOAB+=.又ABBD=，所以222222BODOB

OAOABBD+=+==，故90DOB=.所以平面ACD⊥平面ABC.（2）由题设及（1）知，,,OAOBOD两两垂直，以O为坐标原点，OA的方向为x轴正方向，OA为单位长，建立如图所示的空间直角坐标系Oxyz−.则()()()()1,0,0,0,3,0,1,0,0,

0,0,1ABCD−.由题设知，四面体ABCE的体积为四面体ABCD的体积的12，从而E到平面ABC的距离为D到平面ABC的距离的12，即E为DB的中点，得310,,22E.故()()311

,0,1,2,0,0,1,,22ADACAE=−=−=−.设(),,nxyz=是平面DAE的法向量，则00nADnAE==，，即0,310.22xzxyz−+=−++=可取31,,13=n.设m是平面

AEC的法向量，则00mACmAE==，，同理可取()0,1,3=−m.则7cos,7==nmnmnm.所以二面角D-AE-C的余弦值为77.【名师点睛】（1）求解本题要注意两点：一是两平面的法向量的夹角不一定是所求的二面角，二是利用方程思想进行向量运算时，要认真细心，准确

计算.（2）设m，n分别为平面α，β的法向量，则二面角θ与,mn互补或相等，故有coscos,mnmnmn==.求解时一定要注意结合实际图形判断所求角是锐角还是钝角.28．（2017·全国·高考真题）如图，在四棱锥P−ABCD中，AB//CD，且90BAPCDP==.（1）证明：平面PAB

⊥平面PAD；（2）若PA=PD=AB=DC，90APD=，求二面角A−PB−C的余弦值.【答案】（1）见解析；（2）33−.【详解】（1）由已知90BAPCDP==，得AB⊥AP，CD⊥PD．由于AB//CD，故A

B⊥PD，从而AB⊥平面PAD．又AB平面PAB，所以平面PAB⊥平面PAD．（2）在平面PAD内作PFAD⊥，垂足为F，由（1）可知，AB⊥平面PAD，故ABPF⊥，可得PF⊥平面ABCD.以F为坐标原点，FA的方向为x轴正方向，AB为单位

长，建立如图所示的空间直角坐标系Fxyz−.由（1）及已知可得2,0,02A，20,0,2P，2,1,02B，2,1,02C−.所以22,1,22PC=−−，()2,0,0CB=，22,0,22PA=−

，()0,1,0AB=.设(),,nxyz=r是平面PCB的法向量，则0,0,nPCnCB==即220,2220,xyzx−+−==可取()0,1,2n=−−.设(),,mxyz=是平面PAB的法向量，则0,0,mPAmA

B==即220,220.xzy−==可取()1,0,1m=.则3cos,3nmnmnm==−，所以二面角APBC−−的余弦值为33−.【名师点睛】高考对空间向量与立体几何的考查主要体现在以下几个方面：①求异面直线所成的角，关键是转化为两

直线的方向向量的夹角；②求直线与平面所成的角，关键是转化为直线的方向向量和平面的法向量的夹角；③求二面角，关键是转化为两平面的法向量的夹角.建立空间直角坐标系和表示出所需点的坐标是解题的关键.29．（2017·江苏·高考真题）如图，在平行六面体A

BCD－A1B1C1D1中，AA1⊥平面ABCD，且AB＝AD＝2，AA1＝3，∠BAD＝120°.(1)求异面直线A1B与AC1所成角的余弦值；(2)求二面角B－A1D－A的正弦值．【答案】(1)1

7．(2)74．【详解】试题解析：解：在平面ABCD内，过点A作AE⊥AD，交BC于点E.因为AA1⊥平面ABCD，所以AA1⊥AE，AA1⊥AD.如图，以1,,AEADAA为正交基底，建立空间直角坐标系A-xyz.因

为AB=AD=2，AA1=3，120BAD=.则()()()()()()110,0,0,3,1,0,0,2,0,3,0,0,0,0,3,3,1,3ABDEAC−.(1)()()113,1,3,3,1,3ABAC=−−=，则()()111

1113,1,33,1,31cos,77ABACABACABAC−−===−.因此异面直线A1B与AC1所成角的余弦值为17.(2)平面A1DA的一个法向量为()3,0,0AE=.设(),,mxyz=为平面BA1D的一个法向量，又()()13,1,3

,3,3,0ABBD=−−=−，则10,0,mABmBD==即330,330.xyzxy−−=−+=不妨取x=3，则3,2yz==，所以()3,3,2m=为平面BA1D的一个法向量，从而()()3,0,03,3,23

,434AEmcosAEmAEm===,设二面角B-A1D-A的大小为，则3cos4=.因为0,，所以271cos4sin=−=.因此二面角B-A1D-A的正弦值为74.30．（2016·天津·高考真题）如

图，正方形ABCD的中心为O，四边形OBEF为矩形，平面OBEF⊥平面ABCD，点G为AB的中点，AB=BE=2.（Ⅰ）求证：EG∥平面ADF；（Ⅱ）求二面角O−EF−C的正弦值；（Ⅲ）设H为线段AF上的点，且AH=23HF，求直线B

H和平面CEF所成角的正弦值.【答案】（Ⅰ）详见解析；（Ⅱ）33；（Ⅲ）721.【详解】试题分析：（Ⅰ）利用空间向量证明线面平行，关键是求出平面的法向量，利用法向量与直线方向向量垂直进行论证；（Ⅱ）利用空间向量求二面角，关键是求出平面的法向量，再利用向量数量积求出法向量夹角，最后根据向量夹角与二面

角相等或互补关系求正弦值；（Ⅲ）利用空间向量求线面角，关键是求出平面的法向量，再利用向量数量积求出向量夹角，最后根据向量夹角与线面角互余关系求正弦值.试题解析：依题意，OFABCD⊥平面，如图，以O为点，分别以,,ADBAOF的方向为x轴、y轴、z轴的正

方向建立空间直角坐标系，依题意可得(0,0,0)O，()1,1,0,(1,1,0),(1,1,0),(11,0),(1,1,2),(0,0,2),(1,0,0)ABCDEFG−−−−−−−，.（Ⅰ）证明：依题意，()(2,0,0),1,1,2ADAF==−.设()1,,nxy

z=为平面ADF的法向量，则110{0nADnAF==，即20{20xxyz=−+=.不妨设1z=，可得()102,1n=,，又()0,1,2EG=−，可得10EGn=，又因为直线EGADF平面，所以//EGADF平面.（Ⅱ）

解：易证，()1,1,0OA=−为平面OEF的一个法向量.依题意，()()1,1,0,1,1,2EFCF==−.设()2,,nxyz=为平面CEF的法向量，则220{0nEFnCF==，即0{20xyxyz+=−++=.不妨设1x

=，可得()21,1,1n=−.因此有2226cos,3OAnOAnOAn==−，于是23sin,3OAn=，所以，二面角OEFC−−的正弦值为33.（Ⅲ）解：由23AHHF=，得25AHAF=.因为，所以2224,,5555AHAF==−，

进而有334,,555H−，从而284,,555BH=，因此2227cos,21BHnBHnBHn==−.所以，直线BH和平面CEF所成角的正弦值为721.【考点】利用空间向量解决立体几何问题31．（2016·山东·

高考真题）在如图所示的圆台中，AC是下底面圆O的直径，EF是上底面圆O'的直径，FB是圆台的一条母线.（Ⅰ）已知G,H分别为EC，FB的中点，求证：GH∥平面ABC；（Ⅱ）已知EF=FB=12AC=23，AB=BC．求二面角FBCA−−的余弦值.【答案】（Ⅰ）见解析

；（Ⅱ）77【详解】(Ⅰ)连结FC，取FC的中点M，连结GM，HM，//GMEF、EF在上底面内，GM不在上底面内，//GM上底面，//GM平面ABC，又MH//BC，BC平面ABC，MH平面ABC，H//M平面ABC，所以平面GHM//平面ABC，由GH平面GHM

，GH//平面ABC．(Ⅱ)连结OB，ABBC=，OAOB⊥，以O为原点，分别以OA，OB，'OO为x，y，z轴建立空间直角坐标系，1232EFFBAC===，ABBC=，()223OOBFBOFO=−−=，于是有()23,

0,0A，()23,0,0C−，()0,23,0B，()0,3,3F，可得平面FBC中的向量()0,3,3BF=−，()23,23,0CB=，设平面FBC中的法向量(),,nxyz=r，则33023230nBFyznCBxy=−+==+=于是得平面FBC的一个法向量

，又平面ABC的一个法向量()20,0,1n=设二面角FBCA−−为，则121217cos77nnnn===，二面角FBCA−−的余弦值为77.考点：直线与平面平行的判定；二面角的平面及求法.【方法点晴】本题考查线面平行的证明，考查二面角的余弦值

的求法，是中档题，解题时要认真审题，注意向量法的合理运用；直线与平面平行的判定定理的实质是：对于平面外的一条直线，只需在平面内找到一条直线和这条直线平行，就可判定这条直线必和这个平面平行．即由线线平行得到线面平行，向量法：两平面所成的角的大小

与分别垂直于这平面的两向量所成的角（或补角）相等.32．（2016·浙江·高考真题）如图,在三棱台ABCDEF−中,平面BCFE⊥平面ABC,90,2ACBBC==，3,1ACBEEFFC====.（Ⅰ）求证：BF⊥平面ACFD；

（Ⅱ）求二面角BADF−−的平面角的余弦值.【答案】（Ⅰ）见解析；（Ⅱ）34．【分析】（Ⅰ）延长AD，BE，CF相交于一点K，先证BFAC⊥，再证BFCK⊥，进而可证F⊥平面ACFD；（Ⅱ）方法一：先找二面角BADF−−的平面角，再在RtBQF△中计算，即可得二面

角BADF−−的平面角的余弦值；方法二：先建立空间直角坐标系，再计算平面ACK和平面ABK的法向量，进而可得二面角BADF−−的平面角的余弦值．【详解】（Ⅰ）延长AD，BE，CF相交于一点K，如图所示．因为平面BCFE⊥平面ABC，平面BCFE平面ABCBC=，且ACBC⊥，所以AC⊥平面

BCK，BF平面BCK，因此BFAC⊥．又因为//EFBC，1BEEFFC===，2BC=，所以BCK为等边三角形，且F为CK的中点，则,BFCKCKACC⊥=．所以BF⊥平面ACFD．（Ⅱ）方法一：过点F作FQAK⊥于Q，连结BQ．

因为BF⊥平面ACK，所以BFAK⊥，BFFQF=，则⊥AK平面BQF，所以BQAK⊥．所以BQF是二面角BADF−−的平面角．在RtACK中，3AC=，2CK=，得31313FQ=．在RtBQF△中

，31313FQ=，3BF=，得3cos4BQF=．所以二面角BADF−−的平面角的余弦值为34．方法二：如图，延长,,ADBECF相交于一点K，则BCK为等边三角形．取BC的中点O，则KOBC⊥，又平面BCFE⊥平面ABC，所以，K

O⊥平面ABC．以点O为原点，分别以射线OB，OK的方向为x，z的正方向，建立空间直角坐标系Oxyz．由题意得()1,0,0B，()1,0,0C−，(0,0,3)K，()1,3,0A−−，13(,0,)22E

，13(,0,)22F−．因此，()0,3,0AC=，()1,3,3AK=，()2,3,0AB=．设平面ACK的法向量为111(,,)mxyz=，平面ABK的法向量为222(,,)nxyz=．由00ACmAKm==，

得111130330yxyz=++=，取()3,0,1m=−；由00ABnAKn==，得22222230330xyxyz+=++=取()3,2,3n=−．于是，3333cos,431943mnmnmn−===+++．所以，二面角BADF−−的平面角的余弦值

为34．【点睛】解题时一定要注意二面角的平面角是锐角还是钝角，否则很容易出现错误．证明线面垂直的关键是证明线线垂直，证明线线垂直常用的方法是直角三角形、等腰三角形的“三线合一”和菱形、正方形的对角线．33．（2016·

全国·高考真题）如图，菱形ABCD的对角线AC与BD交于点,5,6OABAC==，点,EF分别在,ADCD上，5,4AECFEF==交BD于点H，将DEF沿EF折到DEF位置，10OD=.（1）证明：DH⊥平面ABCD；（2）求二面角BDAC−−的正弦值.【答案】（

1）证明见解析；（2）29525.【详解】试题分析：(1)证明线面垂直，一般利用线面垂直判定定理，即利用线线垂直进行论证，而线线垂直的寻找与论证往往需要利用平面几何条件，如本题需利用勾股定理经计算得出线垂直

（2）一般可利用空间向量的数量积求二面角的大小，首先根据题意建立恰当的直角坐标系，设立各点坐标，利用方程组解出各面的法向量，再根据向量数量积求出两个法向量的夹角的余弦值，最后根据二面角与法向量夹角关系确定二面角的余弦值.试题解析：(1)由已知得ACBD⊥，ADCD=,又由

AECF=得AECFADCD=，故AC∥EF，因此EFHD⊥，从而EF⊥DH.由56ABAC==，得224DOBOABAO==−=.由AC∥EF得14OHAEDOAD==.所以1OH=,3DHDH==.于是222223110DHOHDO+=+==,故DHOH⊥.又DHE

F⊥,而OHEFH=,所以DH⊥平面ABCD.如图，以H为坐标原点，HF的方向为x轴的正方向，建立空间直角坐标系Hxyz−，则()0,0,0H，()3,1,0A−−，()0,6,0B−，()3,1,0C−，()0,0,3D

，()3,4,0AB=−，()6,0,0AC=，()3,1,3AD=.设()111,,mxyz=r是平面ABD的法向量，则0{0mABmAD==，即11111340{330xyxyz−=++

=，可取()4,3,5m=−.设()222,,nxyz=r是平面ACD的法向量，则0{0nACnAD==，即222260{330xxyz=++=，可取()0,3,1n=−于是1475cos,255010mnmnmn

−===−，设二面角的大小为，295sin25=.因此二面角BDAC−−的正弦值是29525.点睛：利用法向量求解空间线面角的关键在于“四破”：第一，破“建系关”，构建恰当的空间直角坐标系；第二，破“求坐标关”，准确求解

相关点的坐标；第三，破“求法向量关”，求出平面的法向量；第四，破“应用公式关”.34．（2016·全国·高考真题）如图，在以A，B，C，D，E，F为顶点的五面体中，四边形ABEF为正方形，2AFFD=

，90AFD=，且二面角DAFE−−与二面角CBEF−−都是60.（1）证明：平面ABEF⊥平面EFDC；（2）求二面角EBCA−−的余弦值.【答案】（1）见解析；（2）21919−.【分析】（Ⅰ）证明AF⊥平面EFDC，结合

AF平面ABEF，可得平面ABEF⊥平面EFDC．（Ⅱ）建立如图所示的空间坐标系，求出平面EBC的法向量和平面BCA的法向量的夹角的余弦值后可得所求的二面角的余弦值.【详解】（Ⅰ）因为四边形ABEF

为正方形，所以AFFE⊥，又AFDF⊥，DFFEF=，所以AF⊥平面EFDC．又AF平面ABEF，故平面ABEF⊥平面EFDC．（Ⅱ）过D作DGEF⊥，垂足为G，因为平面ABEF⊥平面EFDC，平面ABEF平面EFDCEF=，DG平面EFDC，故D

G⊥平面ABEF．以G为坐标原点，GF的方向为x轴正方向，GD的方向为z轴正向，建立如图所示的空间直角坐标系Gxyz−．由（Ⅰ）知DFE为二面角DAFE−−的平面角，故60DFE=，设()20DFaa=，则3DGa=，FGa=，所以(),4,0Aaa，()3,4,0Baa−，()3,

0,0Ea−，()0,0,3Da．由已知，//ABEF，而AB平面EFDC，EF平面EFDC，所以//AB平面EFDC，又平面ABCD平面EFDCDC=，AB平面ABCD，故//ABCD，所以//CDEF．由//BEAF，可得BE⊥平面EFDC，同理CEF为二面角CBEF−−的平

面角，所以60CEF=，从而可得()2,0,3Caa−．所以(),0,3ECaa=，()0,4,0EBa=，()3,4,3ACaaa=−−，()4,0,0ABa=−．设(),,nxyz=是平面BCE的法向量，则00nEC

nEB==，即3040axazay+==，取3x=，则0,3yz==−，可取()3,0,3n=−．设m是平面ABCD的法向量，则00mACmAB==，同理可取()0,3,4m=，则43219cos,192319nmnmnm

==−=−．因为二面角EBCA−−的平面角为钝角，故二面角EBCA−−的余弦值为21919−．【点睛】立体几何解答题第一问通常考查线面位置关系的证明,空间中线面位置关系的证明主要包括线线、线面、面面三者的平行与垂直关系,其中推理论证

的关键是结合空间想象能力进行推理,注意防止步骤不完整或考虑不全致推理片面,该类题目难度不大,以中档题为主.第二问一般考查角度问题,多用空间向量法解决.35．（2015·广东·高考真题）如图，三角形△PDC所在的平面与长方形ABCD所在的平面垂直，PD＝PC＝4，AB＝6，

BC＝3，点E是CD的中点，点F、G分别在线段AB、BC上，且AF＝2FB，CG＝2GB．（1）证明：PE⊥FG；（2）求二面角P﹣AD﹣C的正切值；（3）求直线PA与直线FG所成角的余弦值．【答案】（1）见解析；（2）73；（3）9525．【分析】（1）通过△PDC为等腰三角形可得PE⊥CD，

利用线面垂直判定定理及性质定理即得结论；（2）通过（1）及面面垂直定理可得PG⊥AD，则∠PDC为二面角P﹣AD﹣C的平面角，利用勾股定理即得结论；（3）连结AC，利用勾股定理及已知条件可得FG∥AC，在△PAC中，利用余弦定理即得直线PA与直线FG所成角的余弦值．【详解】（1）证明：

在△PDC中PO＝PC且E为CD中点，∴PE⊥CD，又∵平面PDC⊥平面ABCD，平面PDC∩平面ABCD＝CD，PE⊂平面PCD，∴PE⊥平面ABCD，又∵FG⊂平面ABCD，∴PE⊥FG；（2）解：由（1）知PE⊥平面ABCD，∴P

E⊥AD，又∵CD⊥AD且PE∩CD＝E，∴AD⊥平面PDC，又∵PD⊂平面PDC，∴AD⊥PD，又∵AD⊥CD，∴∠PDC为二面角P﹣AD﹣C的平面角，在Rt△PDE中，由勾股定理可得：PE2222437PDDE=−=−=，∴tan∠PDC73PGDG==

；（3）解：连结AC，则AC2263=+=35，在Rt△ADP中，AP222234ADDP=+=+=5，∵AF＝2FB，CG＝2GB，∴FG∥AC，∴直线PA与直线FG所成角即为直线PA与直线AC所成角∠PAC

，在△PAC中，由余弦定理得cos∠PAC2222PAACPCPAAC+−=2225(35)42535+−=9525=．【点睛】本题考查线线垂直的判定、二面角及线线角的三角函数值，涉及到勾股定理、余弦定理等知识，注意解题

方法的积累，属于中档题．36．（2015·重庆·高考真题）如图，三棱锥−PABC中，PC⊥平面ABC，3PC=，2ACB=．,DE分别为线段,ABBC上的点，且2,22CDDECEEB====．(1)证明：DE⊥平面PCD；(2)

求二面角APDC−−的余弦值．【答案】（1）见解析；（2）36【详解】试题分析：（1）要证线面垂直，就是要证线线垂直，题中由PC⊥平面ABC，可知PCDE⊥，再分析已知由2,2DCDECE===得CDDE⊥，这样与DE垂直的两条直线都已找到，从而可得线面垂直；（2）求二面角的大小，可心根据

定义作出二面角的平面角，求出这个平面角的大小，本题中，由于2ACB=，PC⊥平面ABC，因此,,CACBCP两两垂直，可以他们为,,xyz轴建立空间直角坐标系，写出图中各点的坐标，求出平面APD和平面CPD的法向量12,nn，向量12,nn的夹角与二面角相等或互补，由此可得结论

．试题解析：（1）证明：由PC⊥平面ABC，DE平面ＡＢＣ，故PC⊥DE由CE＝２，CD=DE＝２得ＣＤＥ为等腰直角三角形，故CD⊥DE由PCCD=C，DE垂直于平面PCD内两条相交直线，故DE⊥平面PCD（2）解：由（１）知，CDE为等腰直角三角形，DCE＝4,

，如（１９）图，过点Ｄ作DF垂直CE于Ｆ，易知DF＝FC＝EF＝１，又已知EB＝１，故FB＝２．由ACB＝2,得DF//AC，23DFFBACBC==，故AC＝32DF＝32．以Ｃ为坐标原点，分别以,CACBCP，的方程为x轴，y轴，z轴的正方向建立空间直角坐标系，则Ｃ（

0,0,0,），Ｐ（0,0,3），Ａ（32,0,0）,Ｅ（0,2,0），Ｄ（1,1,0），(1,1,0),ED=−(1,1,3)(,1,0)DPDA１，２=−−=−设平面PAD的法向量111,,)nxyz１＝（，由0nDP

=１，0nDA=１，得11111130{(2,1,10+)12xyznxy故可取−−==−=.由（1）可知DE⊥平面PCD，故平面PCD的法向量2nuur可取为ED,即2(1,1,0)n=−.从而法向量1nur，2nuur的夹角的余弦值为1212123,=6||||nncosnnnn

=，故所求二面角A-PD-C的余弦值为36.考点：考查线面垂直，二面角．考查空间想象能力和推理能力．37．（2015·浙江·高考真题）如图，在三棱柱111ABCABC--中，90BAC=，2ABA

C==，14AA=，1A在底面ABC的射影为BC的中点，D为11BC的中点.（1）证明：1AD⊥平面1ABC；（2）求二面角1A-BD-1B的平面角的余弦值.【答案】（1）详见解析；（2）18−.【详解】（1）根据条件首先证得⊥AE平面1ABC，再证明1/

/ADAE，即可得证；（2）作1AFBD⊥，且，可证明11AFB为二面角11ABDB−−的平面角，再由余弦定理即可求得111cos8AFB=−，从而求解.试题解析：（1）设E为BC的中点，由题意得1AE⊥平面ABC，∴1AEAE⊥，∵A

BAC=，∴AEBC⊥，故⊥AE平面1ABC，由D，E分别11BC，BC的中点，得1//DEBB且1DEBB=，从而1//DEAA，∴四边形1AAED为平行四边形，故1//ADAE，又∵⊥AE平面11ABC，∴1AD⊥平面11ABC；（2）作1AFBD⊥，且，连结1BF，由2

AEEB==，1190AEAAEB==，得114ABAA==，由11ADBD=，11ABBB=，得11ADBBDB，由1AFBD⊥，得1BFBD⊥，因此11AFB为二面角11ABDB−−的平面角，由12AD=，14A

B=，190DAB=，得32BD=，1143AFBF==，由余弦定理得，111cos8AFB=−.考点：1.线面垂直的判定与性质；2.二面角的求解38．（2015·四川·高考真题）一个正方体的平面展开图及该正方体的直观图的示意图如图所示，在正方体中，设BC的中点为M，GH的中点为N(1

)请将字母,,FGH标记在正方体相应的顶点处（不需说明理由）(2)证明：直线//MN平面BDH(3)求二面角AEGM−−的余弦值.【答案】(1)见解析(2)证明见解析(3)223【分析】（1）根据展开图在图中作出.（2）线面线面平行的判定即可；（3）根据二面角定义作出该角，

求出其余弦值即可.【详解】（1）点F、G、H的位置如图所示.（2）连结BD，设O为BD的中点.因为M、N分别是BC、GH的中点，所以//NHCD，且12NHCD=，//MNOH，且12NHCD=，所以//,OMNHOMNH=，所以PKM是平行四边形，从而MPAC⊥，又OH平面BDH，//M

N平面BDH，MN平面BDH，所以//MN平面BDH.（3）连结AC，过M作//ACEG于P.在正方形1,2CMPK==中，//ACEG，所以KMEG⊥.过P作PKEG⊥于K，连结KM，因为KMPKK=，且,KMPK平面PKM，所以EG⊥平面PKM，又因为KM平面PKM，从而KMEG⊥.

所以PKM是二面角AEGM−−的平面角.设2AD=，则1,2CMPK==，在RtCMP中，2sin452PMCM==.在RtKMP中，22322KMPKPM=+=.所以22cos3PKPKMKM==.即二面

角AEGM−−的余弦值为223.39．（2015·陕西·高考真题）如图1，在直角梯形CD中，D//C，D2=，C1==，D2=，是D的中点，是C与的交点．将沿折起到1的位置，如图2．（Ⅰ）证明：CD⊥平面1C；（Ⅱ）若平面1

⊥平面CD，求平面1C与平面1CD夹角的余弦值．【答案】（Ⅰ）证明见解析；（Ⅱ）63．【详解】试题分析：（Ⅰ）先证1⊥，C⊥，再可证⊥平面1C，进而可证CD⊥平面1C；（Ⅱ

）先建立空间直角坐标系，再算出平面1C和平面1CD的法向量，进而可得平面1C与平面1CD夹角的余弦值．试题解析：（Ⅰ）在图1中，因为C1==，D2=，是D的中点，D2=，所以C⊥即在图2中，1⊥，C⊥从而⊥平面1AOC又CD//

，所以CD⊥平面1AOC．（Ⅱ）由已知，平面1ABE⊥平面CD，又由（Ⅰ）知，1OA⊥，C⊥所以1AOC为二面角1--CABE的平面角，所以1OC2A=．如图，以为原点，建立空间直角坐标系，因为11B=E=BC=ED=1AA，/

/BCED所以12222(,0,0),(,0,0),(0,0,),(0,,0),2222BEAC−得22(,,0),22BC−122(0,,)22AC−，(2,0,0)CDBE==−．设平面1BCA的法向量1111(,,)nxyz=，平面1CDA的法向量2222(

,,)nxyz=，平面1BCA与平面1CDA夹角为，则1110{0nBCnAC==，得11110{0xyyz−+=−=，取1(1,1,1)n=，2210{0nCDnAC==，得2220{0xyz=−=，取2(0,1,1)n=，从而1226cos,

332cosnn===，即平面1BCA与平面1CDA夹角的余弦值为63．考点：1、线面垂直；2、二面角；3、空间直角坐标系；4、空间向量在立体几何中的应用．40．（2015·山东·高考真题）如图

，在三棱台DEFABC−中，2,,ABDEGH=分别为,ACBC的中点．（Ⅰ）求证：//BD平面FGH；（Ⅱ）若CF⊥平面ABC,,ABBCCFDE⊥=，45BAC=，求平面FGH与平面ACFD所成角（锐角）的大小．【答案】（Ⅰ）略；（Ⅱ）60【详解】试题分析：（Ⅰ）思路一：连接,DG

CD，设CDGFO=，连接OH，先证明//OHBD，从而由直线与平面平行的判定定理得//BD平面HDF；思路二：先证明平面//FGH平面ABED，再由平面与平面平行的定义得到//BD平面HDF.（Ⅱ）思路一：连接,DGC

D，设CDGFO=，连接OH，证明,,GBGCGD两两垂直,以G为坐标原点，建立如图所示的空间直角坐标系Gxyz−，利用空量向量的夹角公式求解；思路二：作HMAC⊥于点M，作MNGF⊥于点N，连接NH，证明MNH即为所求的角，然后在三角形中求解

.试题解析：（Ⅰ）证法一：连接,DGCD，设CDGFO=，连接OH，在三棱台DEFABC−中，2,ABDEG=为AC的中点可得//,DFGCDFGC=所以四边形DFCG为平行四边形则O为CD的中点又H为BC的中点所以//OHBD又OH平面

,FGHBD平面,FGH所以//BD平面FGH．证法二：在三棱台DEFABC−中，由2,=BCEFH为BC的中点可得//,,BHEFBHEF=所以四边形BHFE为平行四边形可得//BEHF在ABC中，G为AC的中点，H为BC的中点，所以//GHAB又GHHFH

=，所以平面//FGH平面ABED因为BD平面ABED所以//BD平面FGH（Ⅱ）解法一：设2AB=，则1CF=在三棱台DEFABC−中，G为AC的中点由12DFACGC==，可得四边形DGCF为平行四边形，因此//DGCF又FC⊥平面ABC所以D

G⊥平面ABC在ABC中，由,45ABBCBAC⊥=，G是AC中点，所以,ABBCGBGC=⊥因此,,GBGCGD两两垂直,以G为坐标原点，建立如图所示的空间直角坐标系Gxyz−所以()()()()0,0,0,2,0,0,0,2,0,0,

0,1GBCD可得()22,,0,0,2,122HF故()22,,0,0,2,122GHGF==设(),,nxyz=是平面FGH的一个法向量，则由0,{0,nGHnGF==可得0{20xyyz+=+=可得平面FGH的一个法向量()1,1,2n=−因为GB是平

面ACFD的一个法向量，()2,0,0GB=所以21cos,222GBnGBnGBn===所以平面与平面所成的解（锐角）的大小为60解法二：作HMAC⊥于点M，作MNGF⊥于点N，连接NH由FC⊥平面ABC，得HMFC⊥又FCACC=所以HM⊥平面ACFD因此GFNH⊥

所以MNH即为所求的角在BGC中,12//,,22MHBGMHBG==由GNM∽GCF可得,MNGMFCGF=从而66MN=由MH⊥平面,ACFDMN平面ACFD得,MHMN⊥因此tan3HMMNHMN==所以60MNH=所以平面FGH与平面ACFD

所成角（锐角）的大小为60.考点：1、空间直线与平面的位置关系；2、二面角的求法；3、空间向量在解决立体几何问题中的应用.41．（2015·安徽·高考真题）如图所示，在多面体111ABDDCBA，四边形11AABB，1

1,ADDAABCD均为正方形，E为11BD的中点，过1,,ADE的平面交1CD于F.（Ⅰ）证明：1//EFBC；（Ⅱ）求二面角11EADB−−余弦值.【答案】（Ⅰ）1//EFBC；（Ⅱ）63.【详解】试题分析：（Ⅰ）证明：依据正方形的性质可知11////ABABDC，且

11ABABDC==，，从而11ABCD为平行四边形，则11//BCAD，根据线面平行的判定定理知1//BC面1ADE，再由线面平行的性质定理知1//EFBC.（Ⅱ）因为四边形11AABB，11ADDA，A

BCD均为正方形，所以11,,AAABAAADADAB⊥⊥⊥，且1AAABAD==，可以建以A为原点，分别以1,,ABADAA为x轴，y轴，z轴单位正向量的平面直角坐标系，写出相关的点的坐标，设出面1ADE的法向量1111(,,)nrst=.由1111,nAEnAD⊥⊥得111,,rst应满

足的方程组11110.50.50{0rsst+=−=，(1,1,1)−为其一组解，所以可取1(1,1,1)n=−.同理11ABCD的法向量2(0,1,1)n=.所以结合图形知二面角1EADB−−的余弦值为121226332nnnn==.试题解析：（Ⅰ）证明：由正方形的性质可知11///

/ABABDC，且11ABABDC==，所以四边形11ABCD为平行四边形，从而11//BCAD，又1AD面1ADE，1BC面1ADE，于是1//BC面1ADE，又1BC面11BCD，而面1AD

E面11BCDEF=，所以1//EFBC.（Ⅱ）因为四边形11AABB，11ADDA，ABCD均为正方形，所以11,,AAABAAADADAB⊥⊥⊥，且1AAABAD==，以A为原点，分别以1,,ABADAA为x轴，y轴，z轴单位正向量建立，如图所示的空间直角坐标系，可得点的坐标1

11(0,0,0),(1,0,0),(0,1,0),(0,0,1),(1,0,1),(0,1,1)ABDABD.而E点为11BD的中点，所以E点的坐标为(0.5,0.5,1).设面1ADE的法向量1111(,,)nrs

t=.而该面上向量11(0.5,0.5,0),(0,1,1)AEAD==−，由1111,nAEnAD⊥⊥得111,,rst应满足的方程组11110.50.50{0rsst+=−=，(1,1,1)−为其一组解，所以可取1(1,1,1)n=−.设面11AB

CD的法向量2222(,,)nrst=，而该面上向量111(1,0,0),(0,1,1)ABAD==−，由此同理可得2(0,1,1)n=.所以结合图形知二面角1EADB−−的余弦值为121226332nnnn==.考点：1.线面平行的判定定理与性质定理；2.二面角的求解.42．

（2015·福建·高考真题）如图，在几何体ABCDE中，四边形ABCD是矩形，AB⊥平面BEC，BEEC⊥，ABBEEC==，G，F分别是线段BE，DC的中点.(1)求证：//GF平面ADE；(2)求平面AEF与平面BEC所成锐二面角的余弦值.【答案】(1)证明见解析(2)23【分析】

（1）取AE的中点H，连接HG，HD，通过证明四边形HGFD是平行四边形来证明//GFDH，由线面平行的判定定理可得；（2）以B为原点，分别以BEBQBA，，的方向为x轴，y轴，z轴的正方向建立空间直角坐标系，可得平面BEC和平面AEF的法向量，由向量夹角的余弦值可

得．【详解】（1）如图，取AE的中点H连接HG，HD，又G是BE的中点，所以//HGAB，且12HGAB=，又F是CD中点，所以12DFCD=，由四边形ABCD是矩形得，//ABCD，ABCD=，所以//GHDF且GHDF=.从而四边形HGFD是平行四边形，所以//GFDH，∵DH平面

ADE，GF平面ADE，∴//GF平面ADE.（2）如图，在平面BEC内，过点B作//BQEC，因为BECE⊥，所以BEBQ⊥.又AB⊥平面BEC，BE，BQ平面BEC，所以ABBE⊥，ABBQ⊥.以B为原点，分别以BE，BQ，BA的方向为x轴，y

轴，z轴的正方向建立空间直角坐标系，设4AB=，则()004A,,，()0,0,0B，()4,0,0E，()4,4,2F.因为AB⊥平面BEC，所以()0,0,4BA=为平面BEC的法向量，设()nxyz=，，为平面AEF的法向量.又()404AE=−,,，()4

42AF=−,,00nAEnAF==,即4404420xzxyz−=+−=，取()212n=−,,，cosBA，242433BAnnBAn===，所以平面AEF与平面BEC所成锐二面角的余弦值

为23.【点睛】43．（2015·北京·高考真题）如图，在四棱锥AEFCB−中，AEF△为等边三角形，平面AEF⊥平面EFCB，EFBC∥，4BC=，2EFa=，60EBCFCB==，O为EF的中点．（1）求证：AOBE⊥．（

2）求二面角FAEB−−的余弦值．（3）若BE⊥平面AOC，求a的值．【答案】（1）见解析；（2）余弦为55−；（2）43a=.【详解】试题分析：（1）要证AOBE⊥，可以先证明AO垂直于BE所在的平面EFCB；（2）可以用向量法解决，取CB的

中点D，连接OD，以O为原点，分别以OEODOA、、为xyz、、轴建立空间直角坐标系，分别求出两平面AEF、平面AEB的法向量，并求出法向量的夹角的余弦值，进而得到二面角FAEB−−的余弦值；（3）因为BE⊥平面AOC，只需BEOC⊥，利用0B

EOC=即可求出a的值.试题解析：（1）由于平面AEF⊥平面EFCB，为等边三角形，O为EF的中点，则AOEF⊥，根据面面垂直性质定理，所以AO⊥平面EFCB，又BE平面EFCB，则AOBE⊥．（2）取CB的中点D，连接OD，以

O为原点，分别以OEODOA、、为xyz、、轴建立空间直角坐标系，，由于平面AEF与y轴垂直，则设平面AEF的法向量为，设平面AEB的法向量，则，二面角FAEB−−的余弦值12121215cos,55nnnnnn−=

==−，由二面角FAEB−−为钝二面角，所以二面角FAEB−−的余弦值为55−．（3）有（1）知AO⊥平面EFCB，则AOBE⊥，若BE⊥平面AOC，只需BEOC⊥，，又()()2222330BEOCaa=−−+−=，解得2a=或43a=，由于2a，则43a=．考点：1、线线垂直；2、线

面垂直；3、二面角.【思路点晴】本题是一个有关线线垂直、线面垂直、二面角方面的综合性问题，解决本题的基本思路是：对于（1）要证AOBE⊥，可以先证明AO垂直于BE所在的平面；对于（3）在建立直角坐标系之后，解决问题的关键是要正确求出平面AEF的法向量和平面AEB的法向量，之后再根据向量夹角

的公式就可求出二面角FAEB−−的余弦值；对于（3）在前两问的基础上，只需由BEOC⊥即可求出a的值.考点08已知异面直线所成角、线面角、二面角求值或范围（方程思想）1．（2024·全国新Ⅰ卷·高考真题）如图，四棱锥PABCD−中，

PA⊥底面ABCD，2PAAC==，1,3BCAB==．(1)若ADPB⊥，证明：//AD平面PBC；(2)若ADDC⊥，且二面角ACPD−−的正弦值为427，求AD．【答案】(1)证明见解析(2)3【分析】（1）先证出AD⊥平面PAB，即可得ADAB⊥，由勾股定理逆定理可得BCAB⊥，从而/

/ADBC，再根据线面平行的判定定理即可证出；（2）过点D作DEAC⊥于E，再过点E作EFCP⊥于F，连接DF，根据三垂线法可知，DFE即为二面角ACPD−−的平面角，即可求得tan6DFE=，再分

别用AD的长度表示出,DEEF，即可解方程求出AD．【详解】（1）（1）因为PA⊥平面ABCD，而AD平面ABCD，所以PAAD⊥，又ADPB⊥，PBPAP=，,PBPA平面PAB，所以AD⊥平面PAB，而AB

平面PAB，所以ADAB⊥.因为222BCABAC+=，所以BCAB⊥，根据平面知识可知//ADBC，又AD平面PBC，BC平面PBC，所以//AD平面PBC．（2）如图所示，过点D作DEAC⊥于E，再过点E作EFCP⊥于F，连接DF，因为

PA⊥平面ABCD，所以平面PAC⊥平面ABCD，而平面PAC平面ABCDAC=，所以DE⊥平面PAC，又EFCP⊥，所以⊥CP平面DEF，根据二面角的定义可知，DFE即为二面角ACPD−−的平面角，即42sin7DFE=，即tan6DFE=．

因为ADDC⊥，设ADx=，则24CDx=−，由等面积法可得，242xxDE−=，又()()222244442xxxCEx−−=−−=，而EFC为等腰直角三角形，所以2422xEF−=，故2242tan6422

xxDFEx−==−，解得3x=，即3AD=．2．（2023·全国新Ⅰ卷·高考真题）如图，在正四棱柱1111ABCDABCD−中，12,4ABAA==．点2222,,,ABCD分别在棱111,,AABBCC,1DD上，222

21,2,3AABBDDCC====．(1)证明：2222BCAD∥；(2)点P在棱1BB上，当二面角222PACD−−为150时，求2BP．【答案】(1)证明见解析；(2)1【分析】（1）建立空间直角坐标系，利用向量坐标相等证明；（2）设(

0,2,)(04)P，利用向量法求二面角，建立方程求出即可得解.【详解】（1）以C为坐标原点，1,,CDCBCC所在直线为,,xyz轴建立空间直角坐标系，如图，则2222(0,0,0),(0,0,3),(0,2,2),(2,0,2),(2,2,1

)CCBDA，2222(0,2,1),(0,2,1)BCAD=−=−，2222BCAD∥，又2222BCAD，不在同一条直线上，2222BCAD∥.（2）设(0,2,)(04)P，则2222

2(2,2,2)(0,2,3),=(2,0,1),ACPCDC=−−=−−−，设平面22PAC的法向量(,,)nxyz=，则22222202(3)0nACxyznPCyz=−−+==−+−=，令2z=，得

3,1yx=−=−，(1,3,2)n=−−，设平面222ACD的法向量(,,)mabc=，则2222222020mACabcmDCac=−−+==−+=，令1a=，得1,2==bc，(1,1,2)m

=，2263cos,cos150264(1)(3)nmnmnm====+−+−，化简可得，2430−+=，解得1=或3=，(0,2,1)P或(0,2,3)P，21BP=.3．（2021·全国新Ⅰ卷·高考真题）如图，在三棱锥ABCD−中，平面ABD⊥平面BCD，

ABAD=，O为BD的中点.（1）证明：OACD⊥；（2）若OCD是边长为1的等边三角形，点E在棱AD上，2DEEA=，且二面角EBCD−−的大小为45，求三棱锥ABCD−的体积.【答案】(1)证明见解析；(2)36.【分析】(1)由题意首先证得线面垂直，然后利用线面垂直的定义证

明线线垂直即可；(2)方法二：利用几何关系找到二面角的平面角，然后结合相关的几何特征计算三棱锥的体积即可.【详解】（1）因为ABAD=，O是BD中点，所以OABD⊥，因为OA平面ABD，平面ABD⊥平面BCD，且平面ABD

平面BCDBD=，所以OA⊥平面BCD．因为CD平面BCD，所以OACD⊥.（2）[方法一]：通性通法—坐标法如图所示，以O为坐标原点，OA为z轴，OD为y轴，垂直OD且过O的直线为x轴，建立空间直角坐标系Oxyz−，则31(,,0),(0

,1,0),(0,1,0)22CDB−，设12(0,0,),(0,,)33AmEm,所以4233(0,,),(,,0)3322EBmBC=−−=，设(),,nxyz=r为平面EBC的法向量，则由00EBnBCn

==可求得平面EBC的一个法向量为2(3,1,)nm=−−．又平面BCD的一个法向量为()0,0,OAm=，所以222cos,244nOAmm−==+，解得1m=．又点C到平面ABD的距离为32，所以1133213226ABCDCA

BDVV−−===，所以三棱锥ABCD−的体积为36．[方法二]【最优解】：作出二面角的平面角如图所示，作EGBD⊥，垂足为点G．作GFBC⊥，垂足为点F，连结EF，则OAEG∥．因为OA⊥平面BCD，所以EG⊥平面BCD

，EFG为二面角EBCD−−的平面角．因为45EFG=，所以EGFG=．由已知得1OBOD==，故1OBOC==．又30OBCOCB==，所以3BC=．因为24222,,,,133333GDGBFGCDEGOA====

==，11113322(11)1333226ABCDBCDBOCVSOSOAA−====．[方法三]：三面角公式考虑三面角BEDC−，记EBD为，EBC为，30DBC=，

记二面角EBCD−−为．据题意，得45=．对使用三面角的余弦公式，可得coscoscos30=，化简可得3coscos2=．①使用三面角的正弦公式，可得sinsinsin=，化

简可得sin2sin=．②将①②两式平方后相加，可得223cos2sin14+=，由此得221sincos4=，从而可得1tan2=．如图可知π(0,)2，即有1tan2=，根据三角形相似知，点G为OD的三等分点，即

可得43BG=，结合的正切值，可得2,13EGOA==从而可得三棱锥ABCD−的体积为36．【整体点评】(2)方法一：建立空间直角坐标系是解析几何中常用的方法，是此类题的通性通法，其好处在于将几何问题代数化，适合

于复杂图形的处理；方法二：找到二面角的平面角是立体几何的基本功，在找出二面角的同时可以对几何体的几何特征有更加深刻的认识，该法为本题的最优解.方法三：三面角公式是一个优美的公式，在很多题目的解析中灵活使用三面角公式可

以使得问题更加简单、直观、迅速.4．（2021·北京·高考真题）如图：在正方体1111ABCDABCD−中，E为11AD中点，11BC与平面CDE交于点F．（1）求证：F为11BC的中点；（2）点M是棱11AB上一点，且二面角MFCE−−的余弦值为53，求111AMAB的值．【答案】（

1）证明见解析；（2）11112AMAB=．【分析】(1)首先将平面CDE进行扩展，然后结合所得的平面与直线11BC的交点即可证得题中的结论；(2)建立空间直角坐标系，利用空间直角坐标系求得相应平面的法向量，然后解方程即可求得

实数的值.【详解】(1)如图所示，取11BC的中点F'，连结,','DEEFFC，由于1111ABCDABCD−为正方体，,'EF为中点，故'EFCDP，从而,',,EFCD四点共面，即平面CDE即平面'CDEF，据此可得：直线11BC交平面CDE于点F'，当直线与平面

相交时只有唯一的交点，故点F与点F'重合，即点F为11BC中点.(2)以点D为坐标原点，1,,DADCDD方向分别为x轴，y轴，z轴正方向，建立空间直角坐标系Dxyz−，不妨设正方体的棱长为2，设()11101AMAB=，则：()()()()2,2,2,0,2

,0,1,2,2,1,0,2MCFE，从而：()()()2,22,2,1,0,2,0,2,0MCCFFE=−−−==−，设平面MCF的法向量为：()111,,mxyz=，则：()111112222020mMCxyzmCFxz=−+−−==+=，令11z=−可得：12,,

11m=−−，设平面CFE的法向量为：()222,,nxyz=，则：2222020nFEynCFxz=−==+=，令11z=−可得：()2,0,1n=−，从而：215,5,51

mnmn==+=−，则：2,155155cos3mnmnmn+−===，整理可得：()2114−=，故12=（32=舍去）.【点睛】本题考查了立体几何中的线面关系和二面角的求解问题，意在考查学生的空间想象能力和

逻辑推理能力，对于立体几何中角的计算问题，往往可以利用空间向量法，通过求解平面的法向量，利用向量的夹角公式求解.5．（2017·天津·高考真题）如图，在三棱锥−PABC中，PA⊥底面ABC，90BAC=．点D，E，N分别为棱PA，PC

，BC的中点，M是线段AD的中点，4PAAC==，2AB=．（1）求证：MN∥平面BDE；（2）求二面角CEMN−−的正弦值；（3）已知点H在棱PA上，且直线NH与直线BE所成角的余弦值为721，求线段AH的长．【答案】（1）证明见解析；（2）10521；（3）8

5或12．【详解】试题分析：本小题主要考查直线与平面平行、二面角、异面直线所成的角等基础知识.考查用空间向量解决立体几何问题的方法.考查空间想象能力、运算求解能力和推理论证能力.首先要建立空间直角坐标系，写出相关点的坐标，证明

线面平行只需求出平面的法向量，计算直线对应的向量与法向量的数量积为0，求二面角只需求出两个半平面对应的法向量，借助法向量的夹角求二面角，利用向量的夹角公式，求出异面直线所成角的余弦值，利用已知条件，求出A

H的值.试题解析：如图，以A为原点，分别以AB，AC，AP方向为x轴、y轴、z轴正方向建立空间直角坐标系.依题意可得A（0，0，0），B（2，0，0），C（0，4，0），P（0，0，4），D（0，0，2）

，E（0，2，2），M（0，0，1），N（1，2，0）.（1）证明：DE=（0，2，0），DB=（2，0，2−）.设(),,nxyz=，为平面BDE的法向量，则00nDEnDB==，即20220yxz=−=.不妨设1z=，可得()1,0,1n=.又MN=（1，2，1−），

可得0MNn=.因为MN平面BDE，所以MN//平面BDE.（2）解：易知()11,0,0n=ur为平面CEM的一个法向量.设()2,,nxyz=为平面EMN的法向量，则2200nEMnMN==，因为(

)0,2,1EM=−−，()1,2,1MN=−，所以2020yzxyz−−=+−=.不妨设1y=，可得()24,1,2n=−−.因此有1212124,21nncosnnnn==−，于是12105sin,21nn=.所以

，二面角C—EM—N的正弦值为10521.（3）解：依题意，设AH=h（04h），则H（0，0，h），进而可得()1,2,NHh=−−，()2,2,2BE=−.由已知，得2227cos,21523NH

BEhNHBENHBEh−===+，整理得2102180hh−+=，解得85h=，或12h=.所以，线段AH的长为85或12.【考点】直线与平面平行、二面角、异面直线所成的角【名师点睛】空间向量是解决空间几何问题的锐利武器，

不论是求空间角、空间距离还是证明线面关系利用空间向量都很方便，利用向量夹角公式求异面直线所成的角又快又准，特别是借助平面的法向量求线面角，二面角或点到平面的距离都很容易.6．（2017·全国·高考真题）如图，四棱锥P-ABCD中，侧面PAD是边长为2的等边三角形且垂直于底

面ABCD，o1,90,2ABBCADBADABC====E是PD的中点．（1）证明：直线//CE平面PAB；（2）点M在棱PC上，且直线BM与底面ABCD所成角为o45，求二面角MABD−−的余弦值．【答案】（1）见解析；（2）1

05【详解】试题分析：（1）取PA的中点F，连结EF，BF，由题意证得CE∥BF，利用线面平行的判断定理即可证得结论；（2）建立空间直角坐标系，求得半平面的法向量：(0,6,2)m=−，()0,0,1

n=，然后利用空间向量的相关结论可求得二面角MABD−−的余弦值为105．试题解析：（1）取PA中点F，连结EF，BF．因为E为PD的中点，所以//EFAD,12EFAD=,由90BADABC==得//BCAD，又12BCAD=所以．四边形BCEF为平行四边形，//CEBF．又B

FPAB平面，CEPAB平面，故//CEPAB平面（2）由已知得BAAD⊥,以A为坐标原点，AB的方向为x轴正方向，AB为单位长，建立如图所示的空间直角坐标系A-xyz,则则()000A，，，()100B，，，()110C，，，()013P，，，()1

03PC=−，，,()100AB，，=则()()1,13BMxyzPMxyz=−=−−，，，，因为BM与底面ABCD所成的角为45°，而()001n=，，是底面ABCD的法向量，所以0,cossin45BMn=，()222z221xyz=−++即（x-1）²+y²-z²=0又M在棱PC上

,设,PMPC=则x,1,33yz===−由①，②得()22x=1+x=1-22y=1y=166zz22=−=舍去，所以M261-,1，22，从而26AM1-,122=，设()000x,y,zm=是平面ABM的法向

量，则()00002-2x2y6z0·AM0·AB0x0mm++====即所以可取(0,6,2)m=−.于是·10,5mncosmnmn==因此二面角M-AB-D的余弦值为105点睛:（1）求解

本题要注意两点：①两平面的法向量的夹角不一定是所求的二面角，②利用方程思想进行向量运算，要认真细心、准确计算．（2）设m，n分别为平面α，β的法向量，则二面角θ与<m，n>互补或相等，故有|cosθ|＝|cos<m，n>|=·mnmn

．求解时一定要注意结合实际图形判断所求角是锐角还是钝角．7．（2015·天津·高考真题）如图，在四棱柱1111ABCDABCD−中，侧棱1AA⊥底面ABCD，ABAC⊥，1AB=，12ACAA==，5ADCD==，且点M和N分别为1BC和

1DD的中点.（1）求证：//MN平面ABCD；（2）求二面角11DACB−−的正弦值；（3）设E为棱11AB上的点，若直线NE和平面ABCD所成角的正弦值为13，求线段1AE的长.【答案】（1）证明见解析；（2）31010；（3）72−【详解】如图，以A为原点建立空间直角坐标系，

依题意可得(0,0,0),(0,1,0),(2,0,0),(1,2,0)ABCD−，又因为,MN分别为1BC和1DD的中点，得11,,1,(1,2,1)2MN−.（Ⅰ）证明：依题意，可得(0,0

,1)n=为平面ABCD的一个法向量，50,,02MN=−，由此可得，0MNn=，又因为直线MN平面ABCD，所以//MN平面ABCD（Ⅱ），设1(,,)nxyz=为平面1ACD的法向量，则1110{0nADnAC==，即220{2

0xyzx−+==，不妨设1z=，可得1(0,1,1)n=ur，设2(,,)nxyz=为平面1ACB的一个法向量，则2120{0nABnAC==，又1(0,1,2)AB=，得20{20yzx+==，不妨设1z=，可得2(0,2,1)n=−因此有12121210cos,10n

nnnnn==−，于是12310,10sinnn=，所以二面角11DACB−−的正弦值为31010.（Ⅲ）依题意，可设111AEAB=，其中[0,1]，则(0,,2)E，从而(1,2,1)NE=−+，又(0,0,1)n=为平面A

BCD的一个法向量，由已知得22211cos,3(1)(2)1NEnNEnNEn===−+++，整理得2430+−=，又因为[0,1]，解得72=−，所以线段1AE的长为72−.考点：直线和平面平行和垂直的判定与性质，二面角、直线与平面所成的角，空间向量的应用.8．（2

015·湖南·高考真题）如图，直三棱柱111ABCABC-的底面是边长为2的正三角形，,EF分别是1,BCCC的中点．（１）证明：平面AEF⊥平面11BBCC；（２）若直线1AC与平面11AABB所成的角为45，求三棱锥

FAEC−的体积．【答案】（Ⅰ）见解析；（Ⅱ）612.【详解】试题分析：（１）由面面垂直的判定定理很容易得结论；（２）所求三棱锥底面积容易求得，是本题转化为求三棱锥的高FC，利用直线1AC与平面11AABB所成的角为，作出线面角，进而可求得的值，则可得的FC长．

试题解析：（1）如图，因为三棱柱111ABCABC-是直三棱柱，所以1⊥，又是正三角形C的边C的中点，所以C⊥又1C=，因此⊥平面11CC而平面F，所以平面F⊥平面11CC（2）设的中点为D，连结1D

,CD因为C是正三角形，所以CD⊥又三棱柱111ABCABC-是直三棱柱，所以1CD⊥因此CD⊥平面11，于是1CD为直线1C与平面11所成的角，由题设，1CD45=，所以13DCD32===在1RtD中，2211DD312=−=−

=，所以112FC22==故三棱锥FC−的体积C11326VFC332212S===考点：直线与平面垂直的判定定理；直线与平面所成的角；几何体的体积．9．（2015·湖南·高考真题）如

图，已知四棱台1111ABCDABCD−的上、下底面分别是边长为3和6的正方形，16AA=，且1AA⊥底面ABCD，点,PQ分别在棱1,DDBC上．（1）若P是1DD的中点，证明：1ABPQ⊥；（2）若//PQ平面11ABBA，二

面角PQDA−−的余弦值为37，求四面体ADPQ的体积．【答案】（1）见解析（2）24V=【详解】根据已知条件知AB，AD，1AA三直线两两垂直，所以分别以这三直线为x，y，z轴，建立如图所示空间直角

坐标系，则：(0A，0，0)，(6B，0，0)，(0D，6，0)，1(0A，0，6)，1(3B，0，6)，1(0D，3，6)；Q在棱BC上，设(6Q，1y，0)，106y剟；（1）证明：若P是1DD的中点，则9(0,,3)2P；19(6,,3)

2PQy=−−，1(3,0,6)AB=；10ABPQ=；1ABPQ⊥；1ABPQ⊥；（2）设(0P，2y，2)z，2y，2[0z，6]，P在棱1DD上；1DPDD=，01剟；(0，26y−，2)(0z=，3−，6)；22636yz−=−=；22122zy=−；

(0P，2y，2122)y−；122(6,,212)PQyyy=−−；平面11ABBA的一个法向量为(0,6,0)AD=；//PQ平面11ABBA；126()0PQADyy=−=；12yy=；(6Q，2y，0)；设平面PQD的法向量为(,

,)nxyz=，则：226(212)06(6)0nPQxyznDQxyy=+−==+−=；2632yxzyz−==，取1z=，则26(,2,1)3yn−=；又平面AQD的一个法向量为1(0,0,6)AA=；又二面角PQDA−−的余弦值为37；12263cos,7

66()53nAAy==−+；解得24y=，或28y=（舍去）；(0P，4，4)；三棱锥PADQ−的高为4，且166182ADQS==；1184243ADPQPADQVV−===四面体三棱锥．考点：1.空间向量的运用；2.线面垂直的性质；3.空间几何体体积计算.【名师点睛】

本题主要考查了线面垂直的性质以及空间几何体体积计算，属于中档题，由于空间向量工具的引入，使得立体几何问题除了常规的几何法之外，还可以考虑利用向量工具来解决，因此有关立体几何的问题，可以建立空间直角坐标系，借助于向量知识来解决，在立体几何的线面关

系中，中点是经常使用的一个特殊点，无论是试题本身的已知条件，还是在具体的解题中，通过找“中点”，连“中点”，即可出现平行线而线线平行是平行关系的根本，在垂直关系的证明中线线垂直是核心，也可以根据已知的平面图形通过计算的方式证明线线垂直，也可以根据已知

的垂直关系证明线线垂直.10．（2015·湖北·高考真题）《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖臑．如图，在阳马PABCD−中，侧棱PD⊥底面ABCD，且PDCD=，过棱PC的中点E，作EFPB

⊥交PB于点F，连接,,,.DEDFBDBE（Ⅰ）证明：PBDEF⊥平面．试判断四面体DBEF是否为鳖臑，若是，写出其每个面的直角（只需写出结论）；若不是，说明理由；（Ⅱ）若面DEF与面ABCD所成二面角

的大小为π3，求DCBC的值．【答案】（Ⅰ）详见解析；（Ⅱ）．【详解】（解法1）（Ⅰ）因为PD⊥底面ABCD，所以PDBC⊥，由底面ABCD为长方形，有BCCD⊥，而PDCDD=，所以．而DEPCD平面，所以BCDE⊥．又因为PDCD=，点E是PC的中点，所以DEPC⊥．而PCBCC=，

所以DE⊥平面PBC．而PBPBC平面，所以PBDE⊥．又PBEF⊥，DEEFE=，所以PB⊥平面DEF．由DE⊥平面PBC，PB⊥平面DEF，可知四面体BDEF的四个面都是直角三角形，即四面体BDEF是一个鳖臑，其四个面的直角分别为DEBDEF

，，EFBDFB，．（Ⅱ）如图1，在面PBC内，延长BC与FE交于点G，则DG是平面DEF与平面ABCD的交线．由（Ⅰ）知，PBDEF⊥平面，所以PBDG⊥．又因为PD⊥底面ABCD，所以PDDG⊥．而PDPBP=，所以DGPBD⊥平面．故BDF是面DEF与面ABCD所成二面角的平面角，

设1PDDC==，BC=，有21BD=+，在Rt△PDB中,由DFPB⊥,得π3DPFFDB==,则2πtantan133BDDPFPD===+=,解得2=．所以12.2DCBC==故当面DEF与面ABCD所成二面角的大小为π3时，22DC

BC=．（解法2）（Ⅰ）如图2，以D为原点，射线,,DADCDP分别为,,xyz轴的正半轴，建立空间直角坐标系．设1PDDC==，BC=，则(0,0,0),(0,0,1),(,1,0),(0,1,0)DPBC，(,1,1)PB=−，点E是PC的中

点，所以11(0,,)22E，，于是0PBDE=，即PBDE⊥．又已知EFPB⊥，而DEEFE=，所以PBDEF⊥平面．因,0DEPC=,则DEPC⊥,所以．由DE⊥平面PBC，PB⊥平面DEF，可知四面体BD

EF的四个面都是直角三角形，即四面体BDEF是一个鳖臑，其四个面的直角分别为DEBDEF，，EFBDFB，．（Ⅱ）由PDABCD⊥平面，所以是平面ABCD的一个法向量；由（Ⅰ）知，PBDEF⊥

平面，所以是平面DEF的一个法向量．若面DEF与面ABCD所成二面角的大小为π3，则2π11cos322BPDPBPDP===+，解得2=．所以12.2DCBC==故当面DEF与面ABCD所成

二面角的大小为π3时，22DCBC=．考点：四棱锥的性质，线、面垂直的性质与判定，二面角．