【文档说明】广东省清远市2021-2022学年高二下学期期末质量检测 数学含答案.docx，共(12)页，716.617 KB，由小赞的店铺上传

转载请保留链接：https://www.doc5u.com/view-f2f39ed66c1abf0ffab53dce42a31a14.html

以下为本文档部分文字说明：

-1-清远市2021~2022学年第二学期高中期末质量检测高二数学一､选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.从甲地出发前往乙地，一天中有4趟汽车、3趟火车和1趟航班

可供选择．某人某天要从甲地出发，去乙地旅游，则所有不同走法的种数是（）A.16B.15C.12D.8【答案】D2.下列求导运算正确的是（）A.2111xxx+=+B.()1[ln4]xx=C.222xxxxxee+=D.()22cos2cossinxxxxxx

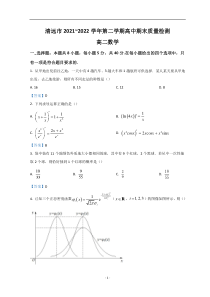
=+【答案】B3.袋中装有11个除颜色外质地大小都相同的球，其中有9个红球，2个黑球．若从中一次性抽取2个球，则恰好抽到1个红球的概率是（）A.1033B.955C.29D.1855【答案】D4.已知三个正态密度函数()()2221e2iixiix

−−=（xR，1,2,3i=）的图像如图所示，则（）-2-A.132=，123=B.123=，123C.132=，123=D.123=，123=【答案】C5.回文联是我国对联中的一种，它是用回文形式写成的对

联，既可顺读，也可倒读，不仅意思不变，而且颇具趣味．相传，清代北京城里有一家饭馆叫“天然居”，曾有一副有名的回文联：“客上天然居，居然天上客；人过大佛寺，寺佛大过人．”在数学中也有这样一类顺读与倒读都是同一个数的正整数，被称为“回文数

”，如22，575，1661等．那么用数字1，2，3，4，5可以组成4位“回文数”的个数为（）A.25B.20C.30D.36【答案】A6.已知随机变量()~4,XBp，若()()209EXDX+=，则()1PX=（）A.1681B.6581C.8

9D.49【答案】B7.已知函数()ln2fxaxx=+在)1,+上单调递增，则实数a的最小值为（）A.2−B.2C.1−D.1【答案】A8.函数()fx的导函数是()fx¢，下图所示的是函数()()()1Ryxfxx=+的图像，下列说法正确的是（）A.1x=−是(

)fx的零点B.2x=是()fx的极大值点-3-C.()fx在区间()2,1−−上单调递增D.()fx在区间2,2−上不存在极小值【答案】B二､多选题：本题共4小题，每小题5分，共20分.在每小题给出

的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.9.对具有线性相关关系的变量,xy有一组观测数据()(),1,2,3,,10iixyi=，已知10120iix==，10110iiy==，

则（）A.数据()211,2,3,,10iixyi−+=的平均数为0B.若变量,xy的经验回归方程为ˆˆ2yxa=+，则实数ˆ3a=−C.变量,xy的样本相关系数r越大，表示模型与成对数据,xy的线性相关性越强D.变量,xy

的决定系数2R越大，表示模型与成对数据,xy拟合的效果越好【答案】BD10.已知()32nx+展开式中的二项式系数和为32，若()201232nnnxaaxaxax+=++++，则（）A.n＝5B.032a=C.3270a=D.()01

2311nnaaaaa−+−++−=−【答案】ABD11.现分配甲、乙、丙三名临床医学检验专家到A，B，C，D，E五家医院进行核酸检测指导，每名专家只能选择一家医院，且允许多人选择同一家医院，则（）A.所有可能的安排方法有125种B.若A医院必须有专家去

，则不同的安排方法有61种C.若专家甲必须去A医院，则不同的安排方法有16种D.若三名专家所选医院各不相同，则不同的安排方法有10种-4-【答案】AB12.已知函数()e2xfxx=+−和()ln2gxxx=+−，若()()120fxgx==，则

（）A.122xx+=B.1102xC.12exxD.1221lnlnxxxx−【答案】ABD三､填空题：本题共4小题，每小题5分，共20分，把答案填在答题卡中的横线上.13.()412xx−展开式中的常数项为________．【答案】2414.函数()32

2fxxxx=−+的图象在点()()1,1f处的切线方程为___________.【答案】2yx=15.某学校高一､高二､高三的学生人数之比为5:5:6，这三个年级分别有20%,30%,20%的学生获得过奖学金，现随机选取一名学生，此学生恰好获得过奖

学金，则该学生是高二年级学生的概率为___________.【答案】153716.为了检测自动流水线生产的食盐质量，检验员每天从生产线上随机抽取()*kkN包食盐，并测量其质量（单位：g）.由于存在各种不可控制的因素，任意抽取的一包食盐的质量与标准质量之间存在一定的误差.已知这条生产

线在正常状态下，每包食盐的质量服从正态分布()2,N.假设生产状态正常，记X表示每天抽取的k包食盐中质量在()3,3−+之外的包数，若X的数学期望()0.03EX，则k的最小值为___________.

附：若随机变量X服从正态分布()2,N，则(33)0.9973PX−+.-5-【答案】12四､解答题：本题共6小题，共70分.解答应写出文字说明､证明过程或演算步骤.17.在①()sincos6aACbA+=−，②coscos2A

aCbc=−，③()()()()sinsinsinbcABbaAB−+=−+这三个条件中任选一个，补充在下面的问题中并解答.问题：在ABC中，内角,,ABC的对边分别为,,abc，且满足___________.（1

）求角A；（2）若3,5abc=+=，求ABC的面积.注：如果选择多个条件分别解答，按第一个解答计分.【答案】（1）3（2）43318.已知数列na的前n项和nS满足22nSnn=+，数列2lognb是公差为1−的等差数列，11b=.（1）求数列,nnab的通项

公式；（2）设111nnnncbaa++=+，求数列nc的前n项和nT.【答案】（1）nan=，112nnb−=（2）11212nnTn=−−+19.为提升学生的身体素质，某地区对体育测试选拔赛试行改革．在高二一学年中举行4次全区选拔赛

，学生如果在4次选拔赛中有2次成绩达到全区前20名即可取得体育特长生资格，不用参加剩余的比赛．规定：每个学生最多只能参加4次选拔比赛，若前3次选拔赛成绩都没有达到-6-全区前20名，则不能参加第4次选

拔赛．（1）若该赛区某次选拔赛高二年级共有500名学生参加，统计出的参赛学生中男、女生成绩如下表：前20名人数第21至第500名人数合计男生15300女生195合计20500请完成上述2×2列联表，并判断是否有90%的把握认为选拔赛成绩与性别有关．（2）假设某学生每次成绩达到全区前20名的概率都是

13，每次选拔赛成绩能否达到全区前20名相互独立．如果该学生参加本年度的选拔赛（规则内不放弃比赛），记该学生参加选拔赛的次数为，求的分布列及数学期望．参考公式及数据：()()()()()22nadbcabcdacb

d−=++++，其中nabcd=+++．a0.150.100.050.01002.0722.7063.8416.635【答案】（1）填表见解析；没有（2）分布列见解析；期望为103【小问1详解】列联表如下：前20名人数第21至第500名人数合

计男生15285300女生5195200合计20480500零假设为-7-0H：选拔赛成绩与性别无关．根据列联表，得()()()()()()2225001519552851.9532.70630020020480nadbcabcdacbd−−==++++，所以没

有90%的把握认为选拔赛成绩与性别有关．【小问2详解】该学生参加选拔赛次数的可能取值为2，3，4．()211239P===，()312121243C33339P==+=，()()()

14441231999PPP==−=−==−−=．故的分布列为234P194949()144102349993E=++=．20.如图，在三棱锥PABC−中，PA⊥平面ABC，点,MN分别是,PBAC的中点，且MNAC⊥.（1）证

明：BC⊥平面PAC.（2）若4,22PAACBC===，求平面PBC与平面AMC夹角的余弦值.-8-【答案】（1）证明见解析；（2）13.【小问1详解】由PA⊥平面ABC，BC平面ABC，则PABC⊥.又MNAC⊥

，点N为AC的中点，所以MAMC=.由,PAABM⊥为PB的中点，则12MAPB=，即12PBMC=，所以2PCB=，即BCPC⊥，又PAPCP=，,PAPC面PAC，所以BC⊥平面PAC.【小问2详解】由（1）得：B

CAC⊥，以点C为坐标原点，以,CBCA为x轴，y轴的正方向，以AP为z轴的正方向建立空间直角坐标系Cxyz−.因为4,22PAACBC===，所以()()()()0,22,0,0,22,4,22,0,0,2,2,2APBM，故(0,22,4)CP=，(22,0,0)CB

=，(0,22,0)CA=，(2,2,2)CM=，设平面PBC的法向量为(),,mxyz=，则2240220CPmyzCBmx=+===，令1z=，故()0,2,1m=−.设平面AMC的法向量为(),,nabc=

，则220{2220CAnbCMnabc===++=，令1c=，故()2,0,1n=−，所以平面PBC与平面AMC夹角的余弦值为11cos333mnmn===.-9-21.已知椭圆2222:1(0)xyCabab+=的一个焦点与短轴的一个端点连线的倾斜角为

30，直线12y=与椭圆C相交于P和Q两点，且23,PQO=为坐标原点.（1）求椭圆C的方程；（2）直线l与椭圆C交于,AB两点，直线OA的斜率为1k，直线OB的斜率为2k，且1214kk=−，求OAOB的取值范围.【答案】（1）2214

xy+=（2）33,00,22−22.已知函数()12lnfxxaxx=−+，()ecos2xgxxx=+−−．（1）当01a时，讨论()fx的单调性；（2）设m，n为正数，且当1a=时，()()fmgn=，证明：()21eln2nfgm−−

．【答案】（1）答案见解析（2）证明见解析【小问1详解】()12lnfxxaxx=−+的定义域为()0,+，-10-()()2222121axxfxaxxx−−+=−−=（0x）．①当0a=时，()221xfxx−=，令()0fx¢<，得102x；令()0fx¢>，得12x．

所以()fx在10,2上单调递减，在1,2+上单调递增．②当01a时，因为2210axx−+=的判别式440a=−，所以2210axx−+=有两正根111axa−−=，21

1axa+−=，且12xx．令()0fx¢<，得110axa−−或11axx+−；令()0fx¢>，得1111aaxxx−−+−．所以()fx在110,aa−−和11,aa+−+上单调递减，在1111,−−+−aaaa上单调递增．综

上，当0a=时，()fx在10,2上单调递减，在1,2+上单调递增；当01a时，()fx在110,aa−−和11,aa+−+上单调递减，在1111,−−+−aaaa上单调递增;【

小问2详解】证明：因为1a=，所以()12lnfxxxx=−+（0x）．设()()()22222e4eeecos2ee3ecos2xxxxxxxhxfgxxxxxx−−−=−=−−+−−++=−−−−+，则()

222e2ee3sinxxxhxx−+−+=−．当0x时，因为2eexx，20e1x−，令()()222e2ee3sinxxxtxhxx−==+−−+，-11-则()()2222224e4eecos3eeecos4e3ecos4xxxxxxxxtxxxx−−

=−−+=+−+−+−．令()23ecos4xxx=+−，因为0x，则()26esin0xxx−=，所以()x在()0,+上单调递增，又()00=，所以()0x，则()0tx，所以()hx在()0,+上

单调递增，又()00h=，所以()0hx，则()hx在()0,+上单调递增．又()00h=，所以()0hx，则()()2e0xfgx−−．因为0m，0n，所以()()()2enfgnfm

−=．又()()2212110xfxxxx−=−−=−，所以()fx在()0,+上单调递减，所以2enm−，整理得1ln2nm−．又当0x时，令()()esin1xpxgxx==−−，则()ecos0xpxx=−，所以()gx在()0,+上单调递增，()(

)00gxg=，则()gx在()0,+上单调递增，所以()1ln2gngm−．故()21eln2nfgm−−．12获得更多资源请扫码加入享学资源网微信公众号www.xiangxue100.com