【文档说明】新人教版高中数学教材例题课后习题 必修一 4．2 指数函数 Word版含解析.docx，共(14)页，534.419 KB，由小赞的店铺上传

转载请保留链接：https://www.doc5u.com/view-cc9484971fe6064525daa2ded54ce97a.html

以下为本文档部分文字说明：

第四章指数函数与对数函数4.2指数函数例1已知指数函数()xfxa=（0a，且1a），且(3)πf=，求(0)f，(1)f，(3)f−的值.分析：要求(0)f，(1)f，(3)f−的值，应先求出()xfxa=的解析式，即先求a的值.解：因为()xfxa=，且(3)πf=，则3πa=，

解得13πa=，于是3()πxfx=.所以，0(0)π1f==，133(1)ππf==，11(3)ππf−−==.例2（1）在问题1中，如果平均每位游客出游一次可给当地带来1000元门票之外的收入，A地景区的门票价格为150元，比较这15年间A，B两地旅游收入变化情况.（2）在问题2中

，某生物死亡10000年后，它体内碳14的含量衰减为原来的百分之几？解：（1）设经过x年，游客给A，B两地带来的收入分别为()fx和()gx，则()1150(10600)fxx=+，()10002781.11xgx=.利用计算工具可得，当0x=时，(0)(0)412000fg−=

.当10.22x时，(10.22)(10.22)fg.结合图可知：当10.22x时，()()fxgx，当10.22x时，()()fxgx.当14x=时，(14)(14)347303gf−.这说明，在2001年，游客给A地带来的收入比B地多412000万元；随后10年，虽然()(

)fxgx，但()gx的增长速度大于()fx；根据上述数据，并考虑到实际情况，在2011年2月某个时刻就有()()fxgx=，这时游客给A地带来的收入和B地差不多；此后，()()fxgx，游客给B地带来的收入超过了A地；由于()gx增长得越

来越快，在2015年，B地的收入已经比A地多347303万元了.（2）设生物死亡x年后，它体内碳14含量为()hx.如果把刚死亡的生物体内碳14含量看成1个单位，那么157301()2xhx=

.当10000x=时，利用计算工具求得1000057301(10000)0.302h=.所以，生物死亡10000年后，它体内碳14含量衰减为原来的约30%.例3比较下列各题中两个值的大小：（1）2.51.7，31.7；（2）20.8−，30.8−；（3）0.

31.7，3.10.9.分析：对于（1）（2），要比较两个值可以看作一个指数函数的两个函数值，因此可以直接利用指数函数的单调性进行比较；对于（3），0.31.7和3.10.9不能看作某一个指数函数的两个函数值.

可以利用函数1.7xy=和0.9xy=的单调性，以及“0x=时，1y=”这条性质把它们联系起来.解：（1）2.51.7和31.7可看作函数1.7xy=当x分别取2.5和3时所对应的两个函数值.因为底数1.71

，所以指数函数1.7xy=是增函数.的因为2.53，所以2.531.71.7.（2）同（1）理，因为00.81，所以指数函数0.8xy=是减函数.因23−−，所以230.80.8−−.（3）由指数函数的性质知0.301.71.71=，3.100.90

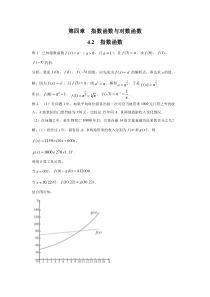
.91=，所以0.33.11.70.9.例4如图，某城市人口呈指数增长.（1）根据图象，估计该城市人口每翻一番所需的时间（倍增期）；（2）该城市人口从80万人开始，经过20年会增长到多少万人？分析：（1）因为该城市人口呈指数增长，而同一指数函

数的倍增期是相同的，所以可以从图象中选取适当的点计算倍增期.（2）要计算20年后的人口数，关键是要找到20年与倍增期的数量关系.解：（1）观察图，发现该城市人口经过20年约为10万人，经过40年约为20万人，即由10万人口增加到2

0万人口所用的时间约为20年，所以该城市人口每翻一番所需的时间约为20年.（2）因为倍增期为20年，所以每经过20年，人口将翻一番.因此，从80万人开始，经过20年，该城市人口大约会增长到160万人.4.2.1指数函数的概念练习为1.下列图象中，有可能表示指数函数的是（）A.B.C.D.【答案】C

【解析】【分析】根据指数函数的图象与性质选择．【详解】由于0xya=（0a，且1a），所以A，B，D都不正确，故选C.【点睛】本题考查指数函数的图象与性质，属于基础题．如指数函数图象恒过点(0,1)，值域是(0,)+．2.已知函数(),yfxx=R

，且(0.5)(1)(0.5)(0)3,2,2,,2(0)(0.5)(0.5(1))fffnffffn====−，*nN，求函数()yfx=的一个解析式.【答案】()34xfx=【解析】【分析】用连乘法求(1),(2),(3)fff，然后用归纳法归纳一个结

论．【详解】由己知得，(1)(0.5)(1)4(0)(0)(0.5)ffffff==，2(2)(0.5)(1)(1.5)(2)4(0)(0)(0.5)(1)(1.5)ffffffffff==，3(3)(0.5)(1)(1.5)(2)(2.5)(3)4(0)(0)(0.5)(1)(1.

5)(2)(2.5)ffffffffffffff==，()4(0)xfxf=，又(0)3,()34xffx==.【点睛】本题考查指数函数的解析式，由于只知道一些函数值，并不知道函数的形式，因此可用归纳法思想归纳一个结论．3.在某个时期，某

湖泊中的蓝藻每天以6.25%的增长率呈指数增长，那么经过30天，该湖泊的蓝藻会变为原来的多少倍？（可以使用计算工具）【答案】6.16倍【解析】【分析】根据平均增长率问题可得．【详解】设现在的蓝藻量为a，经过30天后的蓝藻量为y，则30(16.25%)ya

=+，301.06256.16ya=，∴经过30天，该湖泊的蓝藻会变为原来的6.16倍.【点睛】本题考查平均增长率问题，平均增长率问题的函数模型是(1%)xyap=+．4.2.2指数函数的图象和性质练习4.在同一直角坐标系中画出函数3xy=和13xy=的图象，并说明

它们的关系.【答案】见解析【解析】【分析】根据指数函数图象与性质作图，由图观察对称性．【详解】3xy=和13xy=的图象如图，3xy=和13xy=的图象关于y轴对称【点睛】本题考查指数函数的图象，属于基础题．5.比较下列各题中两个值的大小：（1）2

26,7；（2）3.52.30.3,0.3−−；（3）0.51.21.2,0.5.【答案】（1）；（2）；（3）【解析】【分析】（1）由函数2yx=的单调性比较；（2）由函数0.3xy=的单调性比较；（3）与

中间值1比较．【详解】（1）函数2yx=在(0,)+上是增函数，22067,67.（2）函数0.3xy=在R上为减函数，3.52.33.52.3,0.30.3−−−−.（3）0.501.200.51.21.21.21;0.50.51,1.20.5==.【点睛

】本题考查比较幂的大小，同底数的幂可利用指数函数的单调性比较，不同底数的幂可借助中间值为1比较大小．6.体内癌细胞初期增加得很缓慢，但到了晚期就急剧增加，画一幅能反映体内癌细胞数量随时间变化的示意图.【答案】见解析【解析】【分析】定义域是[0,)+

．是增函数，开始图象较平缓，后来急剧上升，结合指数函数图可得．【详解】经时间x，癌细胞数量为y，图象如图.【点睛】本题考查增长问题，考查指数函数的应用．习题4.2复习巩固7.求下列函数的定义域：（1）32xy−=；（2

）213xy+=；（3）512xy=；（4）10.7xy=.【答案】（1）R；（2）R；（3）R；（4）{|0}xx.【解析】【分析】根据指数幂成立的条件即可求函数的定义域．【详解】解：（1）函数32xy−=的定义域为R；（2）函数213xy+=的定义域为R；（3

）函数512xy=的定义域为R；（4）要使函数10.7xy=有意义，则0x，则函数10.7xy=的定义域为{|0}xx．【点睛】本题主要考查指数型函数的定义域，属于基础题．8.一种产品原来的年产量是a

件，今后m年内，计划使产量平均每年比上一年增加%p，写出年产量y（单位：件）关于经过的年数x的函数解析式.【答案】()*(1%),xyapxxm=+N【解析】【分析】由题意可知函数模型为指数型，由此可得函数解析式．【详解】解：由题意，今后m年内，年产量随时

间变化的增长率为1%p+，又原来的年产量是a件，∴()*(1%),xyapxxm=+N．【点睛】本题主要考查函数模型的建立，属于基础题．9.比较满足下列条件的m，n的大小：（1）22mn<；（2）mn0.20.2；（3）(01)nmaaa；（4）(1)mnaaa.【答案】（1）mn

；（2）mn；（3）mn；（4）mn.【解析】【分析】根据指数函数的单调性即可比较大小．【详解】解：（1）∵函数2xy=在R上单调递增，且22mn<，∴mn；（2）∵函数0.2xy=在R上单调递减，且mn0.20.2，∴mn；（3）∵函数()01xy

aa=在R上单调递减，且(01)nmaaa，∴mn；（4）∵函数()1xyaa=在R上单调递增，且(1)mnaaa，∴mn．【点睛】本题主要考查根据指数函数的单调性比较大小，属于基础题．10.设函数0()(1)xfxQr=+，且(10)20.23,(11)23.26ff=

=.（1）求函数()fx的增长率r；（2）求(12)f的值.【答案】（1）0.15；（2）26.75.【解析】【分析】（1）由题意得100110(1)20.23(1)23.26QrQr+=+=，由此可求得答案；（2）代入解析式即可

求出(12)f．【详解】解：（1）由已知得100110(1)20.23(1)23.26QrQr+=+=，解得00.155rQ.所以增长率r约为0.15.（2）由（1）知，()5(10.15)xfx=+，∴1212(12)5(10.15)51.1526.75f=+=.【点睛】本

题主要考查指数的运算，属于基础题．综合运用11.求下列函数可能的一个解析式：（1）函数()fx的数据如下表：x012()fx3.504.205.04（2）函数()gx的图象如图：【答案】（1）()0.703.50fx

x=+；（2）1()42xgx=．【解析】【分析】（1）通过描点可以判断函数可以近似看成一次函数，设()fxaxb=+，再代入其中两点即可算出答案；（2）由图象可知函数模型为指数型，设()

xgxka=，代入两点坐标即可求出答案．【详解】解：（1）设()fxaxb=+.把(0,3.50),(1,4.20)代入得，3.504.20bab==+，解得0.703.50ab==，()0.703.50fxx=+为可能的解析式；（2）设()xgxka=，将(1,

2),(1,8)−代入，得128kaka−==，解得124ak==，∴1()42xgx=为一个可能的解析式．【点睛】本题主要考查根据图象建立合适的函数模型，属于开放性的基础题．12.比较下列各题中两个值的大小：（1）0.83，0.73；（2）0.1

0.75−，0.10.75；（3）2.71.01，3.51.01；（4）3.30.99，4.50.99.【答案】（1）0.830.73；（2）0.10.75−0.10.75；（3）2.71.013.51.01；（4）3.30.994

.50.99.【解析】【分析】利用指数函数的单调性即可比较大小.【详解】（1）由3xy=单调递增，0.80.7，所以0.830.73；（2）由0.75xy=单调递减，0.10.1−，所以0.10.75−0.10.75；（3）由1.01xy=单调递增，2.73.5，所以2.

71.013.51.01；（4）由0.99xy=单调递减，3.34.5，所以3.30.994.50.99.13.当死亡生物组织内碳14的含量不足死亡前的千分之一时，用一般的放射性探测器就测不到碳14了.如果死亡生物组织内的碳14经过九个“半衰期”后，那么用一

般的放射性探测器能测到碳14吗？【答案】能【解析】【分析】碳14的含量呈指数型变化，由此可得出结论．【详解】解：由题意，经过九个“半衰期后”，碳14的含量为911125121000=，所以能探测到．【点睛】本题主要考查指数函数的应用，属于基础题．14.按复利计

算利息的一种储蓄，本金为a（单位：元），每期利率为r，本利和为y（单位：元），存期数为x.（1）写出本利和y关于存期数x的函数解析式；（2）如果存入本金1000元，每期利率为2.25%，试计算5期后的本利和.【答案】（1）(1)xyar=+.（2

）1117.68y（元）.【解析】【分析】（1）根据题意，结合复利的含义，分析可得本利和y随x变化的函数关系式；（2）根据（1）的函数表达式，代入数据即可计算5期后的本利和．【详解】解：（1）根据题意可得(1)xyar=+；

（2）由（1）可知，当5x=时，51000(12.25%)y=+510001.022111.5768=，∴5期后的本利和约为1117.68元．【点睛】本题主要考查指数函数的应用，属于基础题．拓广探索15.已知函数()||12xfxab=+

的图象过原点，且无限接近直线2y=但又不与该直线相交.（1）求该函数的解析式，并画出图象；（2）判断该函数的奇偶性和单调性.【答案】（1）||2122xy=−+，图象见解析；（2）()fx为偶函数，()fx在(,0]−上为减函数，在[0,)+上为增函数.【解析】【分析】（1）

由函数图象过原点可得0ab+=，又由图象无限接近直线2y=可得2b=，由此可求出函数的解析式，去掉绝对值再结合指数函数图象特征即可画出函数图象；（2）利用奇偶性的定义即可判断函数的奇偶性，去掉绝对值得()122,02122,02xxxfxx−−+=

−+，根据单调性的性质即可求得函数的单调性．【详解】解：（1）由题意知，0,2abb+==，2a=−，()||1222xfx=−+，∴()122,02122,02xxxfxx−−+=−+，图象如图：（2）

∵||1()222xfx=−+，∴1()222xfx−−=−+122()2xfx=−+=，()fx为偶函数，又()122,02122,02xxxfxx−−+

=−+，∴()fx在(,0]−上为减函数，在[0,)+上为增函数．【点睛】本题主要考查指数函数图象的应用，属于基础题．16.已知f(x)=ax，g(x)=1xa(a>

0，且a≠1).（1）讨论函数f(x)和g(x)的单调性；（2）如果f(x)<g(x)，那么x的取值范围是多少？【答案】（1）答案见解析；（2）当a>1时，x的取值范围是(,0)−；当0<a<1时，x的取值范围是(0,

)+.【解析】【分析】（1）由题意按照a>1、0<a<1分类，结合指数函数的性质即可得解；（2）由题意转化条件得0()()1xfxgxaa=，按照a>1、0<a<1分类，结合指数函数的性质即可得解.

【详解】（1）当a>1时，f(x)=ax是R上的增函数，由于0<1a<1，所以g(x)=1xa是R上的减函数；当0<a<1时，f(x)=ax是R上的减函数，由于1a>1，所以g(x)=1x

a是R上的增函数；（2）()201()()11xxxxfxgxaaaaa=，当a>1时，x<0；当0<a<1时，x>0.∴当a>1时，x的取值范围是(,0)−；当

0<a<1时，x的取值范围是(0,)+.