【文档说明】2023届数学一轮复习函数与导数：12.切割线放缩【高考】.docx，共(2)页，212.959 KB，由小赞的店铺上传

转载请保留链接：https://www.doc5u.com/view-b65673dcb816a57ea67874e3747a7b2e.html

以下为本文档部分文字说明：

112.切割线放缩.双变量放缩主要指切割线放缩，此时题干所给函数具有明显的凸凹性，我们可以借助切线不等式的原理将某些变量进行合理的放缩得到结果.1.已知函数()21xxfxe−=(e为自然对数的底数)

.(1)求函数()fx的零点0x，以及曲线()yfx=在0xx=处的切线方程；(2)设方程()fxm=(0m)有两个实数根1x，2x，求证：121212xxme−−+.解：（1）曲线()yfx=在1x=−

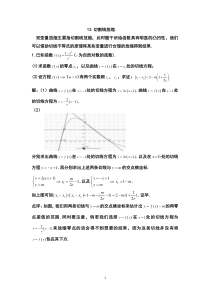
处的切线方程为()21yex=+.曲线()yfx=在1x=处的切线方程为()21yxe=−−.（2）分别求出曲线()yfx=在1x=−处的切线方程为()21yex=+.以及在0=x处的切线方程1+−=xy.再分别求出上述

两条切线与my=的交点横坐标.12)1(2'1−==+=emxmyxey,以及mxmyxy−==+−=11'2.如上图可知)211(2)12(1||||'2'121ememmxxxx+−=−−−=−−.证毕.点评：如图，我们用两条切线与my=的交点横

坐标来估计出mxfy−=)(的两零点差值的范围.同时要注意，倘若我们选择()yfx=在1x=处的切线方程为()21yxe=−−来放缩零点的话会得不到想要的结果，因为这条切线并没有将()yfx=包在其下方.

2