【文档说明】专题02 方法篇：求数列的通项公式（重难点突破）解析版 -【课后辅导专用】2022年春季高二数学下学期精品讲义（人教A版2019）.docx，共(16)页，808.908 KB，由管理员店铺上传

转载请保留链接：https://www.doc5u.com/view-b0a72938e3c61e0fd1c199735be73b8c.html

以下为本文档部分文字说明：

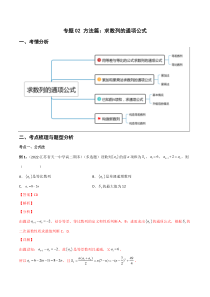
专题02方法篇：求数列的通项公式一、考情分析二、考点梳理与题型分析考点一、公式法例1、（2022·江苏省天一中学高二期末）（多选题）设数列na的前n项和为nS，16a=，12nnaa++=，则（）A．na是等比数列B．na是单调递增数列C

．82nan=-D．nS的最大值为12【答案】CD【解析】【分析】由题设12nnaa+−=−，结合等差、等比数列的定义和性质判断A、B；进而求出na的通项公式，根据nS的二次函数性质求最值判断C、D.【详解】由题设知：12nnaa+−=−，故n

a是等差数列且递减，又16a=，所以62(1)82nann=−−=−，且21()749(7)()224nnnaaSnnn+==−=−−+，当3n=或4n=，nS的最大值为12.综上，A、B错误，C、D正确.故选：C

D【变式训练1-1】、（2022·安徽·六安一中高二期末）设数列na的前n项和为nS，若157,15aS=−=−，且nSn是等差数列．则12310aaaa++++的值为__________．【答案】52【解析】【分析】根据给定条件求出nS，再

求出数列na的通项即可计算作答.【详解】依题意，因nSn是等差数列，则其公差513(7)511514SSd−−−−===−，于是得1(1)7(1)81nSSndnnn=+−=−+−=−，28nSnn=−，当2n时，2218[(1)8(1)]29nnnaSSn

nnnn−=−=−−−−−=−，而17a=−满足上式，因此，29nan=−，所以12310(7531)(1357911)52aaaa++++=−−−−−++++++=.故答案为：52例2、（福建省漳州市2021-2022学年高二上学期期末质量检测

数学试题）已知等差数列na的前n项和为nS，33a=，且410S=.(1)求数列na的通项公式；(2)证明：数列22nnaa+的前n项和32nT.【答案】(1)nan=(2)证明见解析.【

解析】【分析】（1）设等差数列na的公差为d，根据题意可得出关于1a、d的方程组，解出这两个量的值，可得出数列na的通项公式；（2）求得22112nnaann+=−+，利用裂项法可求得nT，即可证得原不等式成立.(1)解：设等差数列

na的公差为d，则3141234610aadSad=+==+=，解得11ad==，因此，()11naandn=+−=.(2)证明：()2221122nnaannnn+==−++，因此，11111

1111111324352212nTnnnn=−+−+−++−=+−−+++()()32332122nnn+=−++.故原不等式得证.【变式训练1-2】、（福建省三明市普通高中2021-2022学年高二上学期期末质量检测数学试题）已知等差数

列na}的公差为整数，nS为其前n项和，37a=，123105aaa=．(1)求{na}的通项公式：(2)设1nnbS=，数列nb的前n项和为nT，求8T．【答案】(1)21nan=+(2)2945【解析】【分析】（1）根据题意利用等差数列的性质列出方程，即可解得答

案；（2）根据（1）的结果，求出1nnbS=的表达式，利用裂项求和的方法求得答案.(1)设等差数列{na}的公差为d，则()()7277105dd−−=,整理可得：2221340dd−+=，∵d是整

数，解得2d=，从而1323aad=−=，所以数列{na}的通项公式为：()31221nann=+−=+;(2)由（1）知，()213222nnnSnnn−=+=+，21111222nbnnnn==

−++所以81111111111111129213243581021291045T=−+−+−++−=+−−=考点二、累加法与累乘法例3、（2022·安徽黄山·一模（理））已知数列na满足12a=，()1221nnnaan++=+，则20211232

020aaaaa=++++___________.【答案】10111010【解析】【分析】利用累乘法可求得数列na的通项公式，利用错位相减法可求得122020+++aaa，即可求得所求代数式的值.【详解】因为数列na满足12a=，()1221nnnaan++=+，则(

)1221nnnaan++=+，所以，当2n时，()()132112121232421223nnnnnaaaaanaaan−−+===+，12a=也满足()112nnan−=+，所以，对任意的N

n，()112nnan−=+.令122020Saaa=+++，则012201922324220212S=++++，可得1220192020222322020220212S=++++，上述两个等式作差得()20191

220192020202020202122222202122202122020212S−−=++++−=+−=−−，所以，202012202020202aaaS+++==，因此，20202021202012320202022210

11=202021010aaaaa=++++.故答案为：10111010.【变式训练3-1】、（2022·上海市控江中学高二期末）己知数列na满足111,2(,1)nnaaannn+==+N，则其通项公式na=________．【答案】2n

n1−+【解析】【分析】利用累加法即可求出数列na的通项公式.【详解】因为12nnaan+=+，所以12nnaan+−=，所以212aa−=，324aa−=，436aa−=，…，()121nnaan−−=−，把以上1n−个式子相加，得()()()()()213243124621nna

aaaaaaan−++++++++−−−=−−……，即()()122212nnana+−−−=，所以2211nnnaann=−+=−+.故答案为：2nn1−+.例4、（2021·河北·沧州市一中高三阶段练习）已知数列na中，112a=，且满足1(

1)nnnana+=+.(1)求数列na的通项公式；(2)设112nnnba+=−，若对任意的*Nn，数列nb是单调递减数列，求实数的取值范围.【答案】(1)2nna=(2)1,3+【解析】【分析】（1）

利用累乘法求得na.（2）由10nnbb+-<分离常数，结合函数的性质求得的取值范围.(1)依题意0na，故11nnanan++=，从而11nnanan−=−，2n，故3212112nnnaaaan

aaaa−==，2nna=，当1n=时，上式也符合，所以2nna=.(2)由（1）知，112221nnnnban+=−=−+，若对任意的*Nn，数列nb是单调递减数列，则1422021nnnbbnn+−=−−++

对任意的*Nn恒成立，即4221maxnn−++，又()()4222221123nnnnnnn−==++++++，因为函数()20yxxx=+在区间()0,2上单调递减，在()2,+上单调递增，所以由对勾函数的性质可知，当1n=或2n=时，23nn++取得最小值

6，即4221nn−++取得最大值13，故实数的取值范围为1,3+.【变式训练4-1】、（2022·浙江柯桥·高二期末）已知等差数列na中，16a=，前5项的和为590S=，数列nb满足11b=，()*12

Nnnnbbn+−=．(1)求数列na，nb的通项公式；(2)记nnncab=−，求数列nc的前n项和nT．【答案】(1)()6N*nann=，()*21Nnnbn=−；(2)()()2112342242

34665nnnnnnTnnn+++−+=−−+.【解析】【分析】（1）利用等差数列求和公式可得6d=，进而可得()6N*nann=，再利用累加法可求nb，即得；（2）由题可得()()62142615nnnnnnncabnn−+=−=−−，然后利用分组求和法即

得.(1)设公差为d，由题设可得5456902d+=，解得6d=，所以()6N*nann=；当2n时，2123221111222222nnnnnbbbbbbbb−−−−=−=−=+++−=，∴

122112nnnb−==−−，当1n=时，11b=（满足上述的nb），所以()*21Nnnbn=−．(2)∵()()62142615nnnnnnncabnn−+=−=−−．当4n时，()()21271361222nnnTcccn=+++=++++−++

+()()212761212nnn−++=−−213422nnn+=+−+．当5n时，()()561234222313761nnnTcccn=+++=++++−+++()()()54212463234122nnn−−−

+=+−−1223466nnn+=−−+．综上所述：()()211234224234665nnnnnnTnnn+++−+=−−+．考点三、已知前n项和，求通项公式例5、（2021·四川省通江中学高二阶段练习（理））已知数列{an}的前n项和为Sn，且2Sn＝3a

n﹣3．(1)求数列{an}的通项公式；(2)设3lognnba=，11nnncbb+=，求数列{cn}的前n项和Tn．【答案】(1)3nna=(2)1nnTn=+【解析】【分析】（1）利用11,1,2nnnSnaSSn−==−来求得na.（2）利

用裂项求和法求得nT.(1)依题意233nnSa=−①，当1n=时，111233,3aaa=−=.当2n时，11233nnSa−−=−②，①-②得11233,3nnnnnaaaaa−−=−=，所以na是首项为13a=，公比为3的等比数列，所以

3nna=，当1n=时，上式也符合，所以3nna=.(2)3log3nnbn==，()11111ncnnnn==−++.所以11111111223111nnTnnnn=−+−++−=−=+++L.【变式训练5-1】、（20

22·山西运城·高三期末（理））已知数列na的前n项和nS，满足3322nnSa=−.(1)求数列na的通项公式；(2)若143cosnnnnbnaa+=，求数列nb的前2n项和2nT.【答案】(1)3nna=(2)2221133nnnT+−=【解析】【

分析】由11as=，代入1n=计算可得1a，由1nnnaSS−=−代入得到13nnaa−=，从而证明数列na是等比数列，求出通项公式；（2）由余弦的周期性可知()cos1nn=−，代入na通项公式可得()111133nnnnb+=−+，计算可求出前2n项和

.(1)1113322aSa==−，算得13a=当2n时，1133332222nnnnnaSSaa−−=−=−−−；得到13nnaa−=13(2)nnana−=所以数列na是以3为首项，3为公比的等比

数列，由11nnaaq−=，得到3nna=(2)由143cosnnnnbnaa+=，得到()()114311113333nnnnnnnnb++=−=−+.2223342122211111111111

()3333333333nnnnnT−+=−−+++−−++−−++2221211113333nnnnT++−=−+=.【变式训练5-2】、（2022·全国·高三专题练习）数列na满足()*

121224N2nnnaanan−+++=−，(1)求3a的值；(2)求数列na前n项和nT；(3)令11ba=，()11111223nnnTbannn−=+++++，证明：数列nb的前n项和nS满足22lnnSn

+．【答案】(1)14；(2)1122n−−；(3)证明见解析.【解析】【分析】(1)根据已知条件，分别取n＝1，2，3即可依次算出123,,aaa；(2)用作差法求出na的通项公式，再求其前

n项和；(3)求123,,SSS，猜想nS，用数学归纳法证明nS；用导数证明()ln1(0)1xxxx++，令1xn=，得11ln11nn++，用这个不等式对nS放缩即可得证.(1)依题()()312312312132223323244224aaaaaa−−++=++−+

=−−−=，314a=；(2)依题当2n时，()()121211212122144222nnnnnnnnnnaaanaaana−−−−++=++−++−=−−−=，112nna−=，又1012

412a+=−=也适合此式，112nna−=，数列na是首项为1，公比为12的等比数列，故1111221212nnnT−−==−−；(3)111ba==，1111Sb

T==，1221122Tba=++，()1212121221111112222TSSbTaTaT=+=+++=++=+，()2323232331111111111123232323

TSSbTaTaT=+=+++++=+++=++，猜想：1112nnSTn=+++①下面用数学归纳法证明：(i)当n＝1，2时，已证明①成立；(ii)假设当nk=时，①成立，即1112kkSTk=+++.从而1111111

112121kkkkkkTSSbTakkk+++=+=++++++++++()111121kkTak+=+++++111121kTk+=++++.故①成立.先证不等式()ln1(0)1xxxx++②令()()ln11xgxxx=+−+，则()22

110(0)1(1)(1)xgxxxxx=−=+++.()()00(0)gxgx=，即②成立.在②中令1xn=，得到111ln1111nnnn+=++③当1n=时，12S；当2n

…时，由①及③得：1112nnSTn=+++111ln2ln1ln121nTn++++++−()()111ln2ln3ln2(lnln122nnn−=++−+

+−−−()21lnn+.证明完毕.【点睛】本题是数列的综合性大题，关键是猜想nS，并用数学归纳法证明nS；根据结论构造不等式()ln1(0)1xxxx++，令1xn=，得11ln11nn+

+，然后用这个不等式对nS放缩.考点四、构造新数列例6、（2022·安徽·合肥市第十一中学高二期末）已知数列na满足13a=，()*121Nnnaan+=+.(1)求证：数列1na+是等比数列；(2)求数列n

a的通项公式及前n项的和nS.【答案】(1)证明见解析；(2)121nna+=−，224nnSn+=−−.【解析】【分析】（1）证明出1121nnaa++=+，即可证得结论成立；（2）由（1）的结论并

确定数列1na+的首项和公比，可求得数列na的通项公式，再利用分组求和法可求得nS.(1)证明：因为数列na满足13a=，()*121Nnnaan+=+，则()1121nnaa++=+，且114a+=，则218a+=，3116a+=，L，以此类推可知，对任意的Nn，10na+，

所以，1121nnaa++=+，故数列1na+为等比数列.(2)解：由（1）可知，数列1na+是首项为4，公比为2的等比数列，则111422nnna−++==，所以，121nna+=−，因此，()()()()()23412341212121

212222nnnSn++=−+−+−++−=++++−()222122412nnnn+−=−=−−−.例7、（2022·山西太原·高三期末（文））已知数列na中，12a=，()*121Nnnaann+=−+.(1)求2a、3a、4a，并证明nan−为等比数列；(2)求数列

na的前n项和nS.【答案】(1)24a=，37a=，412a=，证明见解析；(2)nS2222nnn+−=+.【解析】【分析】（1）利用递推公式可求得2a、3a、4a的值，计算得出()()112+

−+=−nnanan，可证得结论成立；（2）求出数列na的通项公式，利用分组求和法可求得nS.(1)证明：由已知可得2124aa==，32217aa=−=，432212aa=−=，由条件可得()()112+−+=

−nnanan，又111a−=，所以nan−是首项为1，公比为2的等比数列.(2)解：由（1）得12nnan−−=，则12nnan−=+，所以，()()()()01212122232nnSn−=++++++++()()()201211122222212321222nnnnn

nnn−+−+−=+++++++++=+=+−.【变式训练6-1】、（2022·江苏镇江·高二期末）已知数列na满足111,21,.nnaaanN+==+(1)证明数列1na+是等比数列，并求数列n

a的通项公式；(2)令(1)nnbna=+，求数列nb的前n项和.nT【答案】(1)证明见解析，21nna=−(2)1(1)22.nnTn+=−+【解析】【分析】（1）根据等比数列的定义证明数列1na+是以2为首项，2为公比的等比数列

，进而求解得答案；（2）根据错位相减法求和即可.(1)解：数列na满足111,21,.nnaaanN+==+112(1)nnaa++=+Q，∴数列1na+是以112a+=为首项，2为公比的等比数列，11

222nnna−+==，即21nna=−；∴21nna=−(2)解：(1)2nnnbnan=+=Q，231222322nnTn=++++，23412122232(1)22nnnTnn+=++++

−+，2311112(21)22222222221nnnnnnnTnnn++++−−=++++−=−=−−−L，1(1)22.nnTn+=−+【变式训练7-1】、（2022·安徽六安·一模（理））设数列na的前n项和为nS，

已知122nnnSa+=−，Nn.(1)设2nnnab=，Nn，证明：数列nb为等差数列；(2)求数列nS的前n项和nT.【答案】(1)证明见解析(2)2(1)24nnTn+=−+【解析】【分析】（1）把条件122nn

nSa+=−转化为数列nb的递推关系，由等差数列定义去证明即可；（2）以错位相减法去求数列nS的前n项和nT.(1)由122nnnSa+=−，得21122nnnSa+++=−，两式相减得：1122nnnaa++=+两边同除以12n+，得11122nnnnaa++=+，即11nnbb

+=+，当1n=时，由1111122aSa+==−，可得14a=，则1122ab==所以数列{}nb是以2为首项、1为公差的等差数列.(2)由数列{}nb是以2为首项、1为公差的等差数列可得，2(1)11nbn

n=+−=+所以()21nnan=+，()1111222122nnnnnnSann++++=−=+−=则2341122232(1)22nnnTnn+=++++−+345122122232(1)22nnnTnn++=

++++−+则()23412222222124nnnnTnn+++−=++++−=−−()2124nnTn+=−+.