【文档说明】第一章：空间向量与立体几何重点题型复习-【题型分类归纳】2022-2023学年高二数学上学期同步讲与练(人教A版2019选择性必修第一册) （解析版）.docx，共(26)页，3.727 MB，由管理员店铺上传

转载请保留链接：https://www.doc5u.com/view-a914c1e997c0deb8e7710f5da24da1b1.html

以下为本文档部分文字说明：

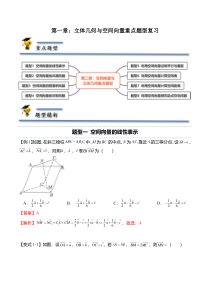
第一章：立体几何与空间向量重点题型复习题型一空间向量的线性表示【例1】如图，在斜三棱柱111ABCABC−中，M为BC的中点，N为11AC靠近1A的三等分点，设ABa=，ACb=，1AAc=，则用a，b，c表示NM为（）A．1126abc+−B．1126abc−++C．1126abc−−D．112

6abc−−+【答案】A【解析】112111()3226NMNCCCCMbcababc→→→→→→→→→→→=++=−+−=+−，故选：A【变式1-1】如图，设OAa=，OBb=，OCc=，若ANNB=，2BMMC=，则MN=（）A．112263abc+−B

．112263abc−−+C．111263abc−−D．111263abc−++【答案】A【解析】由题意得：()()21213232MNMBBNCBBAOBOCOAOB=+=+=−+−=11211226326

3OAOBOCabc+−=+−.故选：A【变式1-2】如图，在平行六面体1111ABCDABCD−中，1AAa=，ABb=，ADc=uuurr，点P在1AC上，且1:2:3APPC=，则AP等于（）A．233555abc++

B．322555abc++C．-223555abc++D．322555abc−−【答案】B【解析】因为点P在A1C上，且A1P：PC=2：3，所以1125APAC=所以111125APAAAPAAAC=+=+()1125AAACAA=+−()112255A

AABADAA=++−1322555AAABAD=++322555abc=++故选：B.【变式1-3】如图，在四面体OABC−中，OAa=，OBb=，OCc=，且2OMMA=，BNNC=，则MN=（）A．221332abc++B．221332abc+−rrr

C．211322abc−++D．121232abc−+【答案】C【解析】连接ON，因为BNNC=，所以1()2ONOBOC=+，因为2OMMA=，所以23OMOA=，所以12211()23322MNONOMOBOCOAabc=−=+−=−++．故选：C．题型二空间向量的共面问题【例2】

（多选）给出下列四个命题，其中是真命题的有（）A．若存在实数x，y，使pxayb=+，则p与a，b共面；B．若p与a，b共面，则存在实数x，y，使pxayb=+；C．若存在实数x，y，使MPxMAyMB=+则点P，M，A，B共面；D．若点P，M，A，B共面，则存在实数x，y，使MPxMA

yMB=+．【答案】AC【解析】由向量共面定理可知A正确；当a，b为零向量可知B错误；由向量共面定理可知,,MPMAMB共面，又因为共始点，所以点P，M，A，B共面，故C正确；当M，A，B三点共线，点P与M，A，B不共线时可知D错误.故选：AC【变式2-1】已知O为空间任意一点，A、B、

C、P满足任意三点不共线，但四点共面，且BPmOAOBOC=++，则m的值为（）A．1−B．2C．2−D．3−【答案】C【解析】2OPOBBPmOAOBOC=+=++，∵O为空间任意一点，A、B、C、P满足任意三点不共线，但四点共面，∴211m+

+=，∴2m=−.故选：C【变式2-2】已知空间A、B、C、D四点共面，且其中任意三点均不共线，设P为空间中任意一点，若54BDPAPBPC=−+，则=（）A．2B．2−C．1D．1−【答案】D【解析】54BDPAPBPC=−+54PDPBPAPBPC−=−+53PDPA

PBPC=−+由A、B、C、D四点共面，且其中任意三点均不共线可得531−+=，解之得1=−，故选：D【变式2-3】(1,1,3),(1,4,2),(1,5,)=−=−−=abcx，若,,abc三向量共面，则实数x=（）A．3B．2C．15D．5【答案】D【解析】∵(1,1,3),(

1,4,2)=−=−−ab，∴a与b不共线，又∵abc、、三向量共面，则存在实数m，n使cmanb=+即14532mnmnmnx−=−+=−=，解得2,3,5===nmx．故选：D．【变式2-4

】如图所示，在长方体1111ABCDABCD−中，M为1DD的中点，NAC，且:2ANNC=，求证：1ABNM，，，四点共面．【答案】证明见解析【解析】设1AAaABbADc===，，，则1ABba=−，M为1

DD的中点，112AMca=−，又:2ANNC=，()2233ANACbc==+，()()1111222122333233ANANAAbcabacaABAM=−=+−=−+−=+，111ANABAM，，为共面向量，又三向量有相同的起点1A，1ABNM

，，，四点共面．题型三空间向量的数量积问题【例3】如图，三棱锥PABC−中，PAB△和ABC都是等边三角形，2AB=，1PC=，D为棱AB上一点，则PDPC的值为（）A．12B．1C．32D．13【答案】A【解析】取AB的中点E，连接,PECE，PAB

△和ABC都是等边三角形，,PEABCEAB⊥⊥，PECEE=，PE平面PEC，CE平面PEC，AB⊥平面PEC，PC面PEC，ABPC⊥，在APC△中，2APAC==，1PC=，由余弦

定理2224141cos244APPCACAPCAPPC+−+−===，()112142PDPCPAADPCPAPCADPCPAPC=+=+===.故选：A.【变式3-1】四边形ABCD为矩形，SA⊥平面ABCD，连接AC，BD，SB，SC，SD，下列各组运算中，不一定为零的是

（）A．SCBDB．DASBC．SDABD．SACD【答案】A【解析】根据题意，依次分析选项：对于A：若SC与BD垂直，又SA与BD垂直，则平面SAC与BD垂直，则AC与BD垂直，与AC与BD不一定垂直矛盾，所

以SC与BD不一定垂直，即向量SC、BD不一定垂直，则向量SC、BD的数量积不一定为0；对于B：根据题意，有SA⊥平面ABCD，则SAAD⊥，又由ADAB⊥，则有AD⊥平面SAB，进而有ADSB⊥，即向量DA、SBuur一定垂直，则向量DA、SBuur的数量积一定为0；

对于C：根据题意，有SA⊥平面ABCD，则SAAB⊥，又由ADAB⊥，则有AB⊥平面SAD，进而有ABSD⊥，即向量SD、AB一定垂直，则向量SD、AB的数量积一定为0；对于D：根据题意，有SA⊥平面ABCD，

则SACD⊥，即向量SA、CD一定垂直，则向量SA、CD的数量积一定为0.故选：A．【变式3-2】已知a、b都是空间向量，且2,3ab=，则2,3ab−=（）A．3B．6C．23D．56【答案】A【解析】2,3,ab=cos,3cos2abababab

==12ab=−，()23cos2,323ababab−−=−66abab−=12=，2,30,ab−，32,3ab−=，故选：A【变式3-3】四棱柱1111ABCDABCD−的底面ABCD是边长为1的菱形，侧棱长为2，且1160CCBCCDBCD===

，则线段1AC的长度是（）A．6B．342C．3D．11【答案】D【解析】因为111CACACCCDCBCC=+=++，且1160CCBCCDBCD===所以()()2211CACDCBCC=++2221112cos602cos602cos6011111422

22211222CDCBCCCDCBCDCCCBCC=+++++=+++++=所以111CA=，即线段1AC的长度是11.故选：D.【变式3-4】如图，在大小为60°的二面角AEFD--中，四边形ABFE，CDEF都是边长为1的正方

形，则B，D两点间的距离是______．【答案】2【解析】由题意可知BFEF⊥，CFEF⊥，则∠BFC为二面角AEFD--的平面角，故60BFC=．又EDCF∥，故异面直线BF，ED所成角也为60．∵BDBFFEED

=++，∴2222||||||222BDBFFEEDBFFEFEEDBFED=+++++222||||||2||||cos12011112BFFEEDBFED=+++=++−=，∴||2BD=．故答案为：2题型四空间向量的对称问题【例4】求点(2,1,2

)−A关于x轴的对称点的坐标为（）A．(2,1,2)−B．(2,1,2)−−C．(2,1,2)−−D．(2,1,2)−【答案】D【解析】A点关于x轴对称点，横坐标不变，纵坐标与竖坐标为原坐标的相反数，故点的坐标为(2,1,2)−，故选：D【变式4-1】在空间直

角坐标系中，点()5,4,3Q−−−关于平面xOz对称的点的坐标是（）A．()5,4,3−B．()5,4,3−−C．()5,4,3−D．()5,4,3−−【答案】D【解析】点()5,4,3Q−−−关于平面xoz对称的点的横、竖坐标不变，纵坐标为相反

数，因此对称点的坐标是()5,4,3−−．故选：D．【变式4-2】在空间直角坐标系Oxyz−中，点()1,2,3A关于平面xOy的对称点A的坐标是（）A．()1,2,3−B．()1,2,3−C．()1,2,3−D．()1,2,3−−【答案】C【解析】在

空间直角坐标系Oxyz−中，点()1,2,3A关于平面xOy的对称点A的坐标是()1,2,3−.故选：C.【变式4-3】点()2,3,1Av−−+关于x轴的对称点为()',7,6A−，则（）A．215v

=−=−=−，，B．245v==−=−，，C．2108v===，，D．2107v===，，【答案】D【解析】因为点()2,3,1Av−−+关于x轴的对称点为()',7,6A−,所以由对称性知23716v=−=−

−+=，解得2107v===，故选：D题型五利用空间向量证明平行与垂直【例5】已知四棱锥PABCD−中，底面ABCD为正方形，CD⊥平面PAD，PDFD⊥，2PDAD==，E、F分别为AP、AB的中点.求证：DFEC⊥；【答案】证明见解析.【解析】连接FC，∵CD⊥面PAD

，PD面PAD，∴CDPD⊥又PDFD⊥，CDFD、面CFD，CDFDD=，∴PD⊥平面CFD，即PD⊥平面ABCD，∴PDAD⊥∴以D为坐标原点，以DP、DA、DC方向分别为x，y，z轴正向建立空间直角坐标系，则()0,0,0D，()1,1,0E，()0,2,1F，()0,0,2

C∴()0,2,1DF=，()1,1,2EC=−−，∴0DFEC=，∴DFEC⊥.【变式5-1】如图，在正方体1111ABCDABCD−中，M，N分别为1AD，1CD的中点．求证：MN⊥平面1DBD；【答案】证明见解析【解析】如图示：以D为原点，DA、DC、DD1分别为x、y、z轴建

立空间直角坐标系．不妨设正方体的边长为2，则()0,0,0D，()2,0,0A，()2,2,0B，()0,2,0C，()10,0,2D，()12,0,2A，()12,2,2B，()10,2,2C，()1,0,1M

，()0,1,1N．所以()1,1,0MN=−，()10,0,2DD=，()2,2,0DB=，因为()()11,1,00,0,20000MNDD=−=++=，所以1MNDD⊥，则1MNDD⊥同理：2200MN

DB=−++=,即MNBD⊥，故MNBD⊥，又1BDDDD=，BD平面1DBD，1DD平面1DBD，所以MN⊥平面1DBD．【变式5-2】如图，在四棱锥PABCD−中，底面ABCD是直角梯形，//ABCD，1AB=，3AD=，2CD=，2ADC=，平面PBC

⊥平面ABCD，且PBPC=，E为BC的中点，证明：平面PAE⊥平面PBD.【答案】证明见解析；【解析】如图，以D为坐标原点，以DA，DC的方向分别为x，y轴的正方向，建立空间直角坐标系Dxyz−，则()3,0,0A，()3,1,0B，()0,2,0C，

33,,022E.因为PBPC=，E为BC的中点，所以PEBC⊥.因为平面PBC⊥平面ABCD且交于BC，所以PE⊥平面ABCD，令33,,22Pa.则()3,1,0DB=，

33,,022AE−=，33,,22aAP−=，所以0DBAE=，0DBAP=，所以DBAE⊥，DBAP⊥，因为AEAPA=I，AE，AP平面PAE，所以DB⊥平面PAE，因为DB平面PBD，所以平面PBD⊥平面PAE.【变式5-3】

在如图所示的五面体ABCDFE中，面ABCD是边长为2的正方形，AE⊥面ABCD，//DFAE，且112DFAE==，N为BE的中点，M为CD中点.求证：//FN平面ABCD.【答案】证明见解析【解析】如图建立空间直角坐标系，则()0,0,0A，()2,0,0B，()0,2,0D，()0

,0,2E，()1,0,1N，()1,2,0M，()0,2,1F，所以()1,2,0NF=−，又平面ABCD的法向量可以为()0,0,1n=，所以0NFn=，即NFn⊥，又NF平面ABCD，所以//

NF平面ABCD.题型六利用空间向量计算空间角【例6】在正方体1111ABCDABCD−中，直线1BC与AC所成角的余弦值为______．【答案】12【解析】空间一组基底为1,,ABADAA，设正方体的棱长为1，则12BC=，2AC=

．()211111()()()BCACBCCCABBCADAAABADADABADAAABAAAD=++=++=+++201001=+++=．因为11111cos,222BCACBCACBCAC===，所以直线1BC与AC所成角的余弦值为12．故答案为：12【变式6

-1】如图，在四棱柱1111ABCDABCD−中，1AA⊥平面ABCD，底面ABCD满足//ADBC，且12,22ABADAABDDC=====.（1）求证://BD平面11BCD;（2）求直线AB与平面11BCD所成角的正弦值.【答案】

（1）证明见解析；（2）66【解析】（1）在四棱柱1111ABCDABCD−中，11//BBDD，故四边形11BBDD是平行四边形，所以11//BDBD，因为BD平面11BCD，11BD平面11BCD，所以//BD平面11BCD（2）因为1AA⊥平面ABCD，,AB

AD平面ABCD，所以11,AAABAAAD⊥⊥，因为2,22ABADBD===，所以222ABADBD+=，所以ABAD⊥，故1,,ABADAA两两垂直，以A为坐标原点，分别以1,,ABADAA为x轴，

y轴,z轴，建立空间直角坐标系，则11(0,0,0),(2,0,0),(2,4,0),(2,0,2),(0,2,2)ABCBD所以111(2,0,0),(0,4,2),(2,2,0)ABBCBD==−=−设平面11BCD的法向量为

(,,)nxyz=11100nBCnBD==即420220yzxy−=−+=令1x=，则1,2yz==，(1,1,2)n=设直线AB与平面11BCD所成角为，26sin|cos,|6||||26ABnABnABn====.所以直线AB与

平面11BCD所成角的正弦值是66.【变式6-2】如图所示，在四棱锥P-ABCD中，ABCD∥，且90BAPCDP==，若PAPDABDC===，60APD=，则二面角A-PB-C的余弦值为______．【答案】33−【解析】在平面PAD内作PFAD⊥，垂足为F，因为90BAPC

DP==，得AB⊥AP，CD⊥PD，由于AB//CD，故AB⊥PD，从而AB⊥平面PAD，故ABPF⊥，可得PF⊥平面ABCD.以F为坐标原点，FA的方向为x轴正方向，AB为单位长，建立如图所示的空间直角坐标系Fxyz−.所以2,0,02A，20,0,2P，

2,1,02B，2,1,02C−.所以22,1,22PC=−−，()2,0,0CB=，22,0,22PA=−，()0,1,0AB=.设(),,nxyz=是平面PCB的法向量，则

0,0,nPCnCB==即220,2220,xyzx−+−==可取()0,1,2n=−−.设(),,mxyz=是平面PAB的法向量，则0,0,mPAmAB==即220,220.

xzy−==可取()1,0,1m=.则3cos,3nmnmnm==−，由图可知二面角APBC−−的平面角为钝角，所以二面角APBC−−的余弦值为33−.故答案为：33−.【变式6-3】如图，已知AB为圆锥SO底面的

直径，点C在圆锥底面的圆周上，2BSAB==，6BAC=，BE平分SBA，D是SC上一点，且平面DBE⊥平面SAB．（1）求证：SABD⊥；（2）求平面EBD与平面BDC所成角的余弦值．【答案】（1）证明见解析；（2）155【解析】（1）因为2SASBAB===，且BE平分SBA，

所以BESA⊥，又因为平面DBE⊥平面SAB，且平面DBE平面SABBE=，SA平面SAB，所以SA⊥平面BDE，又因为BD平面BDE，所以SABD⊥；（2）取AB的中点M，连接OM，OS，则OM，OS，OA两两垂直，所以以O为坐标原点，以OM为x轴，以OA为y轴，以OS为z轴

。建立如图空间直角坐标系，则(0,0,0)O，(0,1,0)A，(0,1,0)B−，31,,022C−，(0,0,3)S，由（1）知SA⊥平面BDE，所以(0,1,3)AS=−是平面BDE的一个法向量，设平面BDC的

法向量为(,,)mxyz=，因为(0,1,3)BS=，31,,322CS=−则30313022mBSyzmCSxyz=+==−++=，取3z=，则(3,3,3)m=−，因此222222615co

s,50(1)(3)(3)(3)(3)mASmASmAS===+−++−+，所以平面EBD与平面BDC所成角的余弦值为155．题型七利用空间向量计算空间距离【例7】长方体1111ABCDABCD−

中，12ABAA==，1AD=，E为1CC的中点，则异面直线1BC与AE之间的距离是（）A．13B．2121C．23D．22121【答案】D【解析】建立如图所示的空间直角坐标系，则(1,0,0)A，(

1,2,0)B，(0,2,0)C，1(0,2,2)C，(0,2,1)E，(1,2,1)AE=−，1(1,0,2)BC=−，设1BC与AE的公垂线的一个方向向量为(,,)nxyz=，则12020nAExyznBCxz=−++==−+=，取1z=，得2x=，12y=

，即1(2,,1)2n=，又(0,2,0)AB=，所以异面直线1BC与AE之间的距离为2221222122112()12ABndn===++．故选：D．【变式7-1】如图，在长方体1111ABCDABCD−中，12A

DAA==，3AB=，若E为AB的中点，则点1B到平面1DEC的距离为______．【答案】186161【解析】以D为坐标原点，DA、DC、1DD所在直线分别为x轴、y轴、z轴，建立如图所示的空间直角坐标系，连

接1CB，由题意得()0,3,0C，32,,02E，()10,0,2D，()12,3,2B，∴32,,02CE=−，()10,3,2CD=−，()12,0,2CB=．设平面1DEC的法向量为(),

,nxyz=r，则100CEnCDn==，即3202320xyyz−=−+=，令6z=，得()3,4,6n=，∴点1B到平面1DEC的距离1186161nCBdn==．故答案为：186161【变式7-2】如图，在四棱锥PABCD−中，ACBDO=，底面AB

CD为菱形，边长为2，60ABC=，PO⊥平面ABCD，异面直线BP与CD所成的角为60°，若E为线段OC的中点，则点E到直线BP的距离为______．【答案】32【解析】连接BE．以O为坐标原点，向量OB，OC，OP的方向分别为x，y，z轴的正方向，建立空间

直角坐标系，ABCD，PBA为异面直线PB与CD所成角，即60PBA=.在菱形ABCD中，2AB=，60ABC=，1OA=，3OB=．设POa=，则21PAa=+，23BPa=+．在PBA△中，由2222cosPABABPBABPPBA=

+−22211432232aaa+=++−+，可得6a=，()3,0,0B，()0,0,6P，10,,02E，13,,02BE=−，()3,0,6BP=−，点E到直线BP的距离为2232BEBPdBEBP骣

÷ç×÷ç÷ç=-=÷ç÷ç÷ç÷ç桫uuruuruuruur.故答案为：32.【变式7-3】空间直角坐标系中()0,0,0A、()1,1,1B、()1,0,0C）、()1,2,1D−，其中A，B，C，D，已知平面//平面，则平面与平面间的距离为（

）A．2626B．1313C．33D．55【答案】A【解析】由已知得()111AB=，，，()221CD=−，，，()100AC=，，，设向量(),nxyz=，与向量AB、CD都垂直，则00nABnCD=

=，即++02+2+0xyzxyz=−=，取1x=，()13,4n=−，，又平面//平面，则平面与平面间的距离为()()22211+30+402626143+ACndn−=

==−+，故选：A.题型八利用空间向量探究动点存在问题【例8】如图，在四棱锥SABCD−中，SA⊥底面ABCD，底面ABCD是梯形，ADBC∥，且ABSD⊥，1SAABBC===，2AD=．（1）求二面角BSCD−−的大小；（2）已知E为CD中点，问：棱SD上是否存在一点Q，使得BQ与AE垂直

？若存在，请求出SQ的长；若不存在，请说明理由．【答案】（1）56；（2）存在，56SQ=【解析】（1）因为SA⊥面ABCD，,ABAD面ABCD，所以SAAB⊥，SAAD⊥．ABSD⊥,SDSAA=,,SDSA平面SAD，所以AB⊥平面SAD，而AD平面SAD，所以ABAD⊥分别以AB

，AD，AS为x，y，z轴建立如图所示的空间直角坐标系，则(1,0,0)B，(1,1,0)C，(0,2,0)D，(0,0,1)S，13,,022E．设平面SBC的一个法向量()1111,,xnyz

=，平面SCD的一个法向量()2222,,nxyz=．因为(1,0,1)SB=−，(0,1,0)BC=，10=nSB，10nBC=．所以11100xzy−==，取11x=，得11z=．所以1(1,0,1)n=．因为(1,1,1)SC=−，(0,2,1)=−

SD，20=nSC，20=nSD，所以22222020xyzyz+−=−=，取21y=得21y=，22z=，所以2(1,1,2)n=．因121212cos,nnnnnn=22222211011232101112++==+++

+，设二面角BSCD−−的大小为，为钝角，则123coscos,2nn=−=−，而[0,]，所以56=．（2）假设线段SD上存在一点Q，使得BQ与AE垂直，设=SQSD，[0,1]，可得(0,2,1)Q

−，BQ(1,2,1)=−−，13,,022AE=，因为BQAE⊥，所以BQAE1302=−+=，解得16=．1566SQSD==．【变式8-1】如图，在矩形ABCD中，1AB=，2BC=，E为边AD上的动点，将

DCE沿CE折起，记折起后D的位置为P，且P在平面ABCD上的射影O恰好落在折线CE上．（1）设DCE=，当为何值时，PBC的面积最小？（2）当PBC的面积最小时，在线段BC上是否存在一点F，使平面PAF⊥平面POF，若存在求出BF的长，若不存在，请说明理由．【答案】（1）π4=；（2）

且1BF=或12BF=【解析】（1）因为2,1BCPC==,所以1sinsin2BCPSBCPCPCBPCB==，由于PO⊥平面BCEA，PCE=，故在RtPOC中，sin,cosPOOC==，在BOC中，π2BC

O=−由余弦定理可得2222π2cos4cos22cossin2OBBCOCBCOC=+−−=+−，在RtPOB中，22222sin4cos22cossin52sin2PBOPOB=+=++−

=−在PBC中，()2221452sin2sin2cos242PCBCPBPCBPCBC+−−+−===因为π0,2，所以()20,π，当sin21=时，即ππ224==，cosPCB最大，此时sinPC

B，而sinBCPSPCB=也为最小值，故π4=（2）以B为坐标原点，以,BCBA为,xy轴的正方向，过B向上作平面ABCE的垂线为z轴正方向，如图，建立空间直角坐标系()31(0,0,0),0,1,0,(2,0,0),(

1,1,0),(,,0),22BACEO当π4=时，此时E是AD中点，故21,2PCPEPO===，故312(,,)222P设()(,0,0),02Faa，则3122312(,,),0,0,,,,)222222

2FPaOPAP=−==−设平面POF的法向量为(),,mxyz=，所以312002220202axyzmFPmOPz−++====，取1x=，则()1,23,0

ma=−同理可得平面PAF的法向量为31,,2ana−=，因为平面PAF⊥平面POF，所以0mnmn⊥=urrurr，即212301aaa+−==或12a=，故存在点F,使得平面PAF⊥平面POF，且1BFa

==或12BF=【变式8-2】如图，在直三棱柱111ABCABC−中，1111ABACF=，为11BC的中点，DE，分别是棱1BCCC，上的点，且ADBC⊥．（1）求证：直线1//AF平面ADE；（2）若ABC是正三角形E，为1CC中点，能否在线段1BB上找一点N，使

得1//AN平面ADE？若存在，确定该点位置；若不存在，说明理由．【答案】（1）证明见解析；（2）在直线1BB上存在一点N，且112BNBB=，使得1//AN平面ADE．【解析】（1）在直三棱柱111ABCABC−中，ABACADBCD=⊥，，

是BC的中点，又F为11BC的中点1//DFAA，而1DFAA=，四边形1DFAA是平行四边形，1//AFAD1AF平面ADEAD，平面ADE，1//AF∴平面ADE．（2）在直线1BB上找一点N，使

得1//AN平面ADE，证明如下：在直三棱柱111ABCABC－中，1//DFAADFADDFDC⊥⊥，又ADBCDADCDF⊥，，两两垂直，以D为原点，DC为x轴，DA为y轴，DF为z轴，建立空间直角坐标系，设11122ABAAt==，，NQ在线段1BB上，设10

1BNBB=，，则(102Nt−,,)，则(0,30),(0,0,0),(1,0,),(1,0,0)ADEtB−,，11(1,0,2),(0,3,2)BtAt−，则(0,3,0)DA=，1(1,0,),(1,3,22)DEtANtt==−−−，设平面ADE的法向量(,,)n

xyz=，则300nDAynDExtz===+=，取1z=，得(,0,1)nt=−，1//AN平面ADE，10220ANnttt=++−=，解得12=，在直线1BB上存在一点N，且112BNB

B=，使得1//AN平面ADE．【变式8-3】如图，在直角梯形ABCD中，ADBC∥，90ADC=，AE⊥平面ABCD，//EFCD，112BCCDAEEFAD=====．（1）求证：BEAF⊥；（2）在直线BC上是否存在点M，使二面角EMDA−−的大小为6？若存在

，求出CM的长；若不存在，请说明理由．【答案】（1）证明见解析；（2）存在，33CM=.【解析】（1）如图，作//FGEA，//AGEF，连接EG交AF于H，连接BH，BG，∵//EFCD且//EFAG，∴//AGCD，即点G在平面ABCD内．在平行四边形CDAG中，90ADC=，∴BGAG

⊥，又由AE⊥平面ABCD知AEBG⊥，∴BG⊥平面AEFG，∴BGAF⊥①在矩形AEFG中，AEEF=，∴AFEG⊥②∴由①②知，AF⊥平面BGE，∴AFBE⊥．（2）如图，以A为原点，AG为x轴，AD为y轴，AE为z轴，建立空间直角坐标系Axyz−，则()0,0,0A，

()1,0,0G，()0,0,1E，()0,2,0D，设()01,,0My，∴()0,2,1ED=−，()01,2,0DMy=−，设平面EMD的法向量为(),,nxyz=，则()02020nEDyznDMxyy=−==+−=，令1y=，得2z=，02xy=−，∴()02,1,2ny=

−，又AE⊥平面AMD，∴()0,0,1AE=uuur为平面AMD的一个法向量，∴()2023cos,cos621214nAEy===−++，解得0323y=，故在BC上存在点M，且332233CM=−=．