【文档说明】第04讲 位似-2021-2022学年九年级数学下册同步精品随堂讲义+练习+检测(人教版)(解析版).docx，共(22)页，726.209 KB，由管理员店铺上传

转载请保留链接：https://www.doc5u.com/view-9f092397d754cbc1e32bdaab361aba7a.html

以下为本文档部分文字说明：

第04讲位似【教学目标】1.了解位似的概念，会画位似图形，掌握位似图形的性质和位似图形的坐标变化规律，了解平移、轴对称、旋转和位似之间的联系与区别2.经历探索位似图形的概念及画法的过程，培养学生的动手操作能力和发现、探索规律的能力3.体验学习数学的乐趣【教学建议】《相似》是

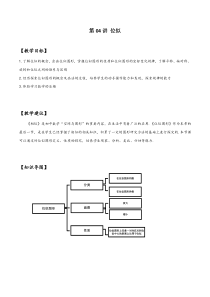
初中数学“空间与图形”的重要内容，在生活中有着广泛的应用.《位似图形》作为本章的最后一节，是在学生已经掌握了相似的相关知识，积累了一定的图形研究方法的基础上进行探究的.本节课可以通过对位似图形定义、性质的探究，培养学生观察、分析、类比、归纳等能力.【知识导图】位似图形分类在位似图形同侧在位似图形异

侧画图放大缩小性质位似图形上任意一对对应点到位似中心的距离之比等于位似【复习预习】性质：(1)相似三角形的对应角相等.(2)相似三角形的对应边成比例.(3)相似三角形的对应高线的比，对应中线的比和对应角平分线的比都等于相似比.(4)相似三角形

的周长比等于相似比.(5)相似三角形的面积比等于相似比的平方.判定：对应角相等，对应边成比例的两个三角形叫做相似三角形.判定定理1：如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似（AA）判定定理2：如果两个三角形的两组对应边成比例，并且对应的夹角相等，那么这两

个三角形相似（SAS）判定定理3：如果两个三角形的三组对应边成比例，那么这两个三角形相似（SSS）判定定理4：两三角形三边对应平行，则两三角形相似.判定定理5：两个直角三角形中，斜边与直角边对应成比例，那么两三角形相似.上节课我们学习了相似图形及相似三角形的概念及性质和判定，今

天我们共同探讨位似图形特性？【知识讲解】1、位似图形两个多边形不仅相似，而且对应顶点的连线相交于一点，对应边互相平行，像这样的两个图像叫做位似图形，这个点叫做位似中心.例如：如图所示：都是位似图形，其中是以为位似中

心的位似图形，四边形ABCD与四边形为位似中心的位似图形.知识拓展：（1）位似是一种具有特殊位置关系.的相似.两个图形是位似图形，必定是相似图形，而两个图形是相似图形，不一定是位似图形；（2）位似中心可以在两图形内部，两图形之

间，两图形的同一侧，也可以在一个图形的一条边上或某一个点上.111CBAABC与是以与五边形，五边形为位似中心的位似图形是以111111111EDCBAABCDEDCBA（3）利用位似，可以将一个图形放大或缩小.（4）平

行于三角形一边的直线与其他两边或两边的延长线相交，所构成的三角形与原三角形位似.2、作位似图形作位似图形的一般步骤：（1）确定位似中心.画位似图形时，位似中心可以在图形的内部，也可以在图形的外部，还可以在图形的边上.（2）找出图形的关键点（多边形通常取顶点）

，连接位似中心与关键点.（3）根据相似比，确定能代表所作的位似图形的关键点；顺此链接所得的关键点，得到新的图形（4）写出作图的结论.知识拓展：（1）作位似图形时，要弄清相似比，即分清是已知图形与新图形的相似比，还是新图形与已知图形的相似比.（2）一般情况下，作已知图形的位似图形的结果

不唯一.新课导读：利用位似，可以将一个图形放大或缩小.3、位似变换在平面直角坐标系中，如果以原点为位似中心，新图形与原图形的相似比为k,那么与原图形上的点（x,y）对应的位似图形上的点坐标为（kx,ky）或（-kx,-ky）.将原图形中各个顶点

的横坐标纵坐标都乘k,则变化后的图形与原图形关于原点成位似图形，并且相似比为>1时，变化后的图形比原图形大；当<1时，变化后的图形比原图形小.知识拓展：（1）以原点为位似中心的位似变换，其对应点的坐标关系可表示为（新图形与原图形的位似比为k）：P(x,

y)(kx，ky)；P(x，y)（-kx，-ky）（2）当k>1时，图形扩大为原来的k倍；当0<k<1时，图形缩小为原来的k倍.（3）在直角坐标系中，把一个图形进行平移、轴对称、旋转和位似变换，对应点的坐标都有各自的变化规律：①平移变换是横坐标或纵坐标加上(或减去)平移的

距离；②轴对称变换，以x轴为对称轴，则对应点的横坐标相等，纵坐标互为相反数；以y轴为对称轴，则对应kk⎯⎯⎯⎯⎯⎯⎯→⎯同侧对应点位于位似中心的1P⎯⎯⎯⎯⎯⎯⎯→⎯异侧对应点位于位似中心的1P点的纵坐标相等，横坐标互为相反数；③在旋转变换中，一个图形

绕着原点旋转，旋转前后两个图形上的对应点的横纵坐标都互为相反数；④位似变换中，当原点为位似中心时，变换前后两个图形上的对应点的横(或纵)坐标之比等于相似比【例题精析】类型一位似图形例1：下列说法中正确的是（）A.位似图形一定是相似图形B

.相似图形一定是位似图形C.两个位似图形一定在位似中心的同侧D.位似图形中每对对应点所在的直线必互相平行【解析】解：A位似图形一定是相似图形，故A选项正确；B相似图形不一定是位似图形，故B选项错误；C两个位似图形可以在位似中心的同侧或异侧，故C选项错误；D位似图形中每对对应

点所在的直线必交于一点，故D选项错误．故选A．【总结与反思】根据位似图形的定义即可进行判断.变式1：下列关于位似图形的表述：①相似图形一定是位似图形，位似图形一定是相似图形；②位似图形一定有位似中心；③如果两个图形是相似图形，且每组对

应点的连线所在的直线都经过同一个点，那么，这两个图形是位似图形；④位似图形上任意两点与位似中心的距离之比等于相似比．其中正确命题的序号是（）A．②③B．①②C．③④D．②③④【答案】A变式2：如图，在正方形网格中，△ABC和△DEF相似，则关于位似中心与相似比叙述正确的是180A

．位似中心是点B，相似比是2：1B．位似中心是点D，相似比是2：1C．位似中心在点G，H之间，相似比为2：1D．位似中心在点G，H之间，相似比为1：2【答案】C类型二作位似图形例2：如图，方格纸中有一条美丽可爱的小金鱼．（1）在同一方格纸中，画出将小金鱼图案绕原点O旋转180°后得到的

图案；（2）在同一方格纸中，并在轴的右侧，将原小金鱼图案原点O为位似中心放大，使它们的位似比为1：2，画出放大后小金鱼的图案．【解析】解：（1）如图所示：（2）如图所示：【总结与反思】（1）直接根据旋转作图的方法作图即可；（2）根据位似作图的方法作图，，确定能代表所作的位

似图形的关键点；顺次连接上述各点，得到放大的图形．变式1：如图，分别按下列要求作出四边形ABCD以O点为位似中心的位似四边形A′B′C′D′.(1)沿AO的方向放大为原图的2倍；(2)沿OA的方向放大为原图的2倍．【解析】（1）如图所示：四边形A′B′C′D′符合题意；（2）如图所

示：四边形A″B″C″D″符合题意.变式2：已知：△ABC三个顶点的坐标分别为A（–2，–2），B（–5，–4），C（–1，–5）．（1）画出△ABC关于x轴对称的△A1B1C1；（2）以点O为位似中心，将△ABC放大为原来的2倍，得到△A2B2C2，请在网格中画

出△A2B2C2，并写出点B2的坐标．变式3：（1）图1中，以O为位似中心，把△ABC放大到原来的2倍；（2）图2中，以O为位似中心，把△ABC缩小为原来的13．类型三位似图形的坐标变化规律例3：如图，在平面直角坐标系中，矩形

OABC的顶点坐标分别为O（0，0），A（2，0），B（2，1），C（0，1），以坐标原点O为位似中心，将矩形OABC放大为原图形的2倍，记所得矩形为OA1B1C1，B为对应点为B1，且B1在OB的延长线上，则B1的坐标为．【解析】解：∵B点坐标为（2

，1），而B为对应点为B1，且B1在OB的延长线上，∴B1的坐标为（2×2，1×2），即B1（4，2）．故答案为（4，2）．【总结与反思】利用以原点为位似中心的位似图形的坐标之间的关系求解．本题考查了位似变换：在平面直角坐标系中，如果

位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或﹣k．变式1：如图，在平面直角坐标系xOy中，点A的坐标为()12ABx−⊥，，轴于点.B以原点O为位似中心，将OAB△放大为原来的2倍，得到11OAB△，且点1A在第二象限，则点1A的坐标为A．()2

4−，B．112−，C．()24−，D．()24，【答案】A【解析】根据位似的性质可得11112ABBOABBO==，()12A−，，21ABBO==，，11142ABBO==，，当点1A在第二象限时，1A的坐标为()24.−，故选A．变式2：如图，正

方形BODC的顶点C的坐标是()33，，以原点O为位似中心，将正方形BODC缩小后得到正方形BOD'C，点C的对应点C′的坐标为()11−−，，那么点D的对应点D′的坐标为A．()10−，B．()01−，C．()10，D．()01，【答案】A【解析

】∵点C的坐标是(3，3)，∴点D的坐标是(3，0)，∵点C′的坐标为(−1，−1)，∴点D′的坐标为(−1，0)，故选A．变式3：如图，在66的正方形方格中，每个小正方形的边长都为1，顶点都在网格线交点处的三角形，ABC△是一个格点三角形．()1在图①中，请判断ABC△与DEF△是否相似，并说

明理由；()2在图②中，以O为位似中心，再画一个格点三角形，使它与ABC△的位似比为2：1；()3在图③中，请画出所有满足条件的格点三角形，它与ABC△相似，且有一条公共边和一个公共角．【课堂练习】1.在下列图形中，不是位似图形的

是（）A．B．C．D．【答案】D．【解析】解：对应顶点的连线相交于一点的两个相似多边形叫位似图形．根据位似图形的概念，A、B、C三个图形中的两个图形都是位似图形；D中的两个图形不符合位似图形的概念，对应顶点不能相交于一点，故不是位似图形．故选：D．2.如图，△ABC经过位似变换得到△DEF，点O

是位似中心且OA=AD，则△ABC与△DEF的面积比是（）A．1:6B．1:5C．1:4D．1:2【答案】C.【解析】∵△ABC经过位似变换得到△DEF，点O是位似中心且OA=AD，∴AC∥DF，∴△OAC∽△OD

F，∴AC：DF=OA：OD=1：2，∴△ABC与△DEF的面积比是1：4．3.在平面直角坐标系中，线段AB两个端点的坐标分别为A（6，8），B（10，2），若以原点O为位似中心，在第一象限内将线段AB

缩短为原来的后得到线段CD，则点A的对应点C的坐标为（）A．（5，1）B．（4，3）C．（3，4）D．（1，5）【答案】C．【解析】∵以原点O为位似中心，在第一象限内将线段AB缩小为原来的后得到线段CD，∴端点C的横坐标和纵坐标都变为A点的横坐标和纵坐标的一半，又∵A（6，8），∴端

点C的坐标为（3，4）．故选：C．4.如图，在边长为1的小正方形组成的网格中，建立平面直角坐标系，△ABC的三个顶点均在格点（网格线的交点）上．以原点O为位似中心，画△A1B1C1，使它与△ABC的相似比为2，则点B的对应点B1的坐标是．【答

案】（4，2）或（﹣4，﹣2）．【解析】如图所示：△A1B1C1和△A′B′C′与△ABC的相似比为2，点B的对应点B1的坐标是：（4，2）或（﹣4，﹣2）．5.如图，△ABC与△A1B1C1为位似图形，点O是它们的位似中心，位似比是1：2，已知△ABC的面积为3

，那么△A1B1C1的面积是．【答案】12．【解析】解：∵△ABC与△A1B1C1为位似图形，∴△ABC∽△A1B1C1，∵位似比是1：2，∴相似比是1：2，∴△ABC与△A1B1C1的面积比为：1：4，∵△ABC的面积为3，

∴△A1B1C1的面积是：3×4=12．故答案为：12．6.如图，在平面直角坐标系中，△ABC的顶点坐标分别为（4，0），（8，2），（6，4）．已知△A1B1C1的两个顶点的坐标为（1，3），（2，5），若△AB

C与△A1B1C1位似，则△A1B1C1的第三个顶点的坐标为．【答案】解：设直线AC的解析式为：y=kx+b，∵△ABC的顶点坐标分别为（4，0），（8，2），（6，4），∴，解得：，∴直线AC的解析式为：y=2x﹣8，同理可得：直

线AB的解析式为：y=x﹣2，直线BC的解析式为：y=﹣x+10，∵△A1B1C1的两个顶点的坐标为（1，3），（2，5），∴过这两点的直线为：y=2x+1，∴过这两点的直线与直线AC平行，①若A的对应点为A1（1

，3），C的对应点为C1（2，5），则B1C1∥BC，B1A1∥BA，设直线B1C1的解析式为y=﹣x+a，直线B1A1的解析式为y=x+b，∴﹣2+a=5，+b=3，解得：a=7，b=，∴直线B1C1的解析式为y=﹣x+7，直线B1A1的解析式为y=x

+，则直线B1C1与直线B1A1的交点为：（3，4）；②若C的对应点为A1（1，3），A的对应点为C1（2，5），则B1A1∥BC，B1C1∥BA，设直线B1C1的解析式为y=x+c，直线B1A1的解析式为y=﹣x+d，∴×2+c=5，﹣1+d=3，解得：c=4

，d=4，∴直线B1C1的解析式为y=x+4，直线B1A1的解析式为y=﹣x+4，则直线B1C1与直线B1A1的交点为：（0，4）．∴△A1B1C1的第三个顶点的坐标为（3，4）或（0，4）．故答案为：（3，

4）或（0，4）．【解析】首先由题意可求得直线AC、AB、BC的解析式与过点（1，3），（2，5）的直线的解析式，即可知过这两点的直线与直线AC平行，则可分别从①若A的对应点为A1（1，3），C的对应点为C1（2，

5）与②若C的对应点为A1（1，3），A的对应点为C1（2，5）去分析求解，即可求得答案．7.如图，在由边长为1个单位长度的小正方形组成的10×10网格中，已知点O，A，B均为网格线的交点．（1）在给定的网格中，以点O为位似中心，将线段AB放大为原来的2倍，得到线段A1B1（点A

，B的对应点分别为A1，B1），画出线段A1B1；（2）将线段A1B1绕点B1逆时针旋转90°得到线段A2B1，画出线段A2B1；（3）以A，A1，B1，A2为顶点的四边形AA1B1A2的面积是个平方单位．【答案】同解析．【解析】解：（1）如图所示，

线段A1B1即为所求；（2）如图所示，线段A2B1即为所求；（3）由图可得，四边形AA1B1A2为正方形，∴四边形AA1B1A2的面积是（）2=（）2=20．8.已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A（0，3）、B（3，4）、C（2，2）（正方形

网格中每个小正方形的边长是一个单位长度）．（1）画出△ABC向下平移4个单位长度得到的△A1B1C1，点C1的坐标是；（2）以点B为位似中心，在网格内画出△A2B2C2，使△A2B2C2与△ABC位似，且位似比为2：1，点C2的坐标是．【

答案】（1）（2，﹣2））；（2）（1，0）．【解析】解：（1）如图所示，画出△ABC向下平移4个单位长度得到的△A1B1C1，点C1的坐标是（2，﹣2）；（2）如图所示，以B为位似中心，画出△A2B2

C2，使△A2B2C2与△ABC位似，且位似比为2：1，点C2的坐标是（1，0），故答案为：（1）（2，﹣2）；（2）（1，0）9.如图，以原点O为位似中心，把△OAB放大后得到△OCD，求△OAB与△OCD的相似比．【答案】．【解析】解：∵点B的坐标是（4

，0），点D的坐标是（6，0），∴OB=4，OD=6，∴==，∵△OAB与△OCD关于点O位似，∴△OAB与△OCD的相似比．10.如图，已知O是坐标原点，B、C两点的坐标分别为（3，﹣1），（2，1）．（1）以O点为位似中心在y轴左侧将△OBC放大到两倍（即新图与原图的相似比为2），画出图形

；（2）如果△OBC内部一点M的坐标为（x，y），写出B、C、M对应点B′，C′，M′坐标．【答案】同解析．【解析】解：（1）如图所示：△B′C′O即为所求；（2）如图所示：∵B、C两点的坐标分别为（3，﹣1），（2，1），新图与原图的相似比为2，∴B′（﹣6，2），C′（﹣4，﹣2），∵△OB

C内部一点M的坐标为（x，y），∴对应点M′（﹣2x，﹣2y）．【课堂小结】1.知识结构及要点小结−−），）或（，的坐标为（对应点位似图形上的点，，那么与原图形上的（为原图形的相似比为位似中心，新图形与坐标

系中，如果以原点位似变换：在平面直角这个点叫做位似中心像的两个图形叫做位似图对应边互相平行像这样交于一点，而且对应顶点的连线相两个多边形不仅相似，位似图形及相关概念位似kykxkykxyxk)2.解题方法及技巧小结（1）位似图形是增加

了条件的相似图形（2）求两个位似图形的相似比，首先要确定好相似的顺序，然后确定相似比（3）画一个图形的位似图形的方法不唯一，在具体的问题中，可以根据画图的需要选择适当的画图方法【课后巩固】1.在如图所示的四个图形为两个圆或相似的正多边形，其

中位似图形的个数为（）A．1个B．2个C．3个D．4个【答案】C．【解析】解：如图，根据位似图形的定义可知第1、2、4个图形是位似图形，而第3个图形对应点的连线不能交于一点，故位似图形有3个．故选：C．2.如图，在平面直角坐标系中，已知点A（2，4），B（4，1），以原点O为位似中心，将△OAB缩

小为原来的，则点A的对应点A的坐标是（）A．（2，）B．（1，2）C．（4，8）或（﹣4，﹣8）D．（1，2）或（﹣1，﹣2）【答案】D．【解析】解：以O为位似中心，把△OAB缩小为原来的，则点A的对应点A′的坐标为（2×，4×）或[2×（﹣），4×（﹣）]，即（1，2

）或（﹣1，﹣2），故选：D．3.已知在平面直角坐标系中，点A（﹣3，﹣1）、B（﹣2，﹣4）、C（﹣6，﹣5），以原点为位似中心将△ABC缩小，位似比为1：2，则点B的对应点的坐标为．【答案】∵点B的坐标为（﹣2，﹣4），以原点为位似中心将△ABC

缩小，位似比为1：2，∴点B的对应点的坐标为（1，2）或（﹣1，﹣2），故答案为：（1，2）或（﹣1，﹣2）．【解析】根据在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或﹣k解答．4.如图，△A

BC与△DEF位似，位似中心为点O，且△ABC的面积等于△DEF面积的，则AB：DE=．【答案】2：3．【解析】解：∵△ABC与△DEF位似，位似中心为点O，∴△ABC∽△DEF，∴△ABC的面积：△DEF面积=（）2=，∴AB：DE=2：3，故答案为：2：3．5.如图，以点O为位

似中心，将五边形ABCDE放大后得到五边形A′B′C′D′E′，已知OA=10cm，OA′=20cm，则五边形ABCDE的周长与五边形A′B′C′D′E′的周长的比值是．【答案】解：∵五边形ABCDE与五边形A′B′C′D′E′位似，OA=10

cm，OA′=20cm，∴五边形ABCDE∽五边形A′B′C′D′E′，且相似比为：OA：OA′=10：20=1：2，∴五边形ABCDE的周长与五边形A′B′C′D′E′的周长的比为：OA：OA′=1：2．故答案为：1

：2．【解析】由五边形ABCDE与五边形A′B′C′D′E′位似，可得五边形ABCDE∽五边形A′B′C′D′E′，又由OA=10cm，OA′=20cm，即可求得其相似比，根据相似多边形的周长的比等于其相似比，即可求得答案．6.在平面直角坐标

系xOy中，点A、B的坐标分别为（2，﹣1）、（3，0），以原点O为位似中心，把线段AB放大，点B的对应点B′的坐标为（6，0），则点A的对应点A′的坐标为．【答案】（4，﹣2）．【解析】解：∵以原点O为位似中心，

B（3，0）的对应点B′的坐标为（6，0），∴相似比为2，∵A（2，﹣1），∴点A′的对应点坐标为：（4，﹣2），故答案为：（4，﹣2）．7.在如图所示的平面直角坐标系中，△OA1B1是边长为2的等边三角形，作△B2A2B1与△OA1B1关于点B1成中心对称，再作△B2

A3B3与△B2A2B1关于点B2成中心对称，如此作下去，则△B2nA2n+1B2n+1（n是正整数）的顶点A2n+1的坐标是．【答案】（4n+1，）．【解析】∵△OA1B1是边长为2的等边三角形，∴A1的坐标为（1，），B1的坐标为（2，0），∵△B2A2B1与△OA1B1关

于点B1成中心对称，∴点A2与点A1关于点B1成中心对称，∵2×2﹣1=3，2×0﹣=﹣，∴点A2的坐标是（3，﹣），∵△B2A3B3与△B2A2B1关于点B2成中心对称，∴点A3与点A2关于点B2成中心对称，∵2×4﹣3=5，2×0﹣（﹣）=，∴点A3的坐标是（5，），∵△B3A4B4与△

B3A3B2关于点B3成中心对称，∴点A4与点A3关于点B3成中心对称，∵2×6﹣5=7，2×0﹣=﹣，∴点A4的坐标是（7，﹣），…，∵1=2×1﹣1，3=2×2﹣1，5=2×3﹣1，7=2×3﹣1，…，∴An的横坐标是2n﹣1，A2n+1的横坐标是2（2n+

1）﹣1=4n+1，∵当n为奇数时，An的纵坐标是，当n为偶数时，An的纵坐标是﹣，∴顶点A2n+1的纵坐标是，∴△B2nA2n+1B2n+1（n是正整数）的顶点A2n+1的坐标是（4n+1，）．故答案

为：（4n+1，）．8.如图，正方形A1A2B1C1，A2A3B2C2，A3A4B3C3，…，AnAn+1BnCn，如图位置依次摆放，已知点C1，C2，C3，…，Cn在直线y=x上，点A1的坐标为（1，0）．（1）写出正方形A1A2B1C1，A2A3B2C2，A3A4B3C3，…，AnAn+1B

nCn的位似中心坐标；（2）正方形A4A5B4C4四个顶点的坐标．【答案】（1）（0，0）；（2）A4（8，0），A5（16，0），B4（16，8），C4（8，8）．【解析】解：（1）如图所示：正方形A1A2

B1C1，A2A3B2C2，A3A4B3C3，…，AnAn+1BnCn的位似中心坐标为：（0，0）；（2）∵点C1，C2，C3，…，Cn在直线y=x上，点A1的坐标为（1，0），∴OA1=A1C1=1，OA2=A2C2=2，则A3O=A3C3=4，∴可得：OA4=A4C4=8，则OA5=16

，故A4（8，0），A5（16，0），B4（16，8），C4（8，8）．9.已知，△ABC在直角坐标平面内，三个顶点的坐标分别是A（0，3）、B（3，4）、C（2，2），正方形网格中，每个小正方形的边长是一个单位长度．（1）画出△ABC向左平移4个单位长度得到的△A1B1C1，点C1的坐

标是；（2）以点B为位似中心，在网格内画出△A2B2C2，使△A2B2C2与△ABC位似，且位似比为2：1，点C2的坐标是；（画出图形）（3）△A2B2C2的面积是平方单位．【答案】（1）（﹣2，2）；（2）（1，0）；（3）10.【解析】解：（1）如图，△A1B1C1即为所求，点C1的坐

标是（﹣2，2），故答案为：（﹣2，2）；（2）如图所示，△A2B2C2即为所求，点C2的坐标是（1，0），故答案为：（1，0）；（3）△A2B2C2的面积×（2+4）×6﹣×2×4﹣×2×4=10，故答案为：10.获得更多资源请扫码加入享学资源网微信公众号www.xiangxue100

.com