【文档说明】专题21 外接球与内接球相关模型（原卷版）-【重难点突破】2021-2022学年高一数学常考题专练（人教A版2019必修第二册）.docx，共(13)页，1.468 MB，由管理员店铺上传

转载请保留链接：https://www.doc5u.com/view-8511a0546b7e11bc04c769efe581e6aa.html

以下为本文档部分文字说明：

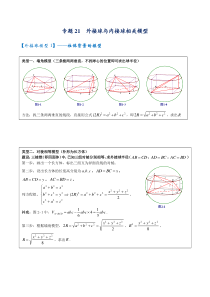
专题21外接球与内接球相关模型【外接球模型1】——柱体背景的模型类型一、墙角模型（三条棱两两垂直，不找球心的位置即可求出球半径）方法：找三条两两垂直的线段，直接用公式2222)2(cbaR++=，即2222cbaR++=，求出Rcab图1-1CPABab

c图1-2PCBAabc图1-3CBPAabc图1-4PCBA类型二、对棱相等模型（补形为长方体）题设：三棱锥（即四面体）中，已知三组对棱分别相等，求外接球半径（CDAB=，BCAD=，BDAC=）第一步：画出一个长方体，标出三组互为异面直线的对棱；第二步：设出长方体的长宽高分别为cba,

,，xBCAD==，yCDAB==，zBDAC==，列方程组，=+=+=+222222222zacycbxba2)2(2222222zyxcbaR++=++=，补充：图2-1中，abcabcabcVBCDA31

461=−=−.第三步：根据墙角模型，22222222zyxcbaR++=++=，82222zyxR++=，8222zyxR++=，求出R.yxabczzyx图2-1DCAB类型三、汉堡模型（直棱柱的外接球、圆柱的外接球）题设：如图3-1，

图3-2，图3-3,直三棱柱内接于球（同时直棱柱也内接于圆柱，棱柱的上下底面可以是任意三角形）第一步：确定球心O的位置，1O是ABC的外心，则⊥1OO平面ABC；第二步：算出小圆1O的半径rAO=1，hAA

OO212111==（hAA=1也是圆柱的高）；第三步：勾股定理：21212OOAOOA+=222)2(rhR+=22)2(hrR+=，解出R例题：（1）直三棱柱的各顶点都在同一球面上，若,，则此球的表面积等于.解：32=BC，4120s

in322==r，2=r，5=R，20=S；（2）一个正六棱柱的底面上正六边形，其侧棱垂直于底面，已知该六棱柱的顶点都在同一个球面上，且该六棱柱的体积为89，底面周长为3，则这个球的体积为解：设正六边形边长为a，正六棱柱的高为h，

底面外接圆的半径为r，则21=a，正六棱柱的底面积为833)21(4362==S，89833===hShV柱，3=h，4)3(14222=+=R也可1)21()23(222=+=R），1=R，球的体积为34=球V；图3-1C1B1AEFA1

O1OO2BC图3-2C1B1AA1O1OO2BC图3-3C1B1AEFA1O1OO2BC111ABCABC−12ABACAA===120BAC=【外接球模型2】——锥体背景的模型类型五、垂面模型

（一条直线垂直于一个平面）类型四、切瓜模型（两个大小圆面互相垂直且交于小圆直径——正弦定理求大圆直径是通法）1．如图4-1，平面⊥PAC平面ABC，且BCAB⊥（即AC为小圆的直径），且P的射影是ABC的外心三棱锥ABCP−的三条侧棱相等三棱ABCP−的底面ABC在圆锥的底上，顶点

P点也是圆锥的顶点.解题步骤：第一步：确定球心O的位置，取ABC的外心1O，则1,,OOP三点共线；第二步：先算出小圆1O的半径rAO=1，再算出棱锥的高hPO=1（也是圆锥的高）；第三步：勾股定理：21212OOAOOA+=222)(rRhR+−=，解出R；事实上，AC

P的外接圆就是大圆，直接用正弦定理也可求解出R.2．如图4-2，平面⊥PAC平面ABC，且BCAB⊥（即AC为小圆的直径），且ACPA⊥，则利用勾股定理求三棱锥的外接球半径：①222)2()2(rPAR+=22)

2(2rPAR+=；②2122OOrR+=212OOrR+=3．如图4-3，平面⊥PAC平面ABC，且BCAB⊥（即AC为小圆的直径）21212OOCOOC+=2122OOrR+=2122OORAC

−=4．题设：如图4-4，平面⊥PAC平面ABC，且BCAB⊥（即AC为小圆的直径）第一步：易知球心O必是PAC的外心，即PAC的外接圆是大圆，先求出小圆的直径rAC2=；第二步：在PAC中，可根据正弦

定理RCcBbAa2sinsinsin===，求出R.图4-1PAO1OCB图4-2AO1OCBP图4-3OO1ACBP图4-4ACBP1．题设：如图5，⊥PA平面ABC，求外接球半径.解题步骤：第一步：将A

BC画在小圆面上，A为小圆直径的一个端点，作小圆的直径AD，连接PD，则PD必过球心O；第二步：1O为ABC的外心，所以⊥1OO平面ABC，算出小圆1O的半径rDO=1（三角形的外接圆直径算法：利用正弦定理，得rCcB

bAa2sinsinsin===），PAOO211=；第三步：利用勾股定理求三棱锥的外接球半径：①222)2()2(rPAR+=22)2(2rPAR+=；②2122OOrR+=212OOrR+=.例题：三棱锥P－ABC中，

平面PAC⊥平面ABC，AB⊥AC，PA＝PC＝AC＝2，4AB=，棱锥P－ABC的外接球的表面积为()A．23B．234C．64D.643【答案】D【解析】显然AB⊥平面PAB，22224RBDABAD==+,即22243644433R=+

=，∴外接球表面积为643图5ADPO1OCBODO1ABPC2．题设：如图5-1至5-8这七个图形，P的射影是ABC的外心三棱锥ABCP−的三条侧棱相等三棱锥ABCP−的底面ABC在圆锥的底上，顶点P点也是圆锥的顶点.解题步骤：

第一步：确定球心O的位置，取ABC的外心1O，则1,,OOP三点共线；第二步：先算出小圆1O的半径rAO=1，再算出棱锥的高hPO=1（也是圆锥的高）；第三步：勾股定理：21212OOAOOA+=222)(rRhR+−=，解出R方法二：小

圆直径参与构造大圆，用正弦定理求大圆直径得球的直径.图5-1PAO1OCB图5-2PAO1OCB图5-3PAO1OCB图5-4PADO1OCB图5-6DPOO2ABC图5-7POO2ABC图5-8DPOO2AB【外接球模型3】——锥体背景的模型类型六、折叠模型题设：两个

全等三角形或等腰三角形拼在一起，或菱形折叠(如图6)第一步：先画出如图6所示的图形，将BCD画在小圆上，找出BCD和BDA的外心1H和2H；第二步：过1H和2H分别作平面BCD和平面BDA的垂线，两垂线的交点即为球心O，连接OCOE,；第三步：解1OEH，算出1OH，在1OCHRt中

，勾股定理：22121OCCHOH=+注：易知21,,,HEHO四点共面且四点共圆，证略.图6H1EACOBDA'H2类型七、两直角三角形拼接在一起(斜边相同,也可看作矩形沿对角线折起所得三棱锥)模型题设：如图7，90==A

CBAPB，求三棱锥ABCP−外接球半径（分析：取公共的斜边的中点O，连接OCOP,，则ABOPOCOBOA21====，O为三棱锥ABCP−外接球球心，然后在OCP中求出半径），当看作矩形沿对角线折

起所得三棱锥时与折起成的二面角大小无关，只要不是平角球半径都为定值.图7OACBP【多面体的内切球问题模型】类型八、锥体的内切球问题1．题设：如图8-1，三棱锥ABCP−上正三棱锥，求其内切球的半径.第一步：先现出内切球的截面图，HE,分别是两个三角形的外心；第二步：求13DHCD=，rPH

PO−=，PD是侧面ABP的高；第三步：由POE相似于PDH，建立等式：PDPODHOE=，解出r2．题设：如图8-2，四棱锥ABCP−是正四棱锥，求其内切球的半径第一步：先现出内切球的截面图，HOP,,

三点共线；第二步：求BCFH21=，rPHPO−=，PF是侧面PCD的高；第三步：由POG相似于PFH，建立等式：PFPOHFOG=，解出3．题设：三棱锥ABCP−是任意三棱锥，求其的内切球半径方法：等体积法，即内切球球心与四个面构成

的四个三棱锥的体积之和相等第一步：先画出四个表面的面积和整个锥体体积；第二步：设内切球的半径为r，建立等式：PBCOPACOPABOABCOABCPVVVVV−−−−−+++=rSSSSrSrSrSrSVPBCPACPABABCPBCPACPABABCABCP

+++=+++=−)(3131313131第三步：解出PBCOPACOPABOABCOABCPSSSSVr−−−−−+++=3图8-1HDABCPOE图8-2FEHDBACPOG题型一棱柱和圆柱的外接球和内切球1．已知圆柱的底面半径为1，母线长为

2，则该圆柱的外接球的体积为()A．556B．823C．2053D．64232．已知一个长方体的长、宽、高分别为2dm，3dm，32dm，则其外接球的体积为()A．31258dmB．31256dmC．332d

mD．364dm3．已知正方体111ABCDABCD−内切球的表面积为4，则正方体外接球的半径为()A．3B．23C．3D．224．正方体的棱长为2，则它的外接球半径为()A．5B．3C．2D．15．如图，半径为4的球O中有一内接圆柱，当圆柱的侧面积最大时，球的表面积与圆柱的表面积之差为(

)A．64B．48C．32D．166．已知长方体1111ABCDABCD−的长、宽、高分别为2，1，1，且其顶点都在球面上，则该球的体积是()A．6B．6C．36D．867．已知正三棱柱的高与底面边长均为2，则该正三棱柱内半径最大的球与

其外接球的表面积之比为()A．17B．77C．37D．2178．长方体1111ABCDABCD−的底面ABCD为正方形，1AB=，直线1AD与直线1CC所成的角为30，则该长方体外接球的表面积为()A．4B．6C．5D．89．已知正

方体外接球的体积是323，那么此正方体的棱长等于．10．已知圆柱的高为2，侧面积为4，若该圆柱的上、下底面圆周都在某一球的球面上，则该球的体积为．11．已知某圆柱的轴截面是一个正方形，且该圆柱表面积（底面和侧面面积之和）为1

S，其外接球的表面积为2S，则该圆柱的表面积与其外接球的表面积的比值12SS=．12．已知长方体1111ABCDABCD−的体积为325，高为25，则当长方体的表面积最小时，该长方体外接球的体积为．13．某长方体的所有棱长之和为24cm，它的表面积为224cm，则它的

外接球的体积为．题型二棱锥的外接球与内切球14．如图，在四棱锥PABCD−中，已知PA⊥底面ABCD，ABBC⊥，ADCD⊥，且120BAD=，2PAABAD===，则该四棱锥外接球的表面积为()A．8B．20C．205D．

205315．《九章算术》中，将四个面都为直角三角形的四面体称之为鳖臑．在鳖臑PABC−中，PA⊥平面ABC，ABBC⊥，且1PAABBC===，则鳖臑PABC−的外接球的表面积为()A．3B．12C．32D．43

16．在矩形ABCD中23AB=，2AD=，沿对角线BD进行翻折，则三棱锥CABD−外接球的表面积为()A．4B．6C．12D．1617．已知三棱锥ABCD−中，2CD=，1BCACBDAD====，则此

几何体外接球的体积为()A．2B．23C．26D．18．已知三棱锥SABC−中，SA⊥平面ABC，4SA=，23BC=，60BAC=，则三棱锥SABC−外接球的表面积为()A．32B．64C．80D．12819．已知三棱锥PABC−的底面是正三角形，3

AB=，2PA=，PABC⊥，PBAC⊥，PCAB⊥，则三棱锥PABC−的外接球的表面积为()A．43B．32327C．4D．16320．在三棱锥ABCD−中，平面ABD⊥平面BCD，BDCD⊥，且3ABBDDA===，3CD=，则三棱

锥ABCD−的外接球的表面积为()A．154B．15C．32D．621．我国古代数学名著《九章算术》中将底面为矩形且有一侧棱垂直于底面的四棱锥称为“阳马”，现有一“阳马”如图所示，PA⊥平面ABCD，5PA=，3AB=，4BC=，则该“阳马”外接球的表面积为()A．1252

3B．50C．100D．500322．已知三棱锥ABCD−中，底面BCD是边长为23的正三角形，侧面ABD⊥底面BCD，且2ABAD==，则该几何体的外接球的表面积为()A．12B．16C．2

0D．2423．在三棱锥DABC−中，ABC是边长为2的正三角形，ADBD=，23DC=，DC与平面ABC所成的角为60，则三棱锥DABC−的外接球的表面积为()A．509B．1129C．20D．2424．已知三棱锥SABC−中，ABBC⊥，2ABBC==

，22SASC==，二面角BACS−−的大小为23，则三棱锥SABC−的外接球的表面积为()A．1249B．1054C．1059D．104925．已知ABC，3ABAC==，4BC=，将它

沿中线AD折起得四面体ABCD−，使得此时23BC=，则四面体ABCD−的外接球表面积为()A．16B．18C．21D．3626．菱形ABCD中，2AB=，120DAB=，将CBD沿BD折

起，C点变为E点，当四面体EABD−的体积最大时，四面体EABD−的外接球的面积为()A．20B．40C．60D．8027．已知四面体PABC−中，PA⊥平面ABC，2PAAB==，13BC=，且3tan2ABC=，则四面体PABC−的外接球的表面积为()A．15B．17C

．18D．2028．若三棱锥的三条侧棱两两垂直，且三条侧棱长分别为1，2，3，则三棱锥的外接球的表面积是．29．在三棱锥PABC−中，4ABBC==，8PC=，8PA=，ABPA⊥，ABBC⊥，则该三棱

锥外接球的表面积为．30．在正三棱锥SABC−中，6ABBCCA===，点D是SA的中点，若SBCD⊥，则该三棱锥外接球的表面积为．31．在三棱锥DABC−中，已知平面BCD⊥平面ABC，90CBD=，45BCA=，22

AB=，2BD=，则三棱锥ABCD−的外接球的表面积为．32．在平行四边形ABCD中，ABBD⊥，2221ABBD+=，将此平行四边形沿对角线BD折叠，使平面ABD⊥平面CBD，则三棱锥ABCD−外接球的体积是．33．在三棱锥SABC−中，ABC是边长为

2的等边三角形，SAB是以AB为斜边的等腰直角三角形，二面角SABC−−的大小为90，则该三棱锥外接球的表面积为．题型三圆锥的外接球与内切球34．将半径为3圆心角为43的扇形围成一个圆锥，则该圆锥的内切球的体积为()A．16575B．

32575C．165D．3252535．已知底面半径为3的圆锥的侧面积为6，则该圆锥的外接球的体积为()A．323B．43C．12D．1636．已知圆锥的底面半径为1，高为2，该圆锥的顶点和底面圆周上的点都在球O

的表面上，则此球的半径为()A．23B．33C．34D．5437．已知球O在母线长为5，高为4的圆锥内部，则球O的表面积最大值为()A．12B．9C．8D．638．已知圆锥的顶点和底面圆周都在球O面上，圆锥的侧面展开图的圆心角为23，面积为3，

则球O的表面积等于()A．818B．812C．1218D．121239．若球O是圆锥M的内切球，且圆锥M的轴截面是一个边长为2的正三角形，则球O的体积为()A．43B．4327C．439D．4940．如图，已知圆锥PO的底面半径OA的长度为1，母线PA的长度为2，半径为1R的球

1O与圆锥的侧面相切，并与底面相切于点O，则1R=；若球2O与球1O、锥的底面和侧面均相切，则球2O的表面积为．