 DOC
DOC
【文档说明】高中数学人教B版必修4教学教案:3.2.2 半角的正弦、余弦和正切 (2) 含答案.doc,共(4)页,176.000 KB,由envi的店铺上传
转载请保留链接:https://www.doc5u.com/view-83a5100d7df43a79822a20259c93e783.html
以下为本文档部分文字说明:
课题3.2.2半角的正弦、余弦和正切授课教师教学目标1.知识目标:掌握半角的正弦、余弦、正切公式推导方法及结构特点;能正确运用这些公式进行简单三角函数式的化简、求值和证明恒等式。2.能力目标:通过公式的
推导及应用,培养他们的化归思想(换元),分类讨论思想,方程思想和逻辑推理能力。3.德育目标:通过半角公式的推导,以及它们与倍角公式之间的内在联系,培养学生的特殊与一般;相对性;和普遍联系等辨证唯物主义观点。教学重点1.掌握半角的正弦、余弦、正切公式的结构特点,灵活用公式;2.方程思想,
分类讨论思想,和化归思想的运用。教学难点公式前符号的确定;变换中三统一原则的运用;“倍与半”的相对性思考方法。半角与倍角公式之间的内在联系。教学方法本节课运用现代化多媒体教学手段,通过设置问题引导学生观察分析,使学生在独
立思考的基础上进行合作交流,在思考、探索和交流的过程中获得半角公式,对于半角公式的应用采取讲了练结合的方式进行处理,使学生边学边练,及时巩固,同时设计问题,探究问题,深化对公式的记忆。教学环节教学内容师生互动设计意图课题引入气象学
家洛伦兹1963年提出一种观点:南美洲亚马逊河流域热带雨林中的一只蝴蝶,偶尔扇动几下翅膀,可能在两周后引起美国德克萨斯的一场龙卷风。这就是理论界闻名的“蝴蝶效应”,南美洲亚马逊河流域热带雨林中的一只蝴蝶与北美德
克萨斯的龙卷风看来是毫不相干的两种事物,却会有这样的联系,那么“半角与倍角”的三角函数一定会有非常密切的关系!到底是什么关系呢?本节课我们就通过二倍角公式来研究半角的正弦、余弦和正切。课题引入:为引起学生兴趣,拉近师
生距离,我从“倍角与半角关系”入手设置情景引入温故知新复习二倍角的正弦、余弦、正切的公式我们已经学习了二倍角的正弦、余弦、正切的公式请大家回忆一下这组公式的来龙去脉,并请一名同学把这三个公式写在黑板上。温故而知新激活记忆的思维,为推导公
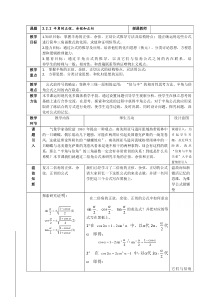
式做铺垫探索研究证明:)3(cos1cos12tan)2(2cos12cos)1(2cos12sin+−=+=−=在二倍角的正弦、余弦、正切的公式中如何求出2tan,2cos,2sin的表达式?并把对应的等式写在黑板上。1在−=2sin212cos中,以
代2,2代即得:2sin21cos2−=∴2cos12sin2−=2在1cos22cos2−=中,以代2,2代即得:它们与倍角公式的推导及理解12cos2cos2−=∴2cos12cos2+=3以上结果相除得:+−=cos1cos
12tan2开方得:)3(cos1cos12tan)2(2cos12cos)1(2cos12sin+−=+=−=然后思考讨论:(投影)这组公式有何特点?应注意些什么?公式有何用处?特点:1左式中的角是右式中的角的一半。2公式的“本质”是用角的余弦表示2角的正
弦、余弦、正切。3根号前均有“”它由角“2”所在象限来确定的,如果没有给定角的范围,“”应保留。注意:公式(3)成立的条件.,2zkk+公式(1)(2)(3)叫做半角公式,实际是二倍角公式的推论。作用:用于三角函数的求值、化
简和证明。由学生回答上述问题,教师点评。公式之间的内在联系通过对三个问题的分析、讨论,使学生对公式有一个清晰完整的认识,为公式的灵活运用打下基础,并给学生一个自由空间,逐步培养他们的自学能力公式的深化对半角公式的“三用”灵活运用公式:1.正用:主要用于
三角函数的求值2.变用:cos122cos12sin222+=−=os(1)正用:次数降低,角增倍。称为降幂公式(2)逆用:次数增高,角减半。称为升幂公式主要用于三角函数的求值、化简和证明对公式进行深挖掘,
培养学生变形能力及化归能力。例1求15tan,15cos,15sin值。巩固练习:求8cot,8cos的值学生练习、板演,教师讲评。分析:(1)对角进行分析发现其二倍角是特殊角30‘其余弦值是已知的。(2)判定三角函
数的符号,因为15是第一象限角,因此都取正号。(3)用半角公使学生进一步熟悉公式特征,为后面的灵活运用作铺垫。公式的应用2例2:已知).23,(,53cos−=,求2tan,2cos,2sin值。变式1:将条件中的“)23,(
”改为“是第三象限角”,结论如何?变式2:将条件中的“)23,(”去掉,结论如何?变式3:将结论改为求“4tan,4cos,4sin”的值。巩固练习已知cos257=,求2tan,
2cos,2sin的值.例3求证:sincos12tan.cos1sin2tan−=+=例4.(1)若322,化简2cos21212121++(2)求式求值即可。教师讲评:(1)运用了化归思想。(2)解题关键:定号。师生共同分析,
学生练习、板演,教师讲评:分析:(1)欲求2的三角函数值,只需已知角的余弦值。(2)由角的范围求2角的范围,再根据2角的所在象限确定符号。(3)用半角公式求值即可。讲评:(1)运用化归思想;(2)基本技巧:使角统一;(3)解题关键是定号。变式1学生回答,教师强调分类讨论思想的运用。变式
2学生回答,教师强调如果没有给定角的范围,“”应保留。师生共同分析,学生练习、板演,教师讲评。分析:(1)已知角和所求角4均与2角具有“倍、半”关系(2)由半角公式求2cos值。(3)再由半
角公式求“4tan,4cos,4sin”的值。教师讲评:角的变换42→→体会“倍、半”关系的相对性。师生共同分析,学生练习、板演,教师讲评。分析:(1)切化弦;(2)分子,分母同乘2sin22cos2或
;(3)逆用二倍角正弦公式和降幂公式即可。或从右式出发,先使用二倍角正弦公式和升幂公式化成半角三角函数,约分后化切即可。教师讲评:(1)降幂公式与升幂公式的应用。(2)三角变换选择公式的依据是:使角统一;名统一;结构统一。(3)运用
化归思想。师生共同分析,学生练习、板演,教师讲评。分析:(1)内层根号提取系数。(2)应用升幂公式。(3)开方即可。及时的小结和升华有利于学生解题技巧的形成。同时起到事半功倍的效果。一般到特殊多角度应用反馈善于对比找出联系拓展变式深
化发展检查学生掌握知识的灵活度让学生掌握一些方便快捷的基本解题方法,使他们在解题时更迅速、准确。此题使学生掌握公式的正用和逆用,有利于启发学生思维,提高学生解题能力;且在解题过程中提炼思想方法,有利于培养学生良好的数学思维品质。这是一道典xxy2sin21cos32+=的最大值、最小值和周期
。巩固练习1.化简:1sincos1sincos+−++2.求证:)4(cos2sin1)4(sin2sin122−=+−=−教师讲评:(1)对结构进行分析。(2)解题关键是开方定号。师生共同分析,学生练习、板演,教师讲评。分析:(1)降幂。(2)合一变形。(3)求最大值、最
小值和周期教师讲评:求三角函数性质问题都要先降幂。后合一变形,化成kxay++=)sin(的形式,方可求解。型例题,对它的接法的深入探讨,有益于启发学生思维,提高学生解题能力。如:变形能力,化归能力和基本解题方法及常用的思维策略。课堂总
结与升华从知识、方法两个方面来对本节课内容进行归纳小结。1.记忆今天所学习的半角公式,注意公式的结构,尤其是符号的选择。2.注意公式的定义域,及公式的三用。3.三角变换过程中常用的思维策略的:三“统一”即角统一;名统一;结构统一。4.注意化归转化思想、方程思想与分类讨论思想的运用。4)化简
要求及证明途径。使学生对所学内容有一个清晰完整的认识,指出学习三角公式的基本方法,体现了“授之以渔,而不是授之以鱼”的教育思想。布置作业作业:P146练习A1.2.3.练习B1.2.3.课后思考题:求22sincossin32cosxxxxy−−=的值
域、单调性周期性并判断其奇偶性。巩固本节所学知识,同时给学有余力的同学留出自由发展的空间。