【文档说明】专题01 领悟八项技能，深刻掌握平行线知识讲义（原卷版）.docx，共(31)页，1.056 MB，由管理员店铺上传

转载请保留链接：https://www.doc5u.com/view-54ad036db3e82c8aeb46448d6f1637fd.html

以下为本文档部分文字说明：

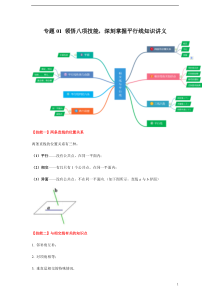
1专题01领悟八项技能，深刻掌握平行线知识讲义【技能一】两条直线的位置关系两条直线的位置关系有三种：（1）平行——没有公共点，在同一平面内；（2）相交——有且只有1个公共点，在同一平面内；（3）异面——没有公共点，不在同一平面内.（如下图所示，直线a与b异面）

【技能二】与相交线有关的知识点1.邻补角互补；2.对顶角相等；3.垂直是相交的特殊情况.2判断两直线垂直的方法：两直线相交形成的四个角中，①一个为直角；②邻补角相等；③对顶角互补.4.垂线段最短；5.从直线外一点到直线的垂线段的长

度，叫做点到直线的距离.6.直角三角形斜边上的高等于直角边的乘积除以斜边的长.由S△=ab÷2=ch÷2得：h=ab÷c【技能三】三线八角被截线截线结构特征同位角同一方同旁F内错角之间两旁Z同旁内角之间

同旁U1.同位角近似“F”【★同位角不一定相等】2.内错角近似“Z”【★内错角不一定相等】33.同旁内角近似“U”【★同旁内角不一定互补】【技能四】平行线的知识点同一平面内，永远不相交的两条直线互相平行，直线a与直线b平行，记作a∥b.【技能五】令人“烦恼”的前提前提

：“同一平面内”，“直线外”在哪些情况下添加？过直线外一点，有且只有一条直线与已知直线平行；同一平面内，过一点有且只有一条直线与已知直线垂直；同一平面内，同垂直于一条直线的两条直线互相平行；【技能六】平行线的判定六法1.定义——同一平

面内，不相交的两条直线平行2.同位角相等，两直线平行3.内错角相等，两直线平行4.同旁内角互补，两直线平行5.平行线传递性6.同一平面内，同垂直于一条直线的两条直线互相平行4【技能七】平行线的性质及命题两直线平行，同位角

相等，内错角相等，同旁内角互补.命题组成：题设、结论.形式：如果……，那么……分类：真命题，假命题★若两个角的两组边分别平行（垂直），则这两个角相等或互补.【如下图所示】【技能八】平移性质两条线段平移前后，长度不变，位置共线或平行.考点一：相

交线题型一、基本概念例1．（2020·江阴市长泾月考）下列说法错误的是（）A．对顶角相等B．两点之间所有连线中，线段最短C．等角的补角相等D．过任意一点P，只能画一条直线5【变式1－1】（2020·右玉

县期中）下列说法中正确的有（）①对顶角相等；②一个角的补角大于这个角；③互为邻补角的两个角的平分线互相垂直；④若两个实数的和是正数，则这两个实数都是正数．A．1个B．2个C．3个D．4个题型二、求角度例2－1．（2021·江西赣州期末）北京大兴国际机场采用“三纵一横”全

向型跑道构型，可节省飞机飞行时间，過极端天气侧向跑道可提升机场运行能力．跑道的布局为：三条南北向的跑道和一条偏东南走向的侧向跑道．如图，侧向跑道AB在点O南偏东70°的方向上，则这条跑道所在射线OB与正北方向所成角的度数为（）A．160°B．110°C．70°D．20°例2－2．（202

0·浙江嘉兴期末）将一把直尺和一块三角板如图叠放，直尺的一边刚好经过直角三角板的直角顶点且与斜边相交，则1与2一定满足的数量关系是（）6A．221=B．21180+=C．221180+=D．2190−=【变式2－1】．（2021·山

东济南期中）如图，直线m和n相交于点O，若∠1=40°，则∠2的度数是（）A．40°B．50°C．140°D．150°【变式2－2】．（2019·河北邢台期末）小明用一副三角板自制对顶角的“小仪器”，第一步固定直角三角板ABC，并将边AC延长至点P，第二步将另一块三角板CDE的直角顶点与三角

板ABC的直角顶点C重合，摆放成如图所示，延长DC至点F，PCD与ACF就是一组对顶角，若30ACF=，则PCD=__________，若重叠所成的∠BCE=n°（0＜n＜90），则∠PCF的度数为__________．7【变式2－3】（2020·广东阳江期末）如图，两条直线AB，

CD交于点O，射线OM是∠AOC的平分线，若∠BOD＝80°，则∠BOM的度数是．题型三、综合题例3.（2021·湖北十堰期末）如图，直线AB，CD相交于点O，OE平分∠AOD，OF⊥OC，（1）图中∠

AOF的余角是________(把符合条件的角都填出来)；（2）如果∠AOC=140°，那么根据________，可得∠BOD=________；（3）如果∠1=31°，求∠2和∠3的度数．8【变式3－1】（2021·辽宁抚顺期末）如图，已知O为直线AD上一点

，OB是AOC内部一条射线且满足AOB与AOC互补，OM，ON分别为AOC，AOB的平分线．（1）COD与AOB相等吗？请说明理由；（2）若30AOB=，试求MON的度数；（3）若MON=，请直接写出AOC的度数．

（用含α的式子表示）考点二：垂线题型一、基础概念例1－1.（2021·山东临沂期末）下列四个生活、生产现象：①用两枚钉子就可以把木条固定在墙上；②植树时，只要定出两棵树的位置，就能确定同一行树所在的直线；③体育课上，老师测量某同学的跳远成绩；④把弯曲的公路改直，就能缩短路程

，其中可用基本事实“两点确定一条直线”来解释的现象有（）A．①②B．①③C．②④D．③④例1－2．（2021·北京顺义期末）如图，点P在直线l外，点A、B在直线l上，若4PA=，7PB=，则点P到直线l的距离可能是（）A．3B．4C．5D．79例1－3．（

2020·湖南湘潭月考）下列命题中，其中正确的有（）．①两条相交直线组成的四个角相等，则这两直线垂直．②两条相交直线组成的四个角中，若有一个直角，则四角都相等．③两条直线相交，一角的两邻补角相等，则这两直线垂直．④两条直线相交

，一角与其邻补角相等，则这两直线垂直．A．1个B．2个C．3个D．4个【变式1－1】（2019·山西月考）如图，在三角形ABC中，90ACB=，CDAB⊥于点D，则图中能表示点B到直线AC的距离的是（）A．CD的长度B．BC的长度C．BD的长度D．AD的长度【变式1－2】

（2020·福建三明期中）如图所示，某工程队计划把河水引到水池A中，他们先过A点作ABCD⊥，垂足为B，然后沿AB开渠，可以节约人力、物力和财力，这样设计的数学依据是（）A．两点之间线段最短B．经过两点有且

只有一条直线C．垂直定义D．垂线段最短10【变式1－3】（2020·广西贺州期末）下列语句错误．．的是（）．A．直线外一点到这条直线的垂线段叫做点到直线的距离．B．在直线外一点与直线上各点的线段中，垂线段最短．C．同一平面内，过一点有且只有一条直线垂直于已知直线．D．经过直线外一点，有且只有一

条直线平行于这条直线．题型二、相关计算例2－1.（2020·河南省淮滨县第一中学七年级期末）如图，OAOC⊥，OBOD⊥，且150AOD=，则BOC的度数是（）A．60B．30°C．50D．

40例2－2．（2019·浙江杭州）已知60BOC=，OF平分BOC．若AOBO⊥，OE平分AOC，则EOF的度数是（）11A．45B．15C．30或60D．45或15例2－3．（2021·江苏泰州期末）如图，直线AB、CD相交于点O，OE

平分∠BOD，OF⊥CD，若∠BOC比∠DOE大75o．求∠AOD和∠EOF的度数．【变式2－1】（2019·四川绵阳期末）如图，若直线AB与CD相交于点O，OD平分BOF，OEOF⊥且29BOD=，则CO

E的度数为（）A．116B．118C．119D．120【变式2－2】（2020·湖北咸宁期末）如图，直线AB、CD相交于点O，OE平分∠AOC，OF⊥OE于点O，若∠AOD＝70°，则∠AOF＝__

____度．12【变式2－3】（2020·沭阳县月考）已知如图，直线AB、CD相交于点O，∠COE=90°．（1）若∠AOC=36°，求∠BOE的度数；（2）若∠BOD：∠BOC=1：5，求∠AOE的度数；（3）在（2）的条件下，过点O作OF⊥AB，请直接写出∠EOF的度数．【变式2－4】如

图，直线BC、DE相交于点O，OA、OF为射线，OAOB⊥，OF平分BOE，BOFCOD+＝54．求AOE的度数．13考点三：三线八角例1.（2020·长汀县月考）如图所示，下列结论中正确的是（）A．∠1和∠2是同位角B．∠1和∠4是内错角C．∠2和∠

3是同旁内角D．∠3和∠4是对顶角例2．（2019·商水县期末）如图所示，同位角有a对，内错角有b对，同旁内角有c对，则a+b－c的值是____________例3．（2021·河南周口期末）如图，找出

标注角中的同位角、内错角和同旁内角．14【变式1】．（2020·黑龙江哈尔滨期末）如图，1和2不是同旁内角的是（）A．B．C．D．【变式2】．（2019·河南洛阳期中）如图，1和2是同位角的有（）A．①②B．①③C．②③D．②④【变式3】．（2020·河南周口期中）

如图，直线AB，CD被直线EF所截，与AB，CD分别交15于点E，F，下列描述：①∠1和∠2互为同位角②∠3和∠4互为内错角③∠1=∠4④∠4+∠5=180°其中，正确的是（）A．①③B．②④C．②③D．③④【变式4】（2020·湖北武汉月考

）如图所示的图形中，同位角有_____对考点四：平行线例1.（2021·江苏宿迁期末）下列说法错误的是（）A．平面内过一点有且只有一条直线与已知直线平行B．平面内过一点有且只有一条直线与已知直线垂直C．两点之间的所有连线中，线段最短

D．对顶角相等16例2．（2020·四川师范大学附属中学期中）下列说法中不正确的个数为（）．①在同一平面内，两条直线的位置关系只有两种：相交和垂直．②有且只有一条直线垂直于已知直线．③如果两条直线都与第三条直线平行，那么这两条直线也互相平行．④从直线外一点到这条直线的垂线段，叫做这点到这条直线

的距离．⑤过一点，有且只有一条直线与已知直线平行．A．2个B．3个C．4个D．5个【变式1】．（2021·陕西宝鸡期末）下列说法中正确的个数为（）①不相交的两条直线叫做平行线；②平面内，过一点有且只有一条直线与已知直线垂直；③平行于同一条直线的两条直线互相平行；④在同一平面内，两条直线不是平行就

是相交．A．1个B．2个C．3个D．4个【变式2】．（2020·江苏苏州期中）下列说法中：①对顶角相等；②同位角相等；③平行于同一条直线的两条直线平行；④垂直于同一条直线的两条直线垂直；其中正确的有（）A．1个B．2个C．3个D．4个

【变式3】．（2019·山西月考）已知AOB内部有一点M，过点M画OA的平行线，这样17的直线（）A．有且只有一条B．有两条C．有三条D．有无数条考点五：平行线的判定例1.（2020·浙江杭州期中）如图，下列四个图中12=，不能判断不能判

定//ab的是（）A．B．C．D．例2．（2021·河南开封期末）如图，下列条件能判断//ADCB的是（）A．180DDAB+=B．12=C．34=D．45=18例3．（2021·福建三明期末）如图是利用直

尺和三角板过直线l外一点P作直线l的平行线的方法，这样做的依据是（）A．同位角相等，两直线平行B．两直线平行，同位角相等C．两直线平行，内错角相等D．内错角相等，两直线平行例4．（2021·浙江绍兴期末）如

图，已知CD⊥DA，DA⊥AB，∠1=∠4．试说明DF∥AE．请你完成下列填空，把证明过程补充完整．证明：∵_________（___________）∴∠CDA=90°，∠DAB=90°（_________）．∴∠4+∠3=90°，∠2+∠1=90°．又∵∠1=∠4，∴_____（___

__），∴DF∥AE（______）．19例5．（2020·甘肃张掖期末）已知：如图，1C=，2和D互余，1和D互余，求证：//ABCD．例6．（2020·渠县月考）已知：如图，,,,ACABBDABCAEDBF⊥⊥=且请猜

想直线AE与BF的位置关系，并说明理由．【变式1】（2020·洛阳市月考）下面是投影屏上出示的抢答题，需要回答横线上符号代表的内容，则回答正确的是（）已知：如图，∠BEC＝∠B+∠C，求证：AB∥CD

证明：延长BE交__※__于点F，则∠BEC＝__⊙__+∠C20又∵∠BEC＝∠B+∠C，∴∠B＝▲∴AB∥CD（__□__相等，两直线平行）A．⊙代表∠FECB．□代表同位角C．▲代表∠EFCD．※代表AB【变式2】（2020·浙

江金华期末）下列说法中：（1）不相交的两条直线叫做平行线；（2）经过一点，有且只有一条直线与已知直线平行；（3）垂直于同一条直线的两直线平行；（4）直线//ab，//bc，则//ac；（5）两条直线被第三条直线所截，同位角相等．其中正确的是__

______．【变式3】（2019·山西期末）如图1，在探索“如何过直线外一点作已知直线的平行线”时，小颖利用两块完全相同的三角尺进行如下操作：如图2所示，（1）用第一块三角尺的一条边贴住直线l，第二块三角尺的一条边紧靠第一块三角

尺；（2）将第二块三角尺沿第一块三角尺移动，使其另一边经过点A，沿这边作出直线AB，直线AB即为所求，则小颖的作图依据是________．21【变式4】（2020·江西宜春期末）如图，已知点E在直线DC上，射线EF平分∠AED，过E点作EB⊥EF，G为射线EC上一点，连结B

G，且90EBGBEG+=．（1）求证：DEFEBG=；（2）若EBGA=，试判断AB与EF的位置关系，并说明理由．考点六：平行线的性质题型一、求度数例1－1.（2020·浙江杭州期中）如图，//ABCD，ADAC⊥，32ADC=，则CAB的度数

是（）22A．120度B．121度C．122度D．123度例1－2．（2021·山东潍坊期末）一把直尺与30°的直角三角板如图所示，150=，则2=（）A．50°B．60°C．70°D．80°【变式1－1】（2020·浙江金华期中）如图所示，已知AD与BC相交于点O，////

CDOEAB．如果40B=，30D=，则AOC的大小为（）A．60°B．70°C．80°D．120°23【变式1－2】如图，∠1＝∠2，AC平分∠DAB，且∠D：∠DAB＝2：1，则∠D的度数是（）A．120°B．130°C．140°D．150°题型二、方位角例2.（2021·甘

肃白银期末）一条船停留在海面上，从船上看灯塔位于北偏东60°方向，那么从灯塔看船位于灯塔的方向（）A．南偏西60°B．西偏南60°C．南偏西30°D．北偏西30°【变式】如图，李强和同事驾驶快艇执行巡逻任务，他们从岛屿A处向正

南方向航行到B处时，向右转60航行到C处，再向左转80继续航行，此时快艇的航行方向为（）A．南偏东20B．南偏东80C．南偏西20D．南偏西80题型三、综合题型例3－1.（2020·浙江杭州期中）已知A的两边与BÐ的两边分别平行，若A

的度数比BÐ的2倍少30°，则BÐ的度数是（）24A．30°B．50°C．30°或70°D．50°或70°例3－2．如图，已知直线AB、CD被直线AC所截，//ABCD，E是直线AC右边任意一点（点E不在直线AB，

CD上），设BAE=，DCE=．下列各式：①+，②−，③−，④360−−，AEC的度数可能是（）A．①②③B．①②④C．①③④D．①②③④25例3－3．（2021·陕西咸阳期末）如

图，360ABCCCDE++=，直线FG分别交AB、DE于点F、G．若1110=，则2=___________．例3－4．（2021·陕西西安期末）如图，178=，2102=，CD=．求证：//ACDF．【变式3－1】（2021·山东青岛期末）如图，

//ABCD，点E在AC上，110A=，15D=，则下列结论正确的个数是（）（1）AEEC=；（2）85AED=；（3）ACEDD=+；（4）45BED=A．1个B．2个C．3个D．4个26【变式3－2】（202

1·广西贵港期末）如图，直线a，b，//ab，点C在直线b上，90DCB=，若170=，则2的度数为______．【变式3－3】（2020·浙江金华期中）已知A与BÐ（A，BÐ都是大于0°

且小于180°的角）的两边一边平行，另一边垂直，且227AB−=，则A的度数为_________．【变式3－4】（2020·黑龙江哈尔滨期末）在同一平面内，A与BÐ的两边分别平行，若50A=，则BÐ的度数为_

_________．27【变式3－5】（2021·河南洛阳期末）直线AB和CD被直线MN所截，如图1，EG平分MEB，FH平分DFE，当12=时，小明证明//ABCD的过程如下：∵EG平分MEB，FH平分DFE（已知），∴21MEB=，22DFE=（角平分线的定

义）．∵12=，（已知），∴MEBDFE=（等量代换）．∴//ABCD（同位角相等，两直线平行）．请你参考上述证明过程解决下列问题：（1）如图2，EG平分AEF，FH平分DFE，1与2满足什么条件时，//ABCD？说明理由．（2）如图3，若//ABC

D，EG平分AEM，FH平分CFN，则1与2满足怎样的条件？说明理由．28【变式3－6】（2021·四川成都期末）完成下面推理过程，在括号内的横线上填空或填上推理依据．如图，已知：//ABEF,EPEQ⊥，90EQCAPE

+=，求证：//ABCD29证明：//ABEFAPE=__________（__________）EPEQ⊥PEQ=_________（___________）即90QEFPEF+=90APEQEF+=90EQCAPE+=

EQC=________//EF_______（__________________）//ABCD（________________）考点七：命题例1.举反例说明“互为补角的两个角都是直角”为假命题．例2．（2021·浙江绍兴期末）把“同位角相等”写成“如果…那么…

”的形式为：为_____．30【变式1】判断下列命题的真假，如果是假命题，请举一个反例，真命题不需要举例．（1）钝角的补角是锐角；（2）一个角的余角小于这个角；（3）如果ab=，那么ab=．【变式2】（2021·山东青岛期末）把命题“锐角小于90°”

改写成“如果……那么……”的形式：______．考点八：平移例1.（2020·浙江杭州模拟）如图，将ABC沿AC方向平移1cm得到DEF，若ABC的周长为10cm，则四边形ABEF的周长为（）A．14cmB．13cmC．1

2cmD．10cm例2．（2021·上海宝山期末）如图，ABC经过平移后得到DEF，下列说法：①//ABDE31②ADBE=③ACBDFE=④ABC和DEF的面积相等⑤四边形ACFD和四边形BCFE的面枳相等，其中正确的有（）A．4个B．3

个C．2个D．1个【变式1】（2021·北京丰台期末）如图，将ABC沿BC所在的直线平移得到DEF．如果2GC=，4.5DF=，那么AG=____．【变式2】（2021·上海浦东新区期末）如图，已知直角三角形ABC，90A=，4AB=厘米，3AC=厘米，5BC=厘米，将ABC沿AC方向

平移1.5厘米，线段BC在平移过程中所形成图形的面积为__________平方厘米．